1.3: No Tan Apretado

De hecho, hay aproximaciones ocultas en el análisis anterior, por un lado, hemos asumido que la longitud de la cadena entre\(\begin{equation}x \text { and } x+d x \text { is } d x\end{equation}\), pero realmente es ds, donde el parámetro de distancia s se mide a lo largo de la cadena. Segundo, tomamos la tensión para ser invariable. Esa es una aproximación bastante buena para una cuerda que es casi horizontal, pero piensa en una cuerda de un metro de largo colgando entre dos puntos separados a 5 cm, y se hace evidente que ambas aproximaciones solo son buenas para una cuerda casi horizontal.

Obviamente, con la cuerda casi vertical, la tensión está equilibrando el peso de la cuerda debajo de ella, y debe estar cerca de cero en la parte inferior, aumentando aproximadamente linealmente con la altura. Por no mencionar, está claro que esto no es parábola, los dos lados están muy cerca de paralelos cerca de la cima. Evidentemente,\(\begin{equation}T\end{equation}\) la aproximación constante no es buena, pero Whewell resolvió este problema exactamente, allá por la década de 1830.

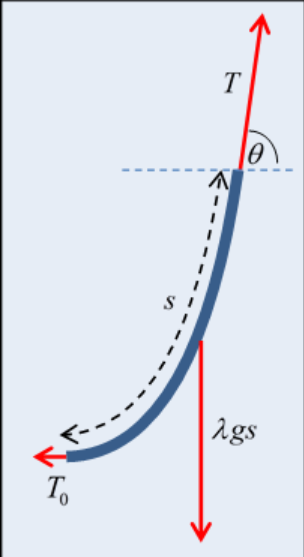
Lo que hizo fue trabajar con la ecuación de equilibrio estático para una longitud finita de cuerda, un extremo en la parte inferior.

Si la tensión en la parte inferior es\(\begin{equation}T_{0}\end{equation}\) y a una distancia s de distancia, medida a lo largo de la cuerda, la tensión es\(T\), y el ángulo de la cuerda con la horizontal hay\(\theta\) (ver diagrama), entonces el equilibrio de equilibrio de los componentes de fuerza es

\ begin {ecuación} T\ cos\ theta=t_ {0},\ quad T\ sin\ theta=\ lambda g s\ final {ecuación}

a partir del cual la pendiente de la cuerda

\ begin {ecuación}\ tan\ theta=\ frac {\ lambda g} {T_ {0}} s=\ frac {s} {a}\ end {ecuación}

donde hemos introducido la constante\(\begin{equation}a=T_{0} / \lambda g\end{equation}\), que establece la escala de longitud del problema.

Entonces ahora tenemos una ecuación para la catenaria,\(\theta\) en términos de s, distancia a lo largo de la cadena. Lo que queremos, aunque es una ecuación para la posición vertical\(y\) en términos de posición horizontal\(x\), la función\(\begin{equation}y(x)\end{equation}\) para la cadena.

Ahora hemos demostrado que la pendiente es

\ begin {ecuación} d y/d x=\ tan\ theta=s/a\ end {ecuación}

y los infinitesimales están relacionados por\(\begin{equation}d s^{2}=d x^{2}+d y^{2}\end{equation}\), así que juntando estas ecuaciones

\ begin {ecuación}\ izquierda (\ frac {s} {a}\ derecha) ^ {2} =\ izquierda (\ frac {d y} {d x}\ derecha) ^ {2} =\ izquierda (\ frac {d s} {d s} {d x}\ derecha) ^ {2} -1\ end {ecuación}

es decir,

\ begin {ecuación}\ izquierda (\ frac {d s} {d x}\ derecha) ^ {2} =1+\ izquierda (\ frac {s} {a}\ derecha) ^ {2} =\ frac {a^ {2} +s^ {2}} {a^ {2}}\ end {ecuación}

Tomando la raíz cuadrada y reordenando

\ begin {ecuación}\ frac {d s} {\ sqrt {a^ {2} +s^ {2}}} =\ frac {d x} {a}\ end {ecuación}

que se puede integrar inmediatamente con la sustitución

\ begin {ecuación} s=a\ sinh\ xi,\ quad d s=a\ cosh\ xi d\ xi\ fin {ecuación}

para dar solo

\ begin {ecuación} d\ xi=d x/a\ end {ecuación}

que se integre trivialmente a\(\begin{equation}\xi=(x / a)+b, \text { with } b\end{equation}\) una constante de integración, o

\ begin {ecuación} s=a\ sinh\ xi=a\ sinh (x/a)\ fin {ecuación}

elegir el origen\(\begin{equation}x=0 \text { at } s=0, \text { which makes } b=0\end{equation}\)

Pero claro lo que queremos es la forma de la curva\(\begin{equation}y(x), \text { not } s(x)\end{equation}\). Tenemos que eliminar\(s\) a favor de\(y\). Es decir, tenemos que escribir\(y\) en función de\(s\), luego sustituir\(\begin{equation}s=a \sinh (x / a)\end{equation}\)

Recordemos que una de nuestras primeras ecuaciones fue para la pendiente\(\begin{equation}d y / d x=s / a\end{equation}\), y armando eso con\(\begin{equation}s=a \sinh (x / a)\end{equation}\) da

\ begin {ecuación} a d y=s d x=a\ sinh (x/a) d x\ end {ecuación}

integrando a

\ begin {ecuación} y=a\ cosh (x/a)\ end {ecuación}

Esta es la ecuación deseada para la curva catenaria\(\begin{equation}y(x)\end{equation}\)

Hemos bajado la posible constante de integración, que es solo el posicionamiento vertical del origen.

Pregunta: ¿es esto lo mismo que la curva de la cadena en un puente colgante?

(Observe que los cables verticales están uniformemente espaciados horizontalmente.)