8.1: Función de la posición de punto final

Ahora pensaremos en variar la acción de una manera ligeramente diferente. (Nota: Estamos usando la notación de Landau.) Anteriormente, consideramos la integral del Lagrangiano sobre todos los caminos diferentes posibles desde el lugar inicial y el tiempo\ (\ begin {ecuación}
q^ {(1)}, t_ {1}
\ end {ecuación}\) hasta el lugar y tiempo final\ (\ begin {ecuación}
q^ {(2)}, t_ {2}
\ end {ecuación}\)

y encontró el camino de acción mínima. Ahora, sin embargo, comenzaremos con esa ruta, la ruta física real, e investigaremos la acción correspondiente en función de las variables finales del punto final, dado un lugar y una hora de inicio fijos.

Tomando un grado de libertad (la generalización es sencilla), para una pequeña variación de camino el cambio incremental en la acción

\ begin {ecuación}
\ delta S=\ izquierda [\ frac {\ parcial L} {\ parcial\ punto {q}}\ delta q\ derecha] _ {t_ {1}} ^ {t_ {2}} +\ int_ {t_ {1}} ^ {t_ {2}}\ izquierda (\ frac {\ parcial L} {\ parcial q} -\ frac {d} d t}\ frac {\ parcial L} {\ parcial\ punto {q}}\ derecha)\ delta q d t
\ final {ecuación}

(Recordemos que el primer término proviene del cálculo de variaciones cuando permitimos que el punto final varíe — es exactamente el mismo punto que discutimos anteriormente en el problema de la brachistocrona del tiempo más rápido para una distancia horizontal dada, permitiendo que la posición vertical del punto final sea un parámetro libre.)

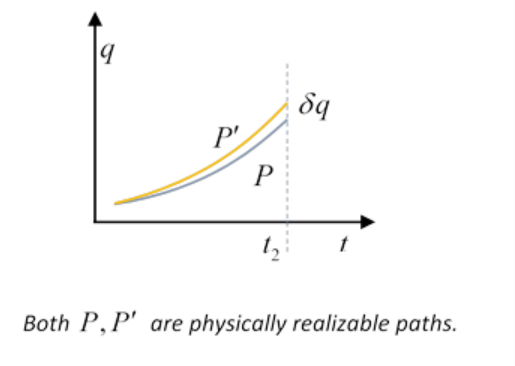
Con la variación incremental, hemos pasado de la ruta física P (seguida del sistema en el espacio de configuración de\ (\ begin {ecuación}
q^ {(1)}, t_ {1}\ text {a}\ left.q^ {(2)}, t_ {2}\ right)
\ end {ecuación}\) a una segunda ruta\ (\ begin {ecuación}
P^ {\ prime}
\ end {ecuación}\) comenzando en el mismo lugar y tiempo, y terminando al mismo tiempo\ (\ begin {ecuación}
t_ {2}
\ end {ecuación}\) como P, pero en un lugar ligeramente diferente\ (\ begin {ecuación}
q^ {(2)} +\ delta q\ left (t_ {2}\ right)
\ end {ecuación}\).

Ambas rutas\ (\ begin {ecuación}
P, P^ {\ prime}
\ end {ecuación}\) están completamente determinadas por sus posiciones y tiempos iniciales y finales, así que\ (\ begin {ecuación}
P, P^ {\ prime}
\ end {ecuación}\) deben corresponder a velocidades iniciales ligeramente diferentes. El punto importante es que dado que ambos caminos describen el desarrollo dinámico natural del sistema a partir de las condiciones iniciales, el sistema obedece las ecuaciones de movimiento en todo momento a lo largo de ambos caminos, y por lo tanto el término integral en la ecuación anterior es idénticamente cero.

Escribiendo\ (\ begin {ecuación}
\ delta q\ left (t_ {2}\ right) =\ delta q, p^ {(2)} =p
\ end {ecuación}\) la acción, considerada como una función de la variable de posición final, con el tiempo final fijado en\ (\ begin {ecuación}
t_ {2}
\ end {ecuación}\), tiene la diferencial

\ begin {ecuación}
\ delta S\ izquierda (q^ {(2)}, t_ {2}\ derecha) =\ izquierda [\ frac {\ parcial L} {\ parcial\ punto {q}}\ delta q\ derecha] _ {t_ {1}} ^ {t_ {2}} =p^ {(2)}\ delta q^ {(2)} =p\ delta q
final {ecuación}

Para el caso multidimensional, el cambio incremental en la acción al variar la variable de posición final viene dado por (dejando caer el superíndice)

\ begin {ecuación}
\ parcial S/\ parcial q_ {i} =p_ {i}
\ final {ecuación}