16.4: Analizando Dispersión Repulsiva de Cuadratura Inversa- Kepler Nuevamente

Para avanzar más, debemos calcular\(b(\chi)\), o equivalentemente\(\chi(b)\): ¿cuál es el ángulo de dispersión, el ángulo entre la velocidad de salida y la velocidad entrante, para un parámetro de impacto dado? \(\chi\)por supuesto también dependerá de la fuerza de la repulsión, y de la energía entrante de las partículas.

Recordemos nuestra ecuación para las órbitas de Kepler:

\ begin {ecuación}\ frac {d^ {2} u} {d\ theta^ {2}} +u=\ frac {G M m^ {2}} {L^ {2}}\ end {ecuación}

Pasemos ahora de la dispersión gravitacional con una fuerza atractiva\(G M m / r^{2}\) a una fuerza repulsiva eléctrica entre dos cargas\(Z_{1} e, Z_{2} e\), fuerza fuerza\(\frac{1}{4 \pi \varepsilon_{0}} \frac{Z_{1} Z_{2} e^{2}}{r^{2}}=\frac{k}{r^{2}}\), digamos. Como esto es repulsivo, el signo cambiará en la ecuación de aceleración radial,

\ begin {ecuación}\ frac {d^ {2} u} {d\ theta^ {2}} +u=-\ frac {k m} {L^ {2}}\ end {ecuación}

Además, queremos que la dispersión sea parametrizada en términos del parámetro de impacto b y la velocidad entrante\(v_{\infty}\), así que poner\(L=m v_{\infty} b\) esto es

\ begin {ecuación}\ frac {d^ {2} u} {d\ theta^ {2}} +u=-\ frac {k} {m b^ {2} v_ {\ infty} ^ {2}}\ end {ecuación}

Así como con el problema de Kepler, la órbita viene dada por

\ begin {ecuación}\ frac {1} {r} =u=-\ frac {k} {m b^ {2} v_ {\ infty} ^ {2}} +C\ cos\ izquierda (\ theta-\ theta_ {0}\ derecha) =-\ kappa+C\ cos\ izquierda (\ theta-\ theta_ {0}\ derecha),\ texto {decir.}\ final {ecuación}

De la conferencia sobre Matemáticas Orbitales, la ecuación polar para la rama hipérbola izquierda relativa al foco externo (derecho) es

\ begin {ecuación}\ mathrm {l}/r=-e\ cos\ theta-1\ end {ecuación}

esta es una rama simétrica alrededor del\(x\) eje -eje:

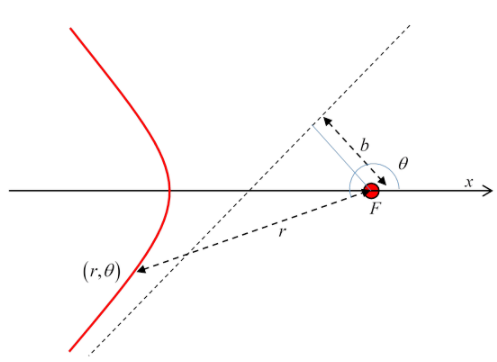
Pero queremos que la rama entrante sea paralela al eje, lo que hacemos por elección adecuada de\(\theta_{0}\). En otras palabras, giramos la hipérbola en el sentido de las agujas del reloj a través de la mitad del ángulo entre sus asíntotas, manteniendo fijo el centro de dispersión (enfoque de la derecha).

De la conferencia sobre matemáticas orbitales (última página), la distancia perpendicular del foco a la asíntota es el parámetro hipérbola\(b!\). Presumiblemente, esta es la razón por la que usamos\(b\) para el parámetro de impacto. De ahí que la partícula vaya en una ruta hiperbólica con parámetros\(e / \mathrm{l}=-C, \quad 1 / \mathrm{l}=\kappa\). Esta no es suficiente información para fijar el camino de manera única: solo hemos alimentado en el momento angular\(m b v_{\infty}\) no la energía, por lo que esta es una familia de caminos que tienen diferentes parámetros de impacto pero el mismo momento angular.

Podemos, sin embargo, fijar el camino de manera única equiparando la corrección de orden inicial con la trayectoria recta de orden cero entrante: la partícula viene en paralelo al\(x\) eje -lejos a la izquierda, distancia perpendicular\(b\) del eje, es decir, de la línea\(\theta=\pi\). Entonces, volviendo a ese tiempo de pre-dispersión,

\ begin {ecuación} u\ fila derecha 0,\ quad\ pi-\ theta\ fila derecha b/r=b u\ end {ecuación}

y en este pequeño\(u\) límite,

\ begin {ecuación} u=C\ cos\ izquierda (\ pi-b u-\ theta_ {0}\ derecha) -\ kappa\ cong C\ cos\ izquierda (\ pi-\ theta_ {0}\ derecha) -\ kappa+b C u\ sin\ izquierda (\ pi-\ theta_ {0}\ derecha)\ end {ecuación}

Coincidencia del orden cero y los términos del primer orden

\ begin {ecuación} C\ cos\ izquierda (\ pi-\ theta_ {0}\ derecha) =\ kappa,\ quad u=b C u\ sin\ izquierda (\ pi-\ theta_ {0}\ derecha)\ final {ecuación}

elimina\(C\) y fija el ángulo\(\theta_{0}\), que es el ángulo por el que se tuvo que girar la hipérbola para alinear la asíntota con el\(x\) eje negativo, y por lo tanto la mitad del ángulo entre las asíntotas, que sería\(\pi\) menos el ángulo de dispersión\(\chi\) (ver el anterior diagrama),

\ begin {ecuación}\ tan\ izquierda (\ pi-\ theta_ {0}\ derecha) =-\ tan\ theta_ {0} =\ frac {1} {b\ kappa} =\ frac {m b v_ {\ infty} ^ {2}} {k}\ end {ecuación}

\ begin {ecuación}\ chi=\ pi-2\ cot ^ {-1} b\ kappa=2\ tan ^ {-1} b\ kappa\ fin {ecuación}

Entonces este es el ángulo de dispersión en términos del parámetro de impacto\(b\), es decir, en el diagrama anterior

\ begin {ecuación}\ chi (b) =2\ tan ^ {-1}\ izquierda (\ frac {k} {m b v_ {\ infty} ^ {2}}\ derecha)\ end {ecuación}

Equivalentemente,

\ begin {ecuación}
b=\ frac {k} {m v_ {\ infty} ^ {2}}\ cuna\ frac {\ chi} {2},\ texto {so} d b=\ frac {k} {2 m v_ {\ infty} ^ {2}}\ nombre del operador {cósec} ^ {2}\ frac {\ chi} {2} d chi\
\ end {ecuación}

y el área de sección transversal incremental

\ begin {ecuación}
d\ sigma=2\ pi b d b=\ pi\ izquierda (\ frac {k} {m v_ {\ infty} ^ {2}}\ derecha) ^ {2}\ nombreoperador {cósec} ^ {2}\ frac {1} {2}\ chi\ cot\ frac {1} {2}\ chi d\ chi=\ pi\ izquierda (\ frac {k} {m v_ {\ infty} ^ {2}}\ derecha) ^ {2}\ frac {\ cos\ frac {1} {2}\ chi} {\ sin ^ {3}\ frac {1} {2}\ chi} d\ chi=\ izquierda (\ frac {k} {2 m v_ {\ infty} ^ {2 }}\ derecha) ^ {2}\ frac {1} {\ sin ^ {4}\ frac {1} {2}\ chi} d\ Omega
\ fin {ecuación}

Esta es la fórmula de Rutherford: la sección transversal incremental para la dispersión en un ángulo sólido incremental, la sección transversal diferencial

\ begin {ecuación}
\ frac {d\ sigma} {d\ Omega} =\ izquierda (\ frac {k} {2 m v_ {\ infty} ^ {2}}\ derecha) ^ {2}\ frac {1} {\ sin ^ {4}\ frac {1} {2}\ chi}
\ end {ecuación}

\ (\ begin {ecuación}
\ text {(Recordemos} k=\ frac {1} {4\ pi\ varepsilon_ {0}} Z_ {1} Z_ {2} e^ {2}\ text {en unidades MKS.})
\ end {ecuación}\)