18.2: Oscilador Accionado Amortiguado
- Page ID
- 130427
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
El oscilador accionado amortiguado lineal:
\ begin {ecuación}
\ ddot {x} +2\ lambda\ punto {x} +\ omega_ {0} ^ {2} x =( f/m) e^ {i\ Omega t}
\ end {ecuación}
(Siguiendo la notación de Landau aquí, tenga en cuenta que significa que la fuerza de arrastre de fricción real es\(2 \lambda m \dot{x}\))
Buscando cerca de la resonancia para soluciones de estado estacionario a la frecuencia de conducción, con amplitud\(b\), retraso de fase\(\delta\), es decir,
\(x(t)=b e^{i(\Omega t+\delta)}\), encontramos
\ begin {ecuación}
b e^ {i\ delta}\ izquierda (-\ Omega^ {2} +2 i\ lambda\ Omega+\ omega_ {0} ^ {2}\ derecha) =( f/m)
\ end {ecuación}
Para una frecuencia de conducción casi resonante\(\Omega=\omega_{0}+\varepsilon\), y suponiendo que la amortiguación sea lo suficientemente pequeña como para que podamos dejar caer el\(\varepsilon \lambda\) término junto con\(\varepsilon^{2}\), los términos de orden principal dan
\ begin {ecuación}
b e^ {i\ delta} =-f/2 m (\ varepsilon-i\ lambda)\ omega_ {0}
\ end {ecuación}
así que la respuesta, la dependencia de la amplitud de oscilación en la frecuencia, es a esta precisión
\ begin {ecuación}
b=\ frac {f} {2 m\ omega_ {0}\ sqrt {\ left (\ Omega-\ omega_ {0}\ derecha) ^ {2} +\ lambda^ {2}}} =\ frac {f} {2 m\ omega_ {0}\ sqrt {\ varepsilon^ {2} +\ lambda^ {2}}}
\ final {ecuación}
(También podríamos señalar que la frecuencia resonante es en sí misma bajada por la amortiguación, pero este es otro efecto de segundo orden que ignoramos aquí).
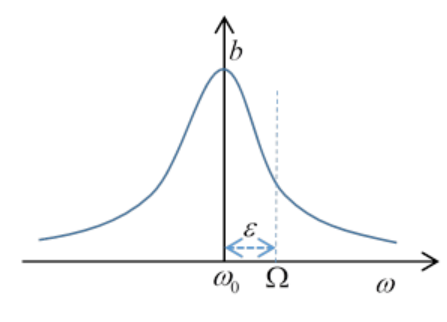
La tasa de absorción de energía es igual a la pérdida por fricción. La fuerza de fricción\(2 \lambda m \dot{x}\) sobre la masa\(\dot{x}\) que se mueve está trabajando a una velocidad:
\ begin {ecuación}
2\ lambda m\ punto {\ punto {x}} ^ {2} =\ lambda m b^ {2}\ Omega^ {2}
\ final {ecuación}
El ancho medio de la curva de resonancia en función de la frecuencia de conducción\(\Omega\) viene dado por la amortiguación. El área total bajo la curva es independiente de la amortiguación.
Para uso futuro, escribiremos la ecuación anterior para la amplitud como
\(b^{2}\left(\varepsilon^{2}+\lambda^{2}\right)=\frac{f^{2}}{4 m^{2} \omega_{0}^{2}}\)


