19.2: La Matriz Circulante- Naturaleza de sus Estados EIGENESTADOS
- Page ID
- 130867
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
La matriz que hemos construido anteriormente tiene una propiedad muy especial: cada fila es idéntica a la fila anterior con los elementos movidos sobre un lugar, es decir, tiene la forma
\ begin {ecuación}
\ left (\ begin {array} {llll}
c_ {0} & c_ {1} & c_ {2} & c_ {3}\\
c_ {3} & c_ {0} & c_ {1} & c_ {2}\
c_ {2} & c_ {3} & c_ {0} & c_ {1}\\
c_ {1} & c_ {2} & c_ {3} & c_ {0}
\ fin {array}\ derecha)
\ end {ecuación}
Tales matrices se llaman circulantes, y sus propiedades son bien conocidas. En particular, mostraremos que los vectores propios tienen la forma\(\left(1, \omega_{j}, \omega_{j}^{2}, \omega_{j}^{3}, \ldots, \omega_{j}^{N-1}\right)^{T}\) donde\(\omega_{j}^{N}=1\).
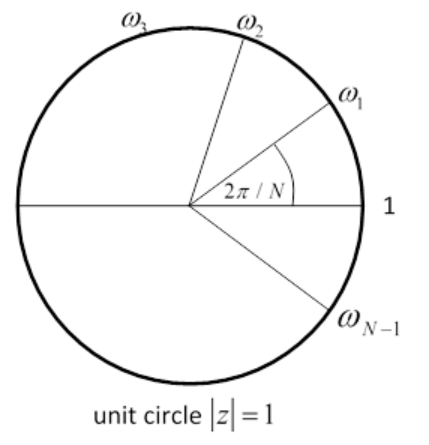
Recordemos que las raíces de la ecuación\(z^{N}=1\) son N puntos igualmente espaciados alrededor del círculo unitario,\ begin {ecuación}
e^ {2\ pi i n/N}, n=0,1,2,\ ldots N-1
\ end {ecuación}
La notación matemática estándar es etiquetar estos puntos\ (\ begin {ecuación}
1,\ omega_ {1},\ omega_ {2},\ omega_ {3},\ ldots,\ omega_ {N-1}
\ end {ecuación}\) como se muestra en la figura, pero fíjate que\(\omega_{j}=\omega_{1}^{j}\)


