22.5: Caso no lineal - Análisis de Landau

La ecuación de movimiento es:

\[\ddot{x}+2 \lambda \dot{x}+\omega_{0}^{2} x=(f / m) \cos \gamma t-\beta x^{3}\]

Establecimos anteriormente que el término cuártico no lineal trae una corrección a la frecuencia del oscilador que depende de la amplitud\(b\):

\[\omega=\omega_{0}+\frac{3 \beta b^{2}}{8 \omega_{0}}=\omega_{0}+\kappa b^{2}\]

en la notación de Landau\(\kappa=3 \beta / 8 \omega_{0}\),

La ecuación para la amplitud en el caso lineal (de la sección anterior) fue, con\(\varepsilon=\gamma-\omega_{0}\),

\[b^{2}\left(\varepsilon^{2}+\lambda^{2}\right)=\frac{f^{2}}{4 m^{2} \omega_{0}^{2}}\]

Para el caso no lineal, la amplitud máxima estará claramente en el verdadero (¡dependiente de la amplitud!) frecuencia de resonancia\(\omega(b)=\omega_{0}+\kappa b^{2} \text { so with } \varepsilon=\gamma-\omega_{0}\) antes, ahora tenemos una ecuación cúbica para\(b^{2}\):

\[b^{2}\left(\left(\varepsilon-\kappa b^{2}\right)^{2}+\lambda^{2}\right)=\frac{f^{2}}{4 m^{2} \omega_{0}^{2}}\]

Tenga en cuenta que para la fuerza motriz pequeña\(f \ll 2 m \omega_{0} \lambda, b\) es pequeña (\(b_{\max }^{2} \approx f^{2} / 4 m^{2} \omega_{0}^{2} \lambda^{2}\)) pero el centro del pico se ha desplazado ligeramente hacia arriba, a\(\varepsilon=\kappa b^{2}, \text { that is, at a driving frequency } \gamma=\omega_{0}+\kappa b^{2}\). La ecuación cúbica para solo\(b^{2}\) tiene esta solución real.

Sin embargo, a medida que aumenta la fuerza impulsora, los coeficientes de la ecuación cúbica cambian y a una fuerza crítica aparecen\(f_{k}\) dos raíces reales más.

\(\text { The } b, \varepsilon \text { curve for driving force above } f_{k} \text { looks like: }\)

Entonces, ¿qué está pasando aquí? Para un rango de frecuencias, incluyendo la línea roja discontinua vertical en la figura, parece haber tres amplitudes posibles de oscilación constante a una frecuencia. No obstante, resulta que el medio es inestable, por lo que se desviará exponencialmente, yendo a uno de los otros dos, los cuales son ambos estables.

Si el oscilador está siendo accionado a\(\omega_{0}\), y la frecuencia de conducción se incrementa gradualmente, la amplitud seguirá la curva superior hasta el punto C, luego caerá discontinuamente a la curva inferior. Un mayor aumento de frecuencia (con la misma fuerza impulsora de fuerza, por supuesto) dará una amplitud decreciente de oscilación tal como sucede para el oscilador armónico simple ordinario al alejarse de la frecuencia resonante.

Si la frecuencia ahora se baja gradualmente, la amplitud aumentará gradualmente hasta el punto D, donde saltará discontinuamente a la curva superior. La respuesta general a la frecuencia de conducción a veces se denomina histéresis, por analogía con la respuesta de un material magnético a un campo externo impuesto variable.

\(\begin{aligned}&\text { To put in some numbers, the maximum amplitude for any of these curves is when } \quad d b / d \varepsilon=0, \text { that is, }\\&\text { at } \varepsilon=\kappa b^{2}, \text { or }\end{aligned}\)

\[b_{\max }=f / 2 m \omega_{0} \lambda\]

el mismo resultado que para pequeñas oscilaciones.

Para encontrar el valor crítico de la fuerza impulsora para la que aparecen las múltiples soluciones, en la gráfica anterior es cuando C, D coinciden. Es decir,\(d b / d \varepsilon=\infty\) tiene raíces coincidentes.

Diferenciar la ecuación\(b(\varepsilon)\) para la amplitud en función de la frecuencia (y por supuesto esto es a una fuerza impulsora constante\(f\))

\[\frac{d b}{d \varepsilon}=-\frac{-\varepsilon b+\kappa b^{2}}{\varepsilon^{2}+\lambda^{2}-4 \kappa \varepsilon b^{2}+3 \kappa^{2} b^{4}}\]

C, D coinciden cuando el discriminante en el denominador cuadrático es cero, es decir, en\(\kappa^{2} b^{4}=\lambda^{2}\) donde\(\varepsilon=2 \kappa b^{2}\)

Poner estos valores en la ecuación para\(b(\varepsilon)\) como una función de la fuerza motriz f, la fuerza impulsora crítica es

\[f_{\kappa}^{2}=\frac{8 m^{2} \omega_{0}^{2} \lambda^{3}}{|\kappa|}\]

Resultados de applets numéricos

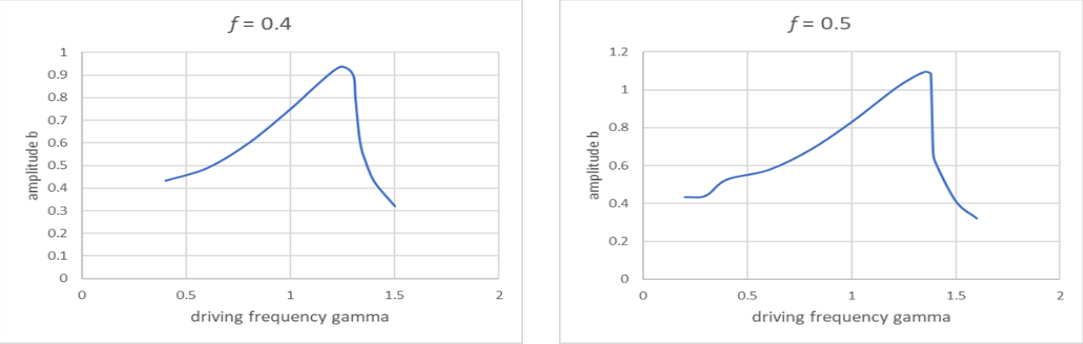
Los resultados anteriores son todos del libro de Landau, y son semicuantitativos. Se pueden verificar fácilmente usando nuestro applet en línea, que tiene una precisión del uno por ciento o mejor. Las curvas a continuación se trazan a partir de los resultados del applet, y ciertamente muestran el comportamiento predicho por Landau.

Estas parcelas son para\(\omega_{0}^{2}=m=\beta=1, \alpha=0,2 \lambda=0.34\)

\ (\ begin {aligned} &\ text {Para estos valores, Landau} f_ {k}\ text {es aproximadamente} 0.3. \ text {El nuestro se ve un poco más. Nota para} f=0.3,\ text {mostramos}\\
&\ kappa b^ {2} =0.38\ cdot (0.75) ^ {2} =0.21,\ text {cerca del pico de la gráfica.}\ end {alineado}\)