23.2: El camino hacia el caos

Ecuación de movimiento

Para el péndulo impulsado, la medida natural de la fuerza motriz es su relación con el peso\(m g\), Taylor llama a esto la fuerza motriz, por lo que para la fuerza motriz

\[F(t)=F_{0} \cos \omega t,\]

la fuerza de accionamiento\(\gamma\) se define por

\[\gamma=F_{0} / m g.\]

La ecuación de movimiento (con fuerza de amortiguación resistiva\(-b v\) y, por lo tanto, par resistivo\(-b L^{2} \dot{\phi}\)) es:

\[m L^{2} \ddot{\phi}=-b L^{2} \dot{\phi}-m g L \sin \phi+L F(t)\]

Dividiendo por\(m L^{2}\) y escribiendo el término de amortiguación\(b / m=2 \beta \) (para coincidir con la notación de Taylor, su ecuación 12.12) obtenemos (con\(\omega^2_0 = g/L\))

\[\ddot{\phi}+2 \beta \dot{\phi}+\omega_{0}^{2} \sin \phi=\gamma \omega_{0}^{2} \cos \omega t.\]

Comportamiento en el aumento gradual de la fuerza motriz: Duplicación de períodos

La fuerza motriz\(\gamma=F_{0} / m g\) es la relación adimensional entre la fuerza motriz y el peso, por lo que si éste es pequeño el péndulo no será conducido a grandes amplitudes, y de hecho encontramos que después de transitorios iniciales se asienta al movimiento a la frecuencia de conducción, cercana al caso linealizado. Esperaríamos que las cosas se complicaran más cuando las oscilaciones tienen amplitud de orden un radián, es decir, una fuerza impulsora comparable al peso. Y efectivamente lo hacen.

Aquí mostraremos que nuestro applet reproduce la secuencia encontrada por Taylor a medida que aumenta la fuerza motriz.

En la ecuación de movimiento

\[\ddot{\phi}+2 \beta \dot{\phi}+\omega_{0}^{2} \sin \phi=\gamma \omega_{0}^{2} \cos \omega t,\]

Por lo tanto, elegimos sus valores\(\omega_{0}=1.5,2 \beta =0.75, \omega=1\) y poco a poco aumentamos\(\gamma\) de\(0.9\) a\(1.0829\), donde comienza el caos.

Porque\(\gamma=0.9,\) (ver imagen) la oscilación (después de breves transitorios iniciales) se ve como una onda sinusoidal, aunque es un poco más plana, y observe que la amplitud (turquesa en caja) es mayor que\(\pi / 2\), los cambios positivos y negativos son iguales en magnitud a cinco cifras de precisión después de cinco más o menos oscilaciones.

¡Puedes verlo por ti mismo abriendo el applet! Haga clic aquí. El applet traza la gráfica, y simultáneamente muestra el péndulo oscilante (barra de clic en la parte superior derecha).

Porque\(\gamma=1.06\), hay un transitorio inicial más grande, vagamente parecido al de tres ciclos que nos reuniremos en breve. De hecho, esto se puede suprimir comenzando en\(\varphi=-\pi / 2\) (deslizador inferior a la derecha), pero todavía hay transitorios: los picos no son uniformes a una precisión de cinco cifras hasta unos cuarenta ciclos.

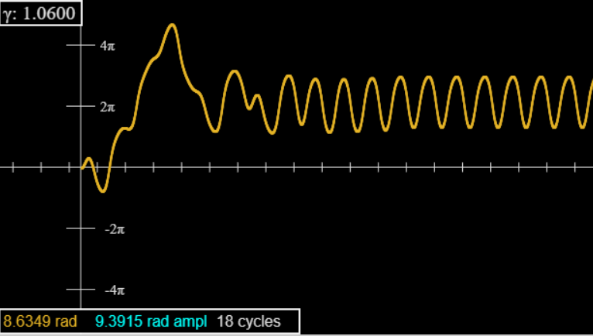
Porque\(\gamma=1.0662\), hay transitorios muy largos: no evidentes al mirar la gráfica (en el applet), sino revelados al monitorear la lectura de amplitud (figuras turquesas en el cuadro de la gráfica), el valor en el extremo más reciente.

Para superar estos transitorios, establece la velocidad del applet en 50 (esto no afecta a la precisión, solo imprime muchos menos puntos). ejecuta 350 ciclos luego pausa y ve a speed = 2. Encontrarás que los picos ahora alternan en altura a la precisión de cinco cifras que se muestra, parece que se duplica el período, pero no lo es, ejecuta algunos miles de ciclos, si tienes la paciencia, y encuentras que todos los picos tienen la misma altura. Ese fue un precursor transitorio de larga duración del período que duplicó la transición.

Al pasar a 1.0664, verás tanto picos como descensos alternando ahora en amplitud, para un periodo bien definido 2, que dura hasta 1.0792. (Mire 1.075 después de 70 ciclos más o menos y establezca el ángulo inicial en -90.)

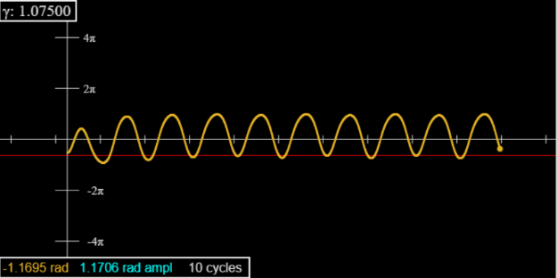
Use el control deslizante “Línea roja” justo debajo de la gráfica para verificar las alturas de picos o caídas sucesivas.

Porque\(\gamma =1.0793\), el período se duplica de nuevo: los picos sucesivos están ahora separados por el orden de 0.4 radianes, pero los picos sucesivos “altos” están repentinamente a unos 0.01 radianes de distancia. (Para verlos mejor en el applet, magnifica la escala vertical y mueva la línea roja.)

Porque\(\gamma=1.0821\) hay una duplicación adicional a un ciclo de 8, luego a 1.0827 a un ciclo de 16.

Mira la gráfica para 1.0826: en particular, la tenue línea horizontal roja cerca de la parte inferior. Cada cuarta caída va por debajo de la línea, pero las siguientes caídas más bajas se alternan entre tocar la línea y no alcanzarla del todo. Este es el ciclo 8.

Se sabe que los intervalos entre duplicaciones sucesivas disminuyen por un factor\(\delta = 4.6692\), encontrados universalmente en cascadas de duplicación de período, y llamado el número Feigenbaum, después de su descubridor. Nuestra precisión de cinco cifras es demasiado cruda para seguir esta secuencia más allá, pero podemos establecer (¡o al menos hacer muy plausible!) que más allá del límite geométrico de\(\gamma_c=1.0829\) la serie a la periodicidad desaparece (temporalmente, como veremos), el sistema es caótico. (Por supuesto, los valores de\(\gamma\) dependen del parámetro de amortiguación elegido, etc., sólo la relación de intervalos de duplicación es universal.)

De hecho, la imagen completa es compleja: hay más intervalos de periodicidad, por ejemplo un ciclo de 6 a\(\gamma=1.0845\), en la foto aquí.

Diferentes Atrayentes

Las soluciones periódicas descritas anteriormente se denominan “atractores”: configuraciones donde el sistema se asienta después de vagar inicialmente.

Claramente los atractores cambian con la fuerza motriz, lo que es menos obvio es que pueden ser diferentes para diferentes condiciones iniciales. Taylor demuestra que para\(\gamma=1.077 \) tomar\( \varphi(0)=0\) da un ciclo de 3 después de transitorios, pero\(\varphi(0)=-\pi / 2\) da un ciclo de 2. (¡Comprobado fácilmente con el applet!)

Mirando las erradas iniciales, que pueden ser bastante diferentes para cambios muy pequeños en la fuerza motriz (compare 1.0730 a 1.0729 y 1.0731, use la velocidad 5, no afecta la precisión). Pero se puede ver que estas vagabundas iniciales incluyen elementos de ambos atractores.

Ejercicio: utilizar el siguiente applet para trazar al mismo tiempo 1.0729 y 1.0730, todos los demás parámetros iguales, velocidad 5.

Ejercicio: Usa el applet para encontrar en qué ángulo se lleva a cabo la transición de un atractor a otro. Y, explore lo que sucede en una variedad de fortalezas de conducción.

Estos son los atractores más simples: hay entidades mucho más complejas, llamadas atractores extraños, discutiremos más adelante.

Ejercicios: Pruebe diferentes valores de la constante de amortiguación y vea cómo esto afecta la secuencia de bifurcación.

Sensibilidad a las Condiciones Iniciales

Recordemos que para el oscilador conducido lineal amortiguado, que puede resolverse exactamente, encontramos que cambiar las condiciones iniciales cambiaba la trayectoria, claro, pero la diferencia entre trayectorias decayó exponencialmente: las curvas convergieron.

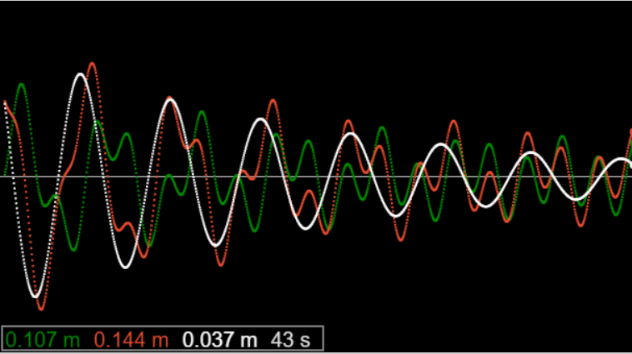
Esta ilustración es de un applet anterior: las curvas roja y verde corresponden a diferentes condiciones iniciales, la curva blanca es la diferencia entre las dos, obviamente decreciente exponencialmente, como se puede verificar analíticamente.

Para el péndulo accionado amortiguado, la imagen es más complicada. Para\(\gamma<\gamma_{c}=1.0829\) las curvas correspondientes a condiciones iniciales ligeramente diferentes convergerán (excepto, por ejemplo,\(\gamma=1.077\) donde, como se mencionó anteriormente, variando el ángulo inicial en cierto punto los interruptores forman un final de tres ciclos a uno de dos ciclos).

El exponente de Liapunov

Pues\(\gamma>\gamma_{c}\), las curvas incluso con diferencias iniciales muy pequeñas (digamos,\(10^{-4}\) radianes) se separan exponencialmente, como \(e^{\lambda t}, \lambda\)se llama el exponente Liapunov.

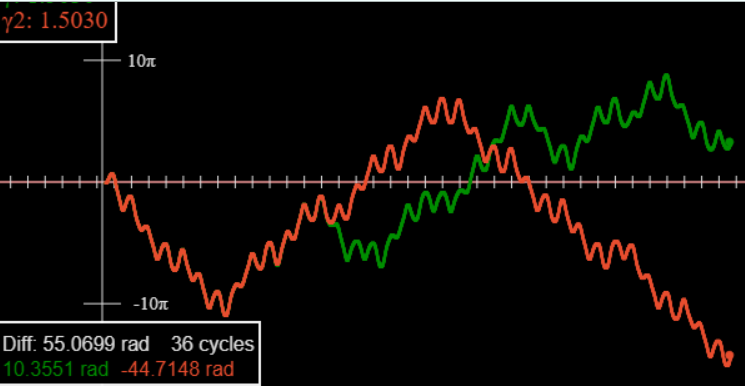
Tenga en cuenta, sin embargo, que se trata de un movimiento caótico, la divergencia no es tan suave como la convergencia que se muestra arriba para el sistema lineal. Esta gráfica es de nuestro applet de dos pistas.

Sin embargo, la naturaleza exponencial (promedio) se puede discernir trazando el logaritmo de la diferencia contra el tiempo:

Esto es de nuestro applet log difference. Está muy cerca de Taylor's fig 12.13. La pendiente de la línea roja le da al exponente Lyapunov.

(La línea roja tiene posición y pendiente ajustables).

Trazado de velocidad frente al tiempo

Como se discutió en Taylor, un mayor aumento en la fuerza impulsora más allá del umbral caótico puede conducir a breves intervalos no caóticos, como el que contiene el ciclo de seis en 1.0845 ilustrado anteriormente, pero hay dos largos tramos de comportamiento no caótico en el rango de parámetros de Taylor, de 1.1098 a 1.1482 y de 1.3 a 1.48.

En el rango de fuerza motriz más fuerte, el péndulo se mueve completamente alrededor en cada ciclo, por lo que trazar la posición contra el tiempo da una especie de gráfico de “escalera redondeada”. Comprueba esto con el applet.

La solución es trazar la velocidad contra el tiempo, y así descubrir que hay una repetición del período duplicando la ruta al caos en el extremo superior de este intervalo. Haga clic para trazar\(d\phi /dt\) en lugar de\(\phi\).

 

Trayectorias Estado-Espacio

Puede ser iluminador ver cómo el movimiento se desarrolla en el tiempo en el espacio de estado bidimensional (\(\phi, \dot{\phi}\)). (Igualmente llamado espacio de fase.) ¡Vea el applet State Space!

Ahora, para una partícula en un potencial independiente del tiempo, especificar la posición y la velocidad en un instante determinado determina el camino futuro, pero ese no es el caso aquí, la aceleración está determinada por la fase de la fuerza impulsora, que varía en el tiempo, por lo que el sistema realmente necesita tres parámetros para especificar su movimiento posterior.

Eso significa que el espacio de fase es realmente tridimensional, siendo la tercera dirección la fase de conducción, o, equivalentemente, el tiempo, pero periódica con el periodo de la fuerza motriz. En este espacio tridimensional, los caminos no pueden cruzarse, en ningún momento el camino futuro se define de manera única. Nuestras gráficas bidimensionales son proyecciones de estas trayectorias tridimensionales sobre el plano (\(\phi, \dot{\phi}\)).

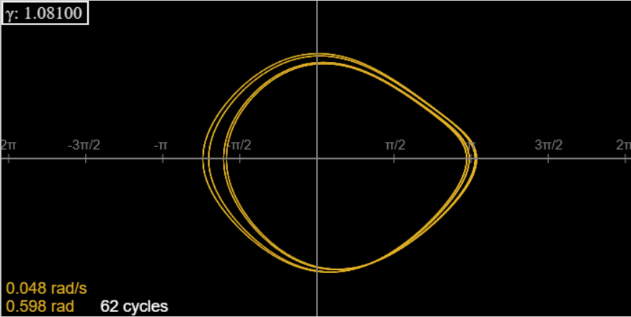
Aquí están los 4 ciclos en\(\gamma = 1.081\), menos los primeros 20 ciclos, para eliminar los transitorios.

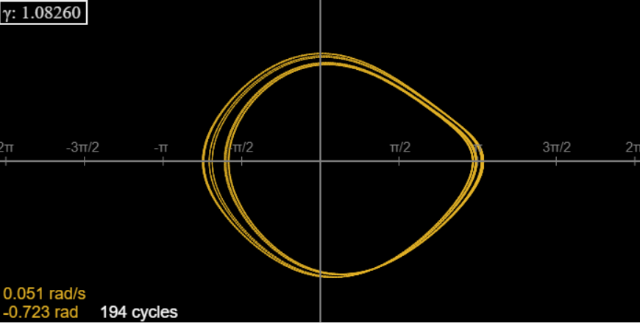
Para\(\gamma = 1.0826\), hay un ciclo de 8. Ejecute el applet durante 40 ciclos más o menos para deshacerte de los transitorios, luego mira el extremo izquierdo de la curva generada al correr, digamos, a 200 ciclos. No parece que haya 8 líneas, pero la línea más externa y las dos líneas más internas son dobles (observe el grosor). Puedes comprobarlo con el applet, haciendo una pausa en el eje y notando la lectura de posición: hay 8 valores diferentes que se repiten. (No tiene que detenerse justo en el eje, puede detenerse cerca de él y luego usar los botones de paso para llegar allí).

Porque\(\gamma = 1.0830\), el camino es caótico, ¡pero no se ve muy diferente en esta escala! Compruébalo con el applet. El caos se hace más evidente al aumentar aún más\(\gamma\). Para\(\gamma =1.087\) el patrón es “engordado” ya que los ciclos repetidos difieren ligeramente.

Para un mayor incremento en\(\gamma\), el movimiento orbital cubre más territorio: en\(\gamma = 1.1\), aquí están los primeros trescientos ciclos más o menos.

Trazando muchas órbitas a alta velocidad encontramos:

Sin embargo, aquí la historia se complica: resulta que esta serie caótica de órbitas es de hecho un transitorio, y después de unos 300 ciclos el sistema salta a un ciclo de 3, donde permanece. De hecho, hemos alcanzado un rango de\(\gamma\) (aproximadamente 1.1098 a 1.1482) donde después de transitorios iniciales (que pueden ser bastante largos) el movimiento no es caótico, sino un ciclo de 3.

Obviamente, ¡hay mucho que explorar para este sistema! Para comprender mejor estas complejidades, intentamos un enfoque diferente, desarrollado por Poincaré.

Secciones Poincaré

Al observar las imágenes anteriores, a medida que pasamos de una sola órbita a sucesivos duplicaciones de períodos y luego al caos, la forma general de la órbita no cambia drásticamente (hasta ese final de tres ciclos). Las cosas interesantes son la secuencia de duplicación, el caos y los atractores, tal vez estamos tramando demasiada información.

Para enfocarse en lo esencial, Poincaré trazó un solo punto de cada ciclo, esto ahora se llama sección de Poincaré. Para construir esto, comenzamos con la\(t = 0\) posición, etiquetarla\(P_0=(\varphi_0,\dot{\varphi}_0)\). Luego sumar el punto\(P_1=(\varphi_1,\dot{\varphi}_1)\) precisamente un ciclo después, y así sucesivamente—puntos separados un ciclo\(P_2=(\varphi_2,\dot{\varphi}_2)\), etc. Ahora bien, conocer la posición\(P=(\varphi,\dot{\varphi})\) en el espacio estatal no es suficiente información para trazar la órbita futura— también necesitamos conocer la fase de la fuerza impulsora. Pero al trazar puntos con un ciclo en el tiempo separados, todos verán la misma fuerza de inicio de fase, por lo que la transformación que nos lleva de\(P_0\) a\(P_1\) solo se repite en pasar de\(P_1\) a\(P_2\), etc.

Para ver estos puntos únicos en el applet State Space, haga clic en “Mostrar punto rojo”: al ejecutarse, el applet mostrará un punto por ciclo rojo.

Pensando momentáneamente en el espacio de fase tridimensional completo, la sección de Poincaré es una sección transversal en la fase inicial del ciclo de conducción. Hemos agregado al applet una opción de fase de punto rojo, para encontrar la sección de Poincaré en una fase diferente. Hacer esto varias veces, y mirando el movimiento de los puntos rojos, da una imagen más completa del movimiento.

Entonces la sección de Poincaré, al aumentar\(\gamma\) a través de la secuencia de duplicación (y siempre omitiendo transitorios iniciales) va de un solo punto a dos puntos, a cuatro, etc.

Para ver todo esto un poco más claramente, el siguiente applet, llamado Sección Poincaré, muestra solo un punto por ciclo, pero tiene una opción de fase para que puedas mirar cualquier etapa del ciclo.

Ejercicio: ¡mira todo esto con el applet de Poincaré! Para verlo bien, haz clic en Alternar Origen/Escala, usa los controles deslizantes para centrar el patrón, más o menos, luego escalarlo. Corre por unos cientos de ciclos, luego haz clic en Ocultar rastro seguido de Mostrar rastro para deshacerte de los transitorios.

Empezar con\(\gamma = 1.0826\). El tramo Poincaré es de ocho puntos en una curva, a 1.0827 se puede discernir 16. Para 1.0829, tenemos caos, y la sección tiene tramos finitos de la curva, no solo puntos. Se ve muy similar en 1.0831, pero—sorpresa—a 1.0830 es un conjunto de puntos (¿32?) algunos se duplicaron. Esto nos dice que estamos en un campo minado. No hay nada suave en el caos.

Aparte de las interrupciones, a medida que\(\gamma\) aumenta, la sección de Poincaré llena una curva, que luego evoluciona hacia el extraño atractor mostrado por Taylor y otros. Al pasar de 1.090 en pasos a 1.095, la curva evoluciona una segunda rama, estrechamente paralela. A 1.09650 las dos ramas son iguales en longitud, luego a 1.097 la rama inferior se extiende repentinamente una curva larga, se ve muy igual en 1.100, luego en 1.15 reconocemos la emergencia del extraño atractor.

Pero de hecho se trata de una narrativa simplificada: hay interrupciones. Por ejemplo, en\(\gamma = 1.0960\) hay un ciclo de 5, sin caos (desaparece al cambiar en 0.0001). Y a 1.12 estamos en el intervalo de 3 ciclos mencionado anteriormente.

En fin, el extraño atractor sigue reapareciendo, y en 1.5 se ve así:

Esto se ve bastante delgado en comparación con la imagen de Taylor por lo mismo\(\gamma\): la razón es que hemos mantenido la fuerte amortiguación.

Cambiando a\(2\beta =0.375\), recuperamos la imagen de Taylor. Al igual que él, mostramos aquí (desde el applet) el atractor y sucesivas ampliaciones de una parte, para dar algún indicio de la estructura fractal:

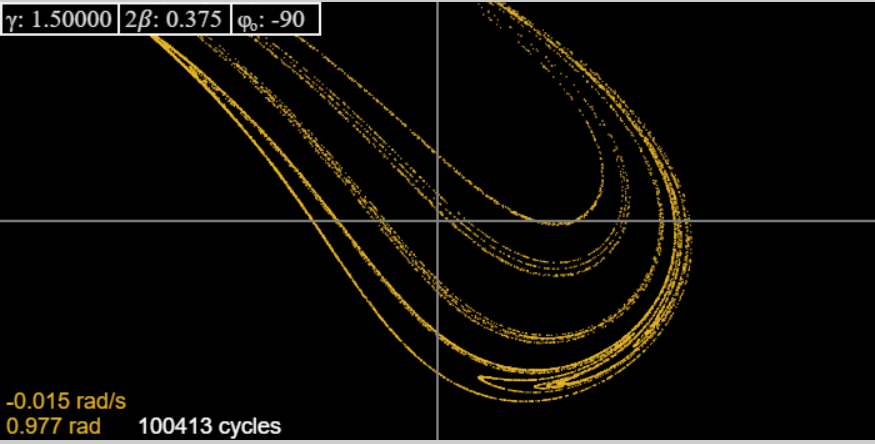
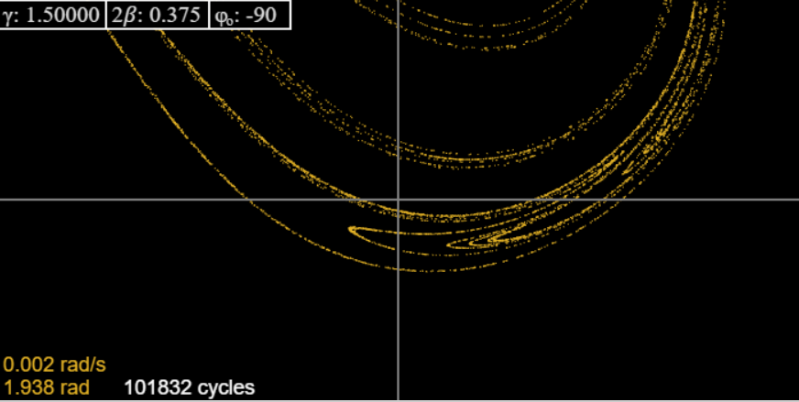
Tenemos que admitir que a la mayor ampliación la imagen de Taylor es ciertamente superior a la generada por el applet, pero no lo contradice, en realidad, nos asegura que el applet es confiable hasta el nivel de definición que es evidente al mirarlo.

Ejercicio: Utilice los dos últimos applets para explorar otras regiones del espacio de parámetros. ¿Qué sucede al variar la amortiguación? Pasar de\(2\beta =0.375\)\(2\beta =0.75\) al atractor tiene la misma forma general pero es mucho más estrecho. Después vaya en 0.001 pasos a 0.76. Para algunos valores se ve el atractor, pero para otros un ciclo, diferentes longitudes. Hay un ciclo de dos ciclos de 0.76 a 0.766, luego un ciclo de cuatro, luego a 0.78 de vuelta a un ciclo de dos, a 0.814 un ciclo. Si aumenta la fuerza motriz y la amortiguación, puede encontrar atractores extremadamente estrechos.

Ejercicio: Baker y Gollub, Dinámica caótica, página 52, dan una secuencia de secciones de Poincaré a\(0.2\pi\) intervalos para\(\gamma=1.5\) y\(2\beta =0.75\). ¡Puedes revisarlos (y los intermedios) con el applet, e intentar imaginarlos poniéndolos en una pila para visualizar el atractor tridimensional completo!