10.4: Función de disipación de Rayleigh

Como se mencionó anteriormente, los sistemas no conservadores que involucran disipación viscosa o friccional, generalmente resultan de interacciones térmicas débiles con muchos átomos cercanos, lo que hace poco práctico incluir un conjunto completo de grados de libertad activos. Además, los sistemas disipativos suelen implicar complicadas dependencias de las propiedades de velocidad y superficie que se manejan mejor al incluir la fuerza de arrastre disipativa explícitamente como una fuerza de arrastre generalizada en las ecuaciones de Euler-Lagrange. La fuerza de arrastre puede tener cualquier dependencia funcional de la velocidad, la posición o el tiempo.

\[\mathbf{F}^{drag}=-f(\mathbf{\dot{q}},\mathbf{q},t)\mathbf{\hat{v}}\]

Tenga en cuenta que dado que la fuerza de arrastre es disipativa, la componente dominante de la fuerza de arrastre debe apuntar en la dirección opuesta al vector de velocidad.

En\(1881\) Lord Rayleigh demostró que si una fuerza disipativa\(\mathbf{F}\) depende linealmente de la velocidad, se puede expresar en términos de un potencial escalar funcional de las coordenadas generalizadas llamadas función de disipación de Rayleigh\(\mathcal{R(}\mathbf{\dot{q})}\). La función de disipación Rayleigh es una forma elegante de incluir fuerzas disipativas lineales dependientes de la velocidad tanto en la mecánica lagrangiana como en la hamiltoniana, como se ilustra a continuación para la mecánica lagrangiana y hamiltoniana.

Fuerzas disipativas generalizadas para dependencia de la velocidad lineal

Considerar\(n\) ecuaciones de movimiento para los\(n\) grados de libertad, y asumir que la disipación depende linealmente de la velocidad. Entonces, permitiendo todo el acoplamiento cruzado posible de las ecuaciones de movimiento para\(q_{j},\) las ecuaciones de movimiento se puede escribir en la forma

\[\sum_{i=1}^{n}\left[ m_{ij} \ddot{q}_{j}+b_{ij}\dot{q}_{j}+c_{ij}q_{j}-Q_{i}(t)\right] =0 \label{10.5}\]

Multiplicar la ecuación\ ref {10.5} por\(\dot{q}_{i}\), tomar la integral de tiempo, y sumar\(i,j\), da la siguiente ecuación de energía\[\sum_{i=1}^{n}\sum_{j=1}^{n}\int_{0}^{t}m_{ij}\ddot{q}_{j}\dot{q} _{i}dt+\sum_{i=1}^{n}\sum_{j=1}^{n}\int_{0}^{t}b_{ij}\dot{q}_{j}\dot{q} _{i}dt+\sum_{i=1}^{n}\sum_{j=1}^{n}\int_{0}^{t}c_{ij}q_{j}\dot{q} _{i}dt=\sum_{i}^{n}\int_{0}^{t}Q_{i}(t)\dot{q}_{i}dt\]

El término de la derecha es la energía total suministrada al sistema por las fuerzas generalizadas externas\(Q_{i}(t)\) en su momento\(t\). El primer término integral de tiempo en el lado izquierdo es la energía cinética total, mientras que el tercer término integral de tiempo equivale a la energía potencial. El segundo término integral a la izquierda se define como igual\(2\mathcal{R}(\mathbf{\dot{q}} )\) donde la función de disipación de Rayeigh\(\mathcal{R}(\mathbf{\dot{q}})\) se define como

\[\mathcal{R}(\mathbf{ \dot{q}})\mathcal{\equiv }\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}b_{ij}\dot{q }_{i}\dot{q}_{j}\]

y las sumas están sobre todas\(n\) las partículas del sistema. Esta definición permite complicados efectos de acoplamiento cruzado entre las\(n\) partículas.

Los efectos de acoplamiento partícula-partícula generalmente se pueden descuidar permitiendo el uso de la definición más simple que incluye solo los términos diagonales. Entonces la forma diagonal de la función de disipación Rayleigh simplifica a

\[\mathcal{R}(\mathbf{\dot{q}})\mathcal{\equiv }\frac{1}{2}\sum_{i=1}^{n}b_{i} \dot{q}_{i}^{2}\]

Por lo tanto, la fuerza de fricción en la\(q_{i}\) dirección depende linealmente de la velocidad\(\dot{q}_{i}\), es decir

\[F_{q_{i}}^{f}=-\frac{\partial \mathcal{R}(\mathbf{\dot{q}})}{\partial \dot{q} _{i}}=-b_{i}\dot{q}_{i}\]

En general, la fuerza disipativa es el gradiente de velocidad de la función de disipación Rayleigh,\[\mathbf{F}^{f}=-\nabla _{\mathbf{\dot{q}}}\mathcal{R}(\mathbf{\dot{q}})\]

El significado físico de la función de disipación Rayleigh se ilustra calculando el trabajo realizado por una partícula\(i\) contra la fricción, que es

\[dW_{i}^{f}=-\mathbf{F}_{i}^{f}\cdot d\mathbf{r=-F}_{i}^{f}\cdot \mathbf{\dot{ q}}_{i}dt=b_{i}\dot{q}_{i}^{2}dt\]Por lo tanto

\[2\mathcal{R}(\mathbf{\dot{q}})\mathcal{=}\frac{dW^{f}}{dt}\]

que es la tasa de pérdida de energía (potencia) debida a las fuerzas disipadoras involucradas. La misma relación se obtiene después de sumar todas las partículas involucradas.

Transformar la fuerza de fricción en coordenadas generalizadas requiere ecuación\((6.3.10)\)

\[\mathbf{\dot{r}}_{i}\mathbf{=}\sum_{k}\frac{\partial \mathbf{r}_{i}}{ \partial q_{k}}\dot{q}_{k}+\frac{\partial \mathbf{r}_{i}}{\partial t}\]

Tenga en cuenta que la derivada con respecto a\(\dot{q}_{k}\) iguales

\[\frac{\partial \mathbf{\dot{r}}_{i}}{\partial \dot{q}_{j}}=\frac{\partial \mathbf{r}_{i}}{\partial q_{j}}\]

Usando ecuaciones\((6.3.11)\) y\(7.3.12\), la\(j\) componente de la fuerza de fricción generalizada\(Q_{j}^{f}\) viene dada por\[Q_{j}^{f}=\sum_{i=1}^{n}\mathbf{F}_{i}^{f}\cdot \frac{\partial \mathbf{r}_{i} }{\partial q_{j}}=\sum_{i=1}^{n}\mathbf{F}_{i}^{f}\cdot \frac{\partial \mathbf{\dot{r}}_{i}}{\partial \dot{q}_{j}}=-\sum_{i=1}^{n}\nabla _{v_{i}} \mathcal{R}(\mathbf{\dot{q}})\cdot \frac{\partial \mathbf{\dot{r}}_{i}}{ \partial \dot{q}_{j}}=-\frac{\partial \mathcal{R}(\mathbf{\dot{q}})}{ \partial \dot{q}_{j}}\label{10.15}\]

La ecuación\ ref {10.15} proporciona una expresión elegante para la fuerza disipativa generalizada\(Q_{j}^{f}\) en términos del potencial de disipación escalar de Rayleigh\(\mathcal{R}\).

Fuerzas disipativas generalizadas para dependencia de velocidad no lineal

La discusión anterior sobre la función de disipación Rayleigh se limitó al caso especial de disipación lineal dependiente de la velocidad. Virga [Vir15] propuso que el alcance del formalismo clásico de Rayleigh-Lagrange puede extenderse para incluir la disipación dependiente de la velocidad no lineal asumiendo que las fuerzas disipativas no conservadoras se definen por

\[\mathbf{F}_{i}^{f}=-\frac{\partial R(\mathbf{q},\mathbf{\dot{q}})}{\partial \mathbf{\dot{q}}}\]

donde la función de disipación Rayleigh generalizada\(\mathcal{R(}\mathbf{q}, \mathbf{\dot{q}})\) satisface la relación mecánica general de Lagrange

\[\frac{\delta L}{\delta q}-\frac{\partial R}{\partial \dot{q}}=0\]

Esta función generalizada de disipación de Rayleigh elimina la restricción previa a los procesos de disipación lineal, lo que amplía enormemente el rango de validez para usar la función de disipación de Rayleigh.

Ecuaciones de movimiento de Lagrange

Las fuerzas disipativas lineales pueden incluirse directa y elegantemente en la mecánica lagrangiana utilizando la función de disipación de Rayleigh como fuerza generalizada\(Q_{j}^{f}\). Insertar la función de disipación Rayleigh\ ref {10.15} en las ecuaciones de movimiento Lagrange generalizadas\((6.5.12)\) da

\[\left\{ \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q}_{j}}\right) - \frac{\partial L}{\partial q_{j}}\right\} =\left[ \sum_{k=1}^{m}\lambda _{k} \frac{\partial g_{k}}{\partial q_{j}}(\mathbf{q},t)+Q_{j}^{EXC}\right] - \frac{\partial \mathcal{R(}\mathbf{q},\mathbf{\dot{q}})}{\partial \dot{q}_{j} }\label{10.18}\]

donde\(Q_{j}^{EXC}\) corresponde a las fuerzas generalizadas que quedan después de la eliminación de la fuerza de fricción lineal generalizada, dependiente de la velocidad\( Q_{j}^{f}\).

Las fuerzas holonómicas de restricción son absorbidas en el término multiplicador de Lagrange.

Mecánica hamiltoniana

Si las fuerzas no conservadoras dependen linealmente de la velocidad, y son derivables de la función de disipación de Rayleigh de acuerdo con la Ecuación\ ref {10.15}, entonces el uso de la definición de impulso generalizado da

\[\begin{align} \dot{p}_{i} &=&\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{j}}=\frac{ \partial L}{\partial q_{i}}+\left[ \sum_{k=1}^{m}\lambda _{k}\frac{\partial g_{k}}{\partial q_{j}}(\mathbf{q},t)+Q_{j}^{EXC}\right] -\frac{\partial \mathcal{R(}\mathbf{q},\mathbf{\dot{q}})}{\partial \dot{q}_{j}} \\ \dot{p}_{i} &=&-\frac{\partial H(\mathbf{p,q},t\mathbf{)}}{\partial q_{i}}+ \left[ \sum_{k=1}^{m}\lambda _{k}\frac{\partial g_{k}}{\partial q_{j}}( \mathbf{q},t)+Q_{j}^{EXC}\right] -\frac{\partial \mathcal{R(}\mathbf{q}, \mathbf{\dot{q}})}{\partial \dot{q}_{j}}\end{align}\]

Así, las ecuaciones de Hamilton se convierten en

\[\begin{align} \dot{q}_{i} &=&\frac{\partial H}{\partial p_{i}} \\ \dot{p}_{i} &=&-\frac{\partial H}{\partial q_{i}}+\left[ \sum_{k=1}^{m} \lambda _{k}\frac{\partial g_{k}}{\partial q_{j}}(\mathbf{q},t)+Q_{j}^{EXC} \right] -\frac{\partial \mathcal{R(}\mathbf{q},\mathbf{\dot{q}})}{\partial \dot{q}_{j}}\end{align}\]

La función de disipación Rayleigh\(\mathcal{R(}\mathbf{q},\mathbf{\dot{q}})\) proporciona una manera elegante y conveniente de dar cuenta de las fuerzas disipativas tanto en la mecánica lagrangiana como en la hamiltoniana.

Ejemplo\(\PageIndex{1}\): Driven, Linearly-Damped, Coupled Linear Oscillators

Considere los dos osciladores acoplados idénticos, amortiguados linealmente (constante de amortiguación\(\beta\)) mostrados en la figura.

Figura\(\PageIndex{1}\): Osciladores lineales acoplados, amortiguados linealmente y accionados armónicamente.

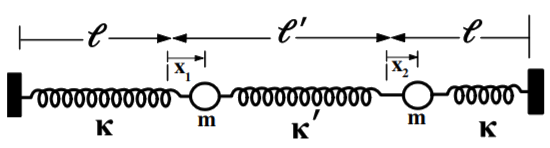
\( F=F_{0}\cos (\omega t)\)Se aplica una fuerza periódica a la masa de la izquierda\(m\). La energía cinética del sistema es

\[T=\frac{1}{2}m(\dot{x}_{1}^{2}+\dot{x}_{2}^{2})\nonumber\]La energía potencial es

\[U=\frac{1}{2}\kappa x_{1}^{2}+\frac{1}{2}\kappa x_{2}^{2}+\frac{1}{2}\kappa ^{\prime }\left( x_{2}-x_{1}\right) ^{2}=\frac{1}{2}\left( \kappa +\kappa ^{\prime }\right) x_{1}^{2}+\frac{1}{2}\left( \kappa +\kappa ^{\prime }\right) x_{2}^{2}-\kappa ^{\prime }x_{1}x_{2} \notag\]

Así el lagrangiano iguala\[L=\frac{1}{2}m(\dot{x}_{1}^{2}+\dot{x}_2^{2})-\left[ \frac{1}{2} ( \kappa +\kappa^{\prime } ) x_{1}^{2}+\frac{1}{2} ( \kappa +\kappa^{\prime } ) x_{2}^{2}-\kappa^{\prime }x_{1}x_{2}\right]\nonumber\]

Dado que la amortiguación es lineal, es posible utilizar la función de disipación Rayleigh

\[\mathcal{R=}\frac{1}{2}\beta (\dot{x}_{1}^{2}+\dot{x}_{2}^{2})\nonumber\]

Las fuerzas generalizadas aplicadas son

\[Q_{1}^{\prime }=F_{o}\cos \left( \omega t\right) \hspace{1in}Q_{2}^{\prime }=0\nonumber\]

Usa las ecuaciones de Euler-Lagrange\ ref {10.18} para derivar las ecuaciones de movimiento

\[\left\{ \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q}_{j}}\right) - \frac{\partial L}{\partial q_{j}}\right\} +\frac{\partial \mathcal{F}}{ \partial \dot{q}_{j}}=Q_{j}^{\prime }+\sum_{k=1}^{m}\lambda _{k}\frac{ \partial g_{k}}{\partial q_{j}}(\mathbf{q},t)\nonumber\]da\[\begin{aligned} m\ddot{x}_{1}+\beta \dot{x}_{1}+(\kappa +\kappa ^{\prime })x_{1}-\kappa ^{\prime }x_{2} &=&F_{0}\cos \left( \omega t\right) \\ m\ddot{x}_{2}+\beta \dot{x}_{2}+(\kappa +\kappa ^{\prime })x_{2}-\kappa ^{\prime }x_{1} &=&0\end{aligned}\]

Estas dos ecuaciones acopladas pueden desacoplarse y simplificarse haciendo una transformación a coordenadas normales,\(\eta _{1},\eta _{2}\) donde

\[\eta _{1}=x_{1}-x_{2}\hspace{1in}\eta _{2}=x_{1}+x_{2}\nonumber\]

Así\[x_{1}=\frac{1}{2}(\eta _{1}+\eta _{2})\hspace{1in}x_{2}=\frac{1}{2}(\eta _{2}-\eta _{1})\nonumber\]

Insertar estos en las ecuaciones de movimiento da

\[\begin{aligned} m(\ddot{\eta}_{1}+\ddot{\eta}_{2})+\beta (\dot{\eta}_{1}+\dot{\eta} _{2})+(\kappa +\kappa ^{\prime })(\eta _{1}+\eta _{2})-\kappa ^{\prime }(\eta _{2}-\eta _{1}) &=&2F_{0}\cos \left( \omega t\right) \\ m(\eta _{2}-\eta _{1})+\beta (\eta _{2}-\eta _{1})+(\kappa +\kappa ^{\prime })(\eta _{2}-\eta _{1})-\kappa ^{\prime }(\eta _{1}+\eta _{2}) &=&0\end{aligned}\]

Sumar y restar estas dos ecuaciones da las siguientes dos ecuaciones desacopladas

\[\begin{aligned} \ddot{\eta}_{1}+\frac{\beta }{m}\dot{\eta}_{1}+\frac{\left( \kappa +2\kappa ^{\prime }\right) }{m}\eta _{1} &=&\frac{F_{0}}{m}\cos \left( \omega t\right) \\ \ddot{\eta}_{2}+\frac{\beta }{m}\dot{\eta}_{2}+\frac{\kappa }{m}\eta _{2} &=& \frac{F_{0}}{m}\cos \left( \omega t\right)\end{aligned}\]

Definir\(\Gamma =\frac{\beta }{m},\omega _{1}=\sqrt{\frac{\left( \kappa +2\kappa ^{\prime }\right) }{m}},\omega _{2}=\sqrt{\frac{\kappa }{m}} ,A=\frac{F_{0}}{m}\). Entonces las dos ecuaciones independientes de movimiento se convierten en

\[\ddot{\eta}_{1}+\Gamma \dot{\eta}_{1}+\omega _{1}^{2}\eta _{1}=A\cos \left( \omega t\right) \hspace{1in}\ddot{\eta}_{2}+\Gamma \dot{\eta}_{2}+\omega _{2}^{2}\eta _{2}=A\cos \left( \omega t\right)\nonumber\]

Esta solución es una superposición de dos modos normales independientes, linealmente amortiguados, conducidos\(\eta _{1}\) y\(\eta _{2}\) que tienen diferentes frecuencias naturales\(\omega _{1}\) y\(\omega _{2}\). Para una amortiguación débil, estos dos modos normales impulsados experimentan cada uno un movimiento oscilatorio amortiguado con los modos\(\eta _{1}\) y\( \eta _{2}\) normales que exhiben resonancias en\(\omega _{1}^{\prime }=\sqrt{\omega _{1}^{2}-2\left( \frac{\Gamma }{2}\right) ^{2}}\) y\(\omega _{2}^{\prime }=\sqrt{\omega _{2}^{2}-2\left( \frac{ \Gamma }{2}\right) ^{2}}\)

Ejemplo\(\PageIndex{2}\): Kirchhoff’s Rules for Electrical Circuits

Las ecuaciones matemáticas que rigen el comportamiento de los sistemas mecánicos y los circuitos\(LRC\) eléctricos tienen una estrecha similitud. Así, se pueden utilizar métodos variacionales para derivar el comportamiento análogo de los circuitos eléctricos. Por ejemplo, para un sistema de circuitos\(n\) separados, el flujo magnético\(\Phi _{ik \text{ }}\) a través del circuito\(i,\) debido a la corriente eléctrica\( I_{k}=\dot{q}_{k}\) que fluye en el circuito\(k,\) viene dado por

\[\Phi _{ik}=M_{ik}\dot{q}_{k}\nonumber\]

donde\(M_{ik}\) esta la inductancia mutua. El término diagonal\(M_{ii}=L_{i}\) corresponde a la autoinductancia del circuito\(i\). El flujo magnético neto\(\Phi _{i}\) a través del circuito\(i,\) debido a todos los\(n\) circuitos, es la suma

\[\Phi _{i}=\sum_{k=1}^{n}M_{ik}\dot{q}_{k}\nonumber\]

Así, la energía magnética total\(W_{mag},\) que es análoga a la energía cinética\(T,\) se da sumando sobre todos los\(n\) circuitos para ser\[W_{mag}=T=\frac{1}{2}\sum_{i=1}^{n}\sum_{k=1}^{n}M_{ik}\dot{q}_{i}\dot{q}_{k}\nonumber\]

De igual manera, la energía eléctrica\(W_{elect}\) almacenada en la capacitancia mutua\(C_{ik}\) entre los\(n\) circuitos, que es análoga a la energía potencial,\(U,\) viene dada por

\[W_{elect}=U=\frac{1}{2}\sum_{i=1}^{n}\sum_{k=1}^{n}\frac{q_{i}q_{k}}{C_{ik}}\nonumber\]

Así, el Lagrangiano estándar para este sistema eléctrico viene dado por

\[L=T-U=\frac{1}{2}\sum_{i=1}^{n}\sum_{k=1}^{n}\left[ M_{ik}\dot{q}_{i}\dot{q} _{k}-\frac{q_{i}q_{k}}{C_{ik}}\right] \tag{$\alpha $} \label{alpha}\]

Suponiendo que se obedece la Ley de Ohm, es decir, la fuerza de disipación depende linealmente de la velocidad, entonces la función de disipación Rayleigh se puede escribir en la forma

\[\mathcal{R\equiv }\frac{1}{2}\sum_{i=1}^{n}\sum_{k=1}^{n}R_{ik}\dot{q}_{i} \dot{q}_{k} \tag{$\beta $} \label{beta}\]

donde\(R_{ik}\) está la matriz de resistencia. Así, la fuerza de disipación, expresada en voltios, viene dada por

\[F_{i}=-\frac{\partial \mathcal{R}}{\partial \dot{q}_{j}}=\frac{1}{2} \sum_{k=1}^{n}R_{ik}\dot{q}_{k} \label{gamma} \tag{$\gamma $}\]

Insertando ecuaciones\ ref {alpha},\ ref {beta}, y\ ref {gamma} en la Ecuación\ ref {10.18}, además de hacer la suposición de que una fuerza eléctrica generalizada adicional\(Q_{i}=\xi _{i}(t)\) voltios está actuando sobre el circuito\(i,\) entonces las ecuaciones de Euler-Lagrange dan las siguientes ecuaciones de movimiento.

\[\sum_{k=1}^{n}\left[ M_{ik}\ddot{q}_{k}+R_{ik}\dot{q}_{k}+\frac{q_{k}}{C_{ik} }\right] =\xi _{i}(t)\nonumber\]

Esta es una versión generalizada de la regla de bucle de Kirchhoff que se puede ver considerando el caso donde el término diagonal\(i=k\) es el único término distinto de cero. Entonces

\[\left[ M_{ii}\ddot{q}_{i}+R_{ii}\dot{q}_{i}+\frac{q_{i}}{C_{ii}}\right] =\xi _{i}(t)\nonumber\]

Esta suma de los voltajes es idéntica a la expresión habitual de la regla de bucle de Kirchhoff. Este ejemplo ilustra el poder de los métodos variacionales cuando se aplican a campos más allá de la mecánica clásica.