2.4: Integrales de trayectoria estacionaria y variables complejas

Funciones analíticas

Supongamos que tenemos una función compleja\(f = u + iv\) de una variable compleja\(z = x + iy\), definida en alguna región del plano complejo, donde\(u\),\(v\),\(x\),\(y\) son reales. Es decir,\[ f(z) = u(x,y) + i v(x,y), \label{2.4.1}\]

con\(u(x,y)\) y funciones\(v(x,y)\) reales en el plano.

Ahora asumimos que en esta región\(f(z)\) es diferenciable, es decir,\[ \dfrac{df(z)}{dz} = \lim _{\Delta z \rightarrow 0} \dfrac{f(z + \Delta z)-f(z)}{\Delta z} \label{2.4.2}\]

está bien definido. ¿Qué nos dice esto sobre las funciones\(u(x,y)\) y\(v(x,y)\), las partes reales e imaginarias de\(f(z)\)?

De hecho, ¡la propiedad de diferenciabilidad para una función de una variable compleja nos dice mucho! No sólo significa que la función es razonablemente suave. La diferencia crucial con respecto a una función de una variable real es que\(\Delta z\) puede acercarse a cero desde cualquier dirección en el plano complejo, y el límite en estas diferentes direcciones debe ser el mismo. Por supuesto, sólo hay dos direcciones independientes, así que lo que realmente estamos diciendo es\[ \frac{\partial f(x+iy)}{\partial x}=\frac{\partial f(x+iy)}{\partial (iy)}, \label{2.4.3}\]

que podemos escribir en términos de\(u,\; v\):\[ \frac{\partial u(x,y)}{\partial x}+i\frac{\partial v(x,y)}{\partial x}=\frac{\partial u(x,y)}{\partial (iy)}+i\frac{\partial v(x,y)}{\partial (iy)}. \label{2.4.4}\]

Equiparando partes reales e imaginarias de esta ecuación encontramos:\[ \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}, \;\; \frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y}. \label{2.4.5}\]

Estas se llaman las ecuaciones de Cauchy-Riemann.

De ello se deduce inmediatamente que ambos\(u(x,y)\) y\(v(x,y)\) deben satisfacer la ecuación bidimensional laplaciana,\[ \frac{\partial^2 u(x,y)}{\partial x^2}+\frac{\partial^2 u(x,y)}{\partial y^2}=0, \label{2.4.6}\]

es decir,\[ \nabla^2u=0\;\; and\;\; \nabla^2v=0. \label{2.4.7}\]

Observe que esto implica (al igual que para un potencial electrostático) que\(u(x,y)\) no puede tener un mínimo absoluto o máximo dentro de la región de analitticidad. Si\(df(z)/dz = 0\), pero las derivadas parciales de segundo orden son distintas de cero, entonces deben tener signo opuesto, señalando una silla de montar. En el caso general, se puede utilizar una versión bidimensional del teorema de Gauss para mostrar que no hay extremo local.

Además,\[ \nabla u\cdot\nabla v=\left( \frac{\partial u}{\partial x},\frac{\partial u}{\partial y}\right) \cdot\left( \frac{\partial v}{\partial x},\frac{\partial v}{\partial y} \right) =0. \label{2.4.8}\]

Es decir, las curvas de nivel de constante\(u(x,y)\) están en todas partes ortogonales a las curvas de nivel de constante\(v(x,y)\). (El gradiente es ortogonal a las curvas de nivel en todas partes.) El punto importante es que solo exigir la diferenciabilidad de una función de una variable compleja impone una fuerte restricción a sus partes reales e imaginarias, las funciones\(u(x,y)\) y\(v(x,y)\).

Ejemplo\(\PageIndex{1}\)

Un Ejemplo Sencillo:\(f (z) = z^2\).

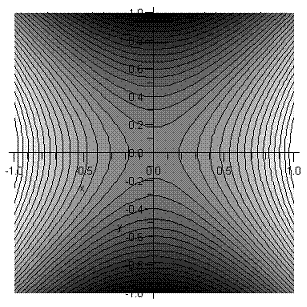
Vale la pena construir una imagen clara de las partes reales e imaginarias de la función\(z^2\). La parte real es\(x^2-y^2\), y sus curvas de nivel en el cuadrado - 1 a 1 se muestran a continuación. Los tonos más oscuros son el suelo inferior. En el origen, hay una punta de silla con terreno más alto en ambas direcciones del eje real, terreno inferior en las direcciones imaginarias puras. Las líneas\(x = y\),\(x=-y\) (no mostradas) son contornos al mismo nivel (cero) que el origen.

¿Y la parte imaginaria? \(Im\, z^2=2xy\)tiene contornos:

Poniendo los dos conjuntos de curvas de nivel en un mismo diagrama es claro que siempre se cortan ortogonalmente:

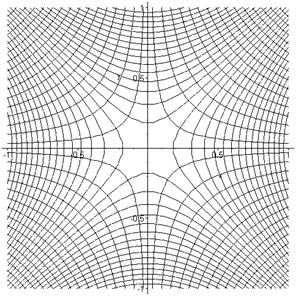
(Por cierto, esta imagen tiene una realización física. Representa las líneas de campo y equipotenciales de un imán cuadrupolar, utilizado para enfocar haces de partículas cargadas).

Ejemplo\(\PageIndex{2}\)

\(f(z) = 1/z\)

La definición de diferenciación anterior se puede utilizar para demostrar que\[ \frac{d}{dz}\frac{1}{z}=-\frac{1}{z^2} \label{2.4.9}\]

al igual que para una variable real, por lo que la función se puede diferenciar en todas partes en el plano complejo excepto en el origen. La singularidad en el origen se denomina “polo”, por razones obvias.

Integración de Contorno: Teorema de Cauchy

El teorema de Cauchy establece que la integral de una función de una variable compleja alrededor de un contorno cerrado en el plano complejo es cero si la función es analítica en la región encerrada por el contorno.

Este teorema se puede probar en varios niveles de rigor, daremos una prueba de físico básico usando el teorema de Stokes, que la integral de una función vectorial alrededor de un contorno (ahora en ordinario, no complejo, espacio) es igual a la integral del rizo de esa función sobre un área que abarca el contorno, siempre que, por supuesto, el rizo esté bien definido en todas partes de la zona,

\[ \oint \vec P\cdot\vec {ds}=\int curl\,\vec P\cdot d\vec A. \label{2.4.10}\]

Tomando el caso especial donde el contorno y el área están confinados al plano x, y y la escritura\(\vec P=(P,Q)\)\(curl\,\vec P=(\partial Q/\partial x-\partial P/\partial y)\), y el teorema de Stokes se convierte en:

\[ \oint(Pdx+Qdy)=\iint \left( \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) dxdy, \label{2.4.11}\]

conocido en esta forma como teorema de Green (y fácil de probar: los dos términos son por separado iguales,

\[\oint Qdy=\iint(\partial Q/\partial x)dxdy.\]

Esto se puede establecer dividiendo el área en franjas de ancho infinitesimal\(dy\) paralelas al eje x, integrándose con respecto a\(x\) dentro de una tira, para dar\(\int_{strip}(\partial Q/\partial x)dx=Q(x_2,y_1)-Q(x_1,y_1)\), las coordenadas de los puntos en el contorno en los extremos de la tira, luego sumando las contribuciones de todas las tiras paralelas solo da la integral alrededor del contorno.)

Ahora de vuelta al plano complejo: escribir como antes\[ z=x+iy, \;\; f(z)=u(x,y)+iv(x,y) \label{2.4.12}\]

de la cual

\[ \oint f(z)dz=\oint(u+iv)(dx+idy)=\oint(udx-vdy)+i\oint(vdx+udy). \label{2.4.13}\]

Ahora aplica el teorema de Green a las dos integrales de la derecha, reemplazando\(P,\; Q\) con primero\(u,\; -v\) luego con\(v,\; u\). Esto da:

\[ \iint \left( -\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right) dxdy+i\int \int \left( \frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}\right) dxdy \label{2.4.14}\]

y ambas integrales son idénticas a cero de las ecuaciones de Cauchy-Riemann.

Entonces, la integral de una función de una variable compleja alrededor de un contorno cerrado en el plano complejo solo puede depender del comportamiento no analítico dentro del contorno. Considera por ejemplo un polo, tomemos el caso más sencillo de integrar\(1/z\) alrededor del círculo unitario, la dirección convencional es en sentido antihorario. Entonces\(1/z=e^{-i\theta}\),\(dz=ie^{i\theta}d\theta\),\[ \oint \frac{dz}{z}=\oint id\theta=2\pi i. \label{2.4.15}\]

A esto se le llama el residuo en el polo.

Moviendo el Contorno de Integración

El teorema de Cauchy tiene una consecuencia muy importante: para una integral desde, digamos,\(z_a\) hasta\(z_b\) en el plano complejo, mover el contorno en una región donde la función es analítica no afectará el resultado, porque la diferencia entre la integral sobre el contorno original y aquella sobre la desplazada contorno es una integral alrededor de un circuito cerrado, y por lo tanto cero, siempre que la función sea analítica en la región encerrada.

Para una integral alrededor de un contorno cerrado, si las únicas singularidades encerradas por el contorno son polos, el contorno puede encogerse y romperse para convertirse en una suma de pequeños contornos separados, uno alrededor de cada polo, entonces la integral alrededor del contorno original es la suma de los residuos en los polos.

Otras Singularidades: Cortes, Hojas, etc.

Por supuesto, los polacos no son las únicas singularidades posibles. Por ejemplo,\(\log z\) tiene una singularidad en el origen. Ahora,\(\log z=\log re^{i\theta}=\log r+i\theta\). La singularidad en el origen es del\(\log r\) término, pero fíjense que si damos la vuelta al círculo unitario,\(\theta\) aumenta en\(2\pi\), y si volvemos a dar la vuelta aumenta un más\(2\pi\). Esto significa que el valor de no\(\log z\) está definido de manera única: cualquier punto dado en el plano complejo tiene valores que difieren en\(2n\pi i\),\(n\) cualquier entero. Esto se maneja reemplazando el plano complejo único por un montón de hojas, y un corte que sale del origen. Para encontrar\(\log z\), necesitas saber no solo\(z\), sino también en qué hoja estás: subir una hoja significa que\(\log z\) ha aumentado en\(2\pi i\). Cuando cruzas el corte, vas a la siguiente hoja, como una cochera de estacionamiento multinivel. El corte puede salir del origen en cualquier dirección, la disposición estándar es a lo largo del eje real, ya sea positivo o negativo.

La función de raíz cuadrada de manera similar tiene un corte, pero sólo dos hojas.

Evaluación de Integrales Rápidamente Oscilantes por Descenso Más Empinado

Cómo evaluar\(\int_{-\infty}^{\infty} e^{iax^2}dx\) de manera inequívoca: una introducción a mover el contorno de la integración y el Método de Descenso Más Inclinado.

La familiar integral gaussiana\(\int_{-\infty}^{\infty} e^{-ax^2}dx=\sqrt{\frac{\pi}{a}}\) es fácil de entender. Trazando el integrando, (aquí para\(a=1\)) hay un pico de altura 1 y ancho de orden\(1/\sqrt{a}\).

Pero, ¿qué pasa con el resultado\(\int_{-\infty}^{\infty} e^{-iax^2}dx=\sqrt{\frac{\pi}{ia}}\)? ¡Este resultado (correcto) es mucho menos obvio! Aquí el integrando siempre\(e^{-iax^2}\) está en el círculo unitario en el plano complejo, e igual a 1 at\(x=0\). Es instructivo trazar la fase del\(\varphi(x)=-ax^2\) integrando en función de\(x\) (tomando\(a = 1\) en la gráfica a continuación).

La fase es estacionaria en el origen, por lo que las contribuciones de esa región se suman coherentemente. Para ayudar a visualizar mejor el integrand, aquí hay una trama de la parte real:

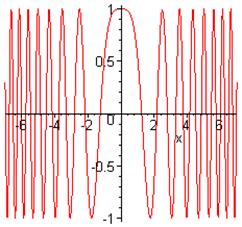
Es evidente que casi toda la contribución a la integral proviene de la región central donde la fase es estacionaria, las oscilaciones cada vez más rápidas alejándose del origen asegurando que muy poco viene de otra parte.

Entonces, ¿cómo evaluamos realmente la integral? En el plano complejo\(z=x+iy\), podemos escribir

\[ I=\int_{-\infty}^{\infty} e^{-iaz^2}dz\;\; (along\: real\: axis)\; =\int_{-\infty}^{\infty} e^{-ia(x^2-y^2+2ixy)}dz. \label{2.4.16}\]

Observe que la amplitud (o módulo) del integrando\(e^{2axy}=1\) sobre el eje real, por lo que no va a cero en el infinito, aunque esencialmente no hay contribuciones de grandes\(x\) debido a las rápidas oscilaciones.

Una forma más limpia de ver lo que está pasando es rotar el contorno de integración alrededor del origen a la línea de 45 grados\(x=-y\). Es seguro hacerlo porque la amplitud del integrando disminuye al pasar del eje real a la región\(xy < 0\), y de hecho tiende a cero al ir al infinito en esa región.

(Para dar un argumento más preciso, supongamos que sustituimos la integral infinita por una de\(-L\) a \(L\), así estaremos tomando el límite de\(L\) ir al infinito al final. Entonces el contorno distorsionado tiene primero una parte vertical, de\((-L,0)\) a\((-L,L)\) continuación el contorno diagonal de\((-L, L)\) a\((L, ­-L)\), finalmente otra pata vertical de\((L,-L)\) a\((L, 0)\). Ahora bien, en la primera parte vertical, la integral es claramente menor que la integral del módulo, es decir,

\[ \int_{(-L,0)}^{(-L,L)} e^{-ia(x^2-y^2+2ixy)}dz<\int_{0}^{L} e^{-2aLy}dy<\int_{0}^{\infty} e^{-2aLy}dy=1/2aL \label{2.4.17}\]

por lo que en el límite del ser integral original sobre todo el eje real, las contribuciones de las partes verticales del contorno desaparecen.

La integral se convierte\(\int_{-\infty}^{\infty} e^{-2ax^2}dz\) with \(dz=\sqrt{2}e^{-i\pi/4}dx\), so \[ I=\sqrt{2}e^{-i\pi/4}\int_{-\infty}^{\infty} e^{-2ax^2}dx=\sqrt{2}e^{-i\pi/4}\sqrt{\frac{\pi}{2a}}=\sqrt{\frac{\pi}{ia}}, \label{2.4.18}\]

el resultado requerido.

Método general de descenso más empinado

De hecho, el truco de rotación de contorno utilizado anteriormente para facilitar la evaluación de la integral es un caso particular de un método que tiene amplia aplicabilidad en la evaluación de integrales de contorno de la forma\(\int e^{iaf(z)}dz\). La estrategia básica es distorsionar el contorno de integración en el plano z complejo para que la amplitud del integrando sea lo más pequeña posible sobre la mayor cantidad posible del contorno de integración. En realidad, eso es exactamente lo que hicimos en el ejemplo anterior. Para ver esto, es útil trazar las curvas de nivel (líneas de valor constante) del módulo del integrando,\(|e^{-iax^2}|=e^{2axy}\).

La convención aquí es blanca para la tierra alta, negra para los valles.

Queremos mantener el contorno de integración lo más bajo posible durante el mayor tiempo posible. El mapa de arriba es de una “silla de montar”: cerros se elevan al noreste y al suroeste del origen, los valles caen hacia el noroeste y sureste. La estrategia es permanecer en los valles (pequeño integrando) tanto como sea posible, sin embargo, para llegar de\(-\infty\) a\(+\infty\) tenemos que ir de un valle a otro, y eso significa pasar por encima de la silla de montar en el origen. Obviamente, para obtener el integrando lo más pequeño posible en todas las etapas de la integración debemos bajar desde la alforja en ambas direcciones por la ruta más empinada posible, y es evidente que esto es justo abajo del centro del valle, justo el contorno que elegimos arriba. Tenga en cuenta que este camino de descenso más empinado también es uno de fase estacionaria. Esto se debe a que para cualquier función analítica de una variable compleja\(f(z)\), las líneas de constante\(Re\, f(z)\) son perpendiculares a las de constante\(Im\, f(z)\). Para una función\(e^{f(z)}\), la línea de descenso más empinada es perpendicular a las líneas de constante\(Re\, f(z)\), y por lo tanto es una línea de constante\(Im\, f(z)\), es decir, fase constante de\(e^{f(z)}\).

Puntos de sillín de funciones analíticas

Supongamos que tenemos una función\(f(z)\) analítica en alguna región\(R\) del plano complejo, y en algún momento\(z_0\) dentro de\(R\) la derivada\(\frac{df(z)}{dz} = 0\). Luego en el barrio de\(z_0\),\[ f(z) = f(z_o) + \dfrac{1}{2} f''(z_o)(z-z_o)^2 + ... \label{2.4.19}\]

Lo suficientemente cerca como para\(z_0\) que podamos descuidar los términos de orden superior, y para el caso de lo\(f''(z_o)\) real, las curvas de nivel de las partes real e imaginaria de\(f(z)\) serán entonces exactamente las que hemos trazado para\(z^2\) arriba. Para\(f''(z_o)\) complejo, las parcelas se rotarán un ángulo igual a la fase de\(f''(z_o)\). Es decir, para cualquier función analítica, cerca de cualquier punto donde\(df(z)/dz = 0\), las partes real e imaginaria de la función tengan puntos de sillín con mapas de contorno girados versiones de las anteriores.

Integración a través de una Saddlepoint

Consideramos ahora integrales de la forma\[\int_C e^{f(z)}dz \label{2.4.20}\]

donde\(C\) hay algún camino en una región donde\(f(z)\) es analítico. Esto significa que el valor de la integral no se verá afectado por distorsionar el camino, siempre que se mantenga en la región de la analíticidad. (El camino de integración suele llamarse el contorno de integración, lo llamaremos ruta aquí, para evitar confusiones con nuestros contornos, que tienen el significado geográfico estándar, uniendo puntos que tienen el mismo valor de algún parámetro).

Nótese que con la forma exponencial del integrando, la parte real de\(f(z)\) determina la magnitud del integrando, la parte imaginaria de\(f(z)\) determina su fase.

La estrategia es disponer el camino de integración para que tanto como sea posible de él esté en los valles, donde el integrando es pequeño, para luego repasar la punta de silla por la ruta más empinada posible, que estaría permaneciendo en el eje imaginario en el caso de\(z^2\) trazada arriba. Es importante señalar que esta ruta de “descenso más empinado” es también un camino por el que la parte imaginaria de\(f(z)\) permanece constante, por lo que las aportaciones a lo largo de este camino están todas en fase, es decir, se suman coherentemente.

La conclusión es que al dirigir el camino de integración a través del sillín a lo largo de la ruta más empinada para la magnitud del integrando, las mayores contribuciones a la integral están todas en fase. A lo largo de este camino, la integral tiene forma gaussiana estándar. Si la función f (z) es suficientemente grande, puede ser que se pueda descuidar la contribución de la integral alejada de la alforja. Por lo tanto, este método suele ser valioso en los casos en que algún parámetro se vuelve grande: damos una serie de ejemplos para aclarar este punto.

Estimación de Saddlepoint de\(n!\)

Utilizamos la identidad

\[ n!=\int_0^{\infty} t^ne^{-t}dt=\int_0^{\infty} e^{f(t)}dt \;\; with \;\; f(t)=n\ln t-t. \label{2.4.21}\]

A la imagen\(t^ne^{-t}\), aquí está para\(n=10\):

Tenga en cuenta que

\[ f'(t)=\frac{n}{t}-1,\;\; f'=0\: for\: t=n, \;\; f''(t)=-\frac{n}{t^2}. \label{2.4.22}\]

Por lo tanto, en la vecindad del valor máximo de\(f(t)\) at\(t=n\),\[ f(t)=n\ln n-n-\frac{1}{2n}(t-n)^2+higher\, order\, terms. \label{2.4.23}\]

Para integer\(n\), la función es analítica en cualquier región finita del plano complejo. Tomando\(n=10\), como en el gráfico de eje real anterior, y trazando los contornos de\(Re\, t^ne^{-t}\) en la vecindad de\(t=10\), encontramos:

Es evidente que la integral a lo largo del eje real es de hecho un camino de descenso más empinado. La razón por la que miramos este caso sencillo es para ganar algo de experiencia sobre cuándo es razonable desechar toda la contribución a la integral excepto la cercana a la silla de montar. Si simplemente tomamos\[ f(t)=f(n)-\frac{1}{2n}(t-n)^2=n\ln n-n-\frac{1}{2n}(t-n)^2 \label{2.4.24}\]

y tomar la\(t\) integración para estar sobre todo el eje real, no solo positivo\(t\), es una integral gaussiana y\[ n!=\int_0^{\infty} e^{f(t)}dt \cong e^{f(n)}\int_0^{\infty} e^{-(1/2n)(t-n)^2}dt=\sqrt{2\pi n}n^n e^{-n}. \label{2.4.25}\]

Los métodos más precisos, y considerablemente más complicados, dan la corrección principal a esta expresión. Está abajo por un factor de\(1/12n\), por lo que el resultado ingenuo gaussiano de la punta de silla de montar es preciso dentro de 1% para\(n = 10\), y mejora a medida que\(n\) aumenta.

La función Delta

Recordemos que la función delta puede definirse por el límite de una integral gaussiana

\[ \delta(x)=\lim_{\Delta\to0}\frac{1}{(4\pi \Delta^2)^{1/2}}e^{-x^2/4\Delta^2}. \label{2.4.26}\]

Es fácil ver cómo esto lleva a\[ \int f(x)\delta(x)dx=f(0) \label{2.4.27}\]

para una integral a lo largo del eje real con una función\(f(x)\) razonablemente bien comportada cerca del origen. Shankar menciona que la definición también funciona aunque\(\Delta^2\) sea reemplazada por\(i\Delta^2\). En ese caso, el valor absoluto de la función es el mismo en todas partes en el eje real, y aumenta a medida que\(\Delta^{-1}\) al tomar\(\Delta\) pequeñas. La razón por la que aún funciona es que las oscilaciones de fase son tan rápidas en todas partes excepto en el origen, donde la fase es momentáneamente estacionaria, por lo que toda la contribución viene de ahí.

Sin embargo, es más fácil creer\[ \delta(x)=\lim_{\Delta\to0}\frac{1}{(4\pi i\Delta^2)^{1/2}}e^{-x^2/4i\Delta^2} \label{2.4.28}\]

al entrar en el plano complejo. Si cambiamos variables de\(x\) a\(x\), donde\(x^2=ix^2\), la integral vuelve a convertirse en un simple gaussiano real. Pero, considerando\(x\) como una variable compleja, transformar a\(x\) es apenas equivalente a rotar los ejes por\(\pi/4\), o multiplicar por la raíz cuadrada de\(i\). La ruta de descenso más empinada a través del origen es ahora a lo largo de la línea\(\pi/4\) al eje real. Entonces esta es una definición perfectamente buena de la\(\delta\) función -siempre que podamos distorsionar el camino de integración desde el eje real hasta la línea\(x = y\). (Estrictamente hablando, el camino incluiría ahora dos octantes de un círculo muy grande\(R\) —su contribución se desvanece en el límite de\(R\) ir al infinito).