9.2: La transición de los peierls - un aislante inesperado

Introducción: Buscar superconductores y encontrar aisladores

En 1964, Little sugirió (Phys. Rev 134, A1416) que podría ser posible sintetizar un superconductor a temperatura ambiente utilizando materiales orgánicos en los que los electrones viajaban a lo largo de ciertos tipos de cadenas, efectivamente confinadas a una dimensión. La primera teoría satisfactoria de la superconductividad “ordinaria”, la de Bardeen, Cooper y Schrieffer (BCS) había aparecido unos años antes, en 1957. El punto clave fue que los electrones se unieron en pares de espín opuestos, y a temperaturas suficientemente bajas estos pares unidos, al ser como bosones, formaron un condensado coherente —todos los pares tenían el mismo impulso total, por lo que todos viajaron juntos, una supercorriente. El bloqueo de los electrones en este condensado eliminó efectivamente la dispersión habitual de un solo electrón por impurezas que degrada las corrientes ordinarias en los conductores.

Pero, ¿qué podría unir a los electrones que repelen electrostáticamente? La respuesta resultó ser distorsiones de celosía, como sugirió por primera vez Fröhlich en 1950. Un electrón que viaja a través del cristal atrae a los iones positivos, el consiguiente exceso de carga positiva local atrae a otro electrón. La fuerza de esta unión, y por lo tanto la temperatura a la que tiene lugar la transición superconductora, depende de la rapidez de la respuesta de la red. Esto fue confirmado por el efecto isótopo: el tiempo de respuesta de la red obviamente depende de la inercia de la red, la teoría de BCS predijo que para un elemento superconductor con diferentes variedades isotópicas, la relación de las temperaturas de transición superconductoras para isótopos puros\(T_2/T_1\) fue igual a \(\sqrt{M_1/M_2}, M_1,M_2\)siendo las masas de iones, teniendo el isótopo más ligero la temperatura de transición más alta. Este fue efectivamente el caso.

La idea de poco era que la acumulación de carga positiva por un electrón que pasaba podría acelerarse drásticamente si en lugar de tener que mover iones, solo necesita reorganizar otros electrones. Desafortunadamente, no había materiales candidatos tridimensionales obvios. Sin embargo, si los electrones de conducción se movían a lo largo de una cadena unidimensional, se podrían unir cadenas laterales polarizables, y el reordenamiento de la distribución de carga electrónica en estas cadenas laterales respondería muy rápidamente a un electrón de conducción que pasaba, acumulando una carga positiva local. Si esto funcionaba, los argumentos de orden de magnitud sugirieron una posible mejora de la temperatura de transición por un factor\(\sqrt{M/m}\) sobre los superconductores ordinarios,\(m\) siendo la masa electrónica.

En la década de 1970, se sintetizaron y probaron diversos materiales orgánicos, comenzando por uno llamado TTF-TCNQ, en el que un conjunto de moléculas largas similares a polímeros donaron electrones a otro conjunto, dejando conductores unidimensionales con bandas parcialmente rellenas (ver más adelante), aparentemente buenos candidatos para la superconductividad. Desafortunadamente, al enfriarse, ¡estos materiales sorprendentemente se convirtieron en aislantes en lugar de superconductores! Este fue el primer ejemplo de una transición de Peierls, un fenómeno generalizado en sistemas cuasi unidimensionales.

El mecanismo básico de la transición de Peierls se puede entender con un modelo simple. Es un buen ejemplo de teoría aplicada de perturbación de segundo orden, incluyendo el caso degenerado. Examinamos el modelo y el resultado a continuación. Cabe agregar que en algunos materiales más nuevos la transición de Peierls se suprime (inesperadamente) bajo alta presión, y de hecho se ha observado superconductividad en sales orgánicas, pero hasta ahora solo a temperaturas de transición alrededor de un Kelvin: El sueño de Little aún no se ha realizado.

Teoría de la perturbación de segundo orden: un potencial periódico en una dimensión

Para entender cómo un conductor unidimensional podría convertirse en un aislante a bajas temperaturas, primero debemos familiarizarnos con el modelo más simple de un conductor unidimensional:

\[ H=H^0+V=\frac{p^2}{2m}+V(x) \label{9.2.1}\]

con\(H^0\) un gas de electrones que no interactúan en una línea, y\(V\) periódico, es decir\(V(x+a)=V(x)\),

el potencial de una línea de iones\(a\) separados. Tomaremos el sistema para que tenga\(N\) iones en una longitud total\(L\), así

\[ L=Na \label{9.2.2}\]

y para mantener la matemática simple, vamos a requerir condiciones de límite periódicas.

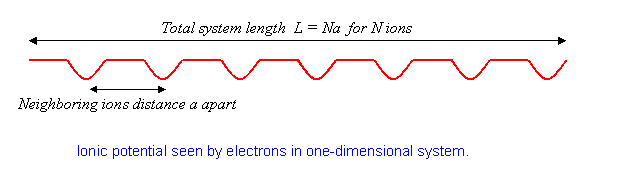
La física aquí es que sin el potencial, los estados propios de electrones son ondas planas. El efecto del potencial reticular es reflejar parcialmente las ondas, como una rejilla de difracción, generando componentes a diferentes longitudes de onda. Este efecto se vuelve particularmente importante cuando la longitud de onda del electrón coincide con el doble del espaciado iónico Para ese caso, las ondas reflejadas y originales tienen la misma fuerza, el electrón se encuentra paralizado. Exploraremos cómo sucede esto más adelante.

Los autoestados de\(H^0\) son entonces\[ |k\rangle^{(0)}=\frac{1}{\sqrt{L}}e^{ikx}, \;\; with\;\; e^{ikL}=1, \;\; so\;\; k=\frac{2\pi n}{L}, \label{9.2.2B}\]

\(n\)siendo un entero. Los imperturbables valores propios de la energía,\[ H^0|k\rangle^{(0)}  =E^0|k\rangle^{(0)},\; are\; just\; E^0=\frac{\hbar^2k^2}{2m}. \label{9.2.3}\]

Esto debe entenderse como

\[ H^0|k_n\rangle^{(0)}  =E^0_n|k_n\rangle^{(0)}\label{9.2.4A}\]

\[E^0_n=\frac{\hbar^2k_n^2}{2m}\label{9.2.4B}\]

y

\[k_n=2\pi nL. \label{9.2.4C}\]

Estamos siguiendo la práctica estándar aquí. También escribiremos\(\sum_k f(k)\) significado\(\sum_n f(k_n)\).)

Vale la pena trazar la\((E, k)\) curva:

Supongamos que tenemos iones con dos electrones cada uno para contribuir a este conductor unidimensional (supuesto). Suponiendo que se muevan a estos estados de onda plana, en el estado base del sistema llenarán los estados de energía más bajos hasta un valor k- máximo denotado por\(\pm k_F\) (\(F\)significa Fermi, este es el impulso de Fermi). ¿Dónde está?

Sabemos que habrá un total de\(2N\) electrones. También sabemos que los valores permitidos de\(k\), a partir de las condiciones de contorno, son\(k_n=2\pi n/L\), con\(n\) un entero. En otras palabras, los permitidos\(k\) están uniformemente\(2\pi /L\) espaciados, lo que significa que tienen una densidad de\(L/2\pi\) en k- espacio, por lo que el número total entre\(\pm k_F\) es\(Lk_F/\pi\). \(2N\)Los electrones tendrán\(N\) de cada espín, cada estado k puede tomar dos electrones (uno de cada espín), así\(Lk_F/\pi =N=L/a\), y\[ k_F=\pi /a. \label{9.2.5}\]

Para hacer teoría de perturbación, debemos encontrar los elementos matriciales de\(V(x)\) entre estados propios de\(H^0\):

\[ ^{(0)}\langle k′|V|k\rangle^{(0)}=1L\int ei(k-k')xV(x)dx. \label{9.2.5B}\]

Este es solo el componente de Fourier\(V_{k-k′}\) de\(V(x)\).

Si\(V(x)\) es periódico con periodo\(a\),\[ V_k\neq 0 \;\; only\; if\;\; k=nK,\;\; n\; an\; integer,\;\; K=2\pi /a. \label{9.2.6}\]

En otras palabras, si una función es periódica con periodo espacial\(a\), los únicos componentes de Fourier distintos de cero son aquellos que tienen el mismo periodo espacial\(a\).

Por lo tanto\[ V(x)=\sum_n V_{nK}e^{inKx},\;\; and\;\; V_{-nK}=V^∗_{nK}\;\; since\; V(x)\; is\; real;\;\; K=2\pi /a. \label{9.2.7}\]

El\(n=0\) componente de\(V(x)\) no tiene interés, es solo un potencial constante, y así se puede tomar como cero. Tenga en cuenta que esto elimina la corrección trivial de primer orden\(E^1_k=  ^{(0)}\langle k|V|k\rangle^{(0)}\) a los valores propios de energía.

Consideraremos únicamente los componentes\(n=+1\) y\(n=-1\) de\(V(x)\), resulta que los demás componentes pueden ser tratados de manera similar. Para\(n=+1\),\(n=-1\), el potencial solo tiene elementos de matriz distintos de cero entre el estado de onda plana\(k\) y\(k+K\),\(k-K\) respectivamente.

Entonces, la corrección de segundo orden a la energía es:\[ \begin{matrix} E^2_k=\sum_{k′\neq k} \frac{| ^{(0)}\langle k|V|k′\rangle^{(0)}|^2}{E^0_k-E^0_{k′}} \\ =\frac{| ^{(0)}\langle k|V|k+K\rangle^{(0)}|^2}{E^0_k-E^0_{k+K}}+\frac{| ^{(0)}\langle k|V|k-K\rangle^{(0)}|^2}{E^0_k-E^0_{k-K}} \\ =\frac{|V_K|^2}{E^0_k-E^0_{k+K}}+\frac{|V_{-K}|^2}{E^0_k-E^0_{k-K}}. \end{matrix} \label{9.2.8}\]

Este resultado es razonable siempre que los términos sean pequeños, es decir, las diferencias de energía que aparecen en los denominadores son grandes en comparación con el componente relevante de Fourier\(V_K\). Sin embargo, ¡esto no siempre puede ser cierto! Observe que el estado\(k=\pi /a\) tiene exactamente la\(E^0\) misma energía imperturbable que el estado\(k-K=-\pi /a\): en este caso, la teoría de la perturbación no degenerada está claramente equivocada. De hecho, incluso para estados cercanos a\(k=\pi /a\), el denominador energético\(E^0_k-E^0_{k-K}\) es pequeño comparado con el numerador\(|V_{-K}|^2\), por lo que la serie no está convergiendo.

Teoría de perturbación cuasi-degenerada cerca de la longitud de onda crítica

La buena noticia es que, a pesar de los muchos estados cercanos\(k=\pi /a\) y\(k=-\pi /a\) que están muy juntos en energía, para cualquier estado\(k\) cercano\(\pi /a\) al potencial sólo tiene un elemento matriz distinto de cero a otro estado cercano en energía, el estado\(k-K\), es decir,\(k-2\pi /a\).

La estrategia ahora es hacer lo que podría llamarse teoría de perturbación cuasidegenerar: diagonalizar lo hamiltoniano completo en el subespacio abarcado por estos dos estados\(|k\rangle^{(0)},\;  |k-K\rangle^{(0)}\). Otros estados con elementos de matriz distintos de cero a estos estados están relativamente mucho más alejados en energía, y pueden tratarse usando la teoría de perturbación ordinaria.

Los elementos matriciales del Hamiltoniano completo en el subespacio abarcados por estos dos estados son:\[ \begin{vmatrix} E^0_k &V^∗_K \\ V^*_K &E^0_{k-K} \end{vmatrix}. \label{9.2.9}\]

La diagonalización dentro de este subespacio da valores propios de energía:

\[ E_{\pm} =\frac{1}{2}(E^0_k+E^0_{k-K})\pm \sqrt{\left( \frac{E^0_k-E^0_{k-K}}{2}\right)^2+|V_K|^2}. \label{9.2.10}\]

Observe que, siempre que\(|E^0_k-E^0_{k-K}|\gg |V_K|\), al orden principal esto devuelva\(E_{\pm} =E^0_k, \; E^0_{k-K}\), el orden dependiendo de\(k\). Sin embargo, a medida que se\(k\)\(\pi /a\) aproxima\(|V_K|\),\(|E^0_k-E^0_{k-K}|\) se vuelve de orden, y las energías se desvían de los valores imperturbables. Si\(k\) se acerca\(\pi /a\) desde abajo,\(E^0_k<E^0_{k-K}\), y la energía inferior es empujada hacia abajo por la perturbación:\(E_k=E_-<E^0_k\). Esta es una ocurrencia común con estados casi degenerados, las perturbaciones hacen que los niveles de energía se “repelan” entre sí.

Para\(k=\pi /a,\; E^0_{k-K}=E^0_{k-2\pi /a}=E^0_k\). A este valor de\(k\), los estados imperturbables son exactamente degenerados, y la perturbación levanta la degeneración para dar\(E_{\pm} =E^0_{\pi /a}\pm |V_K|\).

En la gráfica siguiente, la curva verde (continua) es la energía no perturbada en función de\(k\), la curva roja (con el paso) la energía calculada incluyendo la corrección inicial del potencial periódico.

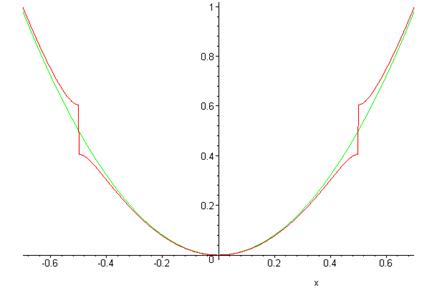
Brechas y bandas de energía

El salto de energía, o brecha, de\(2|V_K|\) at\(|k|=\pi/a\) significa que no hay estados propios del tipo de onda plana con energías en ese rango; intentar integrar la ecuación de Schrödinger en el potencial periódico para tal energía da soluciones exponencialmente crecientes y en descomposición. Tales brechas de energía de hecho están presentes en sólidos cristalinos reales, se dice que las energías permitidas están en “bandas”. La banda más baja para nuestro modelo es de\(k=-\pi/a\) a\(\pi/a\). Dado que los valores permitidos de\(k\) están dados por\(k=2\pi n/L\), el espaciamiento entre los adyacentes\(k\) es\(2\pi/L\) y el número total\(k\) de s en la banda más baja es\(L/a=N\), el mismo que el número de átomos. Dado que cada electrón tiene dos estados de espín, esto implica que un cristal unidimensional de átomos divalentes simplemente llenará la banda más baja con electrones. Por lo tanto, cualquier campo exterior solo puede excitar un electrón a un estado diferente si\(2|V_K|\) se suministra una energía de al menos, para un campo eléctrico pequeño, la banda llena de electrones permanecerá en el estado fundamental, no habrá corriente. Este material es un aislante.

Por otro lado, si se utilizan átomos monovalentes, es claro que la banda más baja es solo la mitad llena, los estados de electrones vacíos adyacentes están disponibles. Los electrones son libres de acelerar si se aplica un campo externo. Salvo lo inesperado, este cristal unidimensional sería un metal.

Examinemos ahora cómo el potencial periódico altera los autoestados. Ignorando las pequeñas correcciones de ondas planas fuera del\(|k\rangle^{(0)},\;  |k-K\rangle^{(0)}\) subespacio, los autoestados a este orden tienen la forma\[ |k\rangle=a_k|k\rangle^{(0)}+a_{k-K}|k-K\rangle^{(0)} \label{9.2.11}\]

donde\[ \frac{a_{k-K}}{a_k}=\frac{E_--E^0_k}{V^∗_K} \label{9.2.12}\]

a partir de la diagonalización de la\(2\times 2\) matriz que representa al hamiltoniano en el subespacio.

A\(k\) medida que aumenta de 0 hacia\(\pi/a\), la onda plana inicialmente proporcional a\(e^{ikx}\) tiene una mezcla gradualmente creciente de\(e^{i(k-2\pi/a)x}\), hasta que en\(k=\pi/a\) los dos tienen el mismo peso, lo que significa que la función propia es ahora una onda estacionaria. De hecho, hay dos soluciones de onda estacionaria en\(k=\pi/a\), correspondientes a las energías por debajo y por encima de la brecha. Tomando los átomos para tener un potencial atractivo, la onda de menor energía tiene una distribución de probabilidad que alcanza su punto máximo en las posiciones atómicas. La dispersión difractiva que da un componente que se mueve hacia la izquierda a una onda en movimiento derecho se conoce como dispersión de Bragg. También se manifiesta en la velocidad grupal de las excitaciones electrónicas,\(v_{group}=d\omega/dk=(1/\hbar)dE/dk\). Un electrón inyectado en un metal unidimensional no sería un estado de onda plana, sino un paquete de ondas viajando a la velocidad del grupo. Es evidente que para un electrón inyectado con valor medio\(k\) cercano a\(\pi/a\), el electrón se moverá muy lentamente hacia el metal. Esto es de esperar—los propios estados se convierten en ondas estacionarias como\(k\to \pi/a\).

Para los cristales tridimensionales, la situación es mucho más complicada, pero muchas de las mismas ideas son relevantes. Las ondas de electrones ahora son difractadas por planos enteros de átomos, y el espacio de impulso tridimensional se divide en zonas Brillouin, con planos que tienen una brecha de energía a través de ellas.

La transición de Peierls: cómo enfriar un conductor puede dar un aislante

Como se menciona en la Introducción, se han sintetizado sustancias muy cercanas a los cristales monovalentes unidimensionales, y se ha encontrado, de manera sorpresiva, que a bajas temperaturas muchos de ellos experimentan una transición del comportamiento metálico al aislante. Lo que sucede es que los átomos en la celosía se reordenan ligeramente, pasando de un cristal igualmente espaciado a uno en el que se alterna el espaciamiento, es decir, los átomos forman pares. Esto se llama dimerización, y cuesta algo de energía elástica, ya que para átomos idénticos el estado más bajo debe ser uno de igual espaciamiento para cualquier potencial razonable. Sin embargo, los electrones son capaces de moverse a un estado de menor energía mediante esta maniobra.

Justo cómo sucede esto se puede entender utilizando el análisis de la teoría de perturbaciones anterior. Para átomos igualmente espaciados, los electrones llenan la mitad de la banda, es decir, la llenan (dos electrones, uno de cada espín, por estado) a\(|k|=\pi/2a\).

El punto crucial es que si los átomos se mueven juntos ligeramente en pares, el cristal tiene un nuevo período\(2a\) en lugar de\(a\). Esto significa que el potencial ahora tiene un componente distinto de cero en\(K=-\pi/a\), con un elemento de matriz distinto de cero entre los estados\(k=\pi/2a\) y\(k=-\pi/2a\), y así sucesivamente. A partir de este punto, podemos volver a ejecutar el análisis anterior, salvo que ahora las brechas se abren en\(|k|=\pi/2a\) lugar de en\(|k|=\pi/a\).

El punto importante es que si los electrones llenan todos los estados hasta\(|k|=\pi/2a\), y ninguno más allá (como sería el caso de los átomos monovalentes) entonces la apertura de un hueco en\(|k|=\pi/2a\) significa que todos los electrones están en estados cuya energía se baja. Para encontrar el beneficio energético total necesitamos integrarnos sobre\(k\).

Cálculo de la energía electrónica ganada al duplicar el período de celosía

Es evidente de lo anterior que la mayor parte de la contribución proviene de bastante cerca\(k=\pi/2a\) (y por supuesto simétricamente\(k=-\pi/2a\)). Como queremos encontrar la disminución total de la energía, estudiemos primero la energía desnuda en función de\(k\), es decir, la energía sin potencial presente. Por supuesto, no hay mucho que decir:\(E^0_k=\hbar^2k^2/2m\). Sin embargo, la física de estos sistemas unidimensionales se refiere solo a las excitaciones cercanas a la “superficie Fermi”, el límite entre estados llenos (baja energía) a temperatura cero y estados vacíos. Esta “superficie Fermi” es de hecho solo dos puntos en una dimensión:\(k=\pm  \pi/2a\). En el barrio de estos dos puntos Fermi, es una excelente aproximación para reemplazar el curvar suavemente\(E^0_k=\hbar^2k^2/2m\) por aproximaciones en línea recta —siendo la pendiente\(dE/dk=\hbar^2k/m=\hbar p/m=\hbar v.\)

Linealizar en el barrio de\(k=\pi/2a\), entonces, tomamos

\[ E^0_k=E^0_{\pi/2a}+\hbar v(k-\pi/2a)=E^0_{\pi/2a}+\hbar vq, \label{9.2.13}\]

donde

\[ q=k-\pi/2a,\label{9.2.14}\]

apenas k medido desde el punto Fermi\(\pi/2a\).

La variable\(q\) es negativa para los estados relevantes, ya que están en el lado de menor energía.

La densidad de estados en el espacio k es una constante\(2\times L/2\pi =L/\pi\), recordando los dos estados de giro por valor k-.

Recordar

\[ E_{\pm} =\dfrac{1}{2}(E^0_k+E^0_{k-K})\pm \sqrt{\left( \frac{E^0_k-E^0_{k-K}}{2}\right)^2+|V_K|^2} \label{9.2.10B}\]

pero ahora

\[ K=\pi/a \label{9.2.15}\]

y la disminución de la energía de los electrones (contándola como una cantidad positiva) es:

\[ 2\int_0^{\pi/2a} (E^0_k-E_-)Ldk/\pi =2\int \left( \frac{1}{2}(E^0_k-E^0_{k-K})+\sqrt{\left( \frac{E^0_k-E^0_{k-K}}{2}\right)^2+|V_K|^2}\right)  Ldk/\pi \label{9.2.16}\]

donde el factor extra de 2 cuenta la contribución simétrica de la brecha izquierda. (Al examinar la expresión anterior, recordemos que para los\(k>0\) estados que nos interesan,\(k<\pi/2a,\; E^0_k-E^0_{k-K}\) es negativo. El integrando del lado derecho sigue siendo positivo, muy pequeño para k pequeño, alcanzando un máximo de\(|V_K|\) at\(k=\pi/2a\).)

Poniendo en nuestra aproximación linealizada de energía,

\[ E^0_k=E^0_{\pi/2a}+\hbar v(k-\pi/2a)=E^0_{\pi/2a}+\hbar vq, \label{9.2.17}\]

y recordando que ahora\(K=\pi/a\),

\[ E^0_{k-K}=E^0_{-\pi/2a}-\hbar v(k+\pi/2a)=E^0_{-\pi/2a}-\hbar vq. \label{9.2.18}\]

Dado que\(E^0_{\pi/2a}=E^0_{-\pi/2a}\),\[ (E^0_k-E^0_{k-K})=2v\hbar q. \label{9.2.19}\]

Sustituyendo estos valores linealizados en la integral por la disminución total de la energía:

\[ 2\int_0^{\pi/2a}(E^0_k-E_-)Ldk/\pi =2\int_{-D}^0(v\hbar q+ \sqrt{(v\hbar q)^2+|V_K|^2})Ldq/\pi \label{9.2.20}\]

donde en términos de la variable\(q\) hemos establecido el límite inferior de integración en\(-D\): podemos ser vagos con seguridad sobre este límite inferior, ya que la integral resulta ser logarítmica.

Dado que la integral está por encima de números negativos, y hemos tomado la raíz cuadrada positiva, es cero para cero\(V_K\), como debe ser.

La integral se puede hacer exactamente, pero es más esclarecedor dividir el rango de integración en\(|v\hbar q|\le |V_K|\) y\(|v\hbar q|> |V_K|\), luego estimar las contribuciones de estos dos rangos por separado.

Primero, considere\(|v\hbar q|\le  |V_K|\). Aquí el integrando es de orden\(|V_K|\), y la región\(\Delta q\) de integración correspondiente a\(|v\hbar q|\le  |V_K|\) es de orden\(|V_K|/\hbar v\), por lo que la integral sobre este rango es de orden\((L/\hbar v)|V_K|^2\).

Segundo, en la región\(|v\hbar q|> |V_K|\), podemos escribir

\[ 2\int (v\hbar q+\sqrt{(v\hbar q)^2+|V_K|^2})  Ldq/\pi = 2\int \left( v\hbar q+|v\hbar q|\sqrt{1+\frac{|V_K|^2}{(v\hbar q)^2}}\right) Ldq/\pi \label{9.2.21}\]

y ampliar el término raíz cuadrada. Los términos principales cancelan ya que\(q\) es negativo, y la contribución principal proviene del siguiente término. Esto da:

\[ \Delta E\approx 2|V_K|^2\int_{-D}^{-|V_K|} \dfrac{1}{2\hbar v}\frac{Ldq}{\pi |q|} =\dfrac{L|V_K|^2}{\hbar v} \ln \dfrac{|V_K|}{D}. \label{9.2.22}\]

Lo importante aquí es el logaritmo. Por suficientemente pequeño\(|V_K|\), este término grande (negativo) dominará cualquier término que sea apenas proporcional a\(V^2_K\). Pero el costo de energía elástica de la red “dimerizante” —los átomos que forman pares, de manera que la distancia entre los átomos se alterna al ir a lo largo de la cadena— debe ser proporcional a\(V^2_K\). Esto lleva a la conclusión de que siempre va a ocurrir alguna dimerización, probablemente pequeña; una cadena unidimensional igualmente espaciada con un electrón por ion es inestable.

Esta dimerización se conoce como una transición de Peierls. Peierls lo descubrió en la década de 1930 al escribir una sección sobre modelos unidimensionales en un libro de texto introductorio de estado sólido. Lo puso en el libro, pero no lo publicó de otra manera. Como se mencionó en la Introducción, se volvió muy relevante más tarde cuando algunas teorías sugirieron que los conductores cuasi-unidimensionales, materiales compuestos por cadenas sueltas conectadas, teniendo cada cadena un electrón por átomo para una banda más baja medio llena, podrían ser superconductores de alta temperatura. Se encontró en cambio que muchos de esos materiales en realidad se convirtieron en aislantes al enfriarse: la razón fue que a altas temperaturas, los electrones llenaron estados por encima y por debajo del punto de\(\pi/2a\) manera bastante igual, por lo que la dimerización no bajó mucho la energía general. Al bajar la temperatura, se alcanzó un punto donde la transición de los Peierls dio un estado energético más bajo, y el material se convirtió en aislante.