13.1: Teorema de Bell

INTRODUCCIÓN

En 1975 Stapp calificó al Teorema de Bell “el descubrimiento más profundo de la ciencia”. Tenga en cuenta que dice ciencia, no física. Estoy de acuerdo con él.

En este documento, exploraremos el teorema. Asumimos cierta familiaridad con el concepto de dualidad onda-partícula. También asumimos una considerable familiaridad con el experimento de Stern-Gerlach y el concepto de experimento de correlación.

html

pdf

Se ha preparado una introducción mucho más sencilla al teorema, con cierta pérdida de integridad. Puede acceder a una versión html o pdf con los enlaces a la derecha.

El origen de este tema es un famoso artículo de Einstein, Rosen y Podolsky (EPR) en 1935; su título fue ¿Puede considerarse completa la descripción cuántico-mecánica de la realidad física? Consideraron lo que Einstein llamó la “acción espeluznante a distancia” que parece ser parte de la Mecánica Cuántica, y concluyeron que la teoría debe estar incompleta si no completamente equivocada. Como probablemente ya sabrás, Einstein nunca aceptó la Mecánica Cuántica. Una de sus objeciones fue que “Dios no juega a los dados con el universo”. Bohr respondió: “¡Deja de decirle a Dios qué hacer!”

A principios de la década de 1950, David Bohm (no “Bohr”) era un joven profesor de Física en la Universidad de Princeton. Fue asignado para enseñar Mecánica Cuántica y, como es común, decidió escribir un libro de texto sobre el tema; el libro sigue siendo un clásico. Einstein estaba en Princeton en este momento, y como Bohm terminaba cada capítulo del libro Einstein lo criticaría. Para cuando Bohm había terminado el libro Einstein le había convencido de que la Mecánica Cuántica estaba al menos incompleta. Bohm pasó entonces muchos años en busca de variables ocultas, factores no observados dentro, digamos, de un átomo radiactivo que determina cuándo va a descomponerse. En una teoría de variables ocultas, el tiempo para que ocurra la decadencia no es aleatorio, aunque la variable que controla el proceso se nos oculta. Discutiremos ampliamente el trabajo de Bohm más adelante en este documento.

En 1964 J.S. Bell publicó su teorema. Fue lanzado en términos de una teoría de variables ocultas. Desde entonces, han aparecido otras pruebas de d'Espagnat, Stapp, y otras que no son en términos de variables ocultas. A continuación haremos una variación de la prueba de d'Espagnat que ideé; fue publicada originalmente en el American Journal of Physics 50, 811 - 816 (1982).

DEMOSTRANDO LA DESIGUALDAD DE BELL

Seremos un poco matemáticos. Los detalles de las matemáticas no son importantes, pero hay un par de piezas de la prueba que serán importantes. El resultado de la prueba será que para cualquier colección de objetos con tres parámetros diferentes, A, B y C:

El número de objetos que tienen el parámetro A pero no el parámetro B más el número de objetos que tienen el parámetro B pero no el parámetro C es mayor o igual que el número de objetos que tienen el parámetro A pero no el parámetro C.

Podemos escribir esto de manera más compacta como:

Número (A, no B) + Número (B, no C) mayor o igual que Número (A, no C)

A la relación se le llama desigualdad de Bell.

En clase a menudo hago a los alumnos la colección de objetos y elijo los parámetros para ser:

A: macho B: altura sobre 5' 8" (173 cm) C: ojos azules

Entonces la desigualdad se convierte en que el número de estudiantes varones que no tienen una estatura superior a 5' 8" más el número de estudiantes, hombres y mujeres, con una altura superior a 5' 8" pero que no tienen ojos azules es mayor o igual al número de estudiantes varones que no tienen ojos azules. Garantizo absolutamente que para cualquier colección de personas esto va a resultar cierto.

Es importante destacar que no estamos haciendo ninguna suposición estadística: la clase puede ser grande, pequeña o incluso de tamaño cero. Además, no estamos asumiendo que los parámetros sean independientes: tenga en cuenta que tiende a haber una correlación entre género y estatura.

A veces la gente tiene problemas con el teorema porque vamos a estar haciendo una variación de una técnica llamada prueba por negación. Por ejemplo, aquí hay un silogismo:

Todas las arañas tienen seis patas. Todas las criaturas de seis patas tienen alas. Por lo tanto todas las arañas tienen alas

Si alguna vez observamos una araña que no tiene alas, entonces sabemos que al menos una y posiblemente ambas suposiciones del silogismo son incorrectas. De igual manera, derivaremos la desigualdad y luego mostraremos una circunstancia experimental donde no es cierta. Así sabremos que al menos uno de los supuestos que utilizamos en la derivación es erróneo.

Además, veremos que la prueba y sus pruebas experimentales no tienen absolutamente nada que ver con la Mecánica Cuántica.

Ahora estamos listos para la prueba misma. Primero, afirmo que:

Número (A, no B, C) + Número (no A, B, no C) debe ser 0 o un entero positivo

o equivalentemente:

Número (A, no B, C) + Número (no A, B, no C) mayor o igual a 0

Esto debería ser bastante obvio, ya que o ningún miembro del grupo tiene estas combinaciones de propiedades o algunos miembros sí.

Ahora agregamos Número (A, no B, no C) + Número (A, B, no C) a la expresión anterior. El lado izquierdo es:

Número (A, no B, C) + Número (A, no B, no C) + Número (no A, B, no C) + Número (A, B, no C)

y el lado derecho es:

0 + Número (A, no B, no C) + Número (A, B, no C)

Pero este lado derecho es solo:

Número (A, no C)

ya que para todos los miembros ya sea B o no B debe ser cierto. En el ejemplo de aula anterior, cuando contamos el número de hombres sin ojos azules incluimos tanto a aquellos cuya estatura era superior a 5' 8" como a aquellos cuya altura no era superior a 5' 8".

Arriba escribimos “ya que para todos los miembros ya sea B o no B debe ser cierto”. Esto resultará importante.

De manera similar podemos recopilar términos y escribir el lado izquierdo como:

Número (A, no B) + Número (B, no C)

Desde que iniciamos la prueba afirmando que el lado izquierdo es mayor o igual que el lado derecho, hemos demostrado la desigualdad, que vuelvo a declarar:

Número (A, no B) + Número (B, no C) mayor o igual que Número (A, no C)

Hemos hecho dos suposiciones en la prueba. Estos son:

• La lógica es una forma válida de razonar. Toda la prueba es un ejercicio de lógica, aproximadamente al nivel de los acertijos de “Diversión con números” que a veces se ve en periódicos y revistas.
• Los parámetros existen tanto si se miden como si no. Por ejemplo, cuando recogimos los términos Número (A, no B, no C) + Número (A, B, no C) para obtener Número (A, no C), asumimos que o no B o B es cierto para cada miembro.

APLICAR LA DESIGUALDAD DE BELL AL ESPÍN ELECTRÓNICO

Considera un haz de electrones de un cañón de electrones. Establezcamos las siguientes asignaciones para los tres parámetros de la desigualdad de Bell:

R: los electrones son “spin-up” para un “arriba” que se define como recto hacia arriba, lo que llamaremos un ángulo de cero grados. B: los electrones son “spin-up” para una orientación de 45 grados. C: los electrones son “spin-up” para una orientación de 90 grados.

Entonces la desigualdad de Bell leerá:

Número (spin-up cero grados, no spin-up 45 grados) + Número (spin up 45 grados, no spin-up 90 grados) mayor o igual a Número (spin up cero grados, no spin up 90 grados)

Pero considere tratar de medir, digamos, Número (A, no B). Este es el número de electrones que son spin-up para cero grados, pero no son spin-up para 45 grados. Ser “no spin-up por 45 grados” es, por supuesto, ser spin- down por 45 grados.

Sabemos que si medimos los electrones del cañón, la mitad de ellos serán spin-up y la mitad será spin-down para una orientación de 0 grados, y que será el caso de un electrón individual es aleatorio. De igual manera, si se miden los electrones con el filtro orientado a 45 grados, la mitad será spin-down y la mitad será spin-up.

Pero si tratamos de medir el giro tanto a 0 grados como a 45 grados tenemos un problema.

La figura de la derecha muestra una medición primero a 0 grados y luego a 45 grados. De los electrones que emergen del primer filtro, 85% pasará por el segundo filtro, no 50%. Así, para los electrones que se miden para ser spin-up para 0 grados, 15% son spin-down para 45 grados.

Por lo tanto, medir el espín de un electrón en un ángulo de cero grados cambia irrevocablemente el número de electrones que son spin-down para una orientación de 45 grados. Si medimos primero a 45 grados, cambiamos si es o no spin-up por cero grados. De igual manera para los otros dos términos en esta aplicación de la desigualdad. Esto es consecuencia del Principio de Incertidumbre de Heisenberg. Entonces esta desigualdad no es experimentalmente comprobable.

En nuestro ejemplo de aula, la analogía sería que determinar el género de los alumnos cambiaría su estatura. Bastante raro, pero cierto para medir el espín de electrones.

Sin embargo, recordemos los experimentos de correlación que discutimos anteriormente. Imagínese que los pares de electrones que son emitidos por la sustancia radiactiva tienen un espín total de cero. Con esto queremos decir que si el electrón de la derecha es spin-up su electrón compañero está garantizado para ser spin-down siempre que los dos filtros tengan la misma orientación.

Digamos que en el experimento ilustrado el filtro de la izquierda está orientado a 45 grados y el de la derecha está a cero grados. Si el electrón de la izquierda pasa a través de su filtro entonces es girado hacia arriba para una orientación de 45 grados. Por lo tanto, se nos garantiza que si hubiéramos medido su electrón compañero habría sido spin-down para una orientación de 45 grados. Simultáneamente estamos midiendo el electrón de la derecha para determinar si es spin-up para cero grados. Y dado que ninguna información puede viajar más rápido que la velocidad de la luz, la medición de la mano izquierda no puede alterar la medición de la mano derecha.

Entonces hemos “batido” el Principio de Incertidumbre: hemos determinado si el electrón a la derecha es o no spin-up cero grados, no spin-up 45 grados midiendo su giro a cero grados y el giro de su compañero a 45 grados.

Ahora podemos escribir la desigualdad de Bell como:

Número (giro derecho cero grados, giro izquierdo 45 grados) + Número (giro derecho 45 grados, giro izquierdo 90 grados) mayor o igual a Número (giro derecho cero grados, giro izquierdo 90 grados)

Esto completa nuestra prueba del teorema de Bell.

El mismo teorema se puede aplicar a las mediciones de la polarización de la luz, lo que equivale a medir el espín de pares de fotones.

Se han realizado los experimentos. Para los electrones el polarizador izquierdo se fija a 45 grados y el derecho a cero grados. Se mide un haz de, digamos, mil millones de electrones para determinar el Número (giro derecho cero grados, giro izquierdo 45 grados). Los polarizadores se fijan entonces en 90 grados/45 grados, se miden otros mil millones de electrones, luego los polarizadores se fijan en 90 grados/cero grados para otros mil millones de electrones.

El resultado del experimento es que se viola la desigualdad. El primer experimento publicado fue por Clauser, Horne, Shimony y Holt en 1969 utilizando pares de fotones. Los experimentos se han repetido muchas veces desde entonces.

Los experimentos realizados hasta ahora han sido para pares de electrones, protones, fotones y átomos ionizados. Resulta que hacer los experimentos para pares de fotones es más fácil, por lo que la mayoría de las pruebas los utilizan. Así, en la mayor parte del resto de este documento la palabra “electrón” es genérica.

Nota técnica: Puede recordar de nuestra discusión del experimento de Stern-Gerlach que hacer un experimento de correlación para electrones con los polarizadores en algún ángulo relativo equivale a hacer el experimento para fotones con los polarizadores a la mitad del ángulo relativo de los polarizadores de electrones. Así, cuando discutimos una medición de electrones con los polarizadores a, digamos, cero grados y 45 grados, para un experimento de fotones sería cero grados y 22.5 grados.

En la última sección hicimos dos supuestos para derivar la desigualdad de Bell que aquí se convierten en:

• La lógica es válida.
• Los electrones tienen giro en una dirección dada aunque no lo medimos.

Ahora hemos sumado una tercera suposición para vencer al Principio de Incertidumbre:

• Ninguna información puede viajar más rápido que la velocidad de la luz.

Los expondremos un poco más sucintamente como:

1. La lógica es válida.
2. Hay una realidad separada de su observación
3. Localidad.

Recordarás las pruebas que discutimos por negación. El hecho de que nuestra forma final de desigualdad de Bell sea violada experimentalmente indica que al menos uno de los tres supuestos que hemos hecho se ha demostrado que está equivocado.

También recordarán que antes señalamos que el teorema y sus pruebas experimentales no tienen nada que ver con la Mecánica Cuántica. Sin embargo, el hecho de que la Mecánica Cuántica prediga correctamente las correlaciones que se observan experimentalmente indica que la teoría también viola al menos uno de los tres supuestos.

Finalmente, como dijimos, la prueba original de Bell fue en términos de teorías de variables ocultas. Sus suposiciones fueron:

1. La lógica es válida.
2. Existen variables ocultas.
3. Las variables ocultas son locales.

La mayoría de la gente, incluyéndome a mí, ve el supuesto de variables ocultas locales como muy similar al supuesto de una realidad local.

¿Y AHORA QUÉ?

Como se puede imaginar fácilmente, mucha gente ha tratado de salirse de este profundo resultado. Algunos intentos han criticado las pruebas experimentales. Un argumento es que como establecemos los dos polarizadores en algún conjunto de ángulos y luego recolectamos datos para, digamos, mil millones de electrones hay tiempo suficiente para que los polarizadores se “conozcan” la orientación del otro, aunque no por ningún mecanismo conocido. Pruebas más recientes establecen la orientación de los polarizadores aleatoriamente después de que los electrones hayan salido de la fuente. Los resultados de estas pruebas son los mismos que los experimentos anteriores: se viola la desigualdad de Bell y se confirman las correlaciones cuánticas predichas. Aún otras pruebas han establecido la distancia entre los dos polarizadores en 11 km, con resultados que confirman nuevamente las correlaciones cuánticas.

Otra crítica ha sido que dado que los pares correlacionados emitidos por la fuente van en todas direcciones, solo una fracción muy pequeña de ellos en realidad terminan siendo medidos por los polarizadores. Otro experimento que utilizó átomos de berilio correlacionados midió casi todos los pares, con resultados nuevamente confirmaron las correlaciones cuánticas.

Hay otra objeción a las pruebas experimentales que, al menos hasta ahora, nadie ha logrado moverse totalmente. Medimos una combinación de espín de, digamos, cero grados y 45 grados para una colección de electrones y luego medimos otra combinación de espín, digamos 45 grados y 90 grados, para otra colección de electrones. En nuestro ejemplo de aula, esto es como medir el número de estudiantes varones cuya estatura no es superior a 5' 8" en una clase, y luego usar otra clase de estudiantes diferentes para medir el número de estudiantes cuya estatura es superior a 5' 8" pero no tienen ojos azules. La diferencia es que una colección de, digamos, mil millones de electrones de la fuente en los experimentos de correlación siempre se comporta de manera idéntica dentro de pequeñas y esperadas fluctuaciones estadísticas con cualquier otra colección de mil millones de electrones de la fuente. Dado que ese hecho ha sido verificado muchas veces para todos los experimentos de todo tipo, asumimos que es cierto cuando estamos haciendo estos experimentos de correlación. Esta suposición es un ejemplo de lógica inductiva; por supuesto que asumimos la validez de la lógica en nuestra derivación.

A veces se ven declaraciones de que el Teorema de Bell dice que la información se está transmitiendo a velocidades mayores que la velocidad de la luz. Hasta el momento no he visto tal argumento que creo que sea correcto. Si estamos sentados junto a cualquiera de los polarizadores vemos que la mitad de los electrones pasan y la mitad no; que va a ser el caso de un electrón individual parece ser aleatorio. Así, el comportamiento en nuestro polarizador no nos permite obtener ninguna información sobre la orientación del otro polarizador. Es sólo en la correlación de los espines electrónicos que vemos algo extraño. d'Espagnat usa la palabra influencia para describir lo que puede estar viajando a velocidades superluminales.

Imagina que tomamos una moneda y la vimos cuidadosamente por la mitad para que una pieza sea una “cabeza” y la otra sea una “cola”. Ponemos cada mitad en un sobre separado y los llevamos a diferentes habitaciones. Si abrimos uno de los sobres y vemos una cabeza, sabemos que el otro sobre contiene una cola. Este “experimento” de correlación corresponde a mediciones de espín cuando ambos polarizadores tienen la misma orientación. Es cuando tenemos los polarizadores en diferentes orientaciones que vemos algo raro.

Hasta el momento no sabemos cuáles de los supuestos que hicimos en la prueba son incorrectos, por lo que somos libres de elegir uno, dos o los tres. Cerraremos esta sección considerando brevemente las consecuencias de descartar el supuesto de validez de la lógica y luego las consecuencias de descartar el supuesto de una realidad separada de su observación. En la siguiente sección exploraremos la idea de un universo no local.

¿Qué pasa si la lógica no es válida?

Se sospecha desde mucho antes de Bell que la Mecánica Cuántica está en conflicto con la lógica clásica. Por ejemplo, la lógica deductiva se basa en una serie de supuestos, uno de los cuales es el Principio del Medio Excluido: todas las declaraciones son verdaderas o falsas.

Pero considere la siguiente pregunta de prueba de opción múltiple:

1. El electrón es una onda.
2. El electrón es una partícula.
3. Todo lo anterior.
4. Ninguna de las anteriores.

De la dualidad onda-partícula sabemos que ambas declaraciones 1 y 2 son tanto verdaderas como falsas. Esto parece poner en tela de juicio el Principio del Medio Excluido. Así, algunas personas han trabajado en una lógica multivalorada que esperan sea más consistente con las pruebas del Teorema de Bell y por tanto con la Mecánica Cuántica. The Dancing Wu Li Masters, de Gary Zukav, tiene una buena discusión de tal lógica cuántica; dado que existen numerosas ediciones de este libro y cada capítulo está numerado 0, no puedo proporcionar una referencia más detallada.

La matemática misma puede ser vista como solo una rama de la lógica deductiva, así que si revisamos las reglas de la lógica tendremos que idear una nueva matemática

Te puede interesar saber que la lógica deductiva ha demostrado que la lógica es incompleta. La prueba fue publicada en 1931 por Gödel; una buena referencia es Gödel, Escher, Bach de Hofstader. La clave de la obra de Gödel es la autorreferencia; veremos un ejemplo de autorreferencia en la siguiente subsección. Lo que demostró fue que cualquier matemática en absoluto, a menos que esté trivialmente limitada, contendrá afirmaciones que no son ni verdaderas ni falsas sino simplemente improbables.

Por autorreferencia nos referimos a una declaración o conjunto de afirmaciones que se refieren a sí mismas. Por ejemplo, considere: Esta afirmación es falsa. Tenga en cuenta que si esta afirmación es verdadera, entonces debe ser falsa. Si la declaración si es falsa, entonces debe ser verdadera. Entonces tenemos una cadena de Verdadero” Falso” Verdadero” Falso... .

New Yorker, 5 de marzo de 2001, pág. 78.

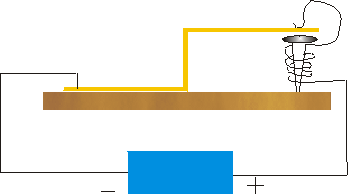Esto puede recordarle un poco a un timbre simple, como un timbre de puerta.

A la derecha se muestra un zumbador. Una pieza flexible de metal se dobla en forma de L doble y se clava a una tabla. Se coloca un clavo grande justo debajo de la parte derecha del metal, y el metal se ajusta para que no toque del todo el clavo grande. Una batería está cableada de tal manera que cuando el metal L está en reposo, el circuito acaba de completarse, lo que hace que el clavo grande se convierta en un electroimán.

Esto por supuesto tira el metal hacia abajo, lo que rompe el circuito. De esta manera los resortes metálicos vuelven a subir, lo que completa de nuevo el circuito, lo que tira del metal hacia abajo, y así sucesivamente. Así, si el circuito está cerrado, se abre, y si el circuito está abierto, entonces se cierra. O, decimos que tenemos una cadena de Cerrados” Abiertos” Cerrados” Abiertos... . La diferencia entre este ejemplo y la afirmación autorreferencial anterior es que aquí las oscilaciones de valor están ocurriendo en el tiempo. Puedes acceder a una animación Flash de un zumbador haciendo clic aquí.

A finales del siglo XIX el lógico Hilbert solía decir “La física es demasiado importante para dejarla en manos de los físicos”. En represalia, J.A. Wheeler ha declarado: “Gödel es demasiado importante para dejarlo en manos de los matemáticos”.

Por último, aunque la lógica deductiva se entiende bastante bien, nadie ha logrado codificar reglas férreas para la lógica inductiva que funcionen consistentemente. Mills se esforzó mucho por hacer esto, pero la siguiente historia de Copi muestra un problema:

“Un ejemplo favorito utilizado por los críticos del Método de Acuerdo es el caso del Bebedor Científico, a quien le gustaba muchísimo el licor y se emborrachaba todas las noches de la semana. Estaba arruinando su salud, y sus pocos amigos restantes le suplicaron que se detuviera. Al darse cuenta de que no podía continuar, resolvió realizar un cuidadoso experimento para descubrir la causa exacta de sus frecuentes embriagaciones. Durante cinco noches seguidas recolectó instancias de un fenómeno dado, siendo las circunstancias antecedentes respectivamente escocés y refresco, bourbon y refresco, brandy y refresco, ron y refresco, y ginebra y refresco [ugh!]. ¡Entonces usando el Método de Acuerdo juró solemne un juramento de no volver a tocar refresco nunca más!”

Referencia: I. Copi, Introducción a la lógica, 2a ed., (Macmillan, Nueva York, 1961), pp 394-395.

Anote la “variable oculta” en la historia anterior.

¿Y si no hay realidad separada de su observación?

Como hemos visto, el título de esta subsección es muy similar a preguntar cuáles son las consecuencias de no tener variables ocultas. Nos concentraremos en la primera forma de la cuestión.

Puede que ya hayas notado que la pregunta es una variación de la vieja sierra filosófica respecto a un árbol que cae en el bosque sin nadie ahí para escuchar el sonido.

Un conflicto entre la asunción de la realidad y la Mecánica Cuántica se ha sospechado mucho antes de Bell. Por ejemplo, al referirse a la trayectoria del electrón en, digamos, el experimento de doble rendija Heisenberg afirmó “El camino del electrón viene a existir sólo cuando lo observamos”.

La gente sabe desde hace tiempo que cualquier medida perturba la cosa que se está midiendo. Una suposición crucial de las ciencias clásicas ha sido que al menos en principio la perturbación puede hacerse tan pequeña que podemos ignorarla. Así, cuando una antropóloga está estudiando una cultura primitiva en el campo, asume que su presencia en la tribu está teniendo un efecto despreciable en el comportamiento de los miembros. En ocasiones más tarde descubrimos que todo lo que estaba midiendo era el comportamiento de la tribu cuando estaba siendo observado por el antropólogo.

Sin embargo, clásicamente asumimos un modelo donde nosotros, como observadores, estamos detrás de un panel de vidrio donde vemos lo que está pasando “allá afuera”. Ahora sugerimos que el panel de vidrio se ha hecho añicos. Wheeler sugiere que debemos dejar caer la palabra observador por completo, y reemplazarla por participante.

Wheeler ha pensado más profundamente en las consecuencias de un universo participativo que nadie. Él ideó la figura a la derecha, cuyo pie de foto es:

“Representación simbólica del Universo como un sistema autoexcitado traído a la existencia por 'autorreferencia'. El universo da a luz a los participantes comunicantes. Los participantes comunicantes dan sentido al universo... Con tal concepto va la interminable serie de reflejos retrocesivos que uno ve en un par de espejos enfrentados”.

Referencia: J.A. Wheeler en Isham et al., eds, Quantum Gravity (Clarendon, Oxford, 1975), págs. 564-565. Los colores fueron utilizados por Wheeler en un coloquio en el Dept. of Physics, Univ. de Toronto hace algunos años.

Es posible que hayas notado una similitud entre esta visión de la Mecánica Cuántica y la filosofía idealista del obispo Berkeley. Berkeley probablemente habría estado muy contento con el Teorema de Bell. El doctor Johnson estaba, por supuesto, opuesto a Berkeley y solía argumentar en contra de su filosofía gritando “¡Lo refuto así!” mientras pateaba una gran roca. Al parecer, Johnson encontró suficiente consuelo por su argumento de que no le importaba lastimarse el pie.

D'Espagnat también tiende a creer que la suposición de la realidad es incorrecta. Así escribió: “La doctrina de que el mundo está formado por objetos cuya existencia es independiente de la conciencia humana resulta estar en conflicto con la mecánica cuántica y con los hechos establecidos por el experimento”.

En un universo participativo, puedo argumentar que debes tu existencia objetiva a mi amable intervención al permitirte entrar en mi propia conciencia. Así, hay un solipsismo inherente en esta posición. Wigner fue uno de los muchos que estaba muy perturbado por esto.

NO LOCALIDAD Y DAVID BOHM

Recordemos que David Bohm partió a principios de la década de 1950 en una búsqueda de las variables ocultas. Nadie ha explorado las consecuencias de que tales variables sean no locales más profundamente que Bohm, y en la primera subsección a continuación discutiremos algunos de sus trabajos sobre este tema. En la siguiente subsección discutiremos su pensamiento posterior sobre la naturaleza del mundo.

La Orden Implicada

Una buena referencia para el material de esta subsección es David Bohm, La Integridad y el Orden Implicado. Aunque muy profundo el libro no es técnico a excepción del Capítulo 4, que creo que no debería haber sido incluido.

Bohm llamó a nuestro mundo cotidiano del espacio, el tiempo y la causalidad el orden explicativo. Propuso que subyace a este mundo cotidiano uno interconectado al que llama el orden implicado. Utilizó una serie de analogías e imágenes para discutir estos dos órdenes.

En una analogía imaginó un gran recipiente cilíndrico de vidrio de glicerina montado sobre una plataforma giratoria. Colocamos una mancha de tinta negra en la glicerina. Giramos lentamente el recipiente, y la tinta se dispersa gradualmente por toda la glicerina. Si giramos lentamente el cilindro en sentido contrario el punto de tinta se vuelve a formar gradualmente. Cuando la tinta se dispersa se encuentra en un estado implicado: existe a lo largo de la glicerina. Cuando la tinta es una mancha se explica: existe en una parte de la glicerina pero no en las otras partes. Si continuamos rotando el cilindro en esta dirección opuesta el punto se dispersa nuevamente.

Extendemos la imagen de la siguiente manera. Colocamos la mancha de tinta como antes. Lentamente giramos el cilindro una revolución, y la tinta ha comenzado a dispersarse. Colocamos una segunda mancha de tinta justo al lado de donde estaba la primera mancha, y giramos para una revolución más. Se coloca un tercer lugar al lado de donde estaba el segundo, una revolución más, y seguimos con esto por algunos spots. Después continuamos rotando lentamente el cilindro hasta que toda la tinta esté completamente dispersa. Cuando invertimos el sentido de rotación vemos que el último punto se fusiona, luego el siguiente al último justo al lado del último, y así sucesivamente. Podríamos interpretar lo que estamos viendo como una sola mancha de tinta que se mueve. Entonces, en el estado implicado completamente disperso hemos encerrado el movimiento en el espacio y el tiempo de un objeto a lo largo de la glicerina. Invertir la rotación despliega la realidad de nuevo en el espacio y el tiempo.

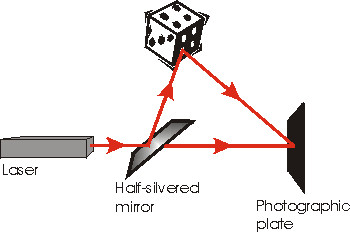Otra analogía es un holograma. Como se muestra a la derecha, para hacer un holograma dividimos un rayo láser en dos piezas con un espejo medio plateado. Una pieza va directamente a una placa fotográfica, la otra rebota en el objeto y luego va a la placa. Para reconstruir la imagen del objeto brillamos un rayo láser a través de la placa desarrollada: aparece la imagen tridimensional. Tenga en cuenta que en algún sentido el holograma en la placa es un patrón de interferencia entre el haz que ha experimentado la cosa y el haz que no experimentó nada.

Una característica de un holograma es que hasta por lo menos unos pocos granos de la plata en la placa, cada pieza de la placa contiene toda la imagen. Si cortamos la placa por la mitad no perdemos la mitad de la imagen; en cambio perdemos resolución y la imagen se vuelve más borrosa. Así, cada pieza de la placa contiene todo el espacio del objeto de manera enplegada; esto es una analogía con el orden implicado. Cuando reconstruimos la imagen, hemos desplegado el orden implicado en uno de explicación.

Hay hologramas “multiplexados” que contienen información de tiempo también. Si el objeto se está moviendo, giramos la placa fotográfica. Cuando reconstruimos la imagen si miramos desde diferentes ángulos vemos el movimiento del objeto. Aquí el comportamiento del tiempo del objeto también se enrosca en la totalidad.

Vemos que en el orden implicado no hay separación espacial ni temporal. Por lo tanto, es un orden no local.

Aquí hay otra imagen utilizada por Bohm:

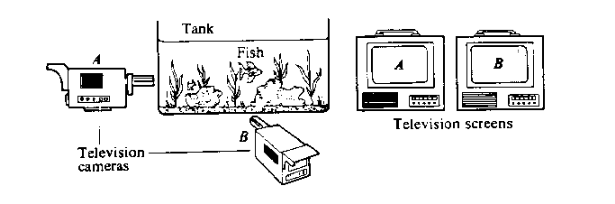
Comenta: “Las imágenes en las pantallas son proyecciones bidimensionales (o facetas) de una realidad tridimensional.... Sin embargo, dado que estas proyecciones solo existen como abstracciones, la realidad tridimensional no es ninguna de estas.... Lo que realmente se encuentra [en las pruebas experimentales del teorema de Bell] es que el comportamiento de los dos [electrones] está correlacionado de una manera bastante similar a la de las dos imágenes televisivas del pez, como se describió anteriormente. Así... cada electrón actúa como si se tratara de una proyección de una realidad de dimensiones superiores.... Lo que aquí estamos proponiendo es que la propiedad cuántica de una relación no local, no causal de elementos distantes pueda entenderse a través de una extensión de la noción descrita anteriormente.” — págs. 187-188.

En la siguiente tabla se compara el orden de explicar e implicar:

Explicar	Implicar
las piezas componen el conjunto	todo compone las partes
separación espacial	holográfica
descriptible	“dedo señalando a la luna”
las cosas existen	'cosa' y 'nada' interfieren
“diez mil cosas”	ilusión
espacio-tiempo	espectros

Dada la integridad ininterrumpida del orden implicado, Bohm preguntó por qué nuestro pensamiento está tan dominado por la fragmentación.

“... la fragmentación se produce continuamente por el hábito casi universal de tomar el contenido de nuestro pensamiento para `una descripción del mundo tal como es'.” — pág. 3.

También escribió sobre qué hacer al respecto:

“[La meditación] es particularmente importante porque... la ilusión de que el yo y el mundo se rompen en fragmentos se origina en el tipo de pensamiento que va más allá de su propia medida y confunde su propio producto con la misma realidad independiente. Para acabar con esta ilusión se requiere de una visión, no sólo del mundo en su conjunto, sino también de cómo está funcionando el instrumento del pensamiento”. — pág. 25.

Ontología de Bohm de la Mecánica Cuántica

En filosofía, la epistemología es el estudio de lo que sabemos y cómo lo conocemos; esto es a diferencia de la ontología que estudia lo que realmente existe. La mayoría de las interpretaciones de la Mecánica Cuántica han sido desarrolladas por personas que simpatizan con la idea de un universo participativo; discutimos esta idea anteriormente. Por lo tanto, estas interpretaciones son esencialmente epistemología.

Para Bohm, esto no fue lo suficientemente bueno. Desarrolló una ontología en sus últimos años. Su obra maestra, El universo indiviso, fue escrita con su colaborador B.J. Hiley y publicada en 1993. Está escrito para físicos, y realmente no puedo recomendarlo a un público no técnico. Aquí exploraremos brevemente algunas de las conclusiones de este libro.

Esencialmente, Bohm y su escuela reinterpretaron las matemáticas de la Mecánica Cuántica y extrajeron una parte de la ecuación que llamaron el potencial cuántico. El potencial cuántico es no local, y es responsable de todos los efectos no locales predichos por la teoría.

El potencial cuántico guía, digamos, la trayectoria de un electrón de una manera similar a la forma en que una radiobaliza puede guiar a un avión que entra para un aterrizaje en el aeropuerto. Son los chorros, alerones, timón, etc. en el avión los que determinan mecánicamente hacia dónde va el avión, pero la baliza guía el camino.

En la ontología de Bohm los electrones son realmente partículas. Para el caso de, por ejemplo, el experimento de doble rendija para electrones, cada electrón pasa por la hendidura superior o la hendidura inferior; tiene una trayectoria definida independiente de su observación. Sin embargo, el potencial cuántico es diferente dependiendo de si la otra hendidura está abierta o cerrada; dado que este potencial no es local puede cambiar instantáneamente si la otra hendidura se abre o cierra. Así, las trayectorias de los electrones son diferentes dependiendo de si la otra hendidura está abierta o no.

Quizás recuerdes que para un sistema caótico, cambios muy pequeños en las condiciones iniciales conducen a trayectorias radicalmente diferentes; puedes leer más sobre esto aquí. Resulta que para el experimento de doble rendija para electrones, el movimiento del electrón después de que haya pasado por las rendijas es caótico precisamente en este sentido. Así, incluso pequeñas fluctuaciones térmicas en la interacción del electrón con las rendijas hacen que el movimiento futuro del electrón sea incognoscible para nosotros, aunque sea estrictamente determinista. Así nos parece que el camino del electrón es aleatorio, aunque en realidad no lo es.

Llamamos clásica a la Física antes que a la Mecánica Cuántica; así las teorías de la relatividad son clásicas Por lo general, caracterizamos una teoría clásica como aquella que incluye observadores y determinismo estricto, mientras que una teoría no clásica tiene participadores y aleatoriedad. Si la interpretación de Bohm es correcta, necesitamos cambiar la forma en que caracterizamos la distinción. Una teoría clásica es local, mientras que una no clásica es no local; ambas son estrictamente deterministas y tienen observadores. Bohm tenía alguna esperanza de que su ontología tuviera consecuencias experimentalmente comprobables, aunque aún no se han realizado tales experimentos.

Quizás desee saber que en el análisis de Bohm el llamado fotón no es una partícula; es un campo electromagnético cuyo comportamiento similar a partículas surge por su interacción con el potencial cuántico.

Obsérvese que en este trabajo, entonces, Bohm finalmente ha identificado la variable oculta que buscó durante tantos años: es el potencial cuántico.

La no localidad de este potencial llevó a Bohm a invocar una imagen muy similar a la que Wheeler utilizó anteriormente en su discusión del universo como sistema autoexcitado:

“La física clásica proporcionaba un espejo que reflejaba únicamente la estructura objetiva del ser humano que era el observador. No hay cabida en este esquema para su proceso mental que es así considerado como separado o como un mero 'epifenómeno' de los procesos objetivos.... [A través del] espejo [de la física cuántica] el observador se ve 'a sí mismo' tanto física como mentalmente en el escenario más amplio del universo en su conjunto.... De manera más amplia se podría decir que a través del ser humano, el universo está haciendo un espejo para observarse a sí mismo”. — Bohm e Hiley, El universo indiviso, pág. 389

Un colega me remarcó que los heroicos intentos de Bohm por mantener una realidad separada de su observación, en esta forma “definitiva”, es peor que la alternativa de no tener una realidad. No sé de la palabra peor, pero después del teorema de Bell algo tiene que dar, ya sea realidad, localidad y/o lógica misma.

Todavía quedan algunas cuestiones sin resolver con respecto a la ontología de Bohm. Por ejemplo, como se discutió en otra parte, el modelo planetario estándar del átomo donde los electrones orbitan el núcleo así como los planetas orbitan el Sol es imposible, ya que según el electromagnetismo clásico tal electrón se encuentra en un estado de movimiento acelerado no uniforme y debe irradiarse su energía, haciendo que se deslice en espiral hacia el núcleo. Sin embargo, cuando pensamos en el electrón en su aspecto de onda, entonces cuando las ondas están en un patrón de onda estacionaria, esto corresponde a las órbitas permitidas del modelo Bohr y los electrones no irradian.

Cuando la idea de tratar al electrón como una onda es desarrollada completamente por la Mecánica Cuántica, las órbitas son más complicadas de lo que se indica en el documento al que se hace referencia en el párrafo anterior.

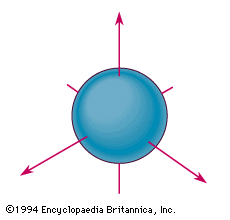A la derecha mostramos la “función de onda” para el electrón en su estado fundamental orbital. Se puede observar que es esféricamente simétrico. En una discusión anterior llamamos a esto la órbita para la cual el número cuántico n es igual a 1.

En la ontología de Bohm, el electrón es una partícula. Pero para esta órbita el electrón es estacionario, con la fuerza eléctrica que intenta introducirlo en el protón siendo simplemente equilibrada por el potencial cuántico. Por lo tanto, este electrón ciertamente no irradiará energía.

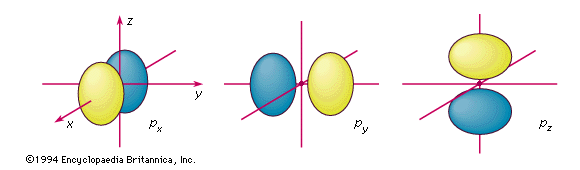
Para el estado con el principio cuántico número 2, existe una función de onda esféricamente simétrica que se parece a la que se muestra antes para n = 1. Pero también hay otros tres orbitales, que se ven como se muestra arriba.

Para los dos primeros de estos orbitales “p”, los electrones se están moviendo y acelerando y se esperaría que irradiaran energía lejos. El último orbital p _z resulta representar un electrón que es estacionario.

Esto está claramente en conflicto con el hecho de que los electrones en el átomo no irradian energía excepto cuando cambian de una órbita permitida a otra órbita permitida.

De hecho, esta dificultad se manifiesta de otra forma en el experimento de doble rendija para electrones. Si el electrón es una partícula que cambia su trayectoria cuando pasa por las rendijas, también debe irradiar energía. Uno de los compañeros de Bohm, Vigier, dijo recientemente que la longitud de onda de esta radiación es muy grande y por lo tanto la pérdida de energía es insignificante; algunas personas creen que Vigier está equivocado. Actualmente se está trabajando en este problema; una de las personas que trabajan en ella es el profesor John Sipe de este Departamento. Me di cuenta de esta polémica al intentar encontrar la respuesta a una pregunta hecha por la ex alumna de la JPU200Y Sharmilla Reid.

---

AUTÓMATAS CELULARES

Un autómata celular proporciona otra aproximación al estudio de la emergencia de estructuras basadas en reglas.

Uno de los autómatas más conocidos es el Juego de la Vida, ideado por John Conway en 1970. Este ejemplo se juega en una gran cuadrícula similar a un tablero de ajedrez. Se inicia con una configuración de celdas en el tablero que están pobladas, y luego se calcula la población en las generaciones siguientes usando tres reglas simples:

1. Nacimiento: una celda desocupada con exactamente 3 vecinos ocupados se poblará en la próxima generación.
2. Supervivencia: una celda ocupada con 2 o 3 vecinos ocupados se poblará en la próxima generación.
3. Muerte: en todos los demás casos una célula está desocupada en la próxima generación.

A pesar de la simplicidad de las reglas, en este juego surgen patrones de movimiento verdaderamente asombrosos, complejidad autoorganizativa y más.

A la derecha se encuentra una animación Flash de la configuración más simple posible que cambia de generación en generación pero que nunca crece ni se apaga.

• Haga clic en el botón Paso para pasar de generación en generación. En este modo se muestra el número de vecinos ocupados de cada celda.
• Haga clic en Reproducir para reanudar la reproducción de la animación.

Hay muchos recursos disponibles en la web para explorar este fascinante “juego” con más detalle.

Si estás leyendo la versión pdf de este documento, las animaciones Flash no están disponibles en pdf.

Se ha propuesto que este tipo de autómatas pueden formar un modelo útil de cómo funciona realmente el universo. Entre los colaboradores de esta idea se encuentran Konrad Zuse en 1967, Edward Fredkin a principios de la década de 1980 y más recientemente Stephen Wolfram en 2002. El trabajo de Wolfram en particular es el resultado de casi una década de trabajo, que se describe en un gigantesco libro autoeditado de 1200 páginas titulado modestamente Un nuevo tipo de ciencia.

Hay dos características clave de los autómatas celulares que son relevantes para esta discusión:

1. Las reglas son siempre estrictamente deterministas.
2. La evolución de una célula depende únicamente de sus vecinos más cercanos.

Esto parece poner un modelo autómata celular de Física en conflicto con el Teorema de Bell, que afirma que un modelo determinístico local lógico del universo no puede ser correcto.

Los defensores del modelo de autómata celular intentan argumentar que no hay conflicto esencial, solo uno aparente. Los argumentos incluyen:

• Que la aparente aleatoriedad de los fenómenos cuánticos es sólo pseudo-aleatoria. A mi me parece que están reintroduciendo la idea de variables ocultas a través de la puerta trasera. Plamen Petrov en uno de los proponentes de este argumento.
• Que hay algún tipo de hilo de mayor dimensión fuera de las cuatro dimensiones normales del espacio y el tiempo. Este “hilo” de alguna manera permitirá conexiones súper luminales. Wolfram y otros han propuesto esta idea.
• Otros partidarios de Wolfram han argumentado que la velocidad de la luz es o puede ser mucho mayor que el valor “habitual” al que estamos acostumbrados. No está claro si necesita ser infinito o no.

En la subsección anterior de Ontología de la Mecánica Cuántica de Bohm, vimos que el intento de Bohm de mantener la causalidad terminó con un mecanismo totalmente no local encapsulado en un Potencial Cuántico. Incluso ahí, vimos al final que hay serios problemas con el modelo.

Puede ser que haya problemas aún más serios con el modelo de Autómata Celular por la forma en que funciona el universo. La polémica sigue siendo muy activa a partir de este escrito (Primavera, 2003). Una lista semialeatoria de lecturas adicionales es:

• arxiv.org/ps_cache/quant-ph/pdf/0206/0206089.pdf
• http://www.math.usf.edu/~eclark/ANKOS_reviews.html
• http://digitalphysics.org/Publications/Petrov/Pet02m/Pet02m.htm

FINALMENTE...

Einstein murió hace muchos años, y así no está aquí para defenderse de reclamos de lo que haría o no haría hoy. No obstante, tiendo a pensar que si hoy estuviera vivo, el teorema de Bell lo obligaría a aceptar la Mecánica Cuántica.