7.2: Girar

Para el momento angular orbital encontramos que\(2 l+1\) debe ser un entero, y además las propiedades espaciales de la función de onda fuerzan\(l\) a ser un entero también. Sin embargo, también podemos construir estados con medio entero\(l\), pero esto debe ser entonces un grado interno de libertad. Esto se llama momento angular de giro, o giro para abreviar. Mostraremos más adelante en el curso que el giro observable se interpreta como un momento magnético intrínseco de un sistema.

Para describir el giro, cambiamos de L a S, que ya no está relacionado con r y p. Las relaciones de conmutación entre los componentes\(S_{i}\) son las mismas que para\(L_{i}\),

\[\left[S_{i}, S_{j}\right]=i \hbar \epsilon_{i j k} S_{k}\tag{7.24}\]

entonces S y L obedecen el mismo álgebra. Las relaciones de conmutación entre S y L, r y p desaparecen:

\[\left[S_{i}, L_{j}\right]=\left[S_{i}, r_{j}\right]=\left[S_{i}, p_{j}\right]=0.\tag{7.25}\]

Por lo tanto, spin genera un espacio vectorial completamente nuevo, ya que conmuta con observables que por sí mismos no conmutan (como\(r_{j}\) y\(p_{j}\)), y es independiente de los grados espaciales de libertad.

Dado que las relaciones de conmutación para S (su álgebra) son las mismas que para L, podemos copiar inmediatamente la estructura algebraica de los autoestados y valores propios:

\ [\ begin {aligned}
&S_ {z}\ izquierda|s, m_ {s}\ derecha\ rangle=m_ {s}\ hbar\ izquierda|s, m_ {s}\ derecha\ rangle,\ quad\ texto {con} s=0,\ frac {1} {2}, 1,\ frac {3} {2}, 2,\ ldots\\
&\ mathbf {S} ^ {2}\ izquierda|s, m_ {s}\ derecha\ rangle=s (s+1)\ hbar^ {2}\ izquierda|s, m_ {s}\ derecha\ rangle.
\ end {alineado}\ tag {7.26}\]

Cuando\(s=\frac{1}{2}\), el sistema tiene dos niveles (un qubit) con spin eigenstates\(\left|\frac{1}{2}, \frac{1}{2}\right\rangle\) y\(\left|\frac{1}{2},-\frac{1}{2}\right\rangle\). A menudo escribimos\(m_{s}=+\frac{1}{2}=\uparrow\) (“arriba”) y\(m_{s}=-\frac{1}{2}=\downarrow\) (“abajo”), que encuentra su origen en los resultados de medición del espín electrónico en un aparato Stern-Gerlach.

Ahora que hemos introducido un espacio vectorial completamente nuevo relacionado con el giro, ¿cómo escribimos la función de onda de una partícula con spin? Sin giro, la función de onda es una función normal de un solo valor\(\psi(\mathbf{r}, t)=\langle\mathbf{r} \mid \psi(t)\rangle\) de coordenadas de espacio y tiempo. Ahora tenemos que sumar el grado de libertad de giro. Para cada giro\(\left(\uparrow \text { or } \downarrow \text { when } s=\frac{1}{2}\right)\), tenemos una función de onda\(\psi_{\uparrow}(\mathbf{r}, t)\) para la partícula con spin up, y\(\psi_{\downarrow}(\mathbf{r}, t)\) para la partícula con spin down. Podemos escribir esto como un vector:

\ [\ psi (\ mathbf {r}, t) =\ left (\ begin {array} {l}
\ psi_ {\ uparrow} (\ mathbf {r}, t)\
\ psi_ {\ flecha abajo} (\ mathbf {r}, t)
\ end {array}\ derecha). \ tag {7.27}\]

El grado de libertad de giro genera un espacio vectorial, después de todo. El vector\(\psi\) se llama espinor.

Los valores de expectativa se evalúan de la manera habitual, pero ahora tenemos que sumar sobre el grado de libertad de giro, así como integrarnos sobre el espacio. Por ejemplo, la probabilidad de encontrar una partícula con giro en una región\(\Omega\) del espacio viene dada por

\[p(\uparrow, \Omega)=\sum_{m_{s}=\uparrow, \downarrow} \int_{\Omega} d \mathbf{r} \delta_{m_{s}, \uparrow}\left|\psi_{m_{s}}(\mathbf{r}, t)\right|^{2}=\int_{\Omega} d \mathbf{r}\left|\psi_{\uparrow}(\mathbf{r}, t)\right|^{2},\tag{7,28}\]

y el valor de expectativa de encontrar una partícula con cualquier giro en una región\(\Omega\) del espacio viene dado por

\[p(\Omega)=\sum_{m_{s}=\uparrow, \downarrow} \int_{\Omega} d \mathbf{r}\left|\psi_{m_{s}}(\mathbf{r}, t)\right|^{2}.\tag{7.29}\]

La normalización de la espinora es tal que

\[\sum_{m_{s}=\uparrow, \downarrow} \int_{V} d \mathbf{r}\left|\psi_{m_{s}}(\mathbf{r}, t)\right|^{2}=1,\tag{7.30}\]

donde\(V\) está todo el espacio disponible para la partícula (esto puede ser todo el universo, o el volumen de una caja con paredes impenetrables, etc.).

Si spin está representado por spinors\((2 s+1)\) -dimensionales (vectores), entonces las transformaciones de espín (operadores) se representan por\((2 s+1) \times(2 s+1)\) matrices. En el caso bidimensional, tenemos por construcción:

\ [S_ {z} |\ uparrow\ rangle=\ frac {\ hbar} {2}\ left (\ begin {array} {l} 1\\ 0
\ end {array}\ derecha)\ quad\ text {y}\ quad S_ {z} |\ flecha abajo\ rangle=-\ frac {\ hbar} {2}\ left (\ begin {array} {l} 0\\ 1\ end {array}\ derecha),\ tag {7.31}\]

lo que significa que la representación matricial de\(S_{z}\) viene dada por

\ [S_ {z} =\ frac {\ hbar} {2}\ left (\ begin {array} {cc}
1 & 0\\
0 & -1
\ end {array}\ right). \ tag {7.32}\]

A continuación, los operadores de escalera actúan de acuerdo con

\[S_{+}|\uparrow\rangle=0, \quad S_{+}|\downarrow\rangle=\hbar|\uparrow\rangle, \quad S_{-}|\uparrow\rangle=\hbar|\downarrow\rangle, \quad S_{-}|\downarrow\rangle=0,\tag{7.33}\]

lo que lleva a la representación matricial

\ [S_ {+} =\ hbar\ izquierda (\ begin {array} {ll} 0 & 1\\ 0 & 0
\ end {array}\ derecha)\ quad\ text {y}\ quad S_ {-} =\ hbar\ izquierda (\ begin {array} {ll} 0 & 0\\ 1 & 0\ end {array}\ derecha). \ tag {7.34}\]

A partir de entonces\(S_{\pm}=S_{x} \pm i S_{y}\) podemos deducir que

\ [S_ {x} =\ frac {\ hbar} {2}\ izquierda (\ begin {array} {ll} 0 & 1\\ 1 & 0
\ end {array}\ derecha)\ quad\ text {y}\ quad S_ {y} =\ frac {\ hbar} {2}\ left (\ begin {array} {cc} 0 & -i\\ i & 0\ end array}\ derecho). \ tag {7.35}\]

A menudo definimos\(S_{i} \equiv \frac{1}{2} \hbar \sigma_{i}\), dónde\(\sigma_{i}\) están las llamadas matrices Pauli. Anteriormente, hemos llamado a estas matrices\(X\),\(Y\), y\(Z\). Las relaciones de conmutación de las matrices Pauli son

\[\left[\sigma_{i}, \sigma_{j}\right]=2 i \epsilon_{i j k} \sigma_{k} \quad \text { or } \quad\left[\frac{\sigma_{i}}{2}, \frac{\sigma_{j}}{2}\right]=i \epsilon_{i j k} \frac{\sigma_{k}}{2}.\tag{7.36}\]

Otras propiedades importantes de las matrices Pauli son

\[\left\{\sigma_{i}, \sigma_{j}\right\} \equiv \sigma_{i} \sigma_{j}+\sigma_{j} \sigma_{i}=2 \delta_{i j} \mathbb{I} \quad \text { (anti-commutator). }\tag{7.37}\]

Ambos son hermitianos y unitarios, y el cuadrado de las matrices Pauli es la identidad:\(\sigma_{i}^{2}=\mathbb{I}\). Además, obedecen una relación de “ortogonalidad”

\[\frac{1}{2} \operatorname{Tr}\left(\sigma_{i} \sigma_{j}\right)=\delta_{i j}.\tag{7.38}\]

El comprobante de esta declaración es el siguiente:

\[\sigma_{i} \sigma_{j}=\sigma_{i} \sigma_{j}+\sigma_{j} \sigma_{i}-\sigma_{j} \sigma_{i}=\left\{\sigma_{i}, \sigma_{j}\right\}-\sigma_{j} \sigma_{i}=2 \delta_{i j}^{\mathbb{I}}-\sigma_{j} \sigma_{i}.\tag{7.39}\]

Tomando el rastro luego rinde

\[\operatorname{Tr}\left(2 \delta_{i j} \mathbb{I}-\sigma_{j} \sigma_{i}\right)=\operatorname{Tr}\left(\sigma_{i} \sigma_{j}\right)=\operatorname{Tr}\left(\sigma_{j} \sigma_{i}\right),\tag{7.40}\]

o (usando\(\operatorname{Tr}(\mathbb{I})=2\))

\[2 \operatorname{Tr}\left(\sigma_{j} \sigma_{i}\right)=4 \delta_{i j},\tag{7.41}\]

lo que prueba la Ec. (7.38). Si definimos\(\sigma_{0} \equiv \mathbb{I}\), podemos extender esta prueba al caso de cuatro dimensiones

\[\frac{1}{2} \operatorname{Tr}\left(\sigma_{\mu} \sigma_{v}\right)=\delta_{\mu v}\tag{7.42}\]

con\(\mu, v=0,1,2,3\).

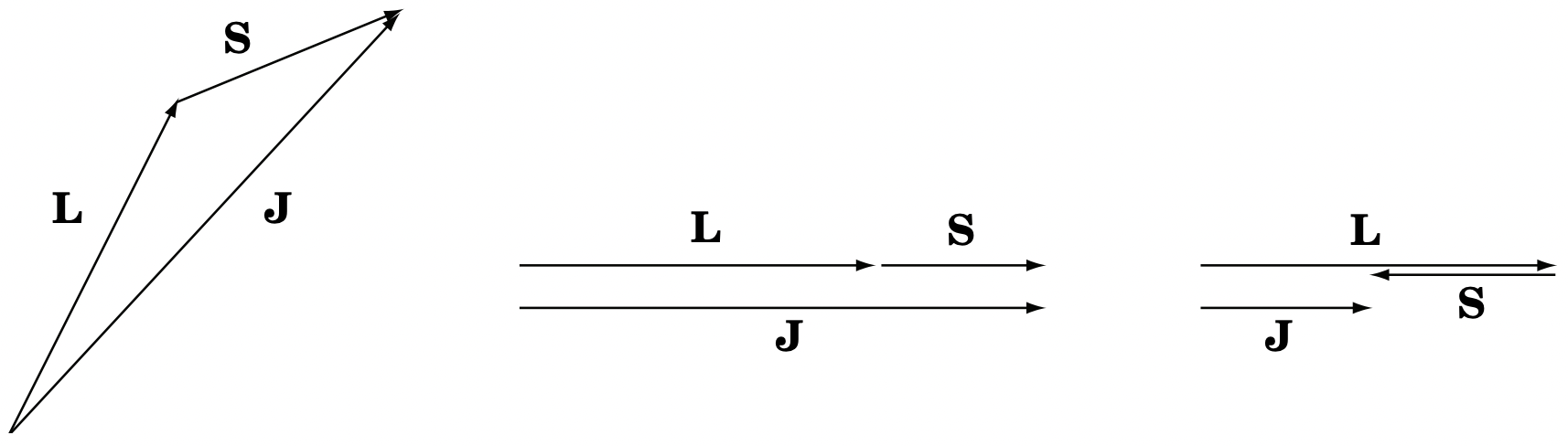Figura 3: Adición de momento angular.

Entonces podemos escribir cualquier matriz 2×2 como una suma sobre los operadores Pauli bidimensionales:

\[A=\sum_{\mu} a_{\mu} \sigma_{\mu},\tag{7.43}\]

desde

\ (\ frac {1} {2}\ nombreoperador {Tr}\ izquierda (A\ sigma_ {v}\ derecha) =\ frac {1} {2}\ nombre_operador {Tr}\ izquierda (\ suma_ {\ mu} a_ {\ mu}\ sigma_ {\ mu}\ sigma_ {v}\ derecha) =\ frac {1} {2} suma_ {\ mu} a_ {\ mu}\ nombreoperador {Tr}\ izquierda (\ sigma_ {\ mu}\ sigma_ {v}\ derecha) =\ suma_ {\ mu} a_ {\ mu}\ delta_ {\ mu v} =a_ {v}\ tag {7.44}\]

Las matrices Pauli y la matriz de identidad forman una base para las matrices 2×2, y podemos escribir

\ [a=a_ {0}\ mathbb {I} +\ mathbf {a}\ cdot\ sigma=\ left (\ begin {array} {cc}
a_ {0} +a_ {z} & a_ {x} -i a_ {y}\\
a_ {x} +i a_ {y} & a_ {0} -a_ {z}
\ end {array}\ derecha)\ tag {7.45}\]

donde usamos la notación\(\boldsymbol{\sigma}=\left(\sigma_{x}, \sigma_{y}, \sigma_{z}\right)\).