6.8: Problemas de ejercicio

6.1. Utilice la Ec. (14) para probar la siguiente forma general del teorema de Hellmann-Feynman (cuya prueba en el dominio de la mecánica de onda fue la tarea del Problema 1.5):\[\frac{\partial E_{n}}{\partial \lambda}=\left\langle n\left|\frac{\partial \hat{H}}{\partial \lambda}\right| n\right\rangle,\] donde\(\lambda\) es un parámetro arbitrario de\(c\) número.

6.2. Establecer una relación entre la Ec. (16) y el resultado de la teoría clásica de oscilaciones débilmente anarmónicas (“no lineales”) a amortiguamiento insignificante.

Pista: Es posible que te guste usar el razonamiento de N. Bohr discutido en Problema 1.1.

6.3. Se ejerce una fuerza\(F\) débil e independiente del tiempo sobre una partícula 1D que se colocó en un pozo de potencial de pared dura.\[U(x)= \begin{cases}0, & \text { for } 0<x<a \\ +\infty, & \text { otherwise }\end{cases}\] Calcular, bosquejar y discutir la perturbación de\(1^{\text {st }}\) orden de su función de onda en estado fundamental.

6.4. Una fuerza independiente del tiempo\(\mathbf{F}=\mu\left(\mathbf{n}_{x} y+\mathbf{n}_{y} x\right)\), donde\(\mu\) es una pequeña constante, se aplica a un oscilador\(3 \mathrm{D}\) armónico de masa\(m\) y frecuencia\(\omega_{0}\), ubicado en el origen. Calcular, en el primer orden de la teoría de la perturbación, el efecto de la fuerza sobre la energía del estado fundamental del oscilador, y su nivel de energía excitada más bajo. ¿Qué tan pequeña debe\(\mu\) ser la constante para que tus resultados sean cuantitativamente correctos?

6.5. Una partícula 1D de masa\(m\) se localiza en un pozo de potencial estrecho que puede aproximarse con una función delta:\[U(x)=-w \delta(x), \quad \text { with } w>0 .\] Calcular el cambio de su energía de estado fundamental por una fuerza adicional débil e independiente del tiempo\(F\), en la primera aproximación no desaparecida del teoría de la perturbación. Discutir los límites de validez de este resultado, tomando en cuenta que en\(F \neq 0\), el estado localizado de la partícula es metaestable.

6.6. Utilizar la teoría de la perturbación para calcular los valores propios del operador\(\hat{L}^{2}\) en el límite\(|m| \approx l\)\(>>1\), por medios puramente onda-mecánicos.

Pista: Pruebe la siguiente sustitución:\(\Theta(\theta)=f(\theta) / \sin ^{1 / 2} \theta\).

6.7. En el orden de no fuga más bajo de la teoría de perturbación, calcule el desplazamiento de la energía del estado fundamental de un rotador esférico cargado eléctricamente (es decir\(m\), una partícula de masa, libre para moverse sobre una superficie esférica de radio\(R\)) debido a una débil, uniforme, campo eléctrico independiente\(\mathscr{E}\). 6.8. Utilice la teoría de perturbación para evaluar el efecto de un campo eléctrico uniforme e independiente del tiempo\(\mathscr{E}\) sobre la energía del estado fundamental\(E_{\mathrm{g}}\) de un átomo de hidrógeno. En particular:

(i) calcular el cambio\(2^{\text {nd }}\) -orden de\(E_{\mathrm{g}}\), descuidar los estados extendidos no perturbados con\(E>0\), y llevar el resultado a la forma analítica más simple que pueda,

(ii) encontrar los límites inferior y superior en el turno, y

(iii) discutir las manifestaciones experimentales más simples de este efecto cuadrático Stark.

6.9. Una partícula de masa\(m\), con carga eléctrica\(q\), se encuentra en su\(s\) estado fundamental con una energía dada\(E_{\mathrm{g}}<\) 0, siendo localizada por un pozo de potencial esféricamente simétrico de muy corto alcance. Calcular su polarizabilidad eléctrica estática\(\alpha\).

6.10. En algunos átomos, el efecto de cribado de carga de otros electrones sobre el movimiento de cada uno de ellos puede aproximarse razonablemente bien mediante la sustitución del potencial de Coulomb\((3.190), U=-C / r\), con el llamado potencial de Hulthén\[U=-\frac{C / a}{\exp \{r / a\}-1} \rightarrow-C \times \begin{cases}1 / r, & \text { for } r<<a, \\ \exp \{-r / a\} / a, & \text { for } a<<r .\end{cases}\] Suponiendo que el radio de cribado efectivo\(a\) es mucho mayor que\(r_{0} \equiv \hbar^{2} / m C\), utilizar la teoría de la perturbación para calcular el espectro energético de una sola partícula de masa\(m\), moviéndose en este potencial, en el orden más bajo necesario para levantar la\(l\) degeneración de los niveles.

6.11. En el orden de no fuga más bajo de la teoría de perturbación, calcule la corrección a las energías del estado fundamental y todos los estados más bajos excitados de un átomo/ion similar al hidrógeno, debido a la penetración del electrón en su núcleo, modelando como una esfera de radio sin espinas, uniformemente cargada\(R<<r_{\mathrm{B}} / Z\).

6.12. Demostrar que el operador de corrección cinético-relativista (48) de hecho solo tiene elementos de matriz diagonal en base a estados atómicos de Bohr no perturbados (3.200).

6.13. Calcular la corrección relativista de orden más bajo a la energía del estado fundamental de un oscilador\(1 \mathrm{D}\) armónico.

6.14. Utilizar la teoría de la perturbación para calcular la contribución a la susceptibilidad magnética\(\chi_{\mathrm{m}}\) de un gas diluido, esto es debido al movimiento orbital de un solo electrón dentro de cada partícula de gas. Deletrea tu resultado para un estado fundamental esféricamente simétrico del electrón, y da am estimación de la magnitud de esta susceptibilidad orbital.

6.15. ¿Cómo calcular el levantamiento de degeneración del nivel de energía, por una perturbación independiente del tiempo, en el\(2^{\text {nd }}\) orden de la perturbación en\(\hat{H}^{(1)}\), suponiendo que no se levanta en el\(1^{\text {st }}\) orden? Realizar dicho cálculo para un rotador plano de masa\(m\) y radio\(R\), llevando carga eléctrica\(q\), y colocado en un campo eléctrico débil, uniforme y constante\(\mathscr{E}\).

6.16. \({ }^{*}\)El hamiltoniano de un sistema cuántico cambia lentamente en el tiempo.

(i) Desarrollar una teoría de las transiciones cuánticas en el sistema, y deletrear su resultado en el\(1^{\text {st }}\) orden en la velocidad del cambio. (ii) Utilizar el resultado\(1^{\text {st }}\) -order para calcular la probabilidad de que un pulso de tiempo finito de una fuerza que cambia lentamente\(F(t)\) conduzca un oscilador armónico 1D, inicialmente en su estado fundamental, a un estado excitado.

(iii) Comparar el último resultado con el exacto.

6.17. Utilizar el modelo de partícula única para calcular la permitividad eléctrica compleja\(\varepsilon(\omega)\) de un gas diluido de átomos similares, debido a su polarización eléctrica inducida por un campo ac externo débil, para una frecuencia de campo\(\omega\) muy cercana a una de las frecuencias de transición cuántica \(\omega_{n n}\). Con base en el resultado, calcular y estimar la sección transversal de absorción de cada átomo.

Sugerencia: En el modelo de una sola partícula, las propiedades de los átomos están determinadas por electrones\(Z\) similares que no interactúan, cada uno moviéndose en un potencial de atracción estática similar, generalmente diferente del Coulomb, porque es aportado no solo por el núcleo, sino también por otros electrones.

6.18. Utilizar la solución del problema anterior para generalizar la expresión de la fuerza de dispersión de Londres entre dos átomos (cuyo cálculo en el modelo armónico-oscilador fue objeto de Problemas\(3.16\) y 5.15) al modelo de partícula única con un espectro de energía arbitrario.

6.19. Utilizar la solución del problema anterior para calcular la energía potencial de interacción de dos átomos de hidrógeno, ambos en su estado fundamental, separados por la distancia\(r \gg r_{\mathrm{B}}\).

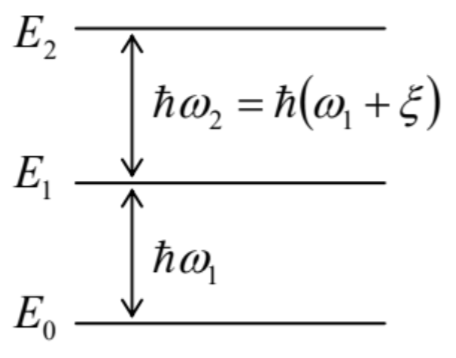
6.20. En cierto sistema cuántico, las distancias entre los tres niveles de energía más bajos son ligeramente diferentes\(-\) ver la figura a la derecha\(\left(|\xi|<<\omega_{1,2}\right)\). Suponiendo que los elementos de la matriz involucrados de la perturbación hamiltoniana son conocidos, y todos son proporcionales a la amplitud del campo ac externo, encontrar el tiempo necesario para poblar el primer nivel excitado casi por completo (con una precisión dada\(\varepsilon<<1\)), utilizando el efecto de oscilación de Rabi, si en\(t=0\) el sistema está completamente en su estado fundamental.

6.21. \({ }^{*}\)Analizar la posibilidad de una transferencia lenta de un sistema de uno de sus niveles de energía a otro (en la figura de la derecha, del nivel 1 al nivel\(3)\), utilizando el esquema mostrado en esa figura, en el que las amplitudes de excitación externa monocromática \(A_{+}\)y\(A_{-}\) puede cambiarse lentamente a voluntad.

6.22. Un pulso de fuerza externa débil\(F(t)\), de duración finita, se aplica a un oscilador armónico 1D que inicialmente estaba en su estado fundamental.

(i) Calcular, en el orden de no fuga más bajo de la teoría de perturbación, la probabilidad de que el pulso conduzca al oscilador a su estado de excitación más bajo.

(ii) Comparar el resultado con la solución exacta del problema.

iii) Deletrear el resultado perturbador de una forma de onda gaussiana\[F(t)=F_{0} \exp \left\{-t^{2} / \tau^{2}\right\},\] y analizar su dependencia de la escala\(\tau\) de la duración del pulso.

6.23. Un campo eléctrico externo espacialmente uniforme, pero dependiente del tiempo,\(\mathscr{E}(t)\) se aplica, a partir de\(t=0\), a un rotador plano cargado, inicialmente en su estado fundamental. (i) Calcular, en el orden de no fuga más bajo en la fuerza del campo, la probabilidad de que por el tiempo\(t>0\), el rotador se encuentre en su estado\(n^{\text {th }}\) excitado.

(ii) Deletrea y analiza tus resultados para un campo de magnitud constante que gira, con una velocidad angular constante\(\omega\), dentro del plano del rotador.

(iii) Hacer lo mismo para un campo monocromático de frecuencia\(\omega\), con una polarización fija.

6.24. Un giro-\(1 / 2\) con una relación giromagnética\(\gamma\) se coloca en un campo magnético que incluye un componente independiente del tiempo\(\mathscr{B}_{0}\), y un campo perpendicular de magnitud constante\(\mathscr{B}_{\mathrm{r}}\), girado con una velocidad angular constante \(\omega\). ¿Se puede reducir este problema de resonancia magnética a uno ya discutido en el Capítulo 6?

6.25. Desarrollar la teoría general de las excitaciones cuánticas de los niveles superiores de un sistema de espectro discreto, inicialmente en el estado fundamental, por una perturbación débil dependiente del tiempo, hasta el\(2^{\text {nd }}\) orden. Deletrear y discutir el resultado para el caso de excitación monocromática, con una afinación casi perfecta de su frecuencia\(\omega\) a la mitad de una cierta frecuencia de transición cuántica\(\omega_{n 0} \equiv\left(E_{n}-E_{0}\right) / \hbar\).

6.26. Una partícula pesada, relativista, con carga eléctrica\(q=Z e\), pasa por un átomo de hidrógeno, inicialmente en su estado fundamental, con un parámetro de impacto\(b\) dentro del rango\(r_{\mathrm{B}}<<b<<r_{\mathrm{B}} / \alpha\), donde\(\alpha \approx\)\(1 / 137\) está la constante de estructura fina. Calcular las probabilidades de la transición del átomo a sus estados más bajos excitados.

6.27. Una partícula de masa\(m\) se encuentra inicialmente en estado basal localizado, con energía\(E_{\mathrm{g}}<0\), de un pozo de potencial esféricamente simétrico muy pequeño. Calcular la tasa de su deslocalización mediante una fuerza clásica aplicada\(\mathbf{F}(t)=\mathbf{n} F_{0} \cos \omega t\) con una dirección independiente del tiempo\(\mathbf{n}\).

6.28. \({ }^{*}\)Calcular la tasa de ionización de un átomo de hidrógeno, inicialmente en su estado fundamental, mediante una onda electromagnética clásica polarizada linealmente con amplitud de campo eléctrico\(\mathscr{E}_{0}\), y una frecuencia\(\omega\) dentro del rango\[\hbar / m_{\mathrm{e}} r_{\mathrm{B}}^{2}<<\omega<c / r_{\mathrm{B}},\] donde \(r_{\mathrm{B}}\)es el radio de Bohr. Refunde tu resultado en términos de la sección transversal de la absorción de ondas electromagnéticas. Discutir brevemente qué cambios de la teoría serían necesarios si se hubiera violado alguna de las condiciones anteriores.

6.29. \({ }^{*}\)Utilice la Regla de Oro cuántico-mecánica para derivar la expresión general de la corriente eléctrica\(I\) a través de una débil unión túnel entre dos conductores, polarizados con voltaje de CC\(V\), tratando los conductores como gases Fermi degenerados de electrones con interacción directa despreciable. Simplifique el resultado en el límite de baja tensión.

Sugerencia: La corriente eléctrica que fluye a través de una unión de túnel débil es tan baja que no perturbe sustancialmente los estados electrónicos dentro de cada conductor.

6.30. {} ^ {*}\) Generalizar el resultado del problema anterior al caso cuando una unión de túnel débil está polarizada con voltaje\(V(t)=V_{0}+A \cos \omega t\), con\(\hbar \omega\) generalmente comparable con\(e V_{0}\) y\(e A\).

6.31. {} ^ {*}\) Usa la Regla de Oro cuántico-mecánica para derivar la fórmula Landau-Zener (2.257).