7.2: Representación de coordenadas y la función Wigner
- Page ID
- 130890
Para muchas aplicaciones del operador de densidad, su representación de coordenadas es conveniente. (Solo lo discutiré para el caso 1D; la generalización a casos multidimensionales es sencilla). Siguiendo la Eq. (4.47), es natural definir la siguiente función de dos argumentos (tradicionalmente, también llamada matriz de densidad):
Matriz de densidad: representación de coordenadas
\[\ w\left(x, x^{\prime}\right) \equiv\left\langle x|\hat{w}| x^{\prime}\right\rangle\]
Insertando, en el lado derecho de esta definición, dos condiciones de cierre (4.44) para una base arbitraria (pero completa y ortonormal)\(\{s\}\), y luego usando la Ec. (4.233),\({ }^{13}\) obtenemos\[w\left(x, x^{\prime}\right)=\sum_{j, j^{\prime}}\left\langle x \mid s_{j}\right\rangle\left\langle s_{j}|\hat{w}| s_{j^{\prime}}\right\rangle\left\langle s_{j^{\prime}} \mid x^{\prime}\right\rangle=\left.\sum_{j, j^{\prime}} \psi_{j}(x) w_{j j^{\prime}}\right|_{\text {in } s} \psi_{j^{\prime}}^{*}\left(x^{\prime}\right)\] En la base especial\(\{w\}\), en la que se encuentra la matriz de densidad diagonal, esta expresión se reduce a\[w\left(x, x^{\prime}\right)=\sum_{j} \psi_{j}(x) W_{j} \psi_{j}^{*}\left(x^{\prime}\right) .\] Vamos a discutir las propiedades de esta función. En argumentos coincidentes,\(x^{\prime}=x\), esto es solo la densidad de probabilidad:\({ }^{14}\)\[w(x, x)=\sum_{j} \psi_{j}(x) W_{j} \psi_{j}^{*}(x)=\sum_{j} w_{j}(x) W_{j}=w(x) .\] Sin embargo, la matriz de densidad da más información sobre el sistema que solo la densidad de probabilidad. Como ejemplo más simple, consideremos un estado cuántico puro, con\(W_{j}=\delta_{j, j}\), para que\(\psi(x)=\psi_{j}^{\prime}(x)\), y\[w\left(x, x^{\prime}\right)=\psi_{j^{\prime}}(x) \psi_{j^{\prime}}^{*}\left(x^{\prime}\right) \equiv \psi(x) \psi^{*}\left(x^{\prime}\right) .\] Vemos que la matriz de densidad lleva la información no sólo sobre el módulo sino también sobre la fase de la función de onda. (Por supuesto, se puede argumentar de manera bastante convincente que en este límite último la descripción de la matriz de densidad es redundante porque toda esta información está contenida en la función de onda misma).
¿Cómo se puede interpretar la matriz de densidad? En el caso simple (31), podemos escribir de\[\left|w\left(x, x^{\prime}\right)\right|^{2} \equiv w\left(x, x^{\prime}\right) w^{*}\left(x, x^{\prime}\right)=\psi(x) \psi^{*}(x) \psi\left(x^{\prime}\right) \psi^{*}\left(x^{\prime}\right)=w(x) w\left(x^{\prime}\right),\] manera que el módulo al cuadrado de la matriz de densidad sea igual que la densidad de probabilidad conjunta para encontrar el sistema en el punto\(x\) y el punto\(x\) '. Por ejemplo, para un paquete de onda simple con una extensión espacial\(\delta x\),\(w\left(x, x^{\prime}\right)\) tiene una magnitud apreciable solo si ambos puntos no están más\(\sim \delta x\) lejos que del centro del paquete, y por lo tanto uno del otro. La interpretación se vuelve más compleja si tratamos con una mezcla incoherente de varias funciones de onda, por ejemplo, la mezcla clásica que describe el equilibrio termodinámico. En este caso, podemos usar la ecuación (24) para reescribir la ecuación (29) de la siguiente manera:\[w\left(x, x^{\prime}\right)=\sum_{n} \psi_{n}(x) W_{n} \psi_{n}^{*}\left(x^{\prime}\right)=\frac{1}{Z} \sum_{n} \psi_{n}(x) \exp \left\{-\frac{E_{n}}{k_{\mathrm{B}} T}\right\} \psi_{n}^{*}\left(x^{\prime}\right) .\] Como ejemplo más simple, veamos cuál es la matriz de densidad de una partícula libre (1D) en el equilibrio térmico. Como ya sabemos muy bien, en este caso, el conjunto de energías\(E_{p}=p^{2} / 2 m\) de estados estacionarios (ondas monocromáticas) forma un continuo, por lo que necesitamos reemplazar la suma (33) por una integral, utilizando por ejemplo las funciones propias de onda viajera “delta normalizadas” (4.264):\[w\left(x, x^{\prime}\right)=\frac{1}{2 \pi \hbar Z} \int_{-\infty}^{+\infty} \exp \left\{-\frac{i p x}{\hbar}\right\} \exp \left\{-\frac{p^{2}}{2 m k_{B} T}\right\} \exp \left\{\frac{i p x^{\prime}}{\hbar}\right\} d p .\] Esta es una habitual integral gaussiana, y puede elaborarse, como lo hemos hecho repetidamente en el Capítulo 2 y más allá, complementando el exponente al cuadrado completo del impulso\(p\) más una constante. La suma estadística también se\(Z\) puede calcular fácilmente,\({ }^{15}\)\[Z=\left(2 \pi m k_{B} T\right)^{1 / 2},\] sin embargo, para lo que sigue es más útil escribir el resultado para el producto\(w Z\) (la llamada matriz de densidad\(u n\) normalizada):\[w\left(x, x^{\prime}\right) Z=\left(\frac{m k_{\mathrm{B}} T}{2 \pi \hbar^{2}}\right)^{1 / 2} \exp \left\{-\frac{m k_{\mathrm{B}} T\left(x-x^{\prime}\right)^{2}}{2 \hbar^{2}}\right\} .\] Esta es una resultado muy interesante: la matriz de densidad depende solo de la diferencia de sus argumentos, cayendo a cero rápido ya que la distancia entre los puntos\(x\) y\(x\) 'excede la siguiente escala característica (llamada la longitud de correlación)\[x_{\mathrm{c}} \equiv\left\langle\left(x-x^{\prime}\right)^{2}\right\rangle^{1 / 2}=\frac{\hbar}{\left(m k_{\mathrm{B}} T\right)^{1 / 2}} .\] Esta longitud puede ser interpretados de la siguiente manera. Es sencillo usar la Ec. (24) para verificar que la energía promedio\(\langle E\rangle=\left\langle p^{2} / 2 m\right\rangle\) de una partícula libre en el equilibrio térmico, es decir, en la mezcla clásica (33), es igual\(k_{\mathrm{B}} T / 2\). De ahí que la magnitud promedio del momento de la partícula pueda estimarse de\[p_{\mathrm{c}} \equiv\left\langle p^{2}\right\rangle^{1 / 2}=(2 m\langle E\rangle)^{1 / 2}=\left(m k_{\mathrm{B}} T\right)^{1 / 2},\] manera que\(x_{\mathrm{c}}\) sea del orden de la longitud mínima permitida por la “relación de incertidumbre” similar a Heisenberg:\[x_{\mathrm{c}}=\hbar / p_{\mathrm{c}} .\] Obsérvese que con el crecimiento de la temperatura, la longitud de correlación (37) va a cero, y la matriz de densidad (36) tiende a una función delta:\[\left.w\left(x, x^{\prime}\right) Z\right|_{T \rightarrow \infty} \rightarrow \delta\left(x-x^{\prime}\right) .\] Dado que en este límite la energía cinética promedio de la partícula no es menor que su energía potencial en cualquier perfil de potencial fijo, la Ec. (40) es la propiedad general de la matriz de densidad (33).
Discutamos la siguiente característica curiosa de la ecuación (36): si reemplazamos\(k_{\mathrm{B}} T\) con\(\hbar / i\left(t-t_{0}\right)\), y, con\(x\)\(x_{0}\), la matriz de densidad no normalizada\(w Z\) para una partícula libre se convierte en el propagador de la partícula \(-\mathrm{cf}\). Eq. (2.49). Esto no es sólo una coincidencia ocasional. En efecto, en el capítulo 2 vimos que el propagador de un sistema con un hamiltoniano estacionario arbitrario puede expresarse a través de las funciones propias estacionarias como
\[G\left(x, t ; x_{0}, t_{0}\right)=\sum_{n} \psi_{n}(x) \exp \left\{-i \frac{E_{n}}{\hbar}\left(t-t_{0}\right)\right\} \psi_{n}^{*}\left(x_{0}\right)\]Comparando esta expresión con la Ec. (33), vemos que los reemplazos\[\frac{i\left(t-t_{0}\right)}{\hbar} \rightarrow \frac{1}{k_{\mathrm{B}} T}, \quad x_{0} \rightarrow x^{\prime},\] convierten al propagador de estado puro\(G\) en la matriz\(w Z\) de densidad no normalizada del mismo sistema en equilibrio termodinámico. Este hecho importante, enraizado en la similitud formal de la distribución de Gibbs (24) con la solución de la ecuación de Schrödinger (1.69), permite una técnica teórica de las llamadas funciones del Green termodinámico, que es especialmente productiva en la física de la materia condensada. \({ }^{16}\)
Para nuestros propósitos actuales, podemos emplear la ecuación (42) para reutilizar algunos de los resultados de la mecánica de onda, en particular, la siguiente fórmula para el propagador del oscilador armónico\[G\left(x, t ; x_{0}, t_{0}\right)=\left(\frac{m \omega_{0}}{2 \pi i \hbar \sin \left[\omega_{0}\left(t-t_{0}\right)\right]}\right)^{1 / 2} \exp \left\{-\frac{m \omega_{0}\left[\left(x^{2}+x_{0}^{2}\right) \cos \left[\omega_{0}\left(t-t_{0}\right)\right]-2 x x_{0}\right]}{2 i \hbar \sin \left[\omega_{0}\left(t-t_{0}\right)\right]}\right\} .\] que puede demostrarse fácilmente que satisface la ecuación de Schrödinger para el hamiltoniano (5.62), con la inicial apropiada condición:\(G\left(x, t_{0} ; x_{0}, t_{0}\right)=\delta\left(x-x_{0}\right)\). Haciendo la sustitución (42), inmediatamente obtenemos
Oscilotor armónico en equilibrio térmico
\[\ w\left(x, x^{\prime}\right) Z=\left[\frac{m \omega_{0}}{2 \pi \hbar \sinh \left(\hbar \omega_{0} / k_{\mathrm{B}} T\right)}\right]^{1 / 2} \exp \left\{-\frac{m \omega_{0}\left[\left(x^{2}+x^{\prime 2}\right) \cosh \left(\hbar \omega_{0} / k_{\mathrm{B}} T\right)-2 x x^{\prime}\right]}{2 \hbar \sinh \left(\hbar \omega_{0} / k_{\mathrm{B}} T\right)}\right\} .\]
Como comprobación de cordura, a temperaturas muy bajas\(k_{\mathrm{B}} T<<\hbar \omega_{0}\), ambas funciones hiperbólicas que participan en esta expresión son muy grandes y casi iguales, y rinde\[\left.w\left(x, x^{\prime}\right) Z\right|_{T \rightarrow 0} \rightarrow\left[\left(\frac{m \omega_{0}}{\pi \hbar}\right)^{1 / 4} \exp \left\{-\frac{m \omega_{0} x^{2}}{\hbar}\right\}\right] \times \exp \left\{-\frac{\hbar \omega_{0}}{2 k_{\mathrm{B}} T}\right\} \times\left[\left(\frac{m \omega_{0}}{\pi \hbar}\right)^{1 / 4} \exp \left\{-\frac{m \omega_{0} x^{\prime 2}}{\hbar}\right\}\right] \cdot\] En cada una de las expresiones entre corchetes podemos reconocer fácilmente la función de onda del estado fundamental (2.275) del oscilador, mientras que el exponente medio es solo la suma estadística (24) en el límite de baja temperatura cuando está dominado por la contribución a nivel del suelo:\[\left.Z\right|_{T \rightarrow 0} \rightarrow \exp \left\{-\frac{\hbar \omega_{0}}{2 k_{\mathrm{B}} T}\right\} .\] Como resultado,\(Z\) en ambas partes de la Ec. (45) puede cancelarse, y la matriz de densidad en este límite es descrita por la Ec. (31), con el estado fundamental como el único estado del sistema. Esto es natural cuando la temperatura es demasiado baja para la excitación térmica de cualquier otro estado.
Volviendo a temperaturas arbitrarias, la Ec. (44) en argumentos coincidentes da la siguiente expresión para la densidad de probabilidad:\({ }^{17}\)\[w(x, x) Z \equiv w(x) Z=\left[\frac{m \omega_{0}}{2 \pi \hbar \sinh \left(\hbar \omega_{0} / k_{B} T\right)}\right]^{1 / 2} \exp \left\{-\frac{m \omega_{0} x^{2}}{\hbar} \tanh \frac{\hbar \omega_{0}}{2 k_{\mathrm{B}} T}\right\} .\] Esta es solo una función gaussiana de\(x\), con la siguiente varianza:\[\left\langle x^{2}\right\rangle=\frac{\hbar}{2 m \omega_{0}} \operatorname{coth} \frac{\hbar \omega_{0}}{2 k_{\mathrm{B}} T} .\] Para comparar este resultado con nuestros anteriores, es útil refundirla como\[\langle U\rangle=\frac{m \omega_{0}^{2}}{2}\left\langle x^{2}\right\rangle=\frac{\hbar \omega_{0}}{4} \operatorname{coth} \frac{\hbar \omega_{0}}{2 k_{\mathrm{B}} T} .\] Comparando esta expresión con la Ec. (26), vemos que el valor promedio de la energía potencial es exactamente la mitad de la energía total, siendo la otra mitad la energía cinética promedio. Esto es lo que podríamos esperar, porque según las ecuaciones (5.96) - (5.97), tal relación se mantiene para cada estado Fock y por lo tanto también debería sostenerse para su mezcla clásica.
Desafortunadamente, además del caso trivial (30) de argumentos coincidentes, es difícil dar una interpretación directa de la función de densidad en términos de las mediciones del sistema. Esta es una dificultad fundamental, que ha sido bien explorada en términos de la función Wigner (a veces llamada la “distribución Wigner-Ville”)\({ }^{18}\) definida como\[W(X, P) \equiv \frac{1}{2 \pi \hbar} \int w\left(X+\frac{\widetilde{X}}{2}, X-\frac{\widetilde{X}}{2}\right) \exp \left\{-\frac{i P \widetilde{X}}{\hbar}\right\} d \widetilde{X}\] Desde el punto de vista matemático, esto es solo la transformada de Fourier de la matriz de densidad en una de dos nuevas coordenadas definido por las siguientes relaciones (ver Fig. 2):\[X \equiv \frac{x+x^{\prime}}{2}, \quad \widetilde{X} \equiv x-x^{\prime}, \quad \text { so that } x \equiv X+\frac{\widetilde{X}}{2}, \quad x^{\prime} \equiv X-\frac{\widetilde{X}}{2} .\] Físicamente, el nuevo argumento\(X\) puede interpretarse como la posición promedio de la partícula durante el intervalo de tiempo\(\left(t-t^{\prime}\right)\), mientras que\(\widetilde{X}\), como la distancia que pasó por ella durante ese intervalo de tiempo, así que\(P\) caracteriza el impulso de la partícula durante ese movimiento. Como resultado, la función Wigner es un constructo matemático destinado a caracterizar la distribución de probabilidad del sistema simultáneamente en la coordenada y el espacio de impulso -para sistemas 1D, en el plano de fase\([X, P]\), que habíamos discutido anteriormente- ver Fig. 5.8. Veamos cuán fructífera es esta intención.
En primer lugar, podemos escribir la transformada de Fourier recíproca a la Ec. (50):\[w\left(X+\frac{\tilde{X}}{2}, X-\frac{\tilde{X}}{2}\right)=\int W(X, P) \exp \left\{\frac{i P \widetilde{X}}{\hbar}\right\} d P \text {. }\] Para el caso particular\(\widetilde{X}=0\), esta relación rinde\[w(X) \equiv w(X, X)=\int W(X, P) d P .\] De ahí que la integral de la función Wigner sobre el impulso\(P\) da la densidad de probabilidad para encontrar el sistema en un punto \(X\)- tal como lo hace para una función de distribución clásica\(w_{\mathrm{cl}}(X, P) .{ }^{19}\)
A continuación, la función Wigner tiene la propiedad similar para la integración sobre\(X\). Para probar este hecho, podemos introducir primero la representación de impulso de la matriz de densidad, en total analogía con su representación de coordenadas (27):\[w\left(p, p^{\prime}\right) \equiv\left\langle p|\hat{w}| p^{\prime}\right\rangle .\] Insertando, como de costumbre, dos operadores de identidad, en la forma dada por la Ec. (4.252), en el lado derecho de esta igualdad, obtenemos la siguiente relación entre las representaciones de impulso y coordenadas:\[w\left(p, p^{\prime}\right)=\iint d x d x^{\prime}\langle p \mid x\rangle\left\langle x|\hat{w}| x^{\prime}\right\rangle\left\langle x^{\prime} \mid p^{\prime}\right\rangle=\frac{1}{2 \pi \hbar} \iint d x d x^{\prime} \exp \left\{-\frac{i p x}{\hbar}\right\} w\left(x, x^{\prime}\right) \exp \left\{+\frac{i p^{\prime} x^{\prime}}{\hbar}\right\} .\] Esto no es, por supuesto, otra cosa que la transformación unitaria de un operador de la\(x\) -base a la\(p\) -base, similar a la primera forma de la Ec. (4.272). Para argumentos coincidentes,\(p=p^{\prime}\), la ecuación (55) se reduce a\[w(p) \equiv w(p, p)=\frac{1}{2 \pi \hbar} \iint d x d x^{\prime} w\left(x, x^{\prime}\right) \exp \left\{-\frac{i p\left(x-x^{\prime}\right)}{\hbar}\right\} .\] Ahora usando la ecuación (29) y luego la ecuación (4.265), esta función puede representarse como\[w(p)=\frac{1}{2 \pi \hbar} \sum_{j} W_{j} \iint d x d x^{\prime} \psi_{j}(x) \psi_{j}^{*}(x) \exp \left\{-\frac{i p\left(x-x^{\prime}\right)}{\hbar}\right\}=\sum_{j} W_{j} \varphi_{j}(p) \varphi_{j}^{*}(p),\] y por lo tanto interpretarse como la densidad de probabilidad del momento de la partícula a su valor\(p\). Ahora, en las variables (51), la Ec. (56) tiene la forma
\[w(p)=\frac{1}{2 \pi \hbar} \iint w\left(X+\frac{\widetilde{X}}{2}, X-\frac{\widetilde{X}}{2}\right) \exp \left\{-\frac{i p \widetilde{X}}{\hbar}\right\} d \widetilde{X} d X .\]Comparando esta igualdad con la definición (50) de la función Wigner, vemos que\[w(P)=\int W(X, P) d X .\] Así, de acuerdo con las ecuaciones (53) y (59), las integrales de la función Wigner sobre la coordenada o el impulso dan las densidades de probabilidad para encontrar el sistema en un cierto valor de la contraparte variable. Este es, por supuesto, el requisito principal para cualquier candidato cuántico-mecánico para el mejor análogo de la densidad de probabilidad clásica,\(w_{\mathrm{cl}}(X, P)\).
Veamos cómo busca la función Wigner los sistemas más simples en equilibrio termodinámico. Para una partícula 1D libre, podemos usar la Eq. (34), ignorando por simplicidad los problemas de normalización:\[W(X, P) \propto \int_{-\infty}^{+\infty} \exp \left\{-\frac{m k_{\mathrm{B}} T \widetilde{X}^{2}}{2 \hbar^{2}}\right\} \exp \left\{-\frac{i P \widetilde{X}}{\hbar}\right\} d \widetilde{X} .\] La integración gaussiana habitual rinde:\[W(X, P)=\text { const } \times \exp \left\{-\frac{P^{2}}{2 m k_{\mathrm{B}} T}\right\} .\] Vemos que la función es independiente de\(X\) (como debería ser para este sistema traduccional-invariante), y coincide con el Gibbs distribución (24). Podríamos obtener el mismo resultado directamente de las estadísticas clásicas. Esto es natural porque como sabemos por la Sec. 2.2, la libre circulación esencialmente no está cuantificada -al menos en términos de su energía e impulso-.
Ahora consideremos un sistema sustancialmente cuántico, el oscilador armónico. Tapando la Eq. (44) a la Ec. (50), para ese sistema en equilibrio térmico es fácil mostrar (y por lo tanto se deja para el ejercicio del lector) que la función Wigner también es gaussiana, ahora en ambos argumentos:\[W(X, P)=\text { const } \times \exp \left\{-C\left[\frac{m \omega_{0}^{2} X^{2}}{2}+\frac{P^{2}}{2 m}\right]\right\},\] aunque el coeficiente ahora\(C\) es diferente de\(1 / k_{\mathrm{B}} T\), y tiende a ese límite sólo a altas temperaturas,\(k_{\mathrm{B}} T \gg \hbar \omega_{0}\). Además, para un estado Glauber, la función Wigner también da un resultado muy plausible distribución\(-\mathrm{a}\) gaussiana similar a la Eq. (62), pero desplazada adecuadamente del origen al punto central del estado\(-\) ver Sec. 5.5. \({ }^{20}\)
Desafortunadamente, para algunos otros posibles estados del oscilador armónico, por ejemplo, cualquier estado puro de Fock con\(n>0\), la función Wigner toma valores negativos en algunas regiones del\([X, P]\) plano\(-\) ver Fig. \(3 .{ }^{21}\)(Tales tramas fueron la base de mis imágenes clásicas, ciertamente muy imperfectas, de los estados de Fock en la Fig. 5.8.)
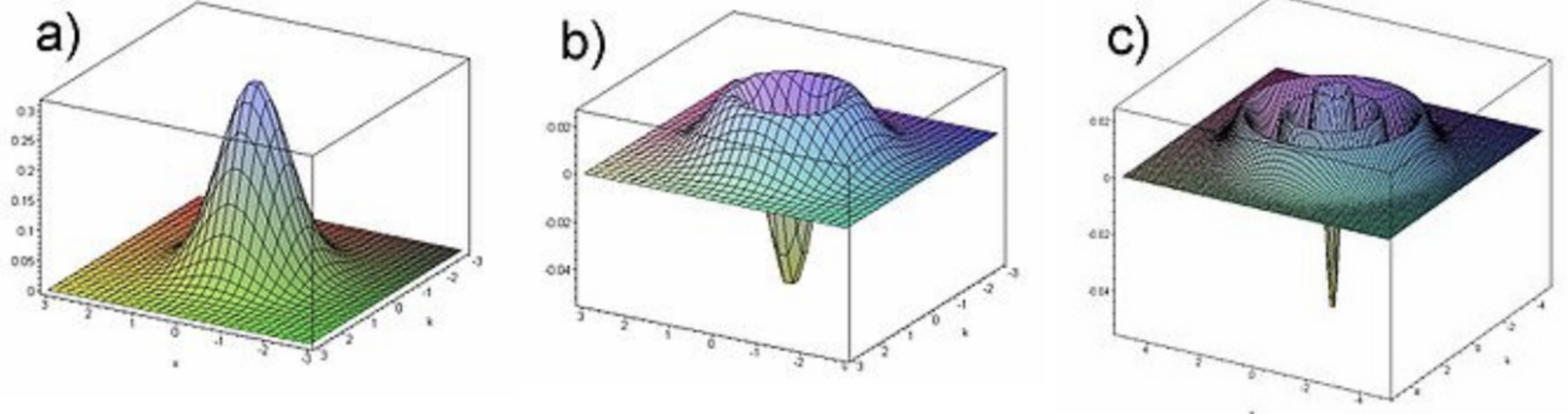
Lo mismo es cierto para la mayoría de los demás sistemas cuánticos y sus estados. En efecto, este hecho podría predecirse con solo mirar la definición (50) aplicada a un estado cuántico puro, en el que la función de densidad puede ser factorizada - ver Ec. (31):\[W(X, P)=\frac{1}{2 \pi \hbar} \int \psi\left(X+\frac{\tilde{X}}{2}\right) \psi^{*}\left(X-\frac{\tilde{X}}{2}\right) \exp \left\{-\frac{i P \tilde{X}}{\hbar}\right\} d \widetilde{X} .\] Cambiando el argumento\(P\) (digamos, en fijo\(X\)), estamos esencialmente cambiando lo espacial” frecuencia” (número de onda) del componente de Fourier del producto de función de onda que estamos calculando, y sabemos que sus imágenes de Fourier normalmente cambian de signo a medida que se cambia la frecuencia. De ahí que las funciones de onda deben tener algunas propiedades de alta simetría para evitar este efecto. En efecto, las funciones gaussianas (describiendo, por ejemplo, los estados Glauber, y en su caso particular, el estado fundamental del oscilador armónico) tienen tal simetría, pero muchas otras funciones no.
De ahí que si la función Wigner se tomara en serio como el análogo cuántico-mecánico de la densidad de probabilidad clásica\(w_{\mathrm{cl}}(X, P)\), necesitaríamos interpretar la probabilidad negativa de encontrar la partícula en ciertos intervalos\(d X d P\) elementales, lo cual es difícil de hacer. Sin embargo, la función se sigue utilizando para una interpretación semicuantitativa de estados mixtos de sistemas cuánticos.
\({ }^{13}\)Por ahora, me enfocaré en un instante de tiempo fijo (digamos,\(t=0\)), y por lo tanto escribiré\(\psi(x)\) en lugar de\(\Psi(x, t)\).
\({ }^{14}\)Este hecho es el origen del nombre de la matriz de densidad.
\({ }^{15}\)Debido a la delta-normalización de la función propia, la matriz de densidad (34) para la partícula libre (y cualquier sistema con un espectro continuo de valores propios) se normaliza como\[\int_{-\infty}^{+\infty} w\left(x, x^{\prime}\right) Z d x^{\prime}=\int_{-\infty}^{+\infty} w\left(x, x^{\prime}\right) Z d x=1 \text {. }\]
\({ }^{16}\)No tendré tiempo para discutir esta técnica y tendré que referir al lector interesado a literatura especial. Probablemente, el texto más famoso de ese campo es A. Abrikosov, L. Gor'kov, e I. Dzyaloshinski, Methods of Quantum Field Theory in Statistical Physics, Prentice-Hall, 1963. (Las reimpresiones posteriores están disponibles en Dover.)
17 Tengo que confesar que esta notación es imperfecta, porque estrictamente hablando,\(w\left(x, x^{\prime}\right)\) y\(w(x)\) son funciones diferentes, y también lo son las funciones\(w\left(p, p^{\prime}\right)\) y\(w(p)\) se utilizan a continuación. En el mundo perfecto, usaría letras diferentes para todas ellas, pero desesperadamente quiero quedarme con "\(w\)" para todas las densidades de probabilidad, y no hay tantas fuentes buenas para esta carta. Permítanme esperar que la diferencia entre estas funciones quede clara a partir de sus argumentos y del contexto.
\({ }^{18}\)Fue introducido en 1932 por Eugene Wigner sobre la base de una transformación general (Weyl-Wigner) sugerida por Hermann Weyl en 1927 y re-derivada en 1948 por Jean Ville sobre una base matemática diferente.
\({ }^{19}\)Dicha función, utilizada para expresar la probabilidad\(d W\) de encontrar el sistema en un área pequeña del plano de fase ya que\(d W=w_{\mathrm{cl}}(X, P) d X d P\), es una noción importante de la estadística clásica (1D) - véase, por ejemplo, SM Sec. 2.1.
\({ }^{20}\)Tenga en cuenta que en la notación de Sec. 5.5, las letras mayúsculas\(X\) y\(P\) significan no los argumentos de la función Wigner, sino las coordenadas cartesianas del punto central (5.102), es decir, la amplitud compleja clásica de las oscilaciones.
\({ }^{21}\)Espectacular mediciones experimentales de esta función (para\(n=0\) y\(n=1\)) fueron realizadas recientemente por E. Bimbard et al., Phys. Rev. Lett. 112, 033601 (2014).


