1.8: Un simple oscilador no lineal

Para ilustrar algunas de las diferencias entre osciladores lineales y no lineales, daremos un ejemplo muy simple de un oscilador no lineal. Considere la siguiente ecuación de movimiento no lineal:

\[m \frac{d^{2}}{d t^{2}} x=\left\{\begin{array}{l}-F_{0} \text { for } x>0 \\ F_{0} \text { for } x<0 \\ 0 \text { for } x=0\end{array}\right.\]

Esto describe una partícula con masa,\(m\), que está sujeta a una fuerza hacia la izquierda,\(−F_0\), cuando la partícula está a la derecha del origen (\(x(t) > 0\)), una fuerza a la derecha,\(F_0\), cuando la partícula está a la izquierda del origen (\(x(t) < 0\)), y ninguna fuerza cuando la partícula está asentada derecha sobre el origen. La energía potencial para este sistema crece linealmente en ambos lados de x = 0. No se puede diferenciar en\(x = 0\), porque la derivada no es continua ahí. Por lo tanto, no podemos expandir la energía potencial (o la fuerza) en una serie de Taylor alrededor del punto\(x = 0\), y los argumentos de (1.21) - (1.24) no se aplican. Es fácil encontrar una solución de (1.120). Supongamos que en el momento\(t = 0\),, la partícula está en el origen pero moviéndose con velocidad positiva,\(v\). La partícula se mueve inmediatamente a la derecha del origen y desacelera con una aceleración constante,\(\frac{−F_0}{m}\), de manera que

\[x(t) = vt - \frac{F_o}{2m}t^2\]

para\(t ≤ τ\).

donde

\[τ=\frac{2mv}{F_o}\]

es el tiempo requerido para que la partícula dé la vuelta y vuelva al origen. En el momento\(t = τ\),, la partícula se mueve hacia la izquierda del origen. En este punto se mueve con velocidad,\(−v\), el proceso se repite para la aceleración negativa\(x\) y positiva\(\frac{F_0}{m}\) Entonces la solución continúa en la forma

\[x(t) = −v(t − τ ) + \frac{F_o}{2m}(t − τ )^2 for τ ≤ t ≤ 2τ\]

Entonces todo el proceso se repite. El movimiento de la partícula, mostrado en la figura 1.15, se ve superficialmente como oscilación armónica, pero la curva es una secuencia de parábolas pegadas entre sí, en lugar de una onda sinusoidal. La ecuación de movimiento, (1.120), es invariante en la traducción del tiempo. Claramente, podemos iniciar la partícula en el origen con velocidad, v, en cualquier momento, t0. La solución entonces se parece a la que se muestra en la figura 1.15 pero traducida en el tiempo por\(t_0\). La solución tiene la forma

\[x_{t0}(t) = x(t-t_o)\]

donde\(x(t)\) está la función descrita por (1.121), (1.123), etc. Esto se muestra en la figura 1.16 para\(t = t_0 = \frac{3τ}{4}\). La curva punteada corresponde a\(t_0 = 0\)

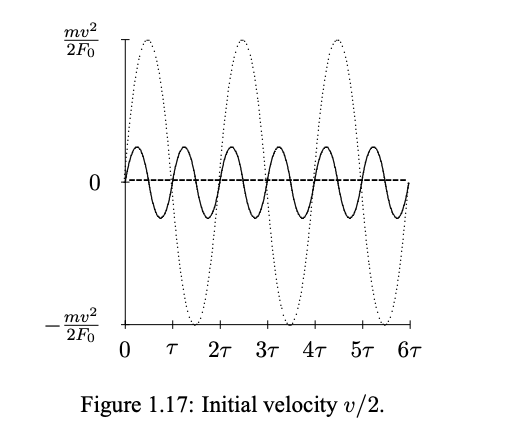
Al igual que el oscilador armónico, este sistema oscila regular e indefinidamente. Sin embargo, en este caso, el periodo de la oscilación, el tiempo que tarda en repetirse, 2τ, depende de la amplitud de la oscilación, o equivalentemente, de la velocidad inicial, v. El periodo es proporcional a v, desde (1.122). El movimiento de la partícula comenzó desde el origen en\(t = t_0\), para una velocidad inicial v/2 se muestra en la figura 1.17. La curva punteada corresponde a una velocidad inicial, v. Mientras que la ecuación no lineal de movimiento, (1.120), es invariante de traslación temporal, la simetría es mucho menos útil porque el sistema carece de linealidad. Desde nuestro punto de vista, lo importante de la linealidad (aparte de que es una buena aproximación en tantos sistemas físicos importantes), es que nos permite elegir una base conveniente para las soluciones a la ecuación del movimiento. Los elegimos para que se comporten simplemente bajo las traducciones de tiempo.

Entonces, debido a la linealidad, podemos construir cualquier solución como una combinación lineal de las soluciones base. En una situación como (1.120), no tenemos esta opción.