2.3: Resonancia

El\(\left(\omega_{0}^{2}-\omega_{d}^{2}\right)^{2}\) término en el denominador de (2.22) va a cero para\(\omega_{d} = \omega_{0}\). Si la amortiguación es pequeña, este comportamiento del denominador da lugar a un enorme incremento en la respuesta del sistema a la fuerza impulsora en\(\omega_{d} = \omega_{0}\). El fenómeno se llama resonancia. La frecuencia angular\(\omega_{0}\) es la frecuencia angular resonante. Cuando\(\omega_{d} = \omega_{0}\), se dice que el sistema está “en resonancia”.

El fenómeno de la resonancia es familiar y espectacularmente importante. Es familiar en situaciones tan simples como construir una gran amplitud en el columpio de un niño suministrando una pequeña fuerza al mismo tiempo en cada ciclo. Sin embargo, por simple que sea, es crucial en muchos dispositivos y muchos experimentos delicados en física. Los fenómenos de resonancia se utilizan ubicuamente para construir una respuesta grande y medible a una perturbación muy pequeña.

Muy a menudo, ignoraremos la amortiguación en las oscilaciones forzadas. Cerca de una resonancia, esto no es una buena idea, porque la amplitud, (2.22), va al infinito en\(\Gamma \rightarrow 0\) cuanto a\(\omega_{d} = \omega_{0}\). Los infinitos no son físicos. Este infinito nunca ocurre en la práctica. Una de dos cosas sucede antes de que la amplitud estalla. O la amortiguación eventualmente no puede ignorarse, por lo que la respuesta se ve como (2.22) para distinto de cero\(\Gamma\), o la amplitud se vuelve tan grande que no se pueden ignorar las no linealidades en el sistema, por lo que la ecuación de movimiento ya no se ve como (2.16).

Trabajo

Es instructivo considerar el trabajo realizado por la fuerza externa en (2.16). Para ello debemos usar la fuerza real, (2.14), y el desplazamiento real (2.25), más que sus complejas extensiones, porque, a diferencia de casi todo lo demás de lo que hablamos, la obra es una función no lineal de la fuerza. La potencia gastada por la fuerza es producto de la fuerza motriz y de la velocidad,\[P(t)=F(t) \frac{\partial}{\partial t} x(t)=-F_{0} \omega_{d} A \cos \omega_{d} t \sin \omega_{d} t+F_{0} \omega_{d} B \cos ^{2} \omega_{d} t .\]

El primer término en (2.26) es proporcional a\(\sin 2 \omega_{d} t\). Por lo tanto, a veces es positivo y a veces negativo. Promedia a cero en cualquier medio periodo completo de oscilación, un tiempo\(\pi / \omega_{d}\), porque\[\int_{t_{0}}^{l_{0}+\pi / \omega_{d}} d t \sin 2 \omega_{d} t=-\left.\frac{1}{2} \cos 2 \omega_{d} t\right|_{t_{0}} ^{t_{0}+\pi / \omega_{d}}=0 .\]

Es por ello\(A\) que se llama la amplitud elástica. Si\(A\) domina, entonces la energía alimentada al sistema en un momento se devuelve en un momento posterior, como en una colisión elástica en mecánica.

El segundo término en (2.26), por otro lado, siempre es positivo. Promedia a\[P_{\text {average }}=\frac{1}{2} F_{0} \omega_{d} B .\]

Es por ello\(B\) que se llama la amplitud de absorción. Mide qué tan rápido es absorbida la energía por el sistema. El poder absorbido\(P_{\text {average }\),, alcanza un máximo en resonancia, a\(\omega_{0} = \omega_{d}\). Este es un diagnóstico que a menudo se utiliza para encontrar resonancias en situaciones experimentales. Tenga en cuenta que la dependencia de\(B\) en\(\omega_{d}\) se ve cualitativamente similar a la de\(P_{\text {average }\), que se muestra en la Figura\( 2.5\) para\(\Gamma = \(\omega_{0} / 2\). Sin embargo, difieren por un factor de\(\omega_{d}\). En particular, el máximo de\(B\) ocurre ligeramente por debajo de la resonancia.

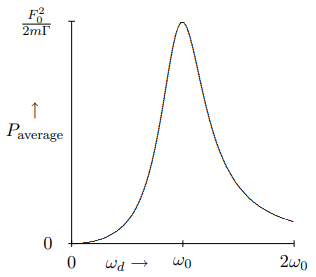
Figura\( 2.5\): La potencia promedio perdida por la fuerza de fricción en función de\(\omega_{d}\) for\(\Gamma=\omega_{0} / 2\).

Ancho de resonancia y vida útil

Tanto la altura como la anchura de la curva de resonancia en la Figura\( 2.5\) están determinadas por el término friccional,\(\Gamma\), en la ecuación de movimiento. La potencia media máxima es inversamente proporcional a\(\Gamma\),\[\frac{F_{0}^{2}}{2 m \Gamma} .\]

El ancho (para altura fija) está determinado por la relación de\(\Gamma\) a\(\omega_{0}\). De hecho, puede verificar que los valores\(\omega_{d}\) para los cuales la pérdida de potencia promedio es la mitad de su valor máximo son\[\omega_{1 / 2}=\sqrt{\omega_{0}^{2}+\frac{\Gamma^{2}}{4}} \pm \frac{\Gamma}{2} .\]

El\(\Gamma\) es el “ancho completo a la mitad del máximo” de la curva de potencia. En Figura\( 2.6\) y Figura\( 2.7\), mostramos la potencia promedio en función de\(\omega_{d}\) para\(\Gamma = \omega_{0} / 4\) y\(\Gamma = \omega_{0}\). La dependencia lineal del ancho\(\Gamma\) es claramente visible. Las líneas punteadas muestran la posición de medio máximo.

Figura\( 2.6\): La potencia promedio perdida por la fuerza de fricción en función de\(\omega_{d}\) for\(\Gamma = \omega_{0} / 4\).

Figura\( 2.7\): La potencia promedio perdida por la fuerza de fricción en función de\(\omega_{d}\) for\(\Gamma = \omega_{0}\).

Esta relación es aún más interesante en vista de la relación entre\(\Gamma\) y la dependencia del tiempo de la oscilación libre. La vida útil del estado en oscilación libre es de orden\(1 / \Gamma\). En otras palabras, el ancho del pico de resonancia en la oscilación forzada es inversamente proporcional a la vida útil del modo normal correspondiente de oscilación libre. Esta relación inversa es importante en muchos campos de la física. Un ejemplo extremo es la física de partículas, donde las partículas de muy corta duración pueden describirse como resonancias. Las ondas mecánicas cuánticas asociadas a estas partículas tienen frecuencias angulares proporcionales a sus energías,\[E=\hbar \omega\]

donde\(\hbar\) está la constante de Planck dividida por\(2 \pi\),\[h \approx 6.626 \times 10^{-34} \mathrm{Js} .\]

Las vidas de estas partículas, algunas tan cortas como\(10^{-24}\) segundos, son demasiado cortas para medirlas directamente. Sin embargo, la corta vida útil se manifiesta en el gran ancho de la distribución de energías de estos estados. Así es como en realidad se deducen las vidas.

Retraso de fase

También podemos escribir (2.25) como\ [x (t) =R\ cos\ izquierda (\ omega_ {d} t-\ theta\ derecha)\)

para\[R=\sqrt{A^{2}+B^{2}}, \quad \theta=\arg (A+i B) .\]

El ángulo de fase,\(\theta\), mide el desfase de fase entre la fuerza externa y la respuesta del sistema. El desfase de tiempo real es\(\theta / \omega_{d}\). El desplazamiento alcanza su máximo un tiempo\(\theta / \omega_{d}\) después de que la fuerza alcanza su máximo.

Tenga en cuenta que a medida que aumenta la frecuencia,\(\theta\) aumenta y el movimiento se queda cada vez más atrás de la fuerza externa. El ángulo de fase\(\theta\),, está determinado por la importancia relativa de la fuerza restauradora y la inercia del oscilador. A bajas frecuencias (en comparación con\(\omega_{0}\)), la inercia (una palabra imprecisa para el\(ma\) término en la ecuación de movimiento) es casi irrelevante porque las cosas se mueven muy lentamente, y el movimiento está muy casi en fase con la fuerza. Mucho más allá de la resonancia, domina la inercia. La masa ya no puede mantenerse al día con la fuerza restauradora y el movimiento está casi\(180^{\circ}\) desfasado con la fuerza. Elaboraremos un ejemplo detallado de esto en la siguiente sección.

El retraso de fase pasa\(\pi / 2\) a través de la resonancia, como se muestra en la gráfica de la Figura\( 2.8\) para\(\Gamma = \omega_{0} / 2\). Un retraso de fase de\(\pi / 2\) es otro diagnóstico de resonancia de uso frecuente.

Figura\( 2.8\): Gráfica del desfase de fase versus frecuencia en un oscilador forzado amortiguado.