3.6: Lista de verificación del capítulo

Ahora deberías ser capaz de:

1. Anote las ecuaciones de movimiento para un sistema con más de un grado de libertad en forma de matriz;
2. Encontrar las\(K\) matrices\(M\) y de la física;
3. Sumar, restar y multiplicar matrices;
4. Encontrar el determinante e inverso de\(2 \times 2\) y\(3 \times 3\) matrices;
5. Encontrar modos normales y frecuencias correspondientes de un sistema con dos grados de libertad, lo que significa encontrar los vectores propios y los valores propios de una\(2 \times 2\) matriz;
6. Comprobar si un vector dado es un modo normal de un sistema con más de dos grados de libertad, y si es así, encontrar la frecuencia angular correspondiente;
7. Dados los modos normales y frecuencias correspondientes y las posiciones y velocidades iniciales de todas las partes en cualquier sistema, encontrar el movimiento de todas las partes en todos los momentos posteriores;
8. * Ir y venir de los modos normales a las coordenadas normales;
9. * Reconstruir la\(M^{-1}K\) matriz a partir de los modos normales y coordenadas normales;
10. * Resolver explícitamente para las oscilaciones libres del sistema con dos grados de libertad con amortiguación y poder analizar sistemas con tres o más grados de libertad si se le dan los vectores propios;
11. * Resolver explícitamente problemas de oscilación forzada con o sin amortiguación para sistemas con tres o menos grados de libertad.

Problemas

3.1. El vector de columna de 3 componentes\(A\), el vector de fila de 3 componentes\(B\) y la\(3 \times 3\) matriz se\(C\) definen de la siguiente manera:\ [A=\ left (\ begin {array} {l}
0\\
2
\\
1\ end {array}\ right),\ quad B=\ left (\ begin {array} {lll}
3 & -2 & 1
\ end {array}\ right),\ quad C=\ left (\ begin {array} {ccc}
1 & 1 & 1\\
0 & -2 & 1\\
2 & 2 & 0
\ end {array}\ right).\]

Calcular los siguientes objetos:\[B A, \quad B C, \quad A B.\]

3.2. Considere la oscilación vertical del sistema de muelles y masas que se muestra a continuación con las constantes de resorte\(K_{A} = 78\),\(K_{B} = 15\) y\(K_{C} = 6\) (todas dinas/cm). Encuentra los modos normales, las coordenadas normales y las frecuencias angulares asociadas. Si el bloque de 1 g. se desplaza hacia arriba 1 cm de su posición de equilibrio con el bloque de 3 g mantenido en su posición de equilibrio y ambos bloques liberados del reposo, describa el movimiento posterior de ambos bloques.

3.3. Considere el sistema de muelles y masas que se muestran a continuación:

con las constantes de resorte en newtones/metro dadas por encima de los resortes y con\(m_{1} = 100\)\(m_{2} = 9\) kg,\(m_{3} = 81\) kg y kg.

1. ¿Cuáles de los siguientes son los modos normales del sistema y cuáles son las frecuencias angulares correspondientes? Tenga en cuenta que la\(M^{-1}K\) matriz puede parecer un poco complicada. \ [\ left (\ begin {array} {l}
   \ psi_ {1}\
   \ psi_ {2}\\
   \ psi_ {3}
   \ end {array}\ right) =\ left (\ begin {array} {c}
   9\\
   0\
   10
   \ end {array}\ right)\ quad\ left (\ begin {array} {c}
   9\\
   60\\
   10
   \ end {array}\ right)\ quad\ left (\ begin {array} {c}
   9\\
   -30\\
   10
   \ end {array}\ right)\ quad\ left (\ begin {array} {c}
   9\\
   30\\
   10
   \ end {array}\ right)\ quad\ left (\ begin {array} {c}
   9\\
   0\
   -10
   \ end {array}\ right)\]
2. Si el sistema se libera del reposo con un desplazamiento inicial como se muestra a continuación (con los desplazamientos medidos en mm), ¿cuánto tiempo tarda en volver primero a su configuración inicial? \ [\ left (\ begin {array} {l}
   \ psi_ {1}\
   \ psi_ {2}\\
   \ psi_ {3}
   \ end {array}\ right) =\ left (\ begin {array} {c}
   9\\
   0\
   10
   \ end {array}\ right)\]

3.4*. Un sistema de cuatro masas conectadas por resortes se describe mediante una matriz de masas,\ [M=\ left (\ begin {array} {llll}
1 & 0 & 0 & 0 &
0\\ 0 & 2 & 0 &
0 & 0 & 0\\ 0 & 0 &
0 & 0 & 0 & 2
\ end {array}\ derecha)\]

y una\(K\) matriz\ [K=\ left (\ begin {array} {cccc}
29 & -10 & -4 & -2\\
-10 & 58 & -14 & -2\\
-4 & -14 & -14 & 31 & -26\
-2 & -26 & 74
\ end {array}\ right)\]

1. ¿Cuáles de los siguientes son los modos normales? \ [\ left (\ begin {array} {l}
   1\\
   2\
   1\\
   1
   \ end {array}\ right)\ left (\ begin {array} {l}
   1\\
   1\
   2\
   1
   \ end {array}\ right)\ quad\ left (\ begin {array} {l}
   2\\
   1\\
   1\\
   1
   \ end {array}\ right)\ quad\ left (\ begin {array} {c}
   2\\
   1\
   -1\\
   -1
   \ end {array}\ derecha)\ quad\ left (\ begin {array} {c}
   4\\
   -3\
   0\\
   1
   \ end {array}\ right)\ quad\ left (\ begin {array} {c}
   0\\
   1\
   -4\\
   3
   \ end {array}\ derecha)\]
2. Para cada modo normal, encuentra la frecuencia angular correspondiente. Pista: esto requiere un poco de aritmética. Si eres perezoso, es posible que quieras usar una calculadora programable o escribir un pequeño programa de computadora para verificarlos por ti. Pero el objetivo de este problema es mostrarte que la cantidad de trabajo requerido para verificar si los vectores son modos normales es realmente pequeña en comparación con el trabajo que implica encontrar los modos desde cero.
3. Si los bloques son liberados del resto de un desplazamiento inicial que es proporcional a\ [\ left (\ begin {array} {c}
   1\\
   1\\
   -1\\
   1
   \ end {array}\ right),\]
   cuyo modo normal no está presente en el moción posterior?
4. Encuentra las coordenadas normales correspondientes a cada uno de los modos normales del sistema.

3.5. Considere las oscilaciones longitudinales del sistema que se muestran a continuación:

Los bloques son libres de deslizarse horizontalmente sin fricción. Los desplazamientos de los bloques desde el equilibrio se miden ambos hacia la derecha. El bloque 1 tiene una masa de 15 gramos y el bloque 2 una masa de 10 gramos. Las constantes de resorte de los resortes se muestran en dinas/cm.

1. Mostrar que la\(M^{-1}K\) matriz de este sistema es\ [M^ {-1} K=\ left (\ begin {array} {cc}
   7 & -6\\
   -9 & 10
   \ end {array}\ right).\]
2. Mostrar que los modos normales son\ [A^ {1} =\ left (\ begin {array} {l}
   1\\
   1
   \ end {array}\ right),\ quad A^ {2} =\ left (\ begin {array} {c}
   2\\
   -3
   \ end {array}\ right).\]
   Encuentra el correspondiente frecuencias angulares,\(\omega_{1}\) y\(\omega_{2}\).

3.6. Considere las oscilaciones longitudinales del sistema que se muestran a continuación:

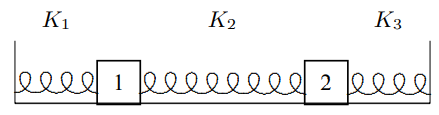
Los bloques son libres de deslizarse horizontalmente sin fricción. Los desplazamientos de los bloques desde el equilibrio se miden ambos hacia la derecha. El bloque 1 tiene una masa de 15 gramos y el bloque 2 una masa de 10 gramos. Las constantes de resorte de los resortes son\(K_{1}\),\(K_{2}\) y\(K_{3}\), como se muestra. Los modos normales de este sistema son\ [A^ {1} =\ left (\ begin {array} {l}
2\\
3
\ end {array}\ right),\ quad A^ {2} =\ left (\ begin {array} {c}
1\\
-1
\ end {array}\ right)\]

con frecuencias correspondientes\[\omega_{1}=1 \mathrm{~s}^{-1}, \quad \omega_{2}=2 \mathrm{~s}^{-1} .\]

1. Si el sistema está en reposo a tiempo\(t = 0\) con desplazamientos\(x_{1}(0)=5 \mathrm{~cm}\)\(x_{2}(0)=0\), o\ [X (0) =\ left (\ begin {array} {l}
   x_ {1} (0)\\
   x_ {2} (0)
   \ end {array}\ right) =\ left (\ begin {array} {l}
   5\\
   0
   \ end { array}\ right)\ mathrm {cm}.\]
   Encuentra el desplazamiento del bloque 2 a la vez\(t = \pi s\).
2. Encontrar\(K_{1}\),\(K_{2}\) y\(K_{3}\).

3.7*. En el sistema de problema (3.5), supongamos que sumergimos el sistema en un fluido amortiguador para que\ [\ Gamma=\ left (\ begin {array} {ll}
\ gamma & 0\\
0 &\ gamma
\ end {array}\ right)\]

con\(\gamma = 1 s^{-1}\), y que se aplique una fuerza externa de la siguiente forma (en dinas):\ [F (t) =f\ cos\ omega t=\ left (\ begin {array} {l}
1\\
0
\ end {array}\ right)\ cos\ omega t.\]

Encuentre y grafique la potencia promedio perdida por la fuerza de fricción en función de\(\omega\) de\(\omega = 0\) a\(10 s^{-1}\).