5.1: Invarianza de la traducción espacial

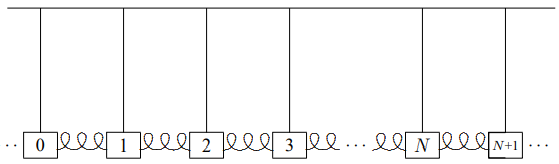
Figura\( 5.1\): Un sistema finito de péndulos acoplados.

El sistema típico de osciladores acoplados que soporta ondas es uno como el sistema de péndulos acoplados\(N\) idénticos que se muestra en la Figura\( 5.1\). Este sistema es una generalización del sistema de dos péndulos acoplados que estudiamos en los capítulos 3 y 4. Supongamos que cada bob de péndulo tiene masa\(m\), cada péndulo tiene longitud\(\ell\), cada resorte tiene constante de resorte\(\kappa\) y la separación de equilibrio entre bobs es\(a\). Supongamos además que no hay fricción y que los péndulos están obligados a oscilar solo en la dirección en la que se estiran los resortes. Nos interesa la libre oscilación de este sistema, sin fuerza externa. Tal oscilación, cuando el movimiento es paralelo a la dirección en la que el sistema se estira en el espacio se llama una “oscilación longitudinal”. Llamar al desplazamiento longitudinal del\(j\) th bob desde el equilibrio (\ psi_ {j}\). Podemos organizar los desplazamientos en un vector,\(\Psi\) (por razones que quedarán claras a continuación, sería confuso usar\(X\), así que elegimos una letra diferente, la letra griega psi, que se ve como\(\psi\) en minúsculas y\(\Psi\) en mayúscula):\ [\ Psi=\ left (\ begin {array} {c}
\ psi_ {1}\\
\ psi_ {2}\\
\ psi_ {3}\\
\ vdots\\
\ psi_ {N}
\ end {array}\ derecha).\]

Entonces las ecuaciones de movimiento (para pequeñas oscilaciones longitudinales) son\[\frac{d^{2} \Psi}{d t^{2}}=-M^{-1} K \Psi\]

donde\(M\) esta la matriz diagonal\(m\) con's a lo largo de la diagonal,\ [\ left (\ begin {array} {ccccc}
m & 0 &\ cdots & 0\\ cdots &
0\\ 0 & m &\ cdots &
0\\ cdots & 0\\ cdots & 0\
\ vdots &\ vdots &\ vdots &\ ddots &\ vdots\\
0 & 0 & 0 &\ cdots & m
\ end {array}\ derecha),\]

y\(K\) tiene elementos diagonales\((m g / \ell+2 \kappa)\), elementos próximos a diagonales\(-\kappa\), y ceros en otra parte,\ [\ left (\ begin {array} {ccccc}
m g/\ ell+2\ kappa & -\ kappa & 0 &\ cdots & 0\
-\ kappa & m g/\ ell+2\ kappa & -\ kappa & -\ kappa &\ cdots & 0\\\
0 & -\ kappa & m g/\ ell+2\ kappa &\ cdots & 0\\
\ vdots &\ vdots &\ vdots &\ vdots &\ ddots &\ vdots &\
vdots\\ 0 & 0 &\ cdots & m g/\ ell+2\ kappa
\ end {array}\ right).\]

El\(- \kappa\) en los elementos próximos a diagonales tiene exactamente el mismo origen que el\(- \kappa\) en la\(2 \times 2 \text { } K\) matriz en (3.78). Describe el acoplamiento de dos bloques vecinos por el muelle. El\((m g / \ell+2 \kappa)\) en la diagonal es análogo al\((m g / \ell+ \kappa)\) en la diagonal de (3.78). La diferencia en el factor de 2 en el coeficiente de\(\kappa\) surge porque hay dos resortes, uno a cada lado, que contribuyen a la fuerza restauradora en cada bloque en el sistema mostrado en la Figura\( 5.1\), mientras que solo hubo uno en el sistema mostrado en la Figura\( 3.1\). Así\(M^{- 1}K\) tiene la forma\ [\ left (\ begin {array} {ccccc}
2 B & -C & 0 &\ cdots & 0\\ -C & 2 B &
-C &\ cdots &\ cdots & 0\\
0 & -C & 2 B &\ cdots & 0\\ vdots &
\ vdots &\ vdots &\ vdots &\ ddots &\ ddots &\ vdots\\
0 & 0 &\ cdots & 2 B
\ end {array}\ derecha)\]

donde\[2 B=g / \ell+2 \kappa / m, \quad C=\kappa / m .\]

Es interesante comparar la matriz, (5.5), con la matriz, (4.43), del capítulo anterior. En ambos casos, los elementos diagonales son todos iguales, debido a la simetría. Lo mismo ocurre con los elementos próximos a la diagonal. Sin embargo, en (5.5), todo el resto de los elementos son cero porque las interacciones son solo entre bloques vecinos más cercanos. Llamamos a tales interacciones “locales”. En (4.43), por otra parte, cada una de las masas interactúa con todas las demás. Utilizaremos la naturaleza local de las interacciones a continuación.

Podríamos intentar encontrar modos normales de este sistema directamente encontrando los vectores propios de\(M^{- 1}K\), pero hay una técnica mucho más fácil y generalmente útil. Podemos dividir la física del sistema en dos partes, la física de los péndulos acoplados y la física de las paredes. Para ello, primero consideramos un sistema infinito sin paredes en absoluto.

Figura\( 5.2\): Pieza de un sistema infinito de péndulos acoplados.

Observe que en la Figura\( 5.2\), no hemos cambiado en absoluto el interior del sistema mostrado\( 5.1\) en la Figura. Acabamos de sustituir las paredes por una continuación del interior.

Ahora podemos encontrar todos los modos del sistema infinito de Figura\( 5.2\) muy fácilmente, haciendo uso de un argumento de simetría. El sistema infinito de Figura\( 5.2\) se ve igual si se traduce, se mueve hacia la izquierda o hacia la derecha por un múltiplo de la separación de equilibrio,\(a\). Tiene la propiedad de “invarianza de la traducción espacial”. La invarianza de la traducción espacial es la simetría del sistema infinito bajo traducciones por múltiplos de\(a\). En este ejemplo, debido a los bloques discretos y la longitud finita de los resortes, la invarianza de traslación espacial es “discreta”. Sólo la traducción por múltiplos integrales de\(a\) dar la misma física. Posteriormente, discutiremos sistemas continuos que tienen invarianza de traducción espacial continua. No obstante, veremos que dichos sistemas pueden ser analizados utilizando las mismas técnicas que introducimos en este capítulo.

Podemos usar la simetría de la invarianza de traslación espacial, así como utilizamos las simetrías de reflexión y rotación discutidas en el capítulo anterior, para encontrar los modos normales del sistema infinito. La invarianza discreta de la traducción espacial del sistema infinito (la simetría bajo traducciones por múltiplos de\(a\)) nos permite encontrar los modos normales del sistema infinito de una manera sencilla.

La mayoría de los modos que encontramos utilizando la invarianza de traslación espacial del sistema infinito de la Figura no\( 5.2\) tendrán nada que ver con el sistema finito que se muestra en la Figura\( 5.1\). Pero si podemos encontrar combinaciones lineales de los modos normales del sistema infinito de Figura\( 5.2\) en los que los bloques 0º y\(N\) + 1º permanecen fijos, entonces deben ser soluciones a las ecuaciones de movimiento del sistema que se muestran en la Figura\( 5.1\). La razón es que las interacciones entre los bloques son “locales” —solo ocurren entre bloques vecinos más cercanos. Así, el bloque 1 sabe lo que está haciendo el bloque 0, pero no lo que está haciendo el bloque −1. Si el bloque 0 es estacionario, bien podría ser una pared porque los bloques del otro lado no afectan al bloque 1 (o a ninguno de los bloques 1 a\(N\)) de ninguna manera. La naturaleza local de la interacción nos permite poner en la física de los muros como condición límite después de resolver el problema infinito. Este mismo truco también nos permitirá resolver muchos otros problemas.

Veamos cómo funciona para el sistema que se muestra en la Figura\( 5.1\). Primero, utilizamos la simetría bajo traducciones para encontrar los modos normales del sistema infinito de Figura\( 5.2\). Al igual que en los dos capítulos anteriores, describimos las soluciones en términos de un vector,\(A\). Pero ahora\(A\) tiene un número infinito de componentes,\(A_{j}\) donde el entero\(j\) va desde\(- \infty\) hasta\(+ \infty\). Es un poco inconveniente escribir este vector infinito hacia abajo, pero podemos representar una parte de él:\ [A=\ left (\ begin {array} {c}\ vdots
\\ A_ {0}\\
A_ {1}\\
A_ {1}\\
A_ {2}\\
A_ {3}\\
\ vdots\\
A_ {N}\\\
A_ {N+1}\\
\ vdots
\ end {array}\ right).\]

Asimismo, la\(M^{- 1}K\) matriz para el sistema es una matriz infinita, no fácilmente anotada, pero cualquier pieza de ella (a lo largo de la diagonal) se parece al interior de (5.5):\ [\ left (\ begin {array} {cccccc}
\ ddots &\ vdots &\ vdots &\ vdots &\ vdots &\ vdots &\ ddots\
\ cdots &\ amp; 2 B & -C & 0 & 0 &\ cdots\
\ cdots & -C & 2 B & -C & 0 &\ cdots\
\ cdots & 0 & -C & 2 B & -C &\ cdots\\ cdots\
\ cdots & 0 & 0 & -C & 2 B &\ cdots\\ cdots\
\ ddots &\ vdots &\ vdots &\ vdots &\ vdots &\ ddots
\ end {array}\ right).\]

Este sistema es “invariante de traslación espacial” porque se ve igual si se mueve a la izquierda una distancia\(a\). Esto mueve el bloque\(j+1\) a donde\(j\) solía estar el bloque, así si hay un modo con componentes\(A_{j}\), debe haber otro modo con la misma frecuencia, representado por un vector,\ (A^ {\ prime} = SA|), con componentes\[A_{j}^{\prime}=A_{j+1} .\]

La matriz de simetría\(S\),, es una matriz infinita con 1s a lo largo de la siguiente a diagonal. Estos son análogos a los 1s a lo largo de la próxima diagonal en (4.40). Ahora, sin embargo, la transformación nunca se cierra sobre sí misma. No hay análogo del 1 en la esquina inferior izquierda de (4.40), porque la matriz infinita no tiene esquina. Queremos encontrar los valores propios y vectores propios de la matriz\(S\), satisfactorios\[A^{\prime}=S A=\beta A\]

o equivalentemente (de (5.9)), los modos en los que\(A_{j}\) y\(A_{j}^{\prime}\) son proporcionales:\[A_{j}^{\prime}=\beta A_{j}=A_{j+1}\]

donde\(\beta\) hay alguna constante distinta de cero. ¹

La ecuación (5.11) se puede resolver de la siguiente manera: Elija\(A_{0} = 1\). Entonces\(A_{1} = \beta\),\(A_{2} = \beta^{2}, etc., so that \(A_{j} = (\beta)^{j}\) para todos los no negativos\(j\). También podemos reescribir (5.11) como\(A_{j-1}=\beta^{-1} A_{j}\), para que\(A_{-1} = \beta_{-1\)\(A_{-2} = \beta_{-2}\), etc. así la solución es\[A_{j}=(\beta)^{j}\]

Ahora que conocemos la forma de los modos normales, es fácil obtener las frecuencias correspondientes actuando sobre (5.12) con la\(M^{-1}K\) matriz, (5.8). Esto da\[\omega^{2} A_{j}^{\beta}=2 B A_{j}^{\beta}-C A_{j+1}^{\beta}-C A_{j-1}^{\beta} ,\]

o insertar (5.13),\[\omega^{2} \beta^{j}=2 B \beta^{j}-C \beta^{j+1}-C \beta^{j-1}=\left(2 B-C \beta-C \beta^{-1}\right) \beta^{j} .\]

Esto es cierto para todos\(j\), lo que demuestra que (5.13) es de hecho un vector propio (ya lo sabíamos por el argumento de simetría, (4.22), pero es bueno verificarlo cuando sea posible), y el valor propio es\[\omega^{2}=2 B-C \beta-C \beta^{-1} .\]

Observe que para casi todos los valores de\(\omega^{2}\), hay dos modos normales, porque podemos intercambiar\(\beta\) y\(\beta^{-1}\) sin cambiar (5.16). Las únicas excepciones son\[\omega^{2}=2 B \mp 2 C ,\]

correspondiente a\(\beta=\pm 1\). El hecho de que haya como máximo dos modos normales para cada valor de\(\omega^{2}\) tendrá una consecuencia dramática. Significa que solo tenemos que lidiar con dos modos normales a la vez para implementar la física del límite. Esta es una característica especial del sistema unidimensional que no es compartida por sistemas bidimensionales y tridimensionales. Como veremos, hace que el sistema unidimensional sea muy fácil de manejar.

Condiciones de Límite

5-1 Ya
hemos resuelto el problema de la oscilación del sistema infinito. Armados con este resultado, podemos volver a poner en la física de los muros. Cualquiera\(\beta\) (excepto\(\beta=\pm 1\)) da un par de modos normales para el sistema infinito de la Figura\( 5.2\). Pero solo los valores especiales de\(\beta\) funcionarán para el sistema finito que se muestra en la Figura\( 5.1\). Para encontrar los modos normales del sistema mostrado en la Figura\( 5.1\), utilizamos (4.56), el hecho de que cualquier combinación lineal de los dos modos normales con la misma frecuencia angular,\(\omega\), es también un modo normal. Si podemos encontrar una combinación lineal que se desvanezca para\(j = 0\) y para\(j = N + 1\), será un modo normal del sistema mostrado en la Figura\( 5.1\). Es la desaparición del modo normal en\(j = 0\) y\(j = N + 1\) que son las “condiciones límite” para este sistema finito particular.

Empecemos por tratar de satisfacer la condición límite en\(j = 0\). Por cada posible valor de\(\omega^{2}\), tenemos que preocuparnos por solo dos modos normales, las dos soluciones de (5.16) para\(\beta\). Siempre y cuando\(\beta \neq \pm 1\), podamos encontrar una combinación que se desvanezca en\(j = 0\); simplemente restar los dos modos\(A^{\beta}\) y\(A^{\beta^{-1}}\) obtener un vector\[A=A^{\beta}-A^{\beta^{-1}} ,\]

o en componentes\[A_{j} \propto A_{j}^{\beta}-A_{j}^{\beta^{-1}}=\beta^{j}-\beta^{-j} .\]

Lo primero que hay que notar sobre (5.19) es que\(A^{j}\) no puede desaparecer para ninguno\(j \neq 0\) a menos que\(|\beta|=1\). Por lo tanto, si queremos tener alguna posibilidad de satisfacer la condición límite en\(j = N + 1\), debemos asumir que\[\beta=e^{i \theta} .\]

Luego de (5.19),\[A_{j} \propto \sin j \theta .\]

Ahora podemos satisfacer la condición de límite en\(j = N + 1\) estableciendo\(A_{N + 1} = 0\). Esto implica\(\sin [(N+1) \theta]=0\), o\[\theta=n \pi /(N+1), \text { for integer } n .\]

Así, los modos normales del sistema mostrado en la Figura\( 5.1\) son\[A_{j}^{n}=\sin \left(\frac{j n \pi}{N+1}\right), \text { for } n=1,2, \cdots N .\]

Otros valores de\(n\) no conducen a nuevos modos, solo repiten los\(N\) modos ya mostrados en (5.23). Las frecuencias correspondientes se obtienen poniendo (5.20) - (5.21) en (5.16), para obtener\[\omega^{2}=2 B-2 C \cos \theta=2 B-2 C \cos \left(\frac{n \pi}{N+1}\right) .\]

A partir de aquí, el análisis del movimiento del sistema es el mismo que para cualquier otro sistema de osciladores acoplados. Como se discute en el capítulo 3, podemos separar un movimiento general y expresarlo como una suma de los modos normales. Esto se ilustra para el sistema de péndulos acoplados en el programa 5-1 en el disco del programa. Lo nuevo de este sistema es la forma en que obtuvimos los modos normales, y su forma peculiarmente simple, en términos de funciones trigonométricas. Vamos a obtener más información sobre el significado de estos modos en la siguiente sección. En tanto, tenga en cuenta la forma en que los modos simples se pueden combinar en el movimiento muy complicado del sistema completo.

___________________
¹ Cero no funciona\(\beta\) porque la ecuación del valor propio no tiene solución.