5.7: Lista de verificación del capítulo

Ahora deberías ser capaz de:

1. Reconocer un sistema finito como parte de un sistema infinito invariante de traslación espacial;
2. Encontrar los modos normales del sistema finito como combinaciones lineales de modos normales del sistema infinito invariante de traslación espacial, consistentes con la física de los límites, imponiendo condiciones de límite;
3. Describir los modos normales de un sistema invariante de traslación espacial en términos de un número de onda angular,\(k\);
4. Encontrar la relación de dispersión que relaciona la frecuencia angular,\(\omega\), con el número de onda angular,\(k\);
5. Resolver problemas de oscilación forzada usando condiciones de límite;
6. Analizar sistemas invariantes de traslación espacial de\(LC\) circuitos acoplados.

Problemas

5.1. Considere las pequeñas oscilaciones longitudinales del sistema que se muestran a continuación:

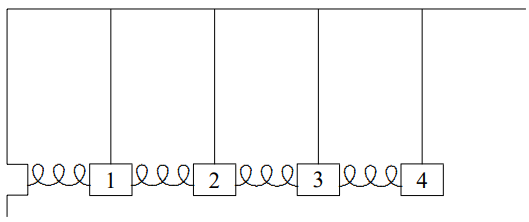
En la imagen de arriba, cada bob tiene masa\(m\), cada péndulo tiene longitud\(\ell\), cada resorte tiene constante de resorte\(\kappa\), y la separación de equilibrio entre bobs es\(a\).

1. Encuentra la\(M^{-1}K\) matriz para este sistema en la base en la que los desplazamientos de los bloques del equilibrio son todos medidos a la derecha y dispuestos en vector de la manera obvia,\ [X (t) =\ left (\ begin {array} {l} x_ {1} (t)\\
   x_ {2} (t)\\
   x_ {3} (t)\\
   x_ {3} (t)\\
   x_ {4} (t)
   \ end {array}\ right).\]
2. Clasificar como VERDADERO o FALSO cada una de las siguientes preguntas sobre los modos normales de este sistema. Si es posible, explique sus respuestas cualitativamente, es decir, en palabras, en lugar de enchufarse a una fórmula, y discuta la generalidad de sus resultados.
   1. En el modo normal con la frecuencia más baja, todos los bloques se mueven en la misma dirección cuando se mueven en absoluto.
   2. En el modo normal con la segunda frecuencia más baja, los bloques 1º y 2º tienen el mismo desplazamiento.
   3. En el modo normal con la frecuencia más alta, los bloques vecinos se mueven en direcciones opuestas cuando se mueven en absoluto.
3. Encuentra las frecuencias angulares de cada uno de los modos normales. Pista: Es posible que desee utilizar la relación de dispersión para péndulos acoplados,\[\omega^{2}=2 B-2 C \cos k a\]

donde\[B=\frac{g}{2 \ell}+\frac{\kappa}{m}, \quad C=\frac{\kappa}{m} .\]

5.2.

En el sistema mostrado anteriormente, todos los bloques tienen masa m y están restringidos para moverse solo horizontalmente. Los resortes largos con seis bucles tienen constante de resorte\(K\). Los resortes más cortos, con tres bucles, tienen constante de resorte\(2K\). Los resortes más cortos, con dos bucles, tienen constante de resorte\(3K\). Como verás en el capítulo 7, esto es lo que esperamos si todos los resortes están hechos del mismo material (ver Figura\( 7.1\)). Encuentra los modos normales del sistema y las frecuencias correspondientes. Asegúrate de justificar cualquier suposición que hagas sobre los modos normales. Pista: Intenta encontrar un sistema infinito con invarianza de traducción espacial que contenga esto de tal manera que puedas poner en la física de las paredes como condición de límite. Otra pista: Esto funciona simplemente solo si los tres resortes de bucle tienen exactamente el doble de la constante de resorte que los resortes largos. Tu respuesta debería explicar por qué.

5.3. En la cadena de cuentas que se muestra a continuación, el intervalo entre cuentas vecinas es\(a\), y la distancia desde las cuentas finales hasta las paredes es\(a / 2\). Todas las cuentas tienen masa\(m\) y están restringidas a moverse solo verticalmente, en el plano del papel.

Mostrar que la física de la pared izquierda se puede incorporar yendo a un sistema infinito y requiriendo la condición límite\(A_{0} = -A_{1}\).

1. Fácil. Encuentre la condición de contorno análoga para el muro derecho.
2. Encuentra los modos normales y las frecuencias correspondientes.

5.4. Considera el siguiente circuito:

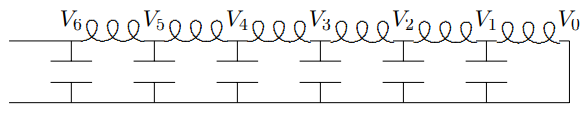
Todos los condensadores tienen la misma capacitancia,\(C \approx 0.00667 \mu F\), y todos los inductores tienen la misma inductancia,\(L \approx 150 \mu H\) y ninguna resistencia. El cable central está conectado a tierra. Este circuito es un análogo eléctrico de los sistemas invariantes de traslación espacial de osciladores mecánicos acoplados que hemos discutido en este capítulo.

Cuando aplica una señal armónicamente oscilante desde un generador de señal a través de un cable coaxial a\(V_{6}\), se inducirán diferentes voltajes oscilantes a lo largo de la línea. Eso es si\[V_{6}(t)=V \cos \omega t ,\]

entonces\(V_{j}(t)\) tiene la forma\[V_{j}(t)=A_{j} \cos \omega t+B_{j} \sin \omega t .\]

Encontrar\(A_{j}\) y\(B_{j}\).