10.3: Ancho de banda, fidelidad e incertidumbre

La relación (10.9) se puede invertir para dar\(C(\omega)\) en términos de\(f(t)\) lo siguiente\[C(\omega)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} d t f(t) e^{i \omega t} .\]

Esta es la “transformada inversa de Fourier”. Es muy importante porque nos permite ir y venir entre la señal y la distribución de frecuencias que contiene. Obtendremos este resultado de dos maneras: primero, con un argumento elegante que volveremos a usar y explicaremos con más detalle en el capítulo 13; a continuación, volviendo a la serie de Fourier, discutida en el capítulo 6 para ondas en una cuerda finita, y tomando el límite ya que la longitud de la cuerda va al infinito.

El argumento elegante va así. Es muy razonable que la integral en (10.37) sea proporcional a\(C(\omega)\) porque si insertamos (10.9) y reorganizamos el orden de integración, obtenemos\[\frac{1}{2 \pi} \int_{-\infty}^{\infty} d \omega^{\prime} C\left(\omega^{\prime}\right) \int_{-\infty}^{\infty} d t e^{i\left(\omega-\omega^{\prime}\right) t} .\]

La\(t\) integral promedia a cero a menos que\(\omega = \omega^{\prime}\). Así, la\(\omega^{\prime}\) integral es simplemente proporcional a\(C(\omega)\) veces un factor constante. El factor de se\(1 / 2 \pi\) puede obtener haciendo algunas integrales explícitamente. Por ejemplo, si\[f(t)=e^{-\Gamma|t|} ,\]

para\(\Gamma>0\) entonces, como mostraremos explícitamente en (10.49) - (10.56), (10.37) rinde\[2 \pi C(\omega)=2 \Gamma /\left(\Gamma^{2}+\omega^{2}\right) ,\]

que a su vez se puede volver a poner en (10.9) para dar (10.39). Para\(t = 0\), la integral se puede hacer por la sustitución trigonométrica\(\omega \rightarrow \Gamma \tan \theta\):\ [\ begin {aligned}
&1=f (0) =e^ {-\ Gamma\ cdot 0} =\ int_ {-\ infty} ^ {\ infty} d\ omega C (\ omega) e^ {-i\ omega\ cdot 0}\\
&=\ frac {1} {\ pi}\ int_ {-\ infty} ^ {\ infty} d\ omega\ frac {\ Gamma} {\ Gamma^ {2} +\ omega^ {2}}\ fila derecha\ frac {1} {\ pi}\ int_ {-\ pi/2} ^ {\ pi/2} d\ theta=1.
\ end {alineado}\]

Para obtener la transformada inversa de Fourier, (10.37), como límite de una serie de Fourier, es conveniente usar una condición límite ligeramente diferente a las que discutimos en el capítulo 6, extremos fijos y extremos libres. En cambio, consideremos una cuerda estirada de\(x=-\pi \ell\) a\(x=\pi \ell\), en la que asumimos que el desplazamiento de la cuerda desde el equilibrio en\(x=\pi \ell\) es el mismo que el desplazamiento en\(x=-\pi \ell\), ²\[\psi(-\pi \ell, t)=\psi(\pi \ell, t) .\]

El requisito, (10.42), se denomina “condiciones de límite periódicas”, porque implica que la función\(\psi\) que describe el desplazamiento de la cadena es periódica en\(x\) con punto\(2 \pi \ell\). Los modos normales del sistema infinito que satisfacen (10.42) son\[e^{i n x / \ell} ,\]

para entero\(n\), porque cambiar\(x\) por\(2 \pi \ell\) en (10.43) solo cambia la fase de la exponencial por\(2 \pi\). Así, si\(\psi(x)\) es una función arbitraria satisfactoria\(\psi(-\pi \ell)=\psi(\pi \ell)\), deberíamos poder expandirla en los modos normales de (10.43),\[\psi(x)=\sum_{n=-\infty}^{\infty} c_{n} e^{-i n x / \ell} .\]

Así mismo, para una función\(f(t)\), satisfactoria\(f(-\pi T)=f(\pi T)\) por algún tiempo grande\(T\), esperamos poder expandirla de la siguiente manera\[f(t)=\sum_{n=-\infty}^{\infty} c_{n} e^{-i n t / T} ,\]

donde hemos cambiado el signo en el exponencial para estar de acuerdo (10.9). Vamos a demostrar que como\(T \rightarrow \infty\), esto se convierte en equivalente a (10.9).

La ecuación (10.44) es el análogo de (6.8) para la condición de límite, (10.42). La suma va de\(-\infty\) a\(\infty\) en lugar de 0 a\(\infty\) porque los modos en (10.43) son diferentes para\(n\) y\(-n\). Para esta serie de Fourier, la inversa es\[c_{m}=\frac{1}{2 \pi T} \int_{-\pi T}^{\pi T} d t e^{i m t / T} f(t)\]

donde hemos usado la identidad\ [\ frac {1} {2\ pi T}\ int_ {-\ pi T} ^ {\ pi T} d t e^ {i m t/T} e^ {-i n t/T} =\ left\ {\ begin {array} {l}
1\ text {for} m=n,\\
0\ text {for} m\ neq n.
\ end {array}\ derecho.\]

Ahora supongamos que\(f(t)\) va a 0 para grande\(|t|\) (tenga en cuenta que esto es consistente con la condición de límite periódico (10.42)) lo suficientemente rápido para que la integral in (10.46) esté bien definida como\(T \rightarrow \infty\) para todos\(m\). Entonces por el factor de\(1/T\) in (10.47), el\(c_{n}\) todo va a cero como\(1/T\). Así debemos multiplicar\(c_{n}\) por\(T\) para conseguir algo finito en el límite. Comparando (10.45) con (10.9), vemos que debemos tomar\(\omega\) para ser\(n/T\).

Así la relación, (10.45), es un análogo de la integral de Fourier, (10.9) donde la correspondencia es\ [\ begin {aligned}
T &\ rightarrow\ infty\
\\ frac {n} {T} &\ rightarrow\ omega\
c_ {n} T &\ rightarrow C (\ omega).
\ end {alineado}\]

En el límite,\(T \rightarrow \infty\), la suma se convierte en una integral sobre\(\omega\).

Multiplicar ambos lados de (10.46) por\(T\), y hacer la sustitución de (10.48) da (10.37).

Ejemplo Solvable

Para la práctica en el manejo de la integración de funciones complejas, haremos la integración que lleva a (10.40) en detalle gory, con todos los pasos. \[C(\omega)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} d t e^{-\Gamma|t|} e^{i \omega t} .\]

Primero nos deshacemos del valor absoluto —\[=\frac{1}{2 \pi} \int_{0}^{\infty} d t e^{-\Gamma t} e^{i \omega t}+\frac{1}{2 \pi} \int_{-\infty}^{0} d t e^{\Gamma t} e^{i \omega t}\]

y escribir la segunda integral como integral de 0 a\(\infty\) —\[=\frac{1}{2 \pi} \int_{0}^{\infty} d t e^{-\Gamma t} e^{i \omega t}+\frac{1}{2 \pi} \int_{0}^{\infty} d t e^{-\Gamma t} e^{-i \omega t}\]

\[=\frac{1}{2 \pi} \int_{0}^{\infty} d t e^{-\Gamma t} e^{i \omega t}+\text { complex conjugate, }\]

pero sabemos diferenciar incluso exponenciales complejos (ver la discusión de (3.108)), así podemos escribir\[\frac{\partial}{\partial t}\left(e^{-\Gamma t} e^{i \omega t}\right)=(-\Gamma+i \omega) e^{-\Gamma t} e^{i \omega t} .\]

Así\[\int_{0}^{\infty} d t e^{-\Gamma t} e^{i \omega t}=\frac{1}{-\Gamma+i \omega} \int_{0}^{\infty} d t \frac{\partial}{\partial t}\left(e^{-\Gamma t} e^{i \omega t}\right)\]

o, utilizando el teorema fundamental del cálculo integral,\[=\left.\frac{1}{-\Gamma+i \omega}\left(c^{-\Gamma t} c^{i \omega t}\right)\right|_{t=0} ^{\infty}=\frac{1}{\Gamma-i \omega} .\]

Esta función de\(\omega\) se llama “polo”. Si bien la función se comporta perfectamente bien de verdad\(\omega\), explota para\(\omega=-i \Gamma\), lo que se llama la posición del polo en el plano complejo. Ahora solo tenemos que agregar el conjugado complejo para obtener\ [\ begin {reunió}
C (\ omega) =\ frac {1} {2\ pi}\ left (\ frac {1} {\ gamma-i\ omega} +\ frac {1} {\ gamma+i\ omega}\ right)\\
=\ frac {1} {2\ pi}\ left (\ gamma+i\ omega} MA+i\ omega} {\ Gamma^ {2} +\ omega^ {2}} +\ frac {\ gamma-i\ omega} {\ Gamma^ {2} +\ omega^ {2}}\ derecha ) =\ frac {1} {2\ pi}\ frac {2\ Gamma} {\ Gamma^ {2} +\ omega^ {2}}
\ fin {reunidos}\]

que es (10.40). Ya comprobamos, en (10.41), que el factor de tiene\(1 / 2 \pi\) sentido.

El par (10.39) - (10.40) ilustra un hecho muy general sobre las señales y sus espectros de frecuencia asociados. En Figura\( 10.4\) trazamos\(f(t)\) para\(\Gamma=0.5\) y\(\Gamma=2\) y en Figura\( 10.5\), trazamos\(C(\omega)\) para los mismos valores de\(\Gamma\). Observe que a medida que\(\Gamma\) aumenta, la señal llega a tener un pico más brusco cerca\(t = 0\) pero el espectro de frecuencia se extiende. Y a la inversa si ¡es pequeño por lo que\(C(\omega)\) se encuentra muy cerca de su punto máximo\(\omega = 0\), entonces\(f(t)\) se esparce en el tiempo. Este comportamiento complementario es general. Para resolver tiempos cortos, se necesita un amplio espectro de frecuencias.

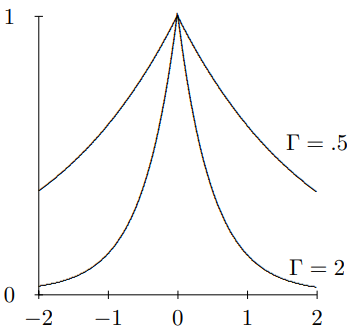
Figura\( 10.4\):\(f(t)=e^{-|\Gamma t|}\) para\(\Gamma=0.5\) y\(\Gamma=2\).

Figura\( 10.5\):\(C(\omega)\) para los mismos valores de\(\Gamma\).

Generalidades Amplias

Podemos afirmar este hecho de manera muy general utilizando una definición matemática precisa de la propagación de la señal en el tiempo y la dispersión del espectro en frecuencia.

Definiremos la intensidad de la señal para que sea proporcional a\(|f(t)|^{2}\). Luego, podemos definir el valor promedio de cualquier función\(g(t)\) ponderada con la intensidad de la señal de la siguiente manera\[\langle g(t)\rangle=\frac{\int_{-\infty}^{\infty} d t g(t)|f(t)|^{2}}{\int_{-\infty}^{\infty} d t|f(t)|^{2}} .\]

Esto pondera\(g(t)\) más cuando la señal es más intensa.

Por ejemplo,\(\langle t\rangle\) es el tiempo promedio, ese es el valor de tiempo alrededor del cual la señal es más intensa. Entonces\[\left\langle[t-\langle t\rangle]^{2}\right\rangle \equiv \Delta t^{2}\]

mide la desviación cuadrática media del tiempo promedio, por lo que es una medida de la dispersión de la señal.

Podemos definir el valor promedio de una función de\(\omega\) manera análoga integrando sobre la intensidad del espectro de frecuencias. Pero aquí está el truco. Debido a (10.9) y (10.37), podemos ir y venir entre\(f(t)\) y\(C(\omega)\) a voluntad. Llevan la misma información. Deberíamos ser capaces de calcular promedios de funciones de\(\omega\) mediante el uso de una integral over\(t\). Y efectivamente, podemos. Considerar la integral\[\int_{-\infty}^{\infty} d \omega \omega C(\omega) e^{-i \omega t}=i \frac{\partial}{\partial t} \int_{-\infty}^{\infty} d \omega C(\omega) e^{-i \omega t}=i \frac{\partial}{\partial t} f(t) .\]

Esto demuestra que multiplicar\(C(\omega)\) por\(\omega\) equivale a diferenciar lo correspondiente\(f(t)\) y multiplicar por\(i\).

Así podemos calcular\(\langle\omega\rangle\) como\[\langle\omega\rangle=\frac{\int_{-\infty}^{\infty} d t f(t)^{*} i \frac{\partial}{\partial t} f(t)}{\int_{-\infty}^{\infty} d t|f(t)|^{2}} ,\]

y\[\Delta \omega^{2} \equiv\left\langle[\omega-\langle\omega\rangle]^{2}\right\rangle=\frac{\int_{-\infty}^{\infty} d t\left|\left(i \frac{\partial}{\partial t}-\langle\omega\rangle\right) f(t)\right|^{2}}{\int_{-\infty}^{\infty} d t|f(t)|^{2}} .\]

\(\Delta \omega\)es una medida de la dispersión del espectro de frecuencias, o el “ancho de banda”.

Ahora podemos exponer y probar el siguiente resultado:\[\Delta t \cdot \Delta \omega \geq \frac{1}{2} .\]

Una consecuencia importante de este teorema es que para un ancho de banda dado\(\Delta \omega\),, la propagación en el tiempo de la señal no puede ser arbitrariamente pequeña, sino que está delimitada por\[\Delta t \geq \frac{1}{2 \Delta \omega} .\]

Cuanto menor sea el valor mínimo posible de\(\Delta t\) que puedas enviar, mayor será la “fidelidad” que puedas lograr. Más pequeño\(\Delta t\) significa que puedes enviar señales con detalles más nítidos. Pero (10.63) significa que cuanto menor es el ancho de banda, mayor es el mínimo\(\Delta t\) y menor es la fidelidad.

Para probar (10.62) considerar la función ³\[\left([t-\langle t\rangle]-i \kappa\left[i \frac{\partial}{\partial t}-\langle\omega\rangle\right]\right) f(t)=r(t),\]

que depende del parámetro completamente libre\(\kappa\). Ahora mira la relación\[\frac{\int_{-\infty}^{\infty} d t|r(t)|^{2}}{\int_{-\infty}^{\infty} d t|f(t)|^{2}} .\]

Esta relación es obviamente positiva, porque los integrandos tanto del numerador como del denominador son positivos. Lo que vamos a hacer es elegir\(\kappa\) inteligentemente, de modo que el hecho de que la proporción sea positiva nos diga algo interesante.

Primero, vamos a simplificar (10.65). En los términos en (10.65) que involucran derivados de\(f(t)^{*}\), podemos integrarnos por partes (y desechar los términos límite porque suponemos que\(f(t)\) va a cero en el infinito) para que los derivados actúen sobre\(f(t)\). Entonces (10.65) se convierte\[\Delta t^{2}+\kappa^{2} \Delta \omega^{2}+\kappa \frac{\int_{-\infty}^{\infty} d t f(t)^{*}\left(t \frac{\partial}{\partial t}-\frac{\partial}{\partial t} t\right) f(t)}{\int_{-\infty}^{\infty} d t|f(t)|^{2}} .\]

Todos los demás términos cancelan. Pero\[\frac{\partial}{\partial t}[t f(t)]=f(t)+t \frac{\partial}{\partial t} f(t) .\]

Así el último término en (10.66) es justo\(\kappa\), y (10.65) se convierte\[\Delta t^{2}+\kappa^{2} \Delta \omega^{2}-\kappa .\]

(10.68) es claramente mayor o igual a cero para cualquier valor de\(\kappa\), porque es una relación de integrales positivas. Para obtener la mayor cantidad de información del hecho de que es positiva, debemos elegir\(\kappa\) para que (10.65) (=( 10.68)) sea lo más pequeño posible. En otras palabras, debemos encontrar el valor de\(\kappa\) que minimiza (10.68). Si diferenciamos (10.68) y establecemos el resultado a cero, encontramos\[\kappa_{\min }=\frac{1}{2 \Delta \omega^{2}} .\]

Ahora podemos enchufar esto de nuevo en (10.68) para encontrar el mínimo, que sigue siendo mayor o igual a cero. Es\[\Delta t^{2}-\frac{1}{4 \Delta \omega^{2}} \geq 0\]

que inmediatamente rinde (10.62).

La ecuación (10.62) aparece en muchos lugares de la física. Un ejemplo sencillo es el ancho de banda en las transmisiones de radio AM. Una estación AM comercial típica emite en una banda de frecuencia alrededor de 5000 ciclos/s (5 kc) a cada lado de la frecuencia de onda portadora. Así\[\Delta \omega=2 \pi \Delta \nu \approx 3 \times 10^{4} \mathrm{~s}^{-1} ,\]

y no pueden enviar señales que separen tiempos con menos de unos\(\times 10^{-5}\) segundos de diferencia. Esto es lo suficientemente bueno para hablar y aceptable para algo de música.

Un famoso ejemplo de (10.62) proviene de la mecánica cuántica. Existe una relación completamente análoga entre la dispersión espacial de un paquete de ondas\(\Delta x\), y la dispersión de\(k\) valores requeridos para producirlo,\(\Delta k\):\[\Delta x \cdot \Delta k \geq \frac{1}{2}\]

En mecánica cuántica, el impulso de una partícula está relacionado con el\(k\) valor de la onda que la describe por\[p=\hbar k ,\]

donde\(\hbar\) está la constante de Planck\(h\) dividida por\(2 \pi\). Así (10.72) implica\[\Delta x \cdot \Delta p \geq \frac{\hbar}{2} .\]

Esta es la afirmación matemática del hecho de que la posición y el impulso de una partícula no se pueden especificar simultáneamente. Esta es la relación de incertidumbre de Heisenberg.

___________________
² Un ejemplo de un sistema físico con este tipo de condición límite sería una cuerda estirada alrededor de un cilindro sin fricción con radio\(\ell\) y (por lo tanto) circunferencia\(2 \pi \ell\). Entonces (10.42) sería cierto porque\(x=-\pi \ell\) describe el mismo punto en la cadena que\(x=\pi \ell\).
³ Este es un truco tomado de un análisis similar que lleva al principio de incertidumbre de Heisenberg en la mecánica cuántica. No te preocupes si no te resulta obvio de dónde viene. Lo importante es el resultado.