11.6: Lentes y Óptica Geométrica

Óptica Geométrica

La idea de la óptica geométrica es comprender los efectos de la refracción y la reflexión sobre los haces de luz, ignorando los efectos de la difracción. Esto es realmente solo la ley y geometría de Snell. Una aplicación de estas ideas será en la discusión del arco iris en la siguiente sección. Ahí usamos lo que se llama “trazado de rayos” que como su nombre indica es simplemente hacer un seguimiento de lo que hace cada rayo de luz a medida que pasa por la gota. Una gota esférica es una “lente gruesa”. Obviamente, no tiene sentido en el que una esfera pueda ser considerada como “delgada”. En esta sección vamos a ver cómo dar una descripción aproximada más simple de lo que hace una “lente delgada”. De hecho, si estuviéramos diseñando un instrumento óptico muy preciso, seguiríamos usando el trazado de rayos para obtener los detalles finos correctos. Pero el análisis de lente delgada es un buen punto de partida aproximado y nos ayudará a entender lo que está sucediendo en algunas situaciones importantes.

Técnicamente, lo que significa “delgado” en este contexto es que si un haz de luz estrecho aproximadamente perpendicular al plano de la lente entra en la lente en algún punto de un lado, sale aproximadamente en el mismo punto del otro lado. Si ignoramos el pequeño cambio de posición, esto simplifica el análisis y nos da la fórmula de lente delgada.

Lentes esféricas delgadas

En el Capítulo 11, derivamos la fórmula para el cambio angular en un haz de luz estrecho (estamos ignorando la difracción) debido a un prisma. El análisis se utiliza la construcción geométrica

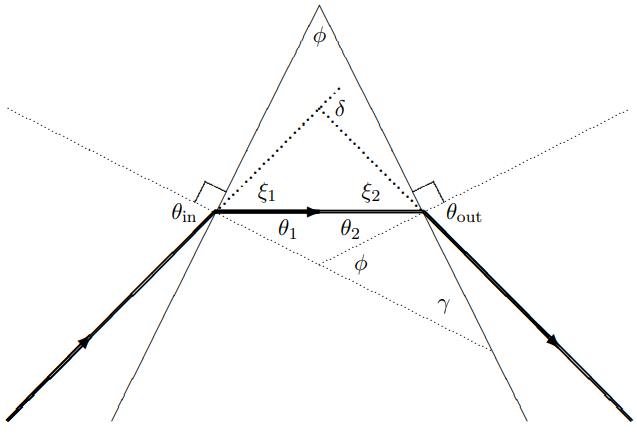
Figura\( 11.26\):

se muestra en la Figura\( 11.26\) y da\ [\ begin {recopilada}
\ delta=\ theta_ {\ text {in}} +\ theta_ {\ text {out}} -\ theta_ {1} -\ theta_ {2}\
\\ approx n\ left (\ theta_ {1} +\ theta_ {2}\ nderecha) -\ phi\ approx (-1)\ phi
\ fin {reunidos}\]

donde el primero es exacto y el segundo sigue en el límite en el que los\(\theta\) ángulos son pequeños. En este límite, la deflexión angular es independiente del ángulo entrante.

lentes y ángulos pequeños

Podemos usar este resultado para entender cómo una lente enfoca la luz. Una lente es un dispositivo en el que el cambio angular dado al haz es proporcional a la distancia desde el eje para pequeños ángulos y distancias —\[\delta \approx h / f\]

donde\(f\) es la longitud. Esto es aproximadamente cierto para una pieza de vidrio con superficies que son partes de esferas. En la Figura\( 11.27\) hay un diagrama que muestra cómo funciona esto para una lente que es plana por un lado y una esfera parcial con radio\(r_{1}\) en el otro. En el diagrama, | (\ theta_ {1}\) es el ángulo del “prisma efectivo” visto por la parte de un haz a\(h\) distancia del eje. Debe quedar claro a partir de la cifra que si\(\theta_{1}\) es pequeño, es proporcional a\(h\). \[\theta_{1} \approx \sin \theta_{1}=\frac{h}{r_{1}}\]

Figura\( 11.27\):

Más a menudo, la lente está curvada en ambos lados. Si los radios son\(r_{1}\) y\(r_{2}\), el resultado se parece a Figura\( 11.28\). La figura\( 11.28\) muestra el haz en la punta de la lente para mayor comodidad, pero como

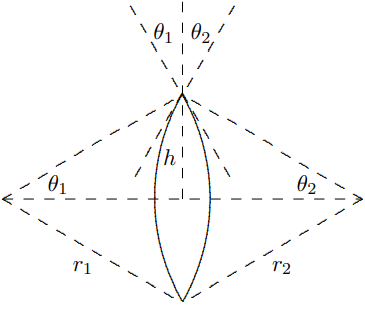
Figura\( 11.28\):

el diagrama anterior debe dejar claro,\(\theta_{1}+\theta_{2}\) es el ángulo de “prisma efectivo” para cualquier\(h\). La figura también exagera la curvatura de los dos lados, de manera que la lente que se muestra en la foto no es realmente “delgada”. Una lente delgada se parece más a Figura\( 11.29\). Esto es importante porque si la lente es gorda, la altura no\(h\) está muy bien definida porque si la luz dentro de la lente no es horizontal, podríamos tener una\(h\) donde la luz entra en la lente y una muy diferente\(h\) donde salga. Pero si la lente es delgada y si los rayos de luz no están muy lejos de la perpendicular, esta ambigüedad en

Figura\( 11.29\):

\(h\)puede ignorarse al igual que otras correcciones a las relaciones de ángulo pequeño (como\(\sin \theta \approx \theta\)).

Armando la geometría de la Figura\( 11.28\) con la fórmula para\(\delta\) en un prisma, obtenemos la constante\(f\) para una lente esférica delgada:\ [\ begin {reunió}\ delta =( n-1)
\ left (\ theta_ {1} +\ theta_ {2}\ right)\\ approx (n-1)\ left (
\ frac {h} {r_ {1}} +\ frac {h} {r_ {1} +\ frac {h} {r_ {h} _ {2}}\ derecha) = \ frac {h} {f}
\ fin {reunidos}\]

y así\[\frac{1}{f}=(n-1)\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}\right)\]

Esto se llama la “fórmula del fabricante de lentes”

Figura\( 11.30\):

Una lente de este tipo enfoca rayos de luz paralelos, como se muestra en la Figura\( 11.30\). Esto funciona porque\(\delta \approx h / f\) como se muestra en la Figura\( 11.31\). Los rayos paralelos en cualquier ángulo se enfocan en un “plano focal” a una\(f\) distancia de la lente como se muestra en la Figura\( 11.32\). La manera analítica de explicar cómo funciona esto es señalar que la diferencia en las pendientes de los rayos en los dos

Figura\( 11.31\):

Figura\( 11.32\):

lados de la lente es proporcional a la altura. Así el en este caso, debido a que las pendientes de un lado son las mismas, la diferencia de pendientes en el otro lado es proporcional a la diferencia de altura, y eso significa que todas se juntan a la misma\(x\).

Otra forma de ver que este enfoque debe funcionar se ilustra en\(Figures \text { } 11.33\) y\(11.34\). Tenga en cuenta que si los rayos paralelos están entrando en ángulo\(\delta_{i}\), el rayo una distancia\(h_{i}=\delta f\) por encima del centro de la lente se dobla a la horizontal, como se muestra en la Figura\( 11.33\) con la línea continua. Entonces para los rayos a ambos lados de ese rayo (mostrados como líneas discontinuas), debido a que la dependencia de la flexión de la altura en la lente es lineal, la curva angular total,\(\delta_{i}+\delta_{o}\) se\(f\) multiplica por la distancia total desde el centro,\(h_{i}+h_{o}\), pero luego\(h_{o}=\delta_{o} f\), que es la condición para enfoque. Esto se ilustra en la Figura\( 11.34\).

Figura\( 11.33\):

Figura\( 11.34\):

Para un haz de rayos paralelos en cualquier ángulo, se puede determinar dónde golpean el plano focal trazando cualquier rayo, siendo el más fácil el que pasa por el centro de la lente, que no está doblado en absoluto, como se muestra en la Figura\( 11.35\). Se puede pensar que los rayos paralelos (una parte de una onda plana —sabemos que esto es imposible, pero estamos ignorando la difracción) provienen de una fuente puntual en el infinito. Si hay una fuente puntual más cerca de la lente, se enfoca más lejos. Ahora juega con la animación LENS.EXE.

Figura\( 11.35\):

Para encontrar la relación entre\(d_{1}\) y\(d_{2}\), considere el diagrama en la Figura\( 11.37\) — la suma de los ángulos de deflexión en los dos lados es igual a\(\delta\):\[\delta_{1}+\delta_{2}=\delta\]

Figura\( 11.36\):

Figura\( 11.37\):

que para ángulos pequeños es equivalente a\[\frac{h}{d_{1}}+\frac{h}{d_{2}}=\frac{h}{f}\]

o\[\frac{1}{d_{1}}+\frac{1}{d_{2}}=\frac{1}{f}\]

Esto se llama la “fórmula de lente delgada”.

Hasta el momento, hemos discutido lentes “convergentes” o “convexas” para las cuales\(f\) es positiva, pero también hay lentes “divergentes” o “cóncavas”, para lo cual\(f\) es negativo. En este caso, los rayos paralelos no son focos, sino desenfocados, y parecen divergir de un plano a una distancia −\(f\) (que es un número positivo) más allá de la lente, como se muestra en la Figura\( 11.38\): El punto a partir del cual

Figura\( 11.38\):

los rayos salientes divergen se llama una “imagen virtual”. En este caso se trata de una imagen virtual del punto en el infinito. En la Figura\( 11.39\) se muestra el efecto de una lente cóncava sobre una fuente puntual. Nuevamente hay una imagen virtual. Aquí la fórmula de lente delgada sigue satisfecha, pero ambas\(f\) y\(d_{2}\) son negativas.

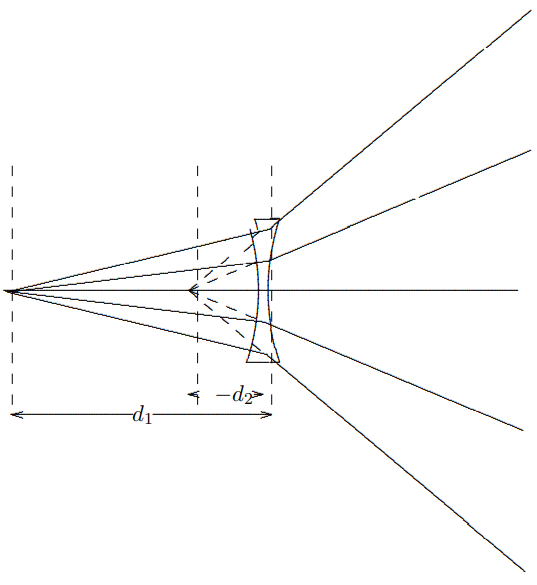
Figura\( 11.39\):

Imágenes

La propiedad de enfoque de una lente se puede utilizar para proyectar una imagen de un objeto sobre una superficie, como se muestra en la Figura\( 11.40\). Lo que está sucediendo es que la luz se avivaba a partir de cada punto

Figura 11.40:

el objeto se enfoca de nuevo a un solo punto en la pantalla. Como en\(Figures \text { } 11.36\) y\(11.37\), las distancias satisfacen la fórmula de lente delgada,\[\frac{1}{d_{1}}+\frac{1}{d_{2}}=\frac{1}{f}\]

Esto te dirá dónde poner la pantalla. Obsérvese también que es fácil ver en qué parte de la pantalla aparece la imagen de un punto particular en el objeto debido a que un rayo de luz que pasa por el centro de la lente no se desvía en absoluto (también usamos esto para rayos paralelos arriba de la Figura\( 11.35\)). Esta geometría más simple implica entonces que la relación entre el tamaño de la imagen y el tamaño del objeto es\(d_{2} / d_{1}\). \[\frac{\text { size of image }}{\text { size of object }}=\frac{d_{2}}{d_{1}}\]

Si se quita la pantalla en Figura,\( 11.40\) se puede ver que la luz a la derecha de donde estaba la pantalla es una copia de la luz proveniente del objeto, pero al revés, y cambiada de tamaño por\(d_{2} / d_{1}\). Si has jugado con lentes, ya lo sabes.

Observe que (11.153) implica que ni\(d_{1}\) ni\(d_{2}\) puede ser menos eso\(f\). Si acercas demasiado el objeto a la lente, no obtienes una imagen real en el otro lado. En cambio,\(d_{2}\) se vuelve negativo y se obtiene una “imagen virtual” en el mismo lado de la lente que el objeto, y la luz a la derecha de la lente es divergente como si viniera de la imagen virtual. Esta situación se ilustra en la Figura\( 11.41\). Como discutiremos más adelante, así es como funciona una lupa.

Figura\( 11.41\):

La formación de la imagen ilustrada en Figura\( 11.40\) es lo que sucede en una cámara, y en tu propio globo ocular. La lente enfoca la luz desde puntos externos hacia puntos en la película o tu retina. Por supuesto, la retina no es en realidad un plano. Por la misma razón, tu lente ocular no es una lente esférica, sino alguna forma más complicada en su lugar. El trazado de rayos se ha hecho por evolución, sin embargo, para que los objetos en un plano se enfoquen adecuadamente sobre la retina.

Debido a que la distancia desde tu lente ocular a tu retina está fijada por la geometría de tu ojo, debes poder ajustar la forma de tu lente. Al hacerlo, puedes cambiar la distancia focal de tu lente y así cambiar la distancia a la que los puntos están perfectamente enfocados (esto se llama “acomodación”).

La formación de una imagen en tu retina se ilustra en el diagrama de la Figura\( 11.42\). Nuevamente como en\( 11.40\) la Figura la imagen está al revés. No puedes enfocarte en objetos que son demasiado

Figura\( 11.42\):

cerca de tu lente ocular porque la cantidad de acomodación que puedes hacer es limitada. Si acercas demasiado el objeto que la distancia focal más pequeña que tu lente ocular puede producir, la imagen real está más allá de tu retina, el objeto se verá borroso, como se muestra en la Figura\( 11.43\).

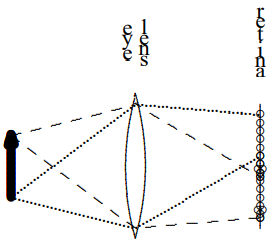
Figura\( 11.43\):

Una lupa funciona al permitirle producir una imagen más grande del objeto en su retina. Esto lo hace de dos maneras, ambas se ilustran en el diagrama de la Figura\( 11.44\) (con menos rayos de luz mostrados ahora porque los diagramas están demasiado ocupados).

Figura\( 11.44\):

Obviamente, la imagen es más grande. Pero tenga en cuenta también que la lupa cambia la cantidad de acomodación requerida por su lente ocular. Tu ojo en realidad se está enfocando en la imagen virtual que está mucho más lejos, y eso es más fácil. Así, cuando miras un objeto en una lupa, puedes acercarlo mucho más a tu ojo y luego podrías sin el cristal. Esto aumenta aún más el efecto de aumento, porque los objetos más cercanos se ven más grandes. En este diagrama también se puede ver un tercer efecto salutario de la lupa — más de la luz del objeto llega a tu ojo.

Uno de los efectos de aumento de una lente se puede obtener sin una lente de una manera muy sencilla, con un agujero de alfiler. Si miras un objeto cercano a través de un agujero de alfiler, puedes traerlo

mucho más cerca de tu ojo. La razón es que solo un haz de luz estrecho atraviesa el estenopeico desde cada punto del objeto que estás mirando, por lo que no se requiere mucho enfoque. El tamaño de la imagen en tu retina no aumenta cuando miras el objeto a través de un estenopeico a la misma distancia que sin el estenopeico, pero con el estenopeico, puedes acercarlo mucho más a tu ojo sin borrosidad, y por lo tanto haces que parezca más grande.

También puede haber jugado con cámaras estenopeicas, en las que se forma una imagen en una pantalla en una caja oscura sin lente, como se muestra en la Figura\( 11.45\).

Figura\( 11.45\):

Una desventaja de una cámara estenopeica es que necesitas un objeto muy brillante. Tiras la mayor parte de la luz que viene del objeto. Se puede obtener más luz haciendo el agujero de alfiler más grande, pero eso hace que la imagen sea más difusa. En realidad, sin embargo, no se puede hacer el agujerito demasiado pequeño de todos modos. En definitiva, como veremos en el capítulo 13, la difracción limita la resolución de una cámara estenopeica. Si intentas hacer que la imagen sea muy nítida haciendo que el estenopeico sea muy pequeño, el haz que obtengas dentro de la cámara se esparcirá por difracción. Lo mejor que puedes hacer es elegir

el tamaño de su estenopeica para que la dispersión en la pantalla debido a la difracción solo coincida con el tamaño del agujero de alfiler.

Mientras estamos en el tema, tenga en cuenta que la difracción y el tamaño finito de su pupila limitan la resolución angular de su ojo. Como entenderemos en detalle en el capítulo 13, el tamaño finito,\(s\) de tu pupila introduce una dispersión angular de orden\(d / \lambda\) para la luz de longitud de onda\(\lambda\). A menos que tengas ojos enormes,\(s\) es inferior a .25 cm, por lo que para la luz verde con longitud de onda de 500 nanómetros (550 es aproximadamente la mitad del espectro visible), la resolución angular es mayor que aproximadamente 2 × 10−4. A una distancia de 10 metros, por ejemplo, aunque tus ojos sean perfectos, no podrás resolver dos objetos a menos de unos pocos milímetros de distancia.

Puedes usar un agujero de alfiler para estudiar tus ojos de maneras bastante interesantes. Pon el agujero cerca de tu ojo y mira una fuente de luz difusa brillante. Haremos esto en conferencia, pero puedes hacer tu propio estenopeico perforando un pequeño agujero en una pieza de papel de aluminio con un alfiler y probarlo. Si usas anteojos, quítalos. No los vas a necesitar. Deberías ver un punto de luz circular. Esta es la imagen de tu pupila en tu retina, como se muestra a continuación:

Figura\( 11.46\):

Puedes ver el cambio de tamaño de tu pupila con este arreglo. Sólo tienes que cubrirte o cerrar el otro ojo. Debido a que ahora estás recibiendo menos luz, ambas pupilas se expandirán. Destapa el otro ojo y vuelve a mirar la luz brillante y las pupilas se contraen. ¿Se puede notar un breve lapso de tiempo?

Ahora trae con cuidado una punta de pluma o lápiz desde abajo entre el agujero de alfiler y tu ojo, hasta que apenas empiece a oscurecer tu vista. ¿Qué ves? Esto debería convencerte, si no estabas seguro antes, de que la imagen en tu retina está al revés, como se muestra en la Figura\( 11.47\). Falta la mitad inferior de la imagen en tu retina. Tu cerebro, siendo usado

Figura\( 11.47\):

a ver imágenes en la retina boca abajo, ¡interpreta esto como un objeto que baja desde arriba!

Ampliación, telescopios, microscopios y todo eso

Al combinar lentes de varias maneras, puede construir todo tipo de instrumentos ópticos interesantes. La forma más sencilla de pensar sobre el aumento es simplemente considerar el tamaño angular de la imagen observada, en comparación con el tamaño angular que verías sin el instrumento.

Un simple telescopio se ilustra en la Figura\( 11.48\). Las distancias son algo distorsionadas. En un telescopio real el objeto estaría mucho más lejos y los tamaños de las lentes mucho más pequeños. Cuando miras un objeto distante (grande\(L\)) con tu telescopio, la luz llega a la primera lente (“objetivo”) como un haz de rayos casi paralelo. Sabemos por la fórmula de lente delgada\[\frac{1}{d_{1}}+\frac{1}{d_{2}}=\frac{1}{f}\]

con\(d_{1}=L \gg f\) eso se forma una imagen real a una distancia del objetivo\(d_{2}\) ligeramente mayor que su distancia focal\(f_{1}\). Luego, el “ocular” se coloca a una distancia justo más allá de su distancia focal\(f_{2}\), desde la imagen real, para convertir la luz de la imagen en un haz casi paralelo

Figura\( 11.48\):

otra vez. Esencialmente lo que estás haciendo con el ocular es mirar la luz de la imagen real con una lupa.

Podemos entender cómo (y cuánto) un telescopio magnifica objetos distantes mirando los ángulos involucrados. Si el objeto tiene tamaño\(h_{o}\), su tamaño angular sin el telescopio es\[\frac{h_{o}}{L+f_{1}+f_{2}} \approx \frac{h_{o}}{L}\]

Por triángulos similares, el tamaño de la imagen real es\[\frac{h_{o}}{L} \cdot f_{1}\]

y así el tamaño angular de la imagen real en el ocular (y su ojo) es\[\frac{h_{o}}{L} \cdot \frac{f_{1}}{f_{2}}\]

Por lo tanto, el aumento es aproximadamente\[\frac{f_{1}}{f_{2}}\]

Tenga en cuenta que la imagen del telescopio aparece al revés porque lo que en realidad está viendo es la imagen real.

Un microscopio se parece a lo que se muestra en la Figura\( 11.49\) (con aún menos rayos de luz dibujados porque deberías estar acostumbrándote a ellos para este momento.

Figura\( 11.49\):

La muestra se coloca apenas un poco más que la distancia focal,\(f_{1}\), lejos del objetivo para que se forme una imagen real que sea mucho más grande que la muestra. Entonces miras la imagen real con el ocular como lupa, nuevamente posicionada un poco más que su distancia focal,\(f_{2}\), lejos, para poder visualizar la imagen cómodamente con los ojos relajados. Si la muestra tiene tamaño\(h_{o}\), el tamaño de la imagen real es\[\frac{L}{f_{1}} \cdot h_{o}\]

y el tamaño angular de la imagen en el ocular (y su ojo) es\[\frac{L h_{o}}{f_{1} f_{2}}\]

Esto debe compararse con el tamaño angular del objeto en alguna longitud de referencia\(L_{0} \approx 25 \mathrm{~cm}\), en la que se puede ver el objeto cómodamente a simple vista, que es\[\frac{h_{o}}{L_{0}}\]

Así, el aumento es\[\frac{L L_{0}}{f_{1} f_{2}}\]