11.7: Arco iris

La mayoría de los libros de física elemental o no explican el arco iris en absoluto, o lo explican incorrectamente (a veces vergonzosamente). Obviamente, tiene algo que ver con la refracción de la luz por las gotas de lluvia. Deberíamos poder explicarlo solo usando la ley de Snell y la óptica geométrica: el trazado de rayos. Pero es un poco sutil, como verás.

Para empezar, considere la refracción de un estrecho rayo de luz de una gota esférica de agua, ilustrada en la Figura\( 11.50\). El índice de refracción del agua,\(n\), varía de aproximadamente 1.332 para la luz roja a aproximadamente 1.343 para la luz violeta. El rayo entra en algún lugar de la gota, que puede parametrizar por el ángulo\(\theta\) entre la dirección de la luz entrante y el radio desde el centro de la gota hasta el punto donde entra la luz. El ángulo\(\theta\) es también el ángulo entre el rayo de luz y la perpendicular a la superficie de la gota, por lo que es lo apropiado usar en la ley de Snell. Así, el ángulo\(\phi\) del rayo refractado dentro de la gota viene dado por\[\sin \phi=\frac{1}{n} \sin \theta\]

o\[\phi=\sin ^{-1}\left(\frac{\sin \theta}{n}\right)\]

Figura\( 11.50\):

Parte de la luz también se refleja desde la gota. Obsérvese que la luz reflejada se refleja especularmente. Porque\(\theta = 0\), la luz se refleja directamente hacia atrás. A\(\theta\) medida que aumenta desde 0 el rayo reflejado se gira en sentido antihorario con respecto al rayo entrante en un ángulo\(\pi-2 \theta\) hasta que en\(\theta=\pi / 2\) él solo besa la esfera y no se gira en absoluto.

El dato geométrico importante que hace que el problema sea bastante simple es que el ángulo entre el rayo y la perpendicular a la superficie es el mismo cuando sale de la gota que cuando entra. La ley de Snell funciona a la inversa, y el rayo que sale de la gota forma un ángulo\(\theta\) con la perpendicular. Como se puede ver en la Figura\( 11.51\), esto significa

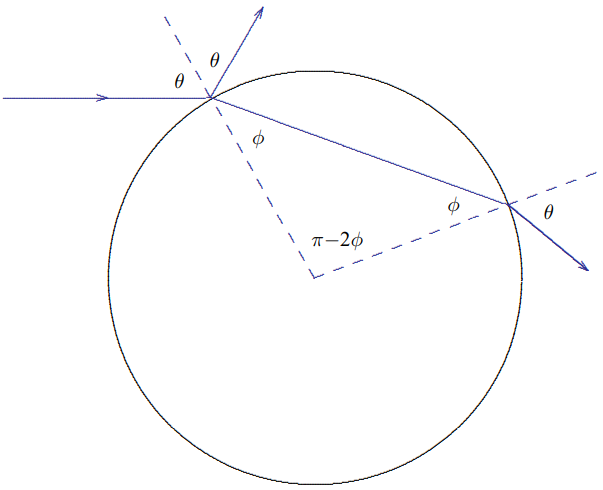
Figura\( 11.51\):

que el rayo refractado que sale de la gota Esto es solo una versión del rayo reflejado en Figura\( 11.50\) girado por\(\pi-2 \phi\). Esto significa que es girado por\[\theta_{1}=(\pi-2 \phi)-(\pi-2 \theta)=2 \theta-2 \phi\]

desde la dirección original de la luz entrante.

El problema con esto es que no tiene nada que ver con el arco iris. El problema es que la dirección del rayo refractado es básicamente hacia adelante y depende de ello\(\theta\), de manera que no\(\theta\) se escoge ningún valor particular de. Hay tres cosas misteriosas sobre el arco iris que este efecto no puede explicar.

1. El arco iris primario ocurre en un ángulo definido, y
2. el ángulo está en la dirección hacia atrás, en un ángulo de aproximadamente\(41^{\circ}\) (aproximadamente .7 radianes) desde el rayo de luz entrante, que gira aproximadamente 2.4 radianes desde la dirección original, y
3. hay un segundo arco iris fuera del primero en el que los colores van en sentido contrario!

Figura\( 11.52\): Gráfica de\(\theta_{1}\) versus\(\theta\) para luz roja y luz azul.

Entonces, ¿qué hace esta refracción? ¡La respuesta es casi nada! El rayo refractado se extiende sobre un amplio rango de ángulos, como se muestra en la gráfica de la Figura\( 11.52\). En cualquier ángulo saliente particular, la luz de este efecto es muy tenue y apenas perceptible. No sólo los colores no están muy separados, sino que todos ellos están repartidos de manera más o menos uniforme sobre el ángulo saliente, por lo que no se ve ningún arcoíris de esta refracción.

Entonces, ¿de dónde viene el arco iris? La respuesta es que además de ser refractado desde la superficie interior de la gota, el rayo también puede reflejarse, para luego salir en un ángulo aún mayor. El resultado se parece a la imagen de la Figura\( 11.53\).

Comparando Figura\( 11.51\), Figura\( 11.53\) y Ecuación (11.165), es claro que para esta trayectoria la luz es girada por\[\theta_{2}=2(\pi-2 \phi)-(\pi-2 \theta)=2 \theta+\pi-4 \phi\]

Y ahora aquí está el punto crítico. Si trazamos este\(\theta_{2}\) versus\(\theta\), ¡la gráfica tiene un mínimo! Esto se muestra en la Figura\( 11.54\).

Ahora el ángulo de salida tiene un mínimo para\(\theta \approx 1.05\) (que es el valor de\(\theta\) ilustrado en los diagramas). El ángulo saliente\(\theta_{2} \equiv \theta_{\text {out }}\) correspondiente a éste\(\theta\) da la posición angular del arco iris. Aquí, porque\(\theta_{2}\) no cambia mucho por un pequeño cambio en\(\theta\), se ve la suma de la luz refractada desde un rango de\(\theta\) s alrededor del mínimo. El ángulo es sobre lo que esperamos,\(\theta_{\text {out }} \approx \pi-.7\), donde\(.7 \text { radians } \approx 41^{\circ}\) está el ángulo entre un vector de la gota de agua al sol y la misma gota a tu ojo, como se muestra en la Figura\( 11.55\). El signo negativo de entrada\(\pi-.7\) significa que la luz no ha girado por completo\(180^{\circ}\), por lo que la luz que llega a tu ojo entró en la gota de agua refractante en el lado más alejado de ti.

Figura\( 11.53\):

También se puede ver en la gráfica en Figura\( 11.54\) que los colores están dispersos. La luz roja está en el exterior (más lejos de\(2 \pi\)) y la luz azul en el interior.

Matemáticamente, ¿por qué la luz se amontona en el borde? La energía de la luz solar que cae sobre una pequeña parte de la superficie del agua cae entre\(\theta\) y\(\theta+d \theta\) es proporcional a\(I d \theta\) (hay otros factores, como\(\cos \theta\), pero varían lentamente, así que olvidemos ellos). El ángulo del rayo saliente,\(\theta_{out}\) es una función de\(\theta\), y la energía\(\propto I_{i} d \theta\) se extiende sobre una región angular entre\(\theta_{out}\) y\(\theta_{\text {out }}+d \theta_{\text {out }}\). Así la intensidad saliente es proporcional a\ [\ begin {aligned}
&\ text {entrante}\\
&\ text {energía entre}\ propto I_ {i} d\ theta\
&\ theta\ text {y}\ theta+d\ theta
\ end {alineado}\]

\ [\ begin {reunió}
\ text {saliente}\\\
=\ quad\ texto {energía entre}\ quad\ propto I_ {o} d\ theta_ {\ text {\ text {out}}
\\ theta_ {\ text {out}}\ text {y}\ theta_ {\ text {out}} +d\ theta_ {\ text {out}}
\ end {reunidos}\]

\[I_{o} \propto \frac{I_{i} d \theta}{d \theta_{\text {out }}}=\frac{I_{i}}{\frac{d \theta_{\text {out }}}{d \theta}}\]

Figura\( 11.54\): Gráfica de\(\theta_{2}\) versus\(\theta\) para luz roja y luz azul.

Figura\( 11.55\):

Cuando\(d \theta_{\text {out }} / d \theta=0\), ¡la intensidad va al infinito! El borde es infinitamente más brillante que el interior. ¡Por eso lo vemos!

Figura\( 11.56\):

Ahora podemos comprobar esta imagen viendo cómo explica el segundo arcoíris. Como se puede adivinar, esto viene de otra reflexión más, como se muestra en la Figura\( 11.56\).

Ahora el rayo de luz es girado por\[\theta_{3}=3(\pi-2 \phi)-(\pi-2 \theta)=2 \theta+2 \pi-6 \phi\]

Esto se muestra, junto con\(\theta_{2}\), en la gráfica de la Figura\( 11.57\). El mínimo de\(\theta_{3}\) es la posición del segundo arco iris. Pero ahora porque el ángulo es mayor que\(\pi\), la luz está llegando a tu ojo desde el lado de la gota que está más cerca de ti, y se inclina completamente alrededor.

Es por ello que los colores se invierten. Nuevamente el azul se refracta más, pero esta vez eso significa que el azul está en el exterior, mientras que el rojo adentro en el interior.

Por accidente, los mínimos para\(\theta_{2}\) y\(\theta_{3}\) están casi por igual (dentro de unos .13 radianes) desplazados\(\pi\), aunque en lados opuestos. Es por ello que los dos arcoíris están bastante juntos en el cielo.

Figura\( 11.57\): Gráfica de\(\theta_{2}\) y\(\theta_{3}\) versus\(\theta\) para luz roja y luz azul.

Otra predicción de esta imagen que a menudo se puede ver es “La banda oscura de Alexander” que aparece entre los arcoíris. La luz que no se concentra en el valor mínimo de\(\theta\) se extiende dentro del primer arco iris sino fuera del segundo arco iris, así la región entre los dos arcoíris (o fuera del primero si no se puede ver el segundo) es más oscura. Si trazamos la distancia angular de\(\pi\) distancia en función del ángulo en el que la luz solar entrante entra en la gota de agua, el primer y segundo arco iris se ven como Figura\( 11.58\) (como de costumbre, he exagerado la diferencia en el índice de refracción entre rojo y azul. Aquí se ve claramente que el ángulo del primer arco iris es más pequeño, y la banda oscura entre los dos.