13.5: Convolución

Hay un teorema bastante simple, conocido como teorema de convolución, que es extremadamente útil para tratar con las transformadas de Fourier. Supongamos que tenemos dos funciones,\(f_{1}(x)\) y\(f_{2}(x)\). Defina la función de\(f_{1} \circ f_{2}\) la siguiente manera:\[f_{1} \circ f_{2}(x)=\int_{-\infty}^{\infty} d y f_{1}(x-y) f_{2}(y)\]

Esta integral estará bien definida si\(f_{1}(x)\) y\(f_{2}(x)\) caerá lo suficientemente rápido al infinito (y ciertamente si son distintos de cero solo en una región finita de\(x\)). Tenga en cuenta que\(f_{1} \circ f_{2}\) es una función de una sola variable. También es simétrica bajo el intercambio de las dos funciones, pues por un simple cambio de variables\((y \rightarrow x-y)\)\[f_{1} \circ f_{2}(x)=\int_{-\infty}^{\infty} d y f_{1}(x-y) f_{2}(y)=\int_{-\infty}^{\infty} d y f_{1}(y) f_{2}(x-y)=f_{2} \circ f_{1}(x)\]

Ahora el teorema es que la transformada de Fourier de la convolución es\(2\pi\) veces el producto de las transformaciones de Fourier de las dos funciones. La prueba es inmediata (todas las integrales van desde −\(\infty\) hasta\(\infty\)):\ [\ begin {aligned}
C_ {f_ {1}\ circ f_ {2}} (k) =\ frac {1} {2\ pi}\ int d x e^ {i k x} f_ {1}\ circ f_ {2} (x)\\
=&\ frac {1} {2\ pi}\ int d x e^ {i k x}\ int d y f_ {1} (x-y) f_ {2} (y)
\ final {alineado}\]

Ahora sustituimos\(x \rightarrow y+z\) y escribimos la integral sobre\(y\) y\(z\),\ [\ begin {recopilados}
=\ frac {1} {2\ pi}\ int d z e^ {i k (y+z)}\ int d y f_ {1} (x-y) f_ {2} (y)\\
=\ frac {1} {2\ pi}\ int d z e^ {i k z} f_ {1} (z)\ int d y e^ {i k y} f_ {2} (y) =2\ pi C_ {f_ {1}} (k) C_ {f_ {2}} (k).
\ end {reunido}\]

El análogo bidimensional de (13.79) es una extensión directa. La convolución bidimensional es\[f_{1} \circ f_{2}(x, y)=\int d x^{\prime} d y^{\prime} f_{1}\left(x-x^{\prime}, y-y^{\prime}\right) f_{2}\left(x^{\prime}, y^{\prime}\right)\]

\[C_{f_{1} \circ f_{2}}\left(k_{x}, k_{y}\right)=4 \pi^{2} C_{f_{1}}\left(k_{x}, k_{y}\right) C_{f_{2}}\left(k_{x}, k_{y}\right)\]

Patrones repetidos

El teorema de la convolución puede ser utilizado para entender muchas situaciones interesantes. Considere el siguiente patrón muy instructivo de dos ranuras anchas:\ [f (x, y) =\ left\ {\ begin {array} {l}
1\ text {for} -a\ leq x\ leq a\\
1\ text {for} -a\ leq x-b\ leq a\\
0\ text {de lo contrario}
\ end {array}\ right.\]

para\(b > 2a\). Una pieza del patrón se muestra en la Figura\( 13.15\) para\(b = 3.5a\).

Figura\( 13.15\): Una pieza de la barrera opaca con dos ranuras anchas.

Esto puede considerarse como la convolución de dos funciones:\[f=f_{1} \circ f_{2}\]

donde\ [f_ {1} (x, y) =\ left\ {\ begin {array} {l}
1\ text {for} -a\ leq x\ leq a\\
0\ text {de lo contrario}
\ end {array}\ derecha.\]

y\[f_{2}(x, y)=\delta(x) \delta(y)+\delta(x-b) \delta(y)\]

f2 (x, y) = δ (x) δ (y) + δ (x − b) δ (y). Las correspondientes transformaciones de Fourier son, de (13.70) (13.84) (13.85) Ct1 (kx, ky) = sin (kxa) π kx δ (ky) (13.86) y de (13.73) Cf2 (kx, ky) = 1 4π2 cos bkx 2 e−ibkx/2. Ahora aplicando el teorema de convolución da (13.87) cF1◦F2 (kx, ky) = cos bkx 2 e−ibkx/2 sin (kxax) π kx δ (ky). (13.88) 13.6. PERIÓDICO f (x, y) 395 Debido a que b > 2a, esto describe un patrón que oscila rápidamente en la escala establecida por 1/b, con una amplitud que varía con el patrón de difracción de hendidura única caracterizado por el tamaño 1/a. el patrón de intensidad en una pantalla distante se muestra en la figura 13.16, para b = 3.5a La línea punteada es la patrón para una sola hendidura ancha (compare (13.5)).

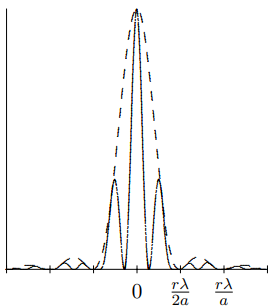
Figura\( 13.16\): El patrón de difracción para dos ranuras anchas.