13.4: Ejemplos

Sencilla

Supongamos que\ [f (x, y) =\ left\ {\ begin {array} {l}
1\ text {for} -a\ leq x\ leq a\\
0\ text {for} |x|>a
\ end {array}\ right.\]

independiente de\(y\). Esto es realmente un problema bidimensional, porque podemos guardarlo\(k_{y} = 0\) e ignorarlo (excepto por un factor de\(2\pi\), del que no nos preocuparemos) bajando la\(k_{y}\) integral de (13.19). (13.24)\[C\left(k_{x}, k_{y}\right)=\frac{1}{4 \pi^{2}} \int d x d y f(x, y) e^{-i\left(k_{x} x+k_{y} y\right)}\]

se convierte (con el\(2\pi\) corregido para hacerlo unidimensional) ⁷\ [\ begin {reunió}
C\ izquierda (k_ {x}\ derecha) =\ frac {1} {2\ pi}\ int_ {-\ infty} ^ {\ infty} d x f (x) e^ {-i k_ {x} x}\\
=\ frac {1} {2\ pi}\ int_ {} ^ {a} d x e^ {-i k_ {x} x} =\ izquierda. \ frac {1} {-2 i\ pi k_ {x}} e^ {-i k_ {x} x}\ derecha|_ {-a} ^ {a} =\ frac {\ sin k_ {x} a} {\ pi k_ {x}}.
\ end {reunido}\]

Por lo tanto, esperamos que la intensidad de la ola en general\(z\) sea proporcional a\(\left|C\left(k_{x}\right)\right|^{2}\),\[I(x, y) \propto \frac{\sin ^{2}\left(k_{x} a\right)}{k_{x}^{2}}\]

donde\[\frac{x}{r}=\frac{k_{x}}{k}=\frac{k_{x}}{\omega / v}\]

o\[k_{x}=\frac{\omega}{v} \frac{x}{r}.\]

Así, si medimos la intensidad del haz difractado, a una\(r\) distancia de la abertura, la intensidad va de la siguiente manera: ⁸\[I(x, y) \propto \frac{\sin ^{2}(2 \pi a x / r \lambda)}{x^{2}}\]

donde\(\lambda\) está la longitud de onda de la luz. Una gráfica de\(I\) como función de\(x\) se muestra en la Figura\( 13.5\). Esto se llama patrón de difracción. En el importante caso de que la luz pase a través de una pequeña abertura, el patrón de difracción se puede observar fácilmente proyectando el haz difractado sobre una pantalla. Las características de este patrón que vale la pena señalar son el gran máximo en\(x = 0\), con el doble de ancho que todos los demás máximos, y los ceros periódicos para\(x=n r \lambda / 2 a\). Obsérvese también que a medida que disminuye el ancho,\(a\) de la hendidura, aumenta el tamaño del patrón de difracción.

Moral: Esta relación inversa entre el tamaño de la hendidura y el tamaño del patrón de difracción es otra ilustración de la característica general de las transformaciones de Fourier discutidas en el Capítulo 10.

Difracción de campo cercano

Haremos una pausa aquí para discutir la región para la difracción intermedia\(z\) de Fresnel, donde el problema de la difracción es complicado. Todo lo que podemos hacer es evaluar la integral, (13.19), numéricamente, por computadora, y encontrar la intensidad aproximadamente a diversos valores de\(z\). Por ejemplo, supongamos que tomamos\[\frac{\omega}{c}=\frac{2 \pi}{\lambda}=\frac{100}{a},\]

Figura\( 13.5\): La intensidad del patrón de difracción en función de\(x\).

correspondiente a una hendidura bastante pequeña, con un ancho de solo\(100 / \pi \approx 32\) veces la longitud de onda de la onda. Luego utilizaremos (13.19) para calcular la intensidad de la onda a diversos valores de\(z\), en unidades de\(a\). Para pequeños\(z\), el resultado se muestra en la Figura\( 13.6\). Se puede ver que la forma básica de la viga se mantiene por un tiempo, como esperábamos de (13.28). Sin embargo, los meneos se desarrollan de inmediato. La difracción ondulada bastante grande se debe a los bordes afilados. A continuación, daremos otro ejemplo en el que la difracción es mucho más suave. Para intermedio\(z\), que se muestra en la Figura\( 13.7\), los meneos comienzan a fusionarse y cambian drásticamente la forma general de la viga. Al mismo tiempo, la viga comienza a extenderse.

Figura\( 13.6\): La intensidad de una ola que pasa por una hendidura, para pequeños\(z\).

Finalmente, en la Figura\( 13.8\), se muestra el acercamiento a las\(z\) regiones grandes, donde la difracción se hace cargo por completo y aparece el patrón de difracción de campo lejano, (13.54).

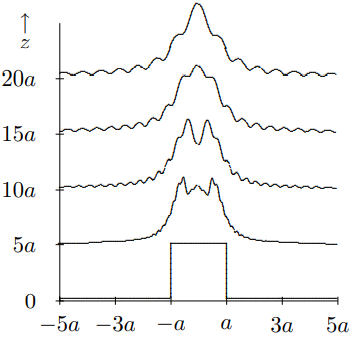
Figura\( 13.7\): La intensidad de una onda que pasa por una hendidura, para intermedio\(z\).

Figura\( 13.8\): La intensidad de una ola que pasa por una hendidura, ya que\(z\) se agranda.

Un ejemplo más puede ser interesante. Supongamos que en lugar de ser un simple agujero en la pantalla opaca, la abertura está sombreada de tal manera que la perturbación de la ola en\(z = 0\) tiene la forma\[f(x, y)=e^{-|x| / a}.\]

La transformada de Fourier aquí se realizó en el Capítulo 10 en (10.49) - (10.56). Sustituyendo\(\omega \rightarrow k_{x}\) y\(\Gamma \rightarrow 1 / a\) en (10.56) da\[C\left(k_{x}\right)=\frac{1}{\pi} \frac{a}{1+a^{2} k_{x}^{2}}.\]

Esto determina la distribución de intensidad en general\(z\). Sin embargo, a diferencia del ejemplo anterior, este patrón da una difracción muy suave. Para pequeños\(z\), el patrón de intensidad se muestra en la Figura\( 13.9\). El punto agudo en (13.56) desaparece, pero por lo demás el cambio es muy gradual porque el patrón inicial es muy suave excepto en\(x = 0\). Para intermedio y grande\(z\), los patrones de intensidad se muestran en Figura\( 13.10\) y Figura\( 13.11\).

Figura\( 13.9\): La distribución de intensidad de (13.56) para pequeños\(z\).

Figura\( 13.10\): La distribución de intensidad de (13.56) para intermedio\(z\).

Figura\( 13.11\): La distribución de intensidad de (13.56) para grandes\(z\).

Rectángulo

Supongamos\ [f (x, y) -\ left\ {\ begin {array} {l}
1\ text {for} -a_ {x}\ leq x\ leq a_ {x}\ text {y} -a_ {y}\ leq y\ leq a_ {y},\\
0\ text {de lo contrario}.
\ end {array}\ derecho.\]

Este es el producto de un solo patrón de hendidura\(x\) con un solo patrón de hendidura en\(y\). La transformada de Fourier es el producto de las transformadas unidimensionales de Fourier\ [\ begin {alineadas}
C\ left (k_ {x}, k_ {y}\ right) =&\ frac {1} {4\ pi^ {2}}\ int_ {-a_ {x}} ^ {a_ {x}} d x e^ {-i k_ {x} x}\ int_ {-a_ {-a_ {-a_ _ {y}} ^ {a_ {y}} d y e^ {-i k_ {y} y}\\
&=\ frac {\ sin\ izquierda (k_ {x} a_ {x}\ derecha)} {\ pi k_ {x}}\ frac {\ sin\ izquierda (k_ {y} a_ {y}\ derecha)} {\ pi k_ {y}}
\ final {alineado}\]

Por lo tanto, la intensidad se parece aproximadamente a\[I(x, y) \propto \frac{\sin ^{2}\left(2 \pi a_{x} x / r \lambda\right)}{x^{2}} \frac{\sin ^{2}\left(2 \pi a_{y} y / r \lambda\right)}{y^{2}}.\]

Por supuesto, una vez más, debido a las propiedades generales de la transformada de Fourier, si el rectángulo es estrecho en\(x\), el patrón de difracción se dispersa en\(k_{x}\), y de manera similar para\(y\).

\(\delta\)“Funciones”

A medida que la rendija de entrada (13.49) se estrecha, el patrón de difracción se extiende. Por supuesto, la intensidad también disminuye. La intensidad at\(k_{x} = 0\) está relacionada con la transformada de Fourier de\(f\) a cero, que es solo la integral de\(f\) sobre todo\(x\). A medida que la hendidura se estrecha, esta integral disminuye. Pero supongamos que aumentamos la intensidad del haz entrante, a medida que\(a\) disminuye, para mantener fija la intensidad del máximo del patrón de difracción. Ignorando la\(y\) dependencia, requerimos\ [f_ {a} (x) =\ left\ {\ begin {array} {l}
\ frac {1} {2 a}\ text {for} -a\ leq x\ leq a,\\
0\ text {for} |x|>a.
\ end {array}\ right.\]

El límite del\(f_{a}\) as\(a \rightarrow 0\) no existe realmente como una función. Es cero en todas partes excepto\(x = 0\). Pero va a\(\infty\) muy rápido en\(x = 0\), así que\[\lim _{a \rightarrow 0} \int d x f_{a}(x)=1\]

Es extraordinariamente conveniente inventar un objeto con estas propiedades, llamado “\(\delta\)-función”. Es decir,\(\delta(x)\) tiene la propiedad que es cero excepto en\(x = 0\), y que\[\int d x \delta(x)=1.\]

De hecho, este objeto tiene una especie de sentido matemático, siempre y cuando no lo cuadren. \(\delta\)-las funciones pueden ser manipuladas como funciones ordinarias, sumadas, multiplicadas por constantes o funciones suavizadas —\(\delta\) -las funciones de diferentes variables pueden incluso multiplicarse — ¡simplemente no las cuadren! Por ejemplo, una función delta se puede multiplicar por una función continua ordinaria:\[f(x) \delta(x)=f(0) \delta(x)\]

donde sigue la igualdad porque la función delta desaparece excepto at\(x = 0\), de manera que sólo importa el valor de\(f\) at 0.

Ahora bien, debería quedar claro a partir de (13.63) y (13.64) que la transformada de Fourier de\(\delta(x)\) es solo una constante:\[C(k)=\frac{1}{2 \pi} \int d x e^{-i k x} \delta(x)=\frac{1}{2 \pi}.\]

El patrón de difracción para esta cosa es así muy aburrido. Hay iluminación uniforme en todos los ángulos.

Por supuesto, en física, no podemos hacer\(\delta\) -funciones. Sin embargo\(a\), si, in (13.61) es mucho menor que la longitud de onda de la onda, entonces bien podría ser una\(\delta\) función, porque solo importa para qué\(C(k_{x})\) sirve\(k_{x}<k=2 \pi / \lambda\). \(k_{x}\)Las más grandes corresponden a ondas exponenciales que mueren rápidamente con\(z\). Pero para tal\(k_{x}\), el producto\(k_{x}a\) es muy pequeño, así\[C\left(k_{x}\right)=\frac{1}{2 \pi} \frac{\sin k_{\underline{x}} a}{k_{x} a} \rightarrow \frac{1}{2 \pi}\left(1-\frac{\left(k_{\underline{x}} a\right)^{2}}{6}+\cdots\right) \approx \frac{1}{2 \pi}\]

y aún así conseguimos difracción uniforme en todos los ángulos.

Moral:\(\delta\) -las funciones son simplemente una conveniencia. Cuando los físicos hablan de una\(\delta\) función, se refieren (o al menos deberían significar) una función como\(f_{a}(x)\), donde\(a\) es menor que cualquier distancia física que sea importante en el problema. Una vez que\(a\) se vuelve tan pequeño, a menudo es más fácil hacer un seguimiento de las matemáticas cuando vas hasta el límite no físico,\(a = 0\).

Algunas propiedades de\(\delta\) -Funciones

La transformada de Fourier de a\(\delta\) -función es un exponencial complejo:\[\text { if } f(x)=\delta(x-a) \text { then } C(k)=\frac{1}{2 \pi} e^{-i k a} \text { . }\]

La transformada de Fourier de un exponencial complejo es una\(\delta\) -función:\[\text { if } f(x)=e^{-i \ell x} \text { then } C(k)=\delta(k-\ell).\]

Una\(\delta\) función -se puede alcanzar como límite en una variedad de formas diferentes. Por ejemplo, a partir de (13.68), esperaríamos que como\(a \rightarrow \infty\), la transformada de Fourier de (13.49) se acerque a una\(\delta\) función -:\[\lim _{a \rightarrow \infty} \frac{\sin k_{x} a}{k_{x}}=\delta\left(k_{x}\right) \text { . }\]

Dimensión a partir de dos

Usando\(\delta\) -funciones, podemos decir con más elegancia lo que se entiende por la afirmación que hicimos anteriormente de que si\(f(x, y)\) no depende\(y\), el problema es unidimensional. Si nos fijamos en el límite de (13.58) como\(a_{y} \rightarrow \infty\), pasa a (13.49). En otras palabras, cuando un rectángulo es infinitamente largo, es una hendidura. En este límite, la transformada de Fourier, (13.59) entra en\[\frac{\sin \left(k_{x} a_{x}\right)}{\pi k_{x}} \delta\left(k_{y}\right).\]

Este es el verdadero significado de (13.50). Es unidimensional en el sentido de que\(k_{y}\) está atascado en 0. No hay difracción en la\(y\) dirección.

Muchas rendijas estrechas

Una aplicación interesante de las funciones δ-es al patrón de difracción para varias ranuras estrechas. Utilizaremos esto más adelante de diversas maneras. Considerar una función,\(f(x, y)\) de la forma\[\sum_{j=0}^{n-1} \delta(x-j b)\]

Figura\( 13.12\): Si\(b k_{x} / k=n \lambda\), la interferencia es constructiva.

Figura\( 13.13\): El patrón de difracción para tres ranuras estrechas.

Esto describe una serie de ranuras\(n\) estrechas ⁹ en\(x = 0\)\(x = b\),\(x = 2b\),, etc., hasta\(x = (n − 1)b\). La transformada de Fourier de (13.71) es una suma de contribuciones de las\(\delta\) funciones individuales,

Figura\( 13.14\): El patrón de difracción para 6 ranuras estrechas.

de (13.67) y (13.68)\[C\left(k_{x}, k_{y}\right)=\delta\left(k_{y}\right) \frac{\perp}{2 \pi} \sum_{j=0}^{n-1} e^{-i j b k_{x}}.\]

Pero la suma es una serie geométrica que se puede hacer explícitamente:\ [\ begin {reunió}
\ sum_ {j=0} ^ {n-1} e^ {-i j b k_ {x}} =\ frac {1-e^ {-i n b k_ {x}}} {1-e^ {-i b k_ {x}}}\\
=\ frac {e^ {-i n b k_ {x}/2}\ izquierda (e^ {i n b k_ {x}/2} -e^ {-i n b k_ {x}/2}\ derecha)} {e^ {-i b k_ {x}/2}\ izquierda (e^ {i b k_ {x}/ 2} -e^ {-i b k_ {x}/2}\ derecha)} =e^ {-i (n-1) b k_ {x}/2}\ frac {\ sin n b k_ {x}/2} {\ sin b k_ {x}/2}.
\ end {reunido}\]

Así, la intensidad del patrón de difracción es proporcional a\[\frac{\sin ^{2} n b k_{x} / 2}{\sin ^{2} b k_{x} / 2}.\]

Por\(n = 2\), (13.74) es sólo\[4 \cos ^{2} \frac{b k_{x}}{2}=2\left(1+\cos b k_{x}\right).\]

Este es el problema con el que iniciamos el capítulo. Cuando\(b k_{x}=2 m \pi\) para entero\(m\), entonces la onda de una hendidura viaja más lejos que la onda de la otra por\(m \lambda\), donde\(\lambda=2 \pi / k\) está la longitud de onda. Así pues, para\(b k_{x}=2 m \pi\) la interferencia es constructiva, como se ilustra en la figura 13.12.

Para mayores\(n\), todavía obtenemos interferencia constructiva para\(b k_{x}=2 m \pi\), pero los máximos son más agudos, porque con más rendijas, hay más posibilidades de interferencia destructiva en otros ángulos. En Figura\( 13.13\) y Figura\( 13.14\), trazamos (13.74) versus\(bk_{x}\) from (−\(\pi\) to para que\(3\pi\) pueda ver dos periodos completos) para\(n = 3\) y\(6\). Observe la aparición de máximos\(n − 2\) secundarios entre los máximos primarios de la intensidad. Volveremos a estas relaciones cuando discutamos las rejillas de difracción.

____________________________________

⁶ Nuevamente, esto es simplista, ignorando las complicaciones de los límites de la misma manera que (13.15).
⁷ Tenga en cuenta que\(\sin k a / k\) está bien definido (\(= a\)) en\(k = 0\).
⁸ Aquí estamos asumiendo pequeños ángulos, así que eso\(\sin \theta \approx \tan \theta\). En nuestra discusión de las rejillas de difracción a continuación, veremos qué sucede cuando la diferencia es importante.
⁹ “Estrecho” aquí significa estrecho en comparación con la longitud de onda de la luz — ver la moral anterior.