3.9: Engrosamiento de una curva

Objetivos de aprendizaje

• Interpretar la aceleración geométricamente

Una interpretación geométrica de la aceleración

Hemos interpretado el vector de aceleración como una medida de la curvatura de una línea mundial, pero para hacer esto más que una herramienta de visualización, tendríamos que definir a qué nos referimos con curvatura. Una buena manera de abordar esto se muestra en la figura\(\PageIndex{1}\) (1).

Figura\(\PageIndex{1}\): Engrosamientos unilaterales de un círculo y un segmento de línea.

Aquí se\(L\) ha expandido un círculo de circunferencia, como una hogaza de pan levantado, a un círculo de mayor circunferencia\(L∗\). Este incremento sólo se debe a que el círculo es curvo. Si hacemos lo mismo con un segmento de línea, figura\(\PageIndex{1}\) (2), no hay incremento de longitud. El incremento en la longitud nos habla de la curvatura.

Cuantitativamente, supongamos que el grosor del área sombreada es\(∆h\). Entonces el aumento de circunferencia\(∆L = L∗ - L\) viene dado por

\[\frac{1}{L}\frac{\Delta L}{\Delta h} = k\]

donde\(k\) es una medida de curvatura, y\(k = 1/r\) para un círculo. Podemos tomar esto como una definición de la curvatura de una curva incrustada en un plano euclidiano bidimensional. Las curvas de la figura\(\PageIndex{1}\) (1) tienen ambas curvatura constante, y si hubiéramos aplicado nuestra definición a algún segmento corto de ellas, habríamos obtenido la misma respuesta. Para una curva con curvatura variable, como una letra “\(S\),” la curvatura se puede definir como el límite apropiado en cualquier punto dado, ya que la longitud del segmento que encierra el punto se acerca a cero. Tenga en cuenta que tuvimos que elegir una orientación para la expansión, es decir, una dirección en la que expandirnos. Dada esta orientación, tiene sentido hablar de valores firmados de\(h\) y\(k\). Si elegimos la orientación exterior para un círculo, entonces\(k\) es positiva.

Un punto interesante sobre esta definición es que es extrínseca más que intrínseca, en el sentido definido en la sección 2.2. Es decir, depende de cómo se incruste la curva en el espacio bidimensional ambiental, y depende de la métrica euclidiana de ese espacio. Debido a que una curva es un objeto unidimensional, no hay nada interno a la curva que nos permita definir su curvatura. Imagínate a ti mismo como un pequeño bicho, tan pequeño que eres puntiagudo. Si la curva representa tu universo, entonces puedes explorarlo tanto como quieras, pero nunca podrás detectar ninguna evidencia interna de su curvatura. Este no es el caso en dos dimensiones. Por ejemplo, un insecto que vive en la superficie bidimensional de una esfera puede detectar su curvatura dibujando triángulos y midiendo en qué medida la suma de sus ángulos interiores difiere de los\(180\) grados. Esto sería una medida intrínseca de curvatura.

La definición dada anteriormente se extiende fácilmente del espacio euclidiano a\(1 + 1\) las dimensiones del espacio-tiempo. La figura\(\PageIndex{2}\) muestra un engrosamiento unilateral de una línea mundial acelerada.

Figura\(\PageIndex{2}\): Engrosamiento unilateral de una línea mundial.

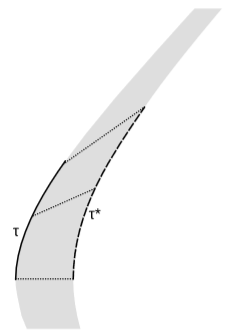
Aunque el área sombreada no se ve uniformemente gruesa a nuestros ojos euclidianos, lo es. Por ejemplo, cada una de las líneas punteadas es ortogonal a la línea mundial original de la izquierda, y todas tienen la misma longitud\(∆h\) medida por un observador que traza esa línea mundial. Es decir, cada una de estas líneas podría representar una varilla rígida de medición llevada por ese observador, trazada a lo largo de una línea que ese observador considera una línea de simultaneidad en ese momento. En analogía con el caso euclídeo, tenemos

\[\frac{1}{\tau }\frac{\Delta \tau }{\Delta h} = \frac{1}{a}\]

La paradoja de la nave espacial de Bell

Una variación de la situación mostrada en la figura\(\PageIndex{2}\) conduce a una paradoja con implicaciones filosóficas propuesta por John Bell. Bell dio la vuelta a la cafetería del CERN proponiendo el siguiente experimento pensativo a los físicos almorzando, y encontró que casi todos ellos se equivocaron.

Figura\(\PageIndex{3}\): La paradoja de la nave espacial de Bell.

Deja que dos naves espaciales aceleren como se muestra en la figura\(\PageIndex{3}\). Cada barco está equipado con un brazo de yarda, y se ata un hilo entre los dos brazos, figura\(\PageIndex{3}\) (1). El observador no acelerado\(o\) utiliza las coordenadas de Minkowski\((t,x)\), como se muestra en la figura\(\PageIndex{3}\) (2). Las aceleraciones, a juzgar por\(o\), son iguales para las dos naves como funciones de\(t\). ¿Se rompe el hilo, debido a la contracción de Lorentz?

Una diferencia crucial entre las figuras\(\PageIndex{2}\) y\(\PageIndex{3}\) (2) es que en la primera, el engrosamiento de la línea mundial se ha llevado a cabo a lo largo de las normales punteadas, mientras que la segunda línea mundial es simplemente una copia de la primera que se ha desplazado hacia la derecha, paralela al\(x\) eje.

La respuesta popular en la cafetería del CERN fue que el hilo no se rompería, siendo el razonamiento que la contracción de Lorentz es un efecto dependiente del marco, y no se observaría tal contracción en los marcos de los cohetes.

El error en este razonamiento es que las aceleraciones de las dos naves se especificaron para ser iguales en marco\(o\), no en los marcos de los cohetes. Las coordenadas de Minkowski que\((t',x')\) se muestran en la figura\(\PageIndex{3}\) (2) corresponden al marco de un observador inercial\(o'\) que se mueve momentáneamente junto con el cohete de arrastre después de que la aceleración haya estado ocurriendo por un tiempo. El\(x'\) eje es una línea de simultaneidad para\(o'\), y este eje cruza la línea mundial de la nave líder en un punto que\(o\) considera posterior en el tiempo. Por lo tanto\(o'\) dice que el buque líder ha alcanzado una velocidad mayor que la de arrastre. En\(o'\), las aceleraciones de las dos naves son desiguales.

También podemos ver directamente del diagrama de espacio-tiempo que mientras que la longitud\(L_1\) es\(4\) unidades medidas por un observador inicialmente en reposo con relación al hilo,\(L_2\) se trata de\(5\) unidades medidas por\(o'\), quien está en reposo relativo al extremo final del hilo en un momento posterior . Dado que\(L_2\) es mayor que la longitud\(L_1\) átonas, el hilo está bajo tensión.

La figura\(\PageIndex{3}\) (3) está más en el espíritu del análisis de Bell. En marco\(o\), el hilo tiene longitud inicial, sin tensión\(L\). Si el hilo hubiera estado unido únicamente al buque líder, entonces habría arrastrado detrás de él, átono, con eslora contratada por Lorentz\(L/γ\). Dado que su longitud real según o sigue siendo\(L\), se ha estirado en relación con su longitud átonas.

Esta paradoja se relaciona con la difícil cuestión filosófica de si la dilatación del tiempo y las contracciones de longitud predichas por la relatividad son “reales”. Esto depende, por supuesto, de lo que se quiere decir con “real”. Son dependientes del marco, es decir, los observadores en diferentes marcos de referencia no están de acuerdo sobre ellos. Pero esto no nos dice mucho sobre su realidad, ya que las velocidades dependen del cuadro en la mecánica newtoniana, pero a nadie le preocupa si las velocidades son reales. Bell tomó las respuestas equivocadas de sus compañeros como evidencia de que sus intuiciones habían sido equivocadas por la forma estándar de abordar esta cuestión de la realidad de las contracciones de Lorentz.

Este tratamiento tiene una verruga en él, que es que juzgamos la distancia entre los dos barcos en un marco de referencia que se combina instantáneamente con el barco de arrastre, pero esto es ligeramente diferente de la longitud determinada en el marco del barco principal. Una forma de eliminar esta verruga es notar que la discrepancia fraccionaria\(∆L_1/L_1\) es de orden\(v^3\), que es de un orden inferior a la tensión en el hilo, que es de orden\(v^2\). Sin embargo, llevar a cabo este tipo de estimación de errores de manera rigurosa sería engorroso. Un enfoque más elegante y riguroso se da en la sección 9.5, donde utilizamos técnicas más elegantes para mostrar que el movimiento que se muestra en la figura\(\PageIndex{2}\) es el movimiento único que permite que cada porción de la cuerda se mueva sin tensión.

Esta presentación incluye ideas aportadas por los usuarios de foros de física tiny-tim y PeterDonis.

Deja vu, jamais vu

Deja vu de nuevo

Figura\(\PageIndex{4}\): Deja vu.

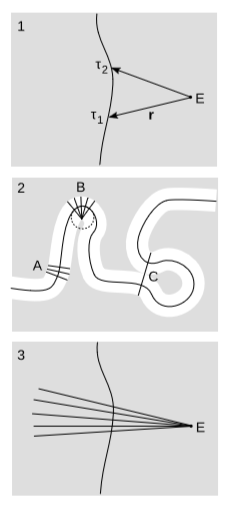
En el Ejemplo 1.4.7, vimos que cuando un observador es acelerado, puede considerar que un evento es simultáneo con ella más de una vez. Es decir, dada una línea mundial suave, similar al tiempo\(r(τ)\) parametrizada por el tiempo adecuado, y un evento\(E\), que tomamos como origen de nuestro sistema de coordenadas, puede haber más de un tiempo en el que\(r\) es ortogonal al vector de velocidad\(v\) (figura\(\PageIndex{4}\) (1)). Como se señaló anteriormente, esto es solo un problema con la aplicación de una convención de etiquetado arbitrario particular a un cierto ejemplo, no una crisis estremecedora en la física. Sin embargo, es de cierto interés geométrico intrínseco caracterizar las circunstancias bajo las cuales puede ocurrir. Nos gustaría colocar algún tipo de límite sobre cuánta aceleración se necesita y cuán distante debe estar E.

Como calentamiento, consideremos el problema análogo en el espacio euclidiano, figura\(\PageIndex{4}\) (2). Aquí tenemos la noción de barrio tubular, que es el mayor engrosamiento de una curva\(W\) tal que ningún punto en ella se encuentra en dos normales diferentes. La vecindad tubular tiene un radio\(r\), que es el mayor radio posible de una pieza de cuerda que no se cruza por sí misma cuyo eje central coincide con\(W\). Normalmente, como en la región\(A\), la cuerda no se cruza sola. Hay dos razones cualitativamente diferentes por las que la cuerda podría autocruzarse. Uno es local: el radio de curvatura de\(W\) es demasiado pequeño, como en\(B\), donde\(W\) coincide con un círculo de radio\(r\). El otro es global: dos puntos que están muy separados según se miden a lo largo\(W\) podrían estar muy juntos en el espacio euclídeo ambiental, como en el punto\(C\).

Si llevamos estas ideas al espacio Minkowski, entonces el caso local, figura\(\PageIndex{4}\) (3), es fácil de analizar utilizando las técnicas que hemos desarrollado. El análogo del radio de curvatura es el inverso de la aceleración adecuada, lo que sugiere que deberíamos ser capaces de obtener un límite en el radio de la vecindad tubular en términos de la aceleración. Definir\(f(\tau ) = r\cdot v\). En un punto dado en\(W\),\(f\) es menos la coordenada de tiempo Minkowski que un observador cuya línea mundial es\(W\) asignaría, en ese instante, a\(E\). La condición para el tipo de autointersección que estamos discutiendo es que ambos\(f\) y su derivado con respecto al tiempo adecuado\(f'\) desaparezcan en el mismo momento\(W\). Diferenciando f usando la regla del producto, nos encontramos\(f' = v\cdot v + r\cdot a = 1 + r\cdot a\) (en la\(+---\) firma), así que eso\(r\cdot a = -1\).

Ahora hacemos uso del hecho de que ambos\(a\) y\(r\) son ortogonales a\(W\) — el primero como un hecho cinemático general, y el segundo porque\(f = 0\). Esto quiere decir que se encuentran en el plano perpendicular a\(W\). La geometría de este plano es euclidiana, por lo que podemos aplicar la desigualdad euclidiana\(|a \cdot r| \leq |a| |r|\), donde las barras de la izquierda denotan el valor absoluto y las de la derecha las magnitudes de los vectores. Por lo tanto, tenemos\(|a| |r| \geq 1\). Ya que\(r\) es ortogonal a\(W\), podemos interpretarlo como la distancia adecuada entre\(E\) y\(W\). La magnitud de\(a\) es la aceleración adecuada. Al convertir a unidades con\(c \neq 1\), tenemos un encuadernado exacto de la forma\(\text{(proper distance)(proper acceleration)}\geq c^2\). En las unidades ordinarias\(c\) es grande, por lo que en este sentido\(E\) debe ser distante, y la aceleración grande. Esto explica por qué nunca encontramos tal problema en la física no relativista.

Eso nunca fue ahora

Hasta el momento hemos caracterizado las circunstancias bajo las cuales la simultaneidad puede dejar de ser única. La simultaneidad también puede dejar de existir. Por ejemplo, en la misma notación, tomar\(W\) para ser el movimiento de aceleración constante descrito en el Ejemplo 3.5.1, y dejar que\(E\) sea el evento\((-1,0)\). Entonces se puede demostrar fácilmente que siempre\(f(τ)\) es positivo, por lo que un observador que\(W\) se mueve siempre considerará\(E\) estar en su pasado, nunca en su futuro. No existe tiempo para ella tal que ella considere\(E\) “ahora”. La función\(f\) llega a un máximo en alguna parte pero nunca cruza cero.

Siempre habrá algún barrio de\(W\) dentro del cual estemos protegidos contra la inexistencia de simultaneidad. Para determinar el radio de este barrio, consideramos un evento\(B\) que se encuentra en el límite del vecindario, y definimos\(f\) en términos de\(B\) más que\(E\). Entonces\(f(τ) = 0\) para algunos\(τ\), pero\(f\) no cruza por encima de cero, para que ya sea\(f \leq 0\) en todas partes o en\(f \geq 0\) todas partes. En el lugar donde\(f(τ) = 0\), también tenemos\(f'(τ) = 0\), y el resto del análisis es el mismo que antes. Por lo tanto, el radio de la vecindad tubular determinado en ese ejemplo define un radio dentro del cual la simultaneidad tiene tanto existencia como singularidad.

Figura\(\PageIndex{5}\): El punto límite\(B\) realmente es especial.

La interpretación de tal punto límite\(B\) es un poco divertida. La figura\(\PageIndex{5}\) recapitula el movimiento descrito en el Ejemplo 3.5.1. Para este movimiento, el único punto como\(B\) es el etiquetado\((0,0)\) en las coordenadas Minkowski utilizadas en esa derivación. ¿Realmente hay algo especial en este punto, o es solo un punto aleatorio que por casualidad elegimos como origen de nuestro sistema de coordenadas? Un observador que se mueve a lo largo de esto\(W\) no cree que ningún punto del espacio-tiempo accesible para ella tenga propiedades especiales. Ella siempre ha estado acelerando y siempre lo será, por lo que ningún evento que pueda observar o afectar puede distinguirse de los otros eventos que pudo haber observado o afectado de la misma manera en cualquier momento anterior o posterior. Pero podemos demostrar fácilmente que\(B\) es especial dando una descripción de la misma sin referencia a ninguna coordenadas. \(W\)Seamos el futuro causal el conjunto de todos los eventos que se encuentran en el cono de luz futuro de algún evento en\(W\), y de manera similar para\(W\) el pasado causal. Los límites de estos dos conjuntos son los horizontes\(W\) de eventos pasados y futuros, y estos horizontes coinciden en un solo evento, que es\(B\). Esto parece paradójico, pero nuestro observador no puede observar ni afectar\(B\), por lo que no hay contradicción.