7.2: Transformación de vectores

Objetivos de aprendizaje

• Explicar cómo transformar vectores

Ahora supongamos que queremos transformar un vector cuyos componentes se expresan en las\((T,X)\) coordenadas en componentes expresados en\((t,x)\).

Figura\(\PageIndex{1}\): La transformación entre las coordenadas de Minkowski\((t,x)\) y las coordenadas aceleradas\((T,X)\)

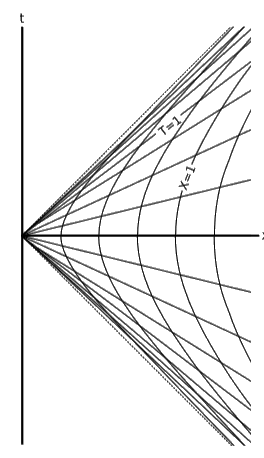
Nuestro ejemplo más básico de un vector es un desplazamiento\((∆T,∆X)\), y si hacemos de esto un infinitesimal\((dT,dX)\) entonces no necesitamos preocuparnos por el hecho de que el gráfico en figura\(\PageIndex{1}\) tiene curvas en él — de cerca, las curvas parecen líneas rectas. ¹ Si pensamos en la coordenada\(t\) como una función de dos variables,\(t = t(T,X)\), entonces\(t\) está cambiando por dos razones distintas: su primera entrada\(T\) cambia, y también su segunda entrada\(X\). Si sólo\(t\) fuera una función de una variable\(t(T)\), entonces el cambio en\(t\) estaría dado simplemente por la regla de la cadena,\(dT = \frac{dt/dT}{d} T\). Como en realidad tiene dos de esas razones para cambiar, agregamos los dos cambios:

\[dt = \frac{\partial t}{\partial T} dT + \frac{\partial t}{\partial X} dX\]

Las derivadas son derivadas parciales, y estas derivadas existen porque, como siempre asumiremos, el cambio de coordenadas es suave. Se aplica una expresión exactamente análoga para\(dx\).

\[dx = \frac{\partial x}{\partial T} dT + \frac{\partial x}{\partial X} dX\]

Antes de llevar a cabo los detalles de este cálculo, detengamos y notemos que los resultados hasta ahora son completamente generales. Dado que hasta ahora no hemos hecho uso de las ecuaciones reales para este cambio particular de coordenadas, estas expresiones se aplicarían a cualquier transformación de este tipo, incluidos los casos especiales que hemos encontrado hasta ahora, como las transformaciones de Lorentz y el escalado. (Por ejemplo, si hubiéramos escalado por un factor\(α\), entonces todas las derivadas parciales simplemente habrían igualado\(α\).). Además, nuestra definición de vector es que un vector es cualquier cosa que se transforme como un vector. Ya que hemos establecido que las reglas anteriores se aplican a un vector de desplazamiento, concluimos que también se aplicarían a cualquier otro vector, digamos un vector energía-impulso.

Volviendo a este ejemplo específico, aplicación de los hechos

\[\frac{\mathrm{d} \sinh u}{\mathrm{d} u} = \cosh u\; \; \text{and}\; \; \frac{\mathrm{d} \cosh u}{\mathrm{d} u} = \sinh u\]

nos dice que el vector\((dT,dX)\) se transforma en:

\[(dt,dx) = (X \cosh T dT + \sinh T dX ,\; X \sinh T dT + \cosh T dX)\]

Como ejemplo de cómo esto se aplica universalmente a cualquier tipo de vector, supongamos que el observador a bordo de una nave espacial con línea mundial\((T,X) = (τ,1)\) tiene un pisapapeles favorito con masa\(m\). Según mediciones realizadas a bordo de su nave, su vector energía-impulso es:

\[(p_T,p_X) = (m,0)\]

En las coordenadas no aceleradas, esto se convierte

\[\begin{align*} (p_t,p_x) &= (X \cosh T p_T + \sinh T p_X ,\; X \sinh T p_T + \cosh T p_X)\\ &= (mX\cosh T,\; mX\sinh T)\\ &= (m\cosh \tau ,\; m\sinh \tau ) \end{align*}\]

Dado que las funciones cosh y sinh se comportan como\(e^x\) para grandes\(x\), encontramos que después de que el astronauta haya pasado una cantidad razonable de tiempo adecuado\(τ\) acelerando, la energía masiva y el impulso del pisapapeles habrán crecido hasta el punto en que es un arma increíble de destrucción masiva, capaz de destruir toda una galaxia.

Referencias

¹ Aquí hacemos uso del hecho de que el cambio de coordenada fue suave, es decir, un diffeomorfismo. De lo contrario las curvas podrían tener torceduras en ellas que aún se verían como torceduras bajo cualquier ampliación.