7.3: Transformación de la Métrica

Objetivos de aprendizaje

• Explicar la transformación de la métrica cuando cambiamos de las coordenadas de Minkowski

Continuando con el ejemplo de coordenadas aceleradas, encontremos qué sucede con la métrica cuando cambiamos de coordenadas de Minkowski. Las coordenadas de Minkowski se definen esencialmente de manera que la métrica tenga la forma familiar con los coeficientes\(+1\) y\(-1\). En la relatividad, a menudo se presenta la métrica mostrando su resultado cuando se aplica a un desplazamiento infinitesimal\((dt,dx)\):

\[ds^2 = dt^2 - dx^2\]

Aquí\(ds\) representaría el tiempo adecuado, en el caso de que el desplazamiento fuera parecido al tiempo. Ya que ya hemos determinado que

\[dt = X \cosh T dT + \sinh T dX\]

y

\[dx = X \sinh T dT + \cosh T dX\]

simplemente podemos sustituir en la expresión ds para encontrar la forma de la métrica en\((T,X)\) coordenadas. Empleando la identidad\(\cosh ^2 - \sinh ^2 = 1\), encontramos

\[ds^2 = X^2 dT^2 - dX^2\]

El valor variable del\(dT^2\) coeficiente es, de hecho, exactamente el tipo de efecto gravitacional de dilatación del tiempo cuya existencia predijimos en la sección 5.2 con base en el principio de equivalencia. La forma de la métrica inferida había

\[ds^2 ≈ (1 + 2∆Φ) dT^2 - dX^2\]

donde\(∆Φ\) está la diferencia en el potencial gravitacional relativo a alguna altura de referencia. Una de las aproximaciones empleadas fue el supuesto de que el rango de alturas\(X\) era pequeño, pero sujeto a esa aproximación, los dos resultados deberían estar de acuerdo. Por conveniencia, consideremos observadores en la región\(X ≈ 1\), donde la aceleración es aproximadamente\(1\). Entonces el\(∆Φ = Φ(1 + ∆X) - Φ(1) ≈ \text{(acceleration)(height)} ≈ X\), por lo que el coeficiente de tiempo en la segunda forma de la métrica es\(≈ 1+2∆Φ ≈ 1+2∆X\). Pero a dentro del nivel de aproximación deseado, esto es lo mismo que\(X^2 = (1+∆X)^2 ≈ 1 + 2∆X\).

El procedimiento empleado anteriormente funciona en general. Para transformar la métrica de coordenadas\((t,x,y,z)\) a nuevas coordenadas\((t',x',y',z')\), obtenemos las coordenadas no cebadas en términos de las cebadas, tomamos diferenciales en ambos lados y\(t, ..., dt, ...\) eliminamos a favor de\(t', ...dt', ...\) en la expresión for\(ds^2\). Veremos en la sección 9.2, que este es un ejemplo de una ley de transformación más general para tensores, objetos matemáticos que generalizan vectores y covectores de la misma manera que las matrices generalizan vectores de fila y columna. Un escalar, sin índices, se llama tensor de rango\(0\). Los vectores y covectores, que tienen un índice, se denominan\(1\) tensores de rango.

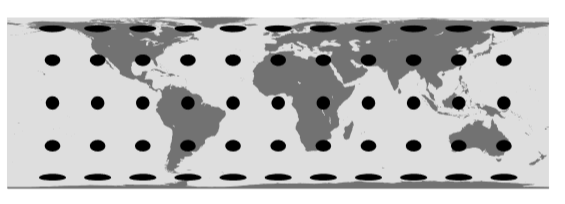
Ejemplo\(\PageIndex{1}\): A map projection

Debido a que la superficie de la tierra es curva, no es posible representarla en un mapa de flat sin distorsión. \(φ\)Sea la latitud, θ el ángulo medido hacia abajo desde el polo norte (conocido como la colatitud), ambos medidos en radianes, y dejar que a sea el radio de la tierra. Entonces, por la definición de medida radianes, un desplazamiento infinitesimal norte-sur por\(dθ\) es una distancia\(adθ\). Un punto en una cierta colatitud\(θ\) se encuentra a una\(a \sinθ\) distancia del eje, así que para una distancia infinitesimal este-oeste tenemos\(a \sin θ dφ\). Para mayor comodidad, deje que las unidades sean elegidas de tal manera que\(a = 1\). Entonces la métrica, con firma\(++\), es

\[ds^2 = dθ^2 +\sin^2 θ dφ\]

Una de las muchas formas posibles de formar un mapa flat es la proyección cilíndrica de Lambert,

\[x = φ\]

\[y = \cosθ\]

se muestra en la figura\(\PageIndex{1}\). Si vemos una distancia en el mapa y queremos saber qué tan lejos está realmente en la superficie terrestre, necesitamos

para transformar la métrica en las\((x,y)\) coordenadas. La transformación inversa de coordenadas es

\[φ = x\]

\[θ = \cos^{-1} y\]

Tomando diferenciales en ambos lados, obtenemos

\[dφ = dx\]

\[d\theta = -\dfrac{dy}{\sqrt{1-y^2}}\]

Tomamos la métrica y eliminamos\(θ\)\(φ\),\(dθ\), y\(dφ\), encontrando

\[ds^2 = (1 - y^2)dx^2 + \dfrac{1}{1 - y^2}dy^2\]

En Fgure\(\PageIndex{1}\), el patrón de lunares está hecho de figuras que en realidad son círculos, todos de igual tamaño, en la superficie terrestre. Como son bastante pequeños, podemos aproximarnos\(y\) como teniendo un solo valor para cada círculo, lo que significa que se representan en el mapa de flat como elipses aproximadas con sus dimensiones este-oeste que han sido estiradas por\((1 - y^2)^{-1/2}\) y sus dimensiones norte-sur reducidas por\((1 - y^2)^{1/2}\). Dado que estos dos factores son recíprocos el uno del otro, el área de cada elipse es la misma que el área del círculo original, y por lo tanto la misma que la de todas las otras elipses. Son una representación visual de la métrica, y demuestran la propiedad de igual área de esta proyección.

Figura\(\PageIndex{1}\): El patrón de lunares está hecho de figuras que en realidad son círculos, todos de igual tamaño, en la superficie de la tierra.