7.6: Volumen, orientación y tensor Levi-Civita

Objetivos de aprendizaje

• Introducción de alguna maquinaria geométrica que se utiliza tanto en relatividad especial como general

Esta sección opcional introduce alguna maquinaria geométrica que se utiliza tanto en relatividad especial como general.

Volumen

Propiedades deseables

En\(3 + 1\) dimensiones, tenemos una forma natural de definir el volumen de cuatro dimensiones, que es escoger un marco de referencia y dejar que el elemento de volumen esté\(dt dx dy dz\) en las coordenadas Minkowski de ese marco. Si bien esta definición de\(4\) -volumen se expresa en términos de ciertas coordenadas, resulta ser invariante de Lorentz (sección 2.5). También tiene las siguientes propiedades deseables, las cuales declaramos para un valor arbitrario de\(m\) desde\(1\) a\(4\):

1. V1. Dos\(m\) volúmenes cualesquiera pueden ser comparados en términos de su relación.
2. V2. Para cualquier vector\(m\) distinto de cero, el\(m\) -volumen del paralelepípedo que abarcan es distinto de cero si y solo si los vectores son linealmente independientes (es decir, si ninguno de ellos puede expresarse en términos de los demás usando multiplicación escalar y adición de vectores).

También nos gustaría tener métodos convenientes para trabajar con tres volúmenes, dos volúmenes (área) y un volumen (longitud). Pero los\(m\) -volúmenes para nos\(m < 4\) dan dolores de cabeza si tratamos de definirlos para que obedezcan tanto a V1 como a V2. Por ejemplo, la forma obvia de definir length (\(m = 1\)) es usar la métrica, pero entonces los vectores similares a la luz violarían V2.

Medida afín

Si estamos dispuestos a abandonar V1, entonces el siguiente enfoque tiene éxito. Considera el\(m = 1\) caso. Ignoramos completamente la métrica y aprovechamos el hecho de que en la relatividad especial, el espacio-tiempo es flat (postulado P2), de manera que el paralelismo funciona de la misma manera que en la geometría euclidiana. \(l\)Sea una línea, y supongamos que queremos definir un sistema numérico en esta línea que mida qué tan lejos están los eventos. Dependiendo del tipo de línea, esto podría ser una medida del tiempo, de la distancia espacial, o una mezcla de las dos.

Figura\(\PageIndex{1}\): Usar paralelismo para definir 1 volumen.

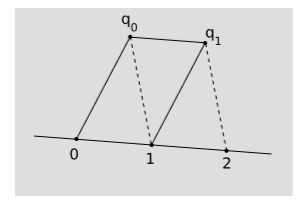
Primero seleccionamos arbitrariamente dos puntos distintos\(l\) y los etiquetamos\(0\) y\(1\), como en la figura\(\PageIndex{1}\). A continuación, escoge algún punto auxiliar\(q_0\) que no esté acostado\(l\). Construir\(q_0 q_1\) y paralelo\(01\) y\(1q_1\) paralelo a\(0q_0\), formando el paralelogramo mostrado en la figura. Continuando de esta manera, tenemos un andamiaje de paralelogramos adyacentes a la línea, determinando una celosía infinita de puntos\(1, 2, 3, ...\) en la línea, que representan los enteros positivos. Las fracciones se pueden definir de manera similar. Por ejemplo,\(\tfrac{1}{2}\) se define como el punto tal que cuando el segmento de celosía inicial\(0\tfrac{1}{2}\) se extiende por la misma construcción, el siguiente punto en la celosía es\(1\). La variable continuamente variable construida de esta manera se denomina parámetro afín. El tiempo medido por un reloj de caída libre es un ejemplo de un parámetro afín, al igual que la distancia medida por las marcas de garrapata en una regla de caída libre. Un parámetro afín solo se puede definir a lo largo de una línea recta mundial, no una curva arbitraria. La medición afín de\(1\) -volumen viola V1, porque solo nos permite comparar distancias que se encuentran sobre él\(l\) o paralelas a él. Por otro lado, tiene la ventaja sobre la medición métrica de que nos permite medir longitudes a lo largo de líneas similares a la luz.

Figura\(\PageIndex{2}\): El área de la viola se puede determinar contando los paralelogramos formados por la celosía. El área se puede determinar con cualquier precisión deseada, dividiendo los paralelogramos en partes fraccionarias que son tan pequeñas como sea necesario.

La figura\(\PageIndex{2}\) muestra cómo definir una medida afín de\(2\) -volumen, y un método similar funciona para\(3\) -volumen.

Linealidad

Figura\(\PageIndex{3}\): Linealidad del área. Duplicar el vector a duplica el área.

Supongamos que se forma un paralelogramo con los vectores a y b como dos de sus lados. Se doblamos a, luego el área se dobla también,

\[area(2a,b) = 2area(a,b)\]

En general, si escalamos cualquiera de los vectores por un factor\(c\), el área se escala por el mismo factor, siempre que fijemos alguna regla para el manejo de señales, cuestión que pospondremos hasta la sección Orientación a continuación. Algo similar sucede cuando agregamos dos vectores, e.g.

\[area(a,b + c) = area(a,b) + area(a,c)\]

de nuevo posponiendo temas con letreros. Nos referimos a estas propiedades como linealidad del\(2\) volumen afín. Cualquier medida sensible de m-volumen debe tener propiedades de linealidad similares.

Cambio de base

Figura\(\PageIndex{4}\): La viola tiene un área diferente cuando se mide usando un paralelogramo diferente como unidad.

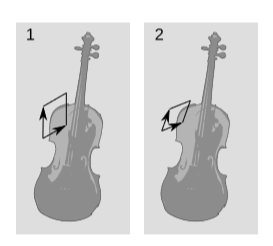
Debido a que hasta ahora no hemos hecho uso de la métrica, todas nuestras medidas de área han sido relativas y no absolutas. Como se muestra en la figura\(\PageIndex{4}\), dependen de qué paralelogramo elegimos como nuestra unidad de área. La celda unitaria en la figura\(\PageIndex{4}\) (2) es menor que la de la figura\(\PageIndex{1}\) (1), por dos razones: los vectores que definen los bordes son más cortos, y el ángulo entre ellos es menor. Palabras como “más corto” y “ángulo” nos muestran que recurrimos a la medición métrica, pero también podríamos realizar la comparación sin usar la métrica, simplemente usando paralelogramo\(1\) para medir el paralelogramo\(2\), o\(2\) para medir\(1\). Si pensamos en tal par de vectores como vectores base para el plano, entonces cambiar nuestra elección de paralelogramo unitario equivale a un cambio de base. Las áreas cambian en proporción al determinante de la matriz especificando el cambio de base.

Ejemplo\(\PageIndex{1}\): A halFLing basis

Supongamos que\(a' = a/2\), y\(b' = b/2\). El cambio de base del par no cebado al par cebado viene dado por la matriz

\[\begin{pmatrix} 2 & 0\\ 0 & 2 \end{pmatrix}\]

que tiene determinante\(4\). La reducción de ambos vectores base por un factor de\(2\) ha provocado una reducción por un factor de\(4\) en el área del paralelogramo unitario. Si usamos el paralelogramo imprimado para medir otras áreas, entonces todas las áreas saldrán más grandes por un factor de\(4\).

Las rotaciones y los potenciadores de Lorentz son cambios de base. Tienen determinantes iguales a\(1\), es decir, conservan el volumen espacio-tiempo.

Orientación

Figura\(\PageIndex{5}\): La linealidad del área requiere que a algunas áreas se les asignen valores negativos.

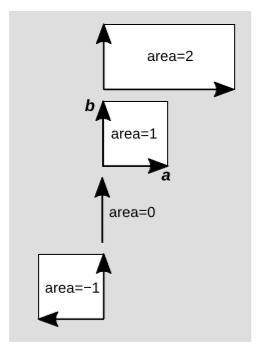
Como se muestra en la figura\(\PageIndex{5}\), la linealidad del área requiere que a algunas áreas se les asignen valores negativos. Si comparamos las áreas\(+1\) y\(-1\), vemos que la única diferencia es una de orientación, o mano. En el caso al que se le haya asignado arbitrariamente el área\(+1\), el vector b se encuentra en sentido contrario a las agujas del reloj del vector a, pero cuando a es flipped, la orientación relativa se vuelve en sentido horario.

Si has tenido los antecedentes habituales de física de primer año, entonces has visto este tema tratado de una manera particular, que es que asumimos una tercera dimensión para existir, y definimos el área para que sea el producto cruzado vectorial\(a×b\), que es perpendicular al plano habitado por\(a\) y\(b\). El problema con este enfoque es que sólo funciona en tres dimensiones. En cuatro dimensiones, supongamos que a se encuentra a lo largo del\(x\) eje -y\(b\) a lo largo del\(t\) eje -eje. Entonces, si tuviéramos que definir\(a×b\), debería ser en una dirección perpendicular a ambas, pero tenemos más de una de esas direcciones. Podríamos escoger cualquier cosa en el\(y-z\) avión.

Para comenzar con este tema en m dimensiones, donde\(m\) no necesariamente es igual\(3\), podemos considerar el\(m\) -volumen del paralelepípedo\(m\) -dimensional abarcado por\(m\) vectores. Por ejemplo, supongamos que en\(4\) -dimensional espacio-tiempo elegimos nuestros\(m\) vectores para que sean los vectores unitarios que se encuentran a lo largo de los cuatro ejes de las coordenadas de Minkowski,\(\hat{t},\hat{x},\hat{y}\; \text{and}\; \hat{z}\). De la experiencia con el producto cruzado vectorial, que es anticonmutativo, esperamos que el signo del resultado dependerá del orden de los vectores, así que tomémoslos en ese orden. Claramente sólo hay dos valores razonables que podríamos imaginar para este volumen:\(+1\) o\(-1\). La elección es arbitraria, por lo que hacemos una elección arbitraria. Digamos que es\(+1\) por esta orden. Esto equivale a elegir una orientación para el espacio-tiempo.

Una suposición oculta y no trivial fue que una vez que hicimos esta elección en un momento del espacio-tiempo, podría trasladarse a otras regiones del espacio-tiempo de manera consistente. No es necesario que este sea el caso, como se sugiere en la figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\): Una tira de Möbius no es una superficie orientable.

Sin embargo, nuestro tema en este momento es la relatividad especial, y como se discute briefly en la sección 2.4, generalmente se asume en la relatividad especial que el espacio-tiempo es topológicamente trivial, por lo que este tema surge solo en la relatividad general, y solo en el espacio-tiempo que probablemente no sean modelos realistas de nuestro universo.

Dado que\(4\) -volumen es invariante bajo rotaciones y transformaciones de Lorentz, nuestra elección de una orientación es suficiente para fijar una definición de\(4\) -volumen que es una invariante de Lorentz. Si los vectores\(a\)\(b\),\(c\),, y\(d\) abarcan un\(4\) -paralelepípedo, entonces la linealidad del volumen se expresa diciendo que hay un conjunto de coeficientes\(\epsilon _{ijkl}\) tales que

\[V = \epsilon _{ijkl} a^i b^j c^k d^l\]

Notarlo de esta manera sugiere que la interpretamos como notación abstracta de índice, en cuyo caso la falta de cualquier índice en\(V\) significa que no es solo una invariante de Lorentz sino también un escalar.

Ejemplo\(\PageIndex{2}\): HaLFLing coordinates

Deja\((t,x,y,z)\) que Minkowski coordine, y deja\((t',x',y',z') = (2t,2x,2y,2z)\). Consideremos cómo cada uno de los factores en nuestra ecuación de volumen se ve afectado a medida que hacemos este cambio de coordenadas.

\[\overset{\underbrace{V}}{\text{no change}}\; \; = \; \; \overset{\underbrace{\epsilon _{\kappa \lambda \mu \nu }}}{\times 1/16}\; \overset{\underbrace{a^{\kappa }}}{\times 2}\; \overset{\underbrace{b^{\lambda }}}{\times 2}\; \overset{\underbrace{c^{\mu }}}{\times 2}\; \overset{\underbrace{d^\nu }}{\times 2}\]

Ya que nuestra convención\(V\) es que es un escalar, no cambia bajo un cambio de coordenadas. Esto nos obliga a decir que los componentes del cambio por un factor de\(1/16\) en este ejemplo.

El resultado de Ejemplo nos\(\PageIndex{2}\) dice que bajo nuestra convención ese volumen es un escalar, los componentes de deben cambiar cuando cambiamos las coordenadas. Se podría argumentar que sería más lógico pensar en la transformación en este ejemplo como un cambio de unidades, en cuyo caso el valor de\(V\) sería diferente en las nuevas unidades; se trata de una posible convención alternativa, pero tendría la desventaja de hacer imposible la lectura del propiedades de transformación de un objeto a partir del número y posición de sus índices. Bajo nuestra convención, podemos leer las propiedades de transformación de esta manera. Aunque la sección 7.4 solo presentó estas propiedades en el caso de tensores de rango\(0\) y\(1\), aplazando la descripción general de tensores de rango superior a la sección 9.2, las propiedades\(\epsilon\) de transformación son, como lo implican sus cuatro subíndices, las de un tensor de rango \(4\). Diferentes autores utilizan diferentes convenciones respecto a la definición de\(\epsilon\), la cual fue descrita originalmente por el matemático Levi-Civita.

Figura\(\PageIndex{7}\): Tullio Levi-Civita (1873-1941) trabajó en modelos de sistemas numéricos que poseen infinitesimales y en geometría diferencial. Inventó la notación tensora, que Einstein aprendió de su libro de texto. Fue nombrado para prestigiosas cátedras dotadas en Padua y en la Universidad de Roma, pero fue despedido en 1938 por ser judío y antifascista.

Ya que por nuestra convención\(\epsilon\) es un tensor, nos referimos a él como el tensor Levi-Civita. En otras convenciones, donde no\(\epsilon\) es un tensor, se le puede denominar el símbolo Levi-Civita. Como la notación no está estandarizada, de vez en cuando pondré un recordatorio junto a ecuaciones importantes que contengan\(\epsilon\) afirmar que este es el tensorial\(\epsilon\).

El tensor Levi-Civita tiene muchos y muchos índices. ¡Da miedo! Imagina la complejidad de esta bestia. (Sob.) Tenemos cuatro opciones para el primer índice, cuatro para el segundo, y así sucesivamente, de manera que el número total de componentes es\(256\). Espera, no busques el kleenex. El siguiente ejemplo muestra que esta complejidad es ilusoria.

Ejemplo\(\PageIndex{3}\): Volume in Minkowski coordinates

Hemos configurado nuestras definiciones para que para el paralelepípedo\(\hat{t},\hat{x},\hat{y},\hat{z}\), tengamos\(V = +1\). Por lo tanto

\[\epsilon _{txyz} = +1\]

por definición, y debido a que\(4\) -volumen es Lorentz invariante, esto se mantiene para cualquier conjunto de coordenadas de Minkowski.

Si intercambiamos\(x\) y\(y\) para hacer la lista\(\hat{t},\hat{y},\hat{x},\hat{z}\), entonces como en la figura\(\PageIndex{5}\), el volumen se vuelve\(-1\), entonces

\[\epsilon _{tyxz} = -1\]

Supongamos que tomamos los bordes de nuestro paralelepípedo para ser\(\hat{t},\hat{x},\hat{x},\hat{z}\), con\(y\) omitidos y\(x\) duplicados. Estos cuatro vectores no son linealmente independientes, por lo que nuestro paralelepípedo es degenerado y tiene volumen cero.

\[\epsilon _{txxz} = 0\]

A partir de estos ejemplos, vemos que una vez que se ha fijado algún elemento de, también se pueden determinar todos los demás. La regla es que el intercambio de dos índices cualesquiera flafila el signo, y cualquier índice repetido hace que el resultado sea cero.

El ejemplo\(\PageIndex{3}\) muestra que el símbolo de fantasía\(\epsilon _{ijkl}\), que parece un jeroglífico maya secreto que invoca\(256\) diferentes números, en realidad codifica solo el valor de información de un número; cada componente del tensor es igual a este número, o menos este número, o cero. Supongamos que estamos trabajando en algún conjunto de coordenadas, que puede que no sea Minkowski, y queremos encontrar este número. Una manera complicada de encontrarlo sería usar la ley de transformación de tensores para un\(4\) tensor de rango (sección 9.2). Una forma mucho más sencilla es hacer uso del determinante de la métrica, discutido en el Ejemplo 6.2.1. Para una lista de coordenadas ijkl que se ordenan en el orden que definimos como una orientación positiva, el resultado es simplemente\(\epsilon _{ijkl} = \sqrt{\left | det\; g \right |}\). El signo de valor absoluto es necesario porque una métrica relativista tiene un determinante negativo.

Ejemplo\(\PageIndex{4}\): Cartesian coordinates and their halFLIng versions

Considera las coordenadas euclidianas en el plano, para que la métrica sea una\(2×2\) matriz, y\(\epsilon _{ij}\) tenga sólo dos índices. En las coordenadas cartesianas estándar, la métrica es\(g = diag(1,1)\), que tiene\(det\; g = 1\). Por lo tanto, el tensor Levi-Civita tiene\(\epsilon _{xy} = +1\]), and its other three components are uniquely determined from this one by the rules discussed in Example \(\PageIndex{3}\). (Podríamos haber volado todas las señales si hubiéramos querido elegir la orientación opuesta para el avión). En forma de matriz, estas reglas dan como resultado

\[\epsilon = \begin{pmatrix} 0 & 1\\ -1 & 0 \end{pmatrix}\]

Ahora transfórmate a coordenadas\((x',y') = (2x,2y)\). En estas coordenadas, la métrica es\(g' = diag(1/4,1/4)\), con\(det\; g = 1/16\), de modo que\(\epsilon _{x'y'} = 1/4\), o en forma de matriz,

\[\epsilon '= \begin{pmatrix} 0 & 1/4\\ -1/4 & 0 \end{pmatrix}\]

Ejemplo\(\PageIndex{5}\): Polar coordinates

En coordenadas polares\((r,θ)\), la métrica es\(g = diag(1,r^2)\), que tiene determinante\(r^2\). El tensor Levi-Civita es

\[\epsilon = \begin{pmatrix} 0 & r\\ -r & 0 \end{pmatrix}\]

(tomando la misma orientación que en Ejemplo\(\PageIndex{4}\)).

Ejemplo\(\PageIndex{6}\): Area of a circle

Encontremos el área del círculo unitario. Su área (firmada) es

\[A = \int \text{2-volume}(dr, d\theta )\]

donde\(dθ\) se elige el orden de\(dr\) y para que, con la orientación que hemos estado usando para el plano, el resultado salga positivo. Usando la definición del tensor Levi-Civita, tenemos

\[\begin{align*} A &= \int \epsilon _{r\theta } dx^r dx^\theta \\ &= \int_{r = 0}^{1}\int_{\theta =0}^{2\pi }rdrd\theta \\ &= \pi \end{align*}\]

El covector de 3 volúmenes

Considerar el volumen de un subespacio tridimensional de espacio-tiempo de cuatro dimensiones. La linealidad conduce a una caracterización especialmente simple del\(3\) volumen. Deje que un\(3\) -volumen sea definido por el paralelepípedo abarcado por vectores\(a\),\(b\), y\(c\). Si lanzáramos un cuarto vector\(d\), tendríamos un\(4\) -volume, y\(4\) -volume es un escalar. Este\(4\) -volumen dependería de manera lineal de los cuatro vectores, y en particular dependería linealmente de\(d\). Pero esto significa que tenemos un escalar que es una función lineal de un vector, y tal función es exactamente lo que queremos decir con un covector. Por lo tanto, podemos definir un covector de volumen de\(S\) acuerdo con

\[S_l d^l = \text{4-volume(a,b,c,d)}\]

o

\[S_l = \epsilon _{ijkl} a^i b^j c^k \; \; \; \; [\text{tensorial }\epsilon ]\]

Figura\(\PageIndex{8}\): Interpretación del covector de 3 volúmenes.

El covector de volumen recoge la información sobre el volumen del\(3\) paralelepípedo, encapsulándolo en una forma conveniente con propiedades de transformación conocidas. En particular, la afirmación y prueba del teorema de Gauss en\(3 + 1\) dimensiones se simplifican enormemente con el uso de esta herramienta. El covector\(3\) -volumen, a diferencia del\(3\) volumen afín, se define en un sentido absoluto más que en relación con algunos paralelepípedos elegidos arbitrariamente como patrón. Tanto el covector como el volumen afín no logran satisfacer la propiedad de comparación de proporciones V1, ya que no podemos comparar volúmenes a menos que se encuentren en\(3\) planos paralelos.

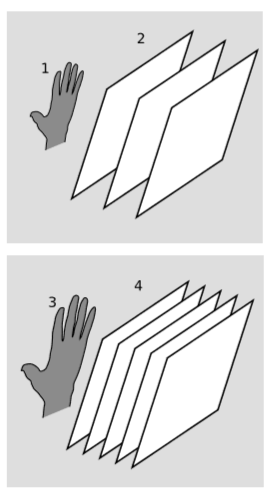
Hemos estado visualizando covectores en\(n\) dimensiones como pilas de planos\((n-1)\) -dimensionales (figura 6.3.1; figura 6.6.1). Por lo tanto, el trivector de volumen debe visualizarse como una pila\(3\) de planos en un espacio de cuatro dimensiones. Dado que la mayoría de nosotros no podemos visualizar muy bien las cosas en cuatro dimensiones, la figura\(\PageIndex{8}\) omite una de las dimensiones, de manera que las\(3\) -superficies aparecen como planos bidimensionales. La figura de mano pequeña \(\PageIndex{1}\)(1) tiene un cierto\(3\) -volumen, y el covector que lo mide está representado por la pila de\(3\) -planos paralelos a ella, figura \(\PageIndex{1}\)(2). La figura de mano más grande \(\PageIndex{1}\)(3) tiene el doble\(3\) de volumen, y su covector está representado por una pila de planos con la mitad del espaciado.

Si bajamos de cuatro dimensiones a tres, entonces el covector de volumen formado por vectores\(u\) y\(v\) se convierte en el producto cruzado vectorial\(S = u×v\), es decir,\(S_k = \epsilon _{ijk} u^i v^j\).

Ejemplo\(\PageIndex{7}\): A vector cross product

Considera el espacio euclidiano 3 en coordenadas cartesianas. Sabemos por la física de primer año que

\[\hat{z} = \hat{x}\times \hat{y}\]

Reexpresando esto en la notación anterior, tenemos\(u^x = 1\),\(v^y = 1\), y cero para todos los demás componentes de\(u\) y\(v\). Dado que el tensor Levi-Civita desaparece si tenemos algún índice duplicado, su único componente que no desaparece que puede ser relevante aquí es\(\epsilon _{xyz}= 1\). (Aquí asumimos la orientación estándar diestra para las coordenadas cartesianas, y hacemos uso del hecho de que\(g = diag(1,1,1)\), así que eso\(detg = 1\).) El resultado es

\[S_z = \epsilon _{xyz}u^x v^x = 1\]

como se esperaba. (Aquí no importa si hablamos\(S_z\) o\(S^z\), porque con esta métrica, subir y bajar índices no cambia los componentes de un vector.)

Clasificación de 3 superficies

Una aplicación útil del covector\(3\) -volumen es clasificar\(3\) -superficies por cómo se relacionan con el cono de luz. Si clava tres palos, todos en ángulo recto entre sí, entonces puedo considerarlos como un conjunto de vectores base que abarcan un espacio tridimensional de eventos. Este triespacio es flat, por lo que podemos llamarlo un hiperplano —o simplemente un plano si, como a lo largo de esta sección, no hay peligro de olvidar que tiene tres dimensiones en lugar de dos. Todos los eventos en este plano son simultáneos en mi marco de referencia. Ninguno de estos hechos depende del uso de ángulos rectos; solo tenemos que asegurarnos de que los palos no estén todos en el mismo plano.

El negocio de un físico es, en última instancia, hacer predicciones. Es decir, si se le da un conjunto de condiciones iniciales, podemos decir cómo evolucionará nuestro sistema a través del tiempo. Estas condiciones iniciales se miden en principio a lo largo de todo el espacio, y un plano de simultaneidad sería una elección natural para el conjunto de puntos en los que tomar las mediciones. Una superficie utilizada para este propósito se llama superficie Cauchy.

Si un plano es una superficie de simultaneidad según algún observador, entonces lo llamamos espacial. La línea mundial de cualquier partícula debe cruzarse con tal plano exactamente una vez, y es por eso que funciona como una superficie Cauchy: se nos garantiza detectar la partícula, para que podamos dar cuenta de su efecto en la evolución del cosmos. Podríamos tomar un avión espacial y reorientarlo. Para un cambio lo suficientemente pequeño en la orientación (es decir, un cambio que podría describirse por cambios suficientemente pequeños en los vectores base), seguirá siendo espacial.

Cuando un avión no es espacial, y permanece así bajo cualquier cambio de orientación suficientemente pequeño, lo llamamos timelike. En las coordenadas de Minkowski, un ejemplo sería el\(t-x-y\) avión. La línea mundial de una partícula dada podría nunca cruzar tal superficie y, por lo tanto, un plano similar al tiempo no se puede usar como superficie de Cauchy.

Un plano que no es ni espacial ni parecido al tiempo se llama parecido a la luz. Un ejemplo es la superficie definida por la ecuación\(x = t\) en las coordenadas de Minkowski.

La clasificación anterior se puede afirmar de manera muy sucinta utilizando el covector\(3\) -volumen definido anteriormente. Un plano es espacial, similar a la luz o al tiempo, respectivamente, si las regiones que contiene se describen mediante\(3\) covectores de volumen que son similares al tiempo, a la luz o al espacio. Una superficie lisa pero no necesariamente flat puede describirse localmente de acuerdo con estas categorías considerando su plano tangente. Por ejemplo, un cono de luz es parecido a la luz en cada uno de sus puntos, y como es parecido a la luz en todas partes, lo llamamos una superficie parecida a la luz. El horizonte de eventos de un agujero negro es también una superficie parecida a la luz. Cualquier superficie espacial, ya sea curva o flat, se puede utilizar como superficie Cauchy.

Las superficies parecidas a la luz tienen algunas propiedades divertidas. Usando la notación birdtracks, supongamos que formamos una superficie tal como el espacio abarcado por los tres vectores base\(\to a\),\(\to b\), y\(\to c\), y dejar que\(S \to \) sea el covector\(3\) -volumen correspondiente. La superficie es parecida a la luz, entonces

\[S \to S = 0\]

Porque\(S \to \) se define como la función que da el\(4\) -volumen de un paralelepípedo abarcado por las bases con un cuarto vector\(\to d\), y debido a que este volumen se desvanece cuando\(\to d\) es tangente a la superficie (propiedad V2), tenemos,

\[S \to a = S \to b = S \to c = 0\]

Entonces en este sentido\(S \to \) es perpendicular a la superficie. En el espacio euclidiano estamos acostumbrados a describir la orientación de una superficie en términos del vector normal unitario, y esto es muy cercano a lo que\(S \to \) es, excepto que es un covector más que un vector, y tampoco se puede hacer que tenga longitud unitaria, ya que su magnitud es cero. Podríamos arreglar el primero de estos dos problemas construyendo el vector\(\to S\) que es dual to\(S\to \), pero esto tiene un efecto desconcertante. Combinando\(\PageIndex{17}\) con la definición de\(S\to \), encontramos que\(\to S\) abarca un\(4\) volumen de fuga con los vectores base, y por lo tanto por V2 encontramos que\(\to S\) es tangente a la superficie. Así, en cierto sentido tenemos un vector que es a la vez paralelo y tangente a una superficie —lo que evita ser absurdo porque realmente nos estamos refiriendo a dos objetos diferentes, el covector\(S\to \) y el vector\(\to S\).