9.5: Congruencias, Expansión y Rigidez

Objetivos de aprendizaje

• Explicar las técnicas matemáticas para abordar los diferentes temas como expansión, rotación y cizallamiento

Figura\(\PageIndex{1}\): 1. No conservación. 2. Expansión. 3. Rotación. 4. Cizalla.

Este capítulo se ha centrado en los fluxes de cantidades conservadas; hemos querido descartar imágenes como la figura\(\PageIndex{1}\) (1), en las que la aparición y desaparición de las líneas mundiales implicaría la no conservación de propiedades como la carga y la masa-energía. Pero las técnicas matemáticas que hemos desarrollado resultan ser una manera elegante de abordar los diferentes temas descritos en las otras partes de la figura\(\PageIndex{1}\).

Congruencias

En la figura\(\PageIndex{1}\) (2), tenemos expansión. Por ejemplo, las líneas mundiales podrían representar galaxias que se separan más a causa de la expansión cosmológica resultante del Big Bang. No esperamos que los gobernantes se expandan o contraigan, en el sentido de que aunque un gobernante pueda exhibir contracción de Lorentz, siempre debe tener la misma longitud en su propio marco de descanso a menos que haya sido mecánicamente estresado o alterado.

Si hay más de una dimensión espacial, entonces podemos tener rotación, como en la figura\(\PageIndex{1}\) (3). Estas líneas mundiales podrían representar una constelación de satélites orbitantes, o puntos fijos en un laboratorio giratorio.

La otra posibilidad interesante, si hay más de una dimensión espacial, es el cizallamiento, figura\(\PageIndex{1}\) (4). Aquí el grupo rectangular de cuatro partículas se contrae en una dirección mientras se expande en la otra para mantener constante el\(2\) volumen cerrado.

Para discutir estas posibilidades, es conveniente definir la noción de una congruencia similar al tiempo, que es un conjunto de líneas mundiales no intersecantes, suaves y similares al tiempo cuya unión constituye todos los eventos en alguna región del espacio-tiempo. Es decir, “llenamos” el espacio-tiempo con un número infinito de líneas mundiales para que no haya espacio entre ellas. Esto es algo así como la veta en un trozo de madera, o la concepción de Faraday de líneas de campo que llenan el espacio, excepto que una de nuestras\(n + 1\) dimensiones es similar al tiempo, y no se permite que las líneas apunten en direcciones que se encuentran fuera del cono de luz. Una forma de especificar una congruencia es dar el vector de velocidad normalizada que es tangente a la línea mundial que pasa por cualquier punto dado.

Ejemplo\(\PageIndex{1}\): An expanding congruence

Como ejemplo de congruencia en\(1+1\) dimensiones, considere el conjunto de todas las curvas de la forma\(x = ae^{bt}\), donde\(a\) y\(b\) son constantes positivas. Parecería figura\(\PageIndex{1}\) (2). Let

\[u = \frac{\mathrm{d} x}{\mathrm{d} t} = abe^{bt}\]

el vector de velocidad es

\[v^λ = γ^{-1} (1,u)\]

donde el factor de\(\gamma ^{-1} = \sqrt{1 - u^2}\) da la normalización adecuada\(v^λ v_λ = 1\).

Ejemplo\(\PageIndex{2}\): A boring congruence

Supongamos que en cambio dejamos que la congruencia consista en el conjunto de todas las curvas de la forma\(x = c + ut\), donde\(c\) y\(u\) son constantes y\(|u| < 1\). Entonces como en el ejemplo anterior,\(v^λ = γ^{-1} (1,u)\). Las líneas mundiales son inerciales y paralelas entre sí.

Expansión y rigidez

Para lo que resta de esta discusión, nos limitamos al caso\(1 + 1\) -dimensional, de manera que la rotación y el cizallamiento son imposibles, y la única pregunta interesante es si una congruencia dada tiene expansión. En\(1 + 1\) dimensiones, la congruencia se puede especificar dando la función\(u(x,t)\), donde como en los ejemplos anteriores,\(u = dx/dt\). Si\(u\) es constante, entonces tenemos ejemplo\(\PageIndex{2}\), y claramente no hay expansión. Por lo tanto, la expansión requiere que uno\(∂u/∂t\) o\(∂u/∂x\), o ambos, sean distintos de cero.

Figura\(\PageIndex{2}\): Una congruencia con\(∂u/∂x\) igual a cero. 2. Una congruencia con\(∂u/∂t = 0\). 3. Una congruencia sin expansión.

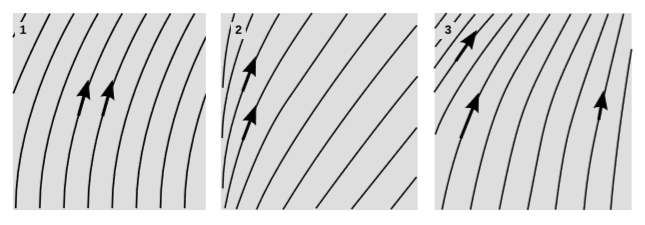
La figura\(\PageIndex{1}\) (1) muestra el caso donde\(∂u/∂x = 0\) y\(∂u/∂t \neq 0\). Cada línea del mundo es una copia de las otras que se han desplazado espacialmente, y los dos vectores de velocidad mostrados como flechas son iguales. Esta es precisamente la paradoja de la nave espacial de Bell (sección 3.9). Si bien el espaciado horizontal entre las líneas del mundo permanece constante según lo definido por el marco fijo de referencia utilizado para el diagrama, un observador que acelera junto con una de las partículas encontraría que se habían expandido alejándose una de la otra, porque las barras métricas del observador tienen Lorentz contraída. Esta es una expansión real en el sentido de que si las líneas del mundo son partículas en un objeto sólido, el objeto se encuentra bajo una tensión creciente.

En la figura\(\PageIndex{2}\) (2) tenemos\(∂u/∂t = 0\) y\(∂u/∂x \neq 0\). Las líneas mundiales son copias unas de otras que se han desplazado temporalmente. Los dos vectores de velocidad en el diagrama son los mismos. Todas las partículas comenzaron a acelerarse desde el mismo punto en el espacio, pero en diferentes momentos. Aquí hay claramente una expansión, porque las líneas mundiales se están separando más.

Supongamos que aceleramos un objeto rígido como una regla. Entonces debemos tener algo así como la figura\(\PageIndex{2}\) (3). Para evitar las situaciones descritas en\(\PageIndex{2}\) (1) y\(\PageIndex{2}\) (2), el vector de velocidad debe variar con ambos\(t\) y\(x\); los tres vectores de velocidad en la figura son todos diferentes. A medida que las partículas se aceleran, el espaciamiento entre ellas se contrae Lorentz, de modo que un observador que acelera junto con ellas ve el espaciado como constante restante.

Esta noción de movimiento rígido en la relatividad se llama rigidez Born. Ninguna sustancia física puede ser naturalmente perfectamente rígida (Born rígida), porque si lo fuera, entonces la velocidad a la que viajaron las ondas sonoras en ella sería mayor que c. La rigidez nacida solo se puede lograr a través de un conjunto de fuerzas externas aplicadas en todos los puntos sobre el objeto de acuerdo con un programa que se ha planeado de antemano. Un objeto real como una regla no mantiene su propia rigidez Nacida, pero eventualmente volverá a su tamaño y forma originales después de haber sufrido una aceleración relativista, debido a sus propias propiedades elásticas, siempre que la aceleración haya sido lo suficientemente suave como para evitar dañarlo permanentemente. En\(1+1\) dimensiones, la rigidez del Born equivale a una falta de expansión. En\(3 + 1\) dimensiones, también requerimos cizallamiento de fuga.

Matemáticamente, es claro que la condición de expansión desaparecida debe ser expresable en\(1 + 1\) dimensiones en términos de las derivadas parciales\(∂u/∂t\) y\(∂u/∂x\), y dado que hemos podido describir la condición de manera independiente del marco (refiriéndola a observaciones realizadas por el comoving observador), también debería ser algo que podamos expresar como escalar dentro de la gramática de la gimnasia índice. Solo hay una manera posible de expresar tal condición, que es

\[∂_a v^a = 0\]

De hecho, podemos definir un escalar\(Θ\), llamado escalar de expansión, según

\[Θ = ∂_a v^a\]

Esta definición es válida en\(n+1\) dimensiones, pero en\(1+1\) dimensiones reduce a

\[\Theta = \frac{\partial \gamma }{\partial t} + \frac{\partial (u\gamma )}{\partial x}\]

El escalar de expansión se interpreta como la tasa fraccionaria de cambio en el volumen de un conjunto de partículas que se mueven a lo largo de las líneas del mundo definidas por la congruencia, donde la tasa de cambio se define con respecto al tiempo adecuado\(τ\) de un observador que se mueve junto con las partículas. Por ejemplo, la expansión cosmológica conduce a un aumento fraccionario en las distancias entre galaxias\(∆L/L\) que, por un pequeño intervalo de tiempo\(∆τ\), es igual a\(H_o∆τ\), donde\(H_o\), llamada constante de Hubble, se trata\(2.3×10^{-18}\; s^{-1}\). Es decir, la tasa fraccionaria de cambio es\((1/L)dL/dτ = H_o\). Debido a que las distancias se expanden en las tres dimensiones espaciales, la tasa fraccional de cambio de volumen es

\[\Theta = \frac{1}{V}\frac{\mathrm{d} V}{\mathrm{d} \tau } = 3H_o\]

En este ejemplo, el espacio-tiempo no es flat, por lo que tendríamos que expresarnos\(Θ\) en términos de la derivada covariante\(∇_a\) definida en la sección 9.4, no la derivada parcial\(∂a\).

Ejemplo\(\PageIndex{3}\): A catastrophe

Figura\(\PageIndex{3}\): Una catástrofe

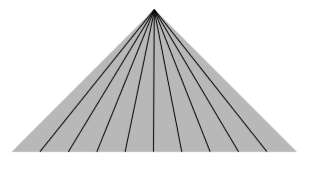
Considera la congruencia temporal en\(1+1\) las dimensiones definidas por\(u = x/t\). Este consiste en el conjunto de todas las líneas mundiales inerciales que pasan por el origen. Dado que nuestra definición de congruencia requiere que las líneas del mundo no se intersecten, limitemos este ejemplo al interior del cono de luz pasado del origen,\(|x| < -t\). Tenemos un universo lleno de partículas desventuradas, todas dirigiéndose como lemmings hacia una colisión catastrófica. El diagrama espacio-tiempo parece un diagrama de rayos ópticos para la formación de una imagen real. Un cálculo da el resultado inesperadamente simple\(Θ = γ/t\). Porque\(t < 0\), esto es negativo, lo que indica una contracción, y sopla hasta menos el infinito a medida que\(t\) se acerca\(0\).

Cáusticos

El ápice del cono en el ejemplo\(\PageIndex{3}\) es un cáustico. Dado un conjunto de líneas rectas de vuelo espacial, se produce un cáustico donde su intensidad diverge hasta el infinito. La palabra significa “quemar”, porque en la óptica un cáustico de los rayos de luz concentra la energía y puede quemar cosas. \(\PageIndex{3}\)El ejemplo involucra una cáustica de líneas mundiales similares al tiempo, y “recto” debe interpretarse en el sentido de que las líneas mundiales son inerciales.

Figura\(\PageIndex{4}\): Un cáustico en las líneas de simultaneidad de la familia de líneas mundiales aceleradas.

La figura\(\PageIndex{4}\) muestra dos cáusticos formados por líneas espaciales para el sistema de coordenadas aceleradas descrito en la sección 7.1. Aquí, como suele ser el caso, los cáusticos no son solo puntos.

Un ejemplo de la relatividad general es que cuando se forma un agujero negro por colapso gravitacional, un cáustico se forma en un punto por el conjunto de líneas mundiales parecidas a la luz que ingresan al horizonte de eventos desde el universo exterior en el momento en que se forma el horizonte. Si se emite un rayo de luz desde este punto cáustico, permanece en el horizonte de eventos para siempre, al igual que todos los rayos emitidos en el horizonte en dirección hacia afuera en momentos posteriores. El horizonte de eventos es el mismo conjunto de eventos que la unión de todas las líneas mundiales parecidas a la luz que entran en el horizonte en el cáustico. ⁴

El teorema de Herglotz-Noether en 1+1 dimensiones

Ciertos tipos de movimiento nacido-rígidos son posibles, y otros no lo son, puramente como una cuestión de cinemática. Resulta posible acelerar una varilla de una manera Nacido-rígida a lo largo de su propia longitud, pero sorprendentemente, no es posible, por ejemplo, que una esfera permanezca Nacido-rígida mientras gira simultáneamente y tiene su centro de masa acelerado. Los posibles tipos de movimiento son delineados por un teorema llamado teorema de Herglotz-Noether. A diferencia de la versión\(3+1\) -dimensional del teorema, la versión\(1+1\) -dimensional no es sorprendente ni difícil de afirmar o probar.

Teorema de Herglotz-Noether en\(1+1\) dimensiones: Cualquier movimiento rígido en\(1 + 1\) las dimensiones está determinado únicamente por la línea mundial\(W\) de un punto, siempre que la línea mundial de ese punto sea suave y similar al tiempo. En general sólo es posible extender la congruencia que describe el movimiento a algún barrio de\(W\).

Prueba

Para evitar problemas técnicos, asumimos que “suave” significa analítico, lo que debilita ligeramente el resultado. Como se discutió anteriormente, la expansión cero es equivalente a\(0 = \frac{\partial \gamma }{\partial t} + \frac{\partial (u\gamma )}{\partial x}\), donde\((t,x)\) están cualquier conjunto de coordenadas de Minkowski. Esto se puede poner en la forma\(\frac{\partial u}{\partial x} = f(u) \frac{\partial u}{\partial t}\), donde\(f\) es suave para\(-1 < u < 1\) y\(f(0) = 0\). Tenemos que demostrar que la solución de esta ecuación diferencial parcial, si existe, es única dada\(W\). Elegimos arbitrariamente un evento en\(W\). Por supuesto,\(W\) es timelike en este punto, así que somos libres de elegir nuestras coordenadas Minkowski de tal manera que nuestro punto esté en reposo en este evento en el origen. Ya que\(f(0) = 0\), se deduce que en el origen\(∂u/∂x = 0\). De manera similar podemos evaluar las derivadas superiores\(∂^n u/∂x^n\), y debido a que\(u\) es suave podemos en este cálculo intercambiar libremente el orden de las derivadas parciales\(∂x\) y\(∂t\). Es sencillo demostrar que estos derivados superiores también\(∂^n u/∂x^n\) son cero. Dado que\(u(x)\) se supone que es analítico, se deduce que\(u(0,x) = 0\) para todos\(x\), es decir, un observador que se mueve instantáneamente\(W\) a lo largo\(t = 0\) dice que todos los demás puntos están en reposo también en ese momento. Pero debido a que\(W\) es parecido al tiempo, siempre podemos encontrar algún vecindario\(A\) de\(W\) tal manera que cada punto en\(A\) sea simultáneo con un evento único\(W\) según un observador en ese evento moviéndose junto con\(W\). Por lo tanto, el valor de\(u\) se determina en todas partes\(A\), y esto completa la prueba de que la congruencia existe y es única en\(A\).

Observaciones

1. La versión\(1 + 1\) -dimensional del teorema de Herglotz-Noether no es un caso especial de la versión\(3 + 1\) -dimensional. Este último suele ser probado para una congruencia de relleno de espacio, y falla cuando el cuerpo en cuestión no encierra un volumen, por ejemplo, en el caso de una varilla delgada o una letra “C”.
2. El teorema puede fortalecerse relajando el requerimiento de suavidad para que solo se requiera la existencia de una segunda derivada de la posición con respecto al tiempo adecuado. ⁵
3. Si el movimiento se acelera, entonces el movimiento rígido no se puede extender a una distancia arbitraria de\(W\). Si la aceleración adecuada de\(W\) puede ser tan grande como una, entonces como en el ejemplo?? , p.?? , esperamos poder extender el movimiento rígido a una distancia adecuada sólo tan grande como\(c^2/a\), donde habrá un cáustico similar al de la figura\(\PageIndex{4}\).

La paradoja de la nave espacial de Bell revisitada

La paradoja de la nave espacial de Bell se discutió en la sección 3.9. En la paradoja, dos naves espaciales comienzan a acelerar simultáneamente y tienen aceleraciones iguales en el marco de un observador externo, inercial, provocando que un hilo estirado entre ellas se rompa. Ahora damos una demostración más rigurosa y matemáticamente elegante del mismo resultado, sugerida por P. Allen.

El movimiento del hilo a lo largo de su longitud puede describirse mediante una congruencia similar al tiempo. Si el hilo no va a caer bajo ninguna tensión, entonces esta debe ser una congruencia Nacido-rígida. Por el teorema\(1+1\) -dimensional de Herglotz-Noether, la congruencia está determinada de manera única por el movimiento de uno de sus puntos, que tomamos como el cohete trasero. Esta congruencia pasa a ser conocida. Se define por el sistema de coordenadas aceleradas (coordenadas de Rindler) descrito en la sección 7.1. La desaparición del escalar de expansión para esta congruencia se deja para que el lector verifique. Pero esta congruencia consiste en líneas mundiales cuyas aceleraciones adecuadas son cada una constante y todas diferentes entre sí, y esto es inconsistente con la descripción dada en la paradoja de Bell, donde se afirma que existe un marco en el que los movimientos de las dos naves son idénticos a excepción de una traducción. Por lo tanto, el hilo no puede moverse rígidamente.

Esto completa la resolución de la paradoja, pero como ejemplo ilustrativo, presentamos un cálculo explícito del escalar de expansión para la congruencia que uno imaginaría más naturalmente que se implicaría en la descripción de la paradoja. Esto viene dado por\((x + c)^2 = 1 + t^2\). Para un valor dado del parámetro\(c\), obtenemos una línea mundial acelerada. (Su aceleración adecuada\(a = 1\) pasa a ser constante, aunque esto no es necesario para los fines de discutir la paradoja). Cada línea mundial comienza en reposo en\(t = 0\), y cada una tiene la misma aceleración en cualquier momento\(t\). Al elegir dos valores distintos\(c\) como puntos finales del hilo, obtenemos la situación literal descrita en la paradoja.

La diferenciación implícita da\(u = \frac{t}{\sqrt{1 + t^2}}\). El álgebra se vuelve un poco desordenado ahora, así que utilicé el sistema de álgebra informática de código abierto Maxima. El siguiente programa, que debería ser bastante legible sin conocimiento previo de la sintaxis de Maxima, calcula el tensor de expansión:

1. u:t/sqrt (1+t^2);
2. gamma:1/sqrt (1-u^2);
3. theta:diff (gamma, t) +diff (u*gamma, x);
4. es (igual (theta, gamma*u^2/t));

La tercera línea imprime una expresión complicada para\(Θ\), que la cuarta línea muestra se puede simplificar a\(γu^2/t\). Esto es positivo para\(t > 0\), lo que demuestra que el hilo se ve obligado a expandirse. Obsérvese que aunque el cálculo se realizó en un conjunto particular de coordenadas, un escalar relativista como\(Θ\) tiene un valor independiente de coordenadas. La referencia a un determinado sistema de coordenadas o marco de referencia se da únicamente en la definición inicial de la congruencia, la cual se define para modelar la situación descrita en la paradoja, la cual se afirma en términos de un observador externo particular.

Referencias

¹ Penrose, 1968. La prueba se presenta en Misner, Thorne y Wheeler, p. 924

² 5Giulini, “La rica estructura del espacio Minkowski”, arxiv.org/abs/0802. 4345, teoremas 18 y 22