3.3: Nociones afines y transporte paralelo

El parámetro afín en el espacio-tiempo curvo: un boceto aproximado

Queremos poder medir las cosas en el espacio-tiempo curvo. Resulta que existen dos sistemas complementarios de medición que podemos aplicar: medida afín y medida métrica. La medida afín en geometría plana se introdujo en la Sección 2.1. Sorprendentemente, resulta ser bastante fácil generalizar esto a la caja curva. Nuestra construcción del parámetro afín con un andamiaje de paralelogramos dependía de la existencia y singularidad de paralelismos expresados por el axioma A1, por lo que podríamos imaginar que no tenía sentido intentar generalizar la construcción al espacio-tiempo curvo. Pero el principio de equivalencia nos dice que el espacio-tiempo está afín localmente a alguna aproximación. Concretamente, el tiempo-reloj es un ejemplo de un parámetro afín, y la curvatura del espacio-tiempo claramente no puede impedirnos construir un reloj y liberarlo en una trayectoria de caída libre.

De manera más general, podemos usar el hecho de que cada segmento de un geodésico es geométricamente similar a cualquier otro segmento. Por ejemplo, considere un arco del ecuador terrestre que abarca un grado de longitud. Ese arco podría deslizarse a lo largo del ecuador hasta una ubicación diferente, luego expandirse para cubrir 3 grados de longitud. Los dos arcos son similares.

Ejemplo 2: Las geodésicas son especiales

Los siguientes tres no ejemplos muestran que esta es una propiedad especial de la geodésica.

La propiedad no es disfrutada por una curva no geodésica. Un segmento de un pentágono que abarca uno de los vértices no es similar a algún otro segmento que sea recto.

Otro no ejemplo que involucra no geodésicas es la curva que obtenemos en 1+1-dimensional espacio-tiempo uniendo el eje x positivo y el eje t positivo. Nunca podemos tomar un segmento de un año del eje t y, a través de cualquier combinación de refuerzos y rotaciones, hacerlo coincidir con una pieza de un año luz del eje x. El segmento original es similar al tiempo, y cualquier impulso o rotación conservará su carácter de tiempo.

Además, no es cierto en general, cuando existe curvatura, que podamos tomar cualquier figura geométrica, transportarla a donde queramos, y también escalarla como queramos. Por ejemplo, la geometría euclidiana es una buena aproximación en pequeñas porciones de la superficie esférica de la Tierra, por lo que se puede hacer una hoja de ruta en forma de rectángulo con cuatro esquinas en ángulo recto. Sin embargo, no es posible escalar dicho rectángulo; para mapear una gran parte del mundo, tenemos que introducir distorsiones del tipo utilizado en las proyecciones de mapas.

Debido a que los geodésicos tienen esta propiedad especial, podemos deslizar cualquier porción de un geodésico a cualquier otro lugar de la geodésica y emplearla como estándar de medida. Esto nos da un sistema completo de medición a lo largo de esa geodésica, y funciona independientemente de si la geodésica es similar al tiempo, a la luz o al espacio. Pero como en la geometría plana, la medición afín no nos permite comparar longitudes a lo largo de una geodésica con longitudes a lo largo de otra.

El parámetro afín con más detalle

Cuando originalmente definimos la medida afín en la Sección 2.1, para un espacio plano, lo hicimos a través de la construcción explícita de un andamio. Un ejemplo importante de la naturaleza diferencial, es decir, local, de nuestra geometría es la generalización de la construcción de andamios desde un contexto más amplio que la geometría afín.

Para generalizar la receta para la construcción (Figura 3.2.1), el primer obstáculo es la ambigüedad de la instrucción para construir paralelogramo\((0,1,q_0,q_1)\), lo que nos obliga a dibujar 1q ₁ paralelo a 0q ₀. Supongamos que interpretamos esto como una instrucción para hacer los dos segmentos inicialmente paralelos, es decir, paralelos a medida que salen de la línea en 0 y 1. Para cuando lleguen a q ₀ y q ₁, pueden estar convergiendo o divergiendo.

Figura\(\PageIndex{1}\) - Construcción de un parámetro afín en espacio-tiempo curvo.

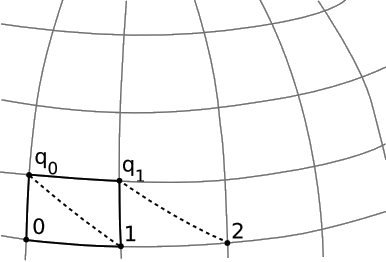
Debido a que el paralelismo es solamente aproximado aquí, habrá cierta cantidad de error en la construcción del parámetro afín. Una forma de detectar tal error es que las celosías construidas con diferentes distancias iniciales salgan de escalonamiento entre sí. Por ejemplo, podemos definir\(\frac{1}{2}\) como antes requiriendo que la celosía construida con el segmento inicial 0 se\(\frac{1}{2}\) alinee con la celosía original en 1. Encontraremos, sin embargo, que no se alinean del todo en otros puntos, como el 2. Usemos esta discrepancia\(\epsilon\) = 2 − 2' como medida numérica del error. Dependerá tanto\(\delta_{1}\) de la distancia 01, como de\(\delta_{2}\), de la distancia entre 0 y q ₀. Dado que\(\epsilon\) desaparece para\(\delta_{1}\) = 0 o\(\delta_{2}\) = 0, y dado que el principio de equivalencia garantiza un comportamiento suave en escalas pequeñas, el término principal en el error será en general proporcional al producto\(\delta_{1} \delta_{2}\). En el lenguaje de los infinitesimales, podemos sustituir\(\delta_{1}\) y\(\delta_{2}\) con distancias infinitesimalmente cortas, que por simplicidad asumimos que son iguales, y que llamamos d\(\lambda\). Entonces el parámetro afín\(\lambda\) se define como\(\lambda = \int d \lambda\), donde el error de orden d\(\lambda^{2}\) es, como de costumbre, interpretado como la despreciable discrepancia entre la integral y su aproximación como una suma de Riemann.

Transporte paralelo

Si estuviste alerta, te habrás dado cuenta de que te engañé en un punto crucial de esta construcción. Íbamos a hacer 1q ₁ y 0q ₀ “inicialmente paralelos” ya que dejaron 01. ¿Cómo deberíamos siquiera definir esta idea de “inicialmente paralela”? Podríamos intentar hacerlo haciendo iguales los ángulos q ₀ 01 y q ₁ 12, pero esto no funciona del todo, porque no especifica si el ángulo es a la izquierda o a la derecha en el plano bidimensional de la página. En tres o más dimensiones, el tema se vuelve aún más grave. Los trabajadores de la construcción que construyen la celosía necesitan mantenerlo todo en un solo plano, pero ¿cómo lo hacen en el espacio-tiempo curvo?

La respuesta de un matemático sería que nuestra geometría carece de alguna estructura adicional llamada conexión, que es una regla que especifica cómo un vecindario localmente plano debe unirse sin problemas a otro vecindario localmente plano cercano. Si alguna vez compraste dos mapas e intentaste grabarlos juntos para hacer un mapa grande, has formado una conexión. Si los mapas estuvieran a una escala suficientemente grande, probablemente también notaste que esto era imposible de hacer a la perfección, debido a la curvatura de la tierra.

Físicamente, la idea es que en el espacio-tiempo plano, es posible construir sistemas de guía inercial como los discutidos anteriormente. Como son posibles en el espacio-tiempo plano, también son posibles en barrios localmente planos del espacio-tiempo, y luego pueden ser transportados de un barrio a otro. En tres dimensiones espaciales, el vector de momento angular de un giroscopio mantiene su dirección, y podemos orientar otros vectores, como 1q ₁, en relación con él. Supongamos para concreción que la construcción del parámetro afín anterior se está llevando a cabo en tres dimensiones espaciales. Colocamos un giroscopio en 0, orientamos su eje a lo largo de 0q ₀, lo deslizamos a lo largo de la línea hasta 1, y luego construimos 1q ₁ a lo largo de ese eje.

En 3+1 dimensiones, un giroscopio solo hace parte del trabajo. Ahora tenemos que mantener la dirección de un vector de cuatro dimensiones. Cuatro vectores no se discutirán en detalle hasta la sección 4.2, pero se pueden usar dispositivos similares para mantener sus orientaciones en el espacio-tiempo. Estos dispositivos físicos son formas de definir una noción matemática conocida como transporte paralelo, que nos permite llevar un vector de un punto a otro en el espacio. En general, especificar una noción de transporte paralelo equivale a especificar una conexión.

El transporte paralelo depende de la trayectoria, como se muestra en la Figura 3.2.2.

Figura\(\PageIndex{2}\) - El transporte paralelo depende de la ruta. En la superficie de esta esfera, el transporte paralelo de un vector a lo largo de ABC da una respuesta diferente a transportarlo a lo largo de AC.

Parámetros afines definidos solo a lo largo de geodésicas

En el contexto del espacio-tiempo plano, el parámetro afín se definió solo a lo largo de líneas, no curvas arbitrarias, y no pudo compararse entre líneas que discurren en diferentes direcciones. En el espacio-tiempo curvo está presente la misma limitación, pero con “a lo largo de líneas” reemplazado por “a lo largo de la geodésica”. La Figura 3.2.3 muestra lo que sale mal si tratamos de aplicar la construcción a una línea mundial que no es geodésica. Una definición de geodésico es que es el curso que terminaremos siguiendo si navegamos manteniendo un rumbo fijo relativo a un dispositivo de guía inercial como el giroscopio; es decir, la tangente a un geodésico, cuando se transporta en paralelo más a lo largo del geodésico, sigue siendo tangente. Una curva no geodésica carece de esta propiedad, y el efecto sobre la construcción del parámetro afín es que los segmentos nq _n se desalinean cada vez más con la curva.

Figura 3.2.2. El transporte paralelo no conserva el ángulo de los vectores con respecto a la curva, como lo haría con un geodésico. Los errores en la construcción estallan de una manera que no sucedería si la curva hubiera sido geodésica. El cuarto paralelo discontinuo vuela salvajemente alrededor de la parte posterior de la esfera, envolviéndose y encontrándose con la curva en un punto, 4, que es esencialmente aleatorio.