3.4: Modelos

Una primera reacción típica a la frase “espacio-tiempo curvo” —o incluso “espacio curvo”, para el caso— es que suena como una tontería. ¿Cómo se puede curvar o distorsionar el espacio vacío sin rasgos? El concepto de distorsión parecería implicar tomar todos los puntos y empujarlos en diversas direcciones como en una pintura de Picasso, de manera que se alteran las distancias entre puntos. Pero si el espacio no tiene abolladuras o rasguños identificables, parecería imposible determinar qué puntos antiguos se habían enviado a qué nuevos puntos, y la distorsión no tendría ningún efecto observable en absoluto. ¿Por qué deberíamos esperar poder construir geometría diferencial sobre una base tan lógicamente dudosa? En efecto, históricamente, diversos matemáticos han tenido fuertes dudas sobre la autoconsistencia lógica tanto de la geometría no euclidiana como de los infinitesimales. E incluso si una fuente autorizada te asegura que el sistema resultante es autoconsistente, su naturaleza misteriosa y abstracta parecería hacerte difícil desarrollar cualquier imagen de trabajo de la teoría que pueda desempeñar el papel que juegan los bocetos mentales de las gráficas en la organización de tus conocimientos de cálculo.

Figura\(\PageIndex{1}\) - Tullio Levi-Civita (1873- 1941) trabajó en modelos de sistemas numéricos que poseen infinitesimales y en geometría diferencial. Inventó la notación tensora, que Einstein aprendió de su libro de texto. Fue nombrado para prestigiosas cátedras dotadas en Padua y la Universidad de Roma, pero fue despedido en 1938 por ser judío y antifascista.

Los modelos proporcionan una forma de tratar tanto las cuestiones lógicas como las conceptuales. Figura 3.2.1 “salta” de la página, presentando una fuerte impresión psicológica de una superficie curva renderizada en perspectiva. Esto sugiere encontrar un objeto matemático real, como una superficie curva, que satisfaga todos los axiomas de un determinado sistema lógico, como la geometría no euclidiana. Tenga en cuenta que el modelo puede contener elementos extrínsecos, como la existencia de una tercera dimensión, que no están conectados al sistema que se está modelando.

Centrémonos primero en la consistencia. En general, ¿qué podemos decir sobre la autoconsistencia de un sistema matemático? Para empezar, nunca podemos probar nada sobre la consistencia o falta de consistencia de algo que no es un sistema formal bien definido, por ejemplo, la Biblia. Incluso Elementos de Euclides, que fue un modelo de rigor formal durante miles de años, es lo suficientemente flojo como para permitir una ambigüedad considerable. Si te inclinas a burlarte de los tontos matemáticos renacentistas que seguían tratando de probar el postulado paralelo E5 a partir de los postulados E1-E4, considera el siguiente argumento. Supongamos que reemplazamos E5 por E5', que establece que los paralelos no existen: dada una línea y un punto que no está en la línea, nunca se puede dibujar ninguna línea a través del punto y paralela a la línea dada. En el nuevo sistema de geometría plana E' que consiste en E1-E4 más E5', podemos probar una variedad de teoremas, y uno de ellos es que hay un límite superior en el área de cualquier figura. Esto impone un límite al tamaño de los círculos, y eso parece contradecir al E3, que dice que podemos construir un círculo con cualquier radio.

Por lo tanto, concluimos que E' carece de autoconsistencia. ¡Uy! Como su texto de geometría de secundaria indudablemente mencionó de pasada, E' es un sistema perfectamente respetable llamado geometría elíptica. Entonces, ¿qué tiene de malo esta supuesta prueba de su falta de autoconsistencia? El tema es el enunciado exacto del E3. E3 no dice que podamos construir un círculo dado cualquier número real como su radio. Euclides no pudo haber pretendido ninguna interpretación de ese tipo, ya que no tenía noción de números reales. Para Euclides, la geometría era primaria y los números eran objetos construidos geométricamente, representándose como longitudes, ángulos, áreas y volúmenes. Una traducción literal de la declaración del axioma de Euclides es “Describir un círculo con cualquier centro y distancia”. ¹ “Distancia” significa un segmento de línea. Por lo tanto, no hay contradicción en E', porque E' tiene un límite en las longitudes de los segmentos de línea.

Ahora supongamos que tales ambigüedades han sido eliminadas de las definiciones y axiomas básicos del sistema. En general, esperamos que sea más fácil probar la inconsistencia de un sistema inconsistente que demostrar la consistencia de uno consistente. En el primer caso, podemos comenzar a arrancar teoremas, y si podemos encontrar la manera de probar tanto la proposición P como su negación ¬P, entonces obviamente algo anda mal con el sistema. Uno podría preguntarse si tal contradicción podría permanecer contenida dentro de una esquina del sistema, como los desechos nucleares. No puede La lógica aristotélica permite la prueba por contradicción: si probamos tanto P como ¬P con base en ciertas suposiciones, entonces nuestras suposiciones deben haber sido equivocadas. Si podemos probar tanto P como ¬P sin hacer suposiciones, entonces la prueba por contradicción nos permite establecer la verdad de cualquier proposición elegida al azar. Así, una sola contradicción es suficiente, en la lógica aristotélica, para invalidar todo el sistema. Esto va por la rúbrica latina ex falso quodlibet, que significa “de una falsedad, lo que quieras”. Así, cualquier contradicción demuestra la inconsistencia de todo el sistema.

Demostrar consistencia es más difícil. Si eres matemáticamente sofisticado, puedes estar tentado a dar un salto directo al teorema de Gödel, y afirmar que nadie puede probar la autoconsistencia de un sistema matemático. Esto sería una mala aplicación de Gödel. El teorema de Gödel solo se aplica a sistemas matemáticos que cumplen ciertos criterios técnicos, y algunos de los sistemas interesantes con los que estamos tratando no cumplen con esos criterios; en particular, el teorema de Gödel no se aplica a la geometría euclidiana, y Tarski y su estudiantes alrededor de 1950. Además, generalmente no requerimos una prueba absoluta de autoconsistencia. Por lo general, estamos satisfechos si podemos demostrar que cierto sistema, como la geometría elíptica, es al menos tan autoconsistente como otro sistema, como la geometría euclidiana. A esto se le llama equiconsistencia. La técnica general para demostrar la equiconsistencia de dos teorías es mostrar que un modelo de una puede construirse dentro de la otra.

Supongamos, por ejemplo, que construimos una geometría en la que el espacio de puntos es la superficie de una esfera, y se entiende que las líneas son las geodésicas, es decir, los grandes círculos cuyos centros coinciden en el centro de la esfera. Esta geometría, llamada geometría esférica, es útil en cartografía y navegación. Es no euclidiana, como podemos demostrar exhibiendo al menos una proposición que es falsa en la geometría euclidiana. Por ejemplo, construya un triángulo en la superficie terrestre con una esquina en el polo norte, y las otras dos en el ecuador, separadas por 90 grados de longitud. La suma de sus ángulos interiores es de 270 grados, contradiciendo Euclides, libro I, proposición 32. Por lo tanto, la geometría esférica debe violar al menos uno de los axiomas E1-E5, y de hecho viola tanto E1 (porque ninguna línea única está determinada por dos puntos antípodas como los polos norte y sur) y E5 (porque los paralelos no existen en absoluto).

Una construcción estrechamente relacionada da un modelo de geometría elíptica, en el que E1 se sostiene, y solo E5 es arrojado por la borda. Para lograr esto, modelamos un punto usando un diámetro de la esfera, ² y una línea como el conjunto de todos los diámetros que se encuentran en un plano determinado. Esto tiene el efecto de identificar puntos antípodas, de manera que ahora no hay violación a E1. En términos generales, esto es como cortarse la mitad de la esfera, pero hacer que los bordes se envuelvan. Dado que este modelo de geometría elíptica está incrustado dentro de un espacio euclidiano, todos los axiomas de geometría elíptica ahora pueden ser probados como teoremas en la geometría euclidiana. Si de ellos surgiera una contradicción, implicaría una contradicción en los axiomas de la geometría euclidiana. Concluimos que la geometría elíptica es equiconsistente con la geometría euclidiana. Esto se conocía mucho antes de la prueba de Tarski de 1950 de la autoconsistencia de la geometría euclidiana, pero como nadie estaba perdiendo el sueño por contradicciones ocultas en la geometría euclidiana, los matemáticos dejaron de perder el tiempo buscando contradicciones en la geometría elíptica.

Nota

El término “elíptico” puede ser algo engañoso aquí. El modelo todavía se construye a partir de una esfera, no de un elipsoide.

Ejemplo 3: Infinitesimales

Considere el siguiente sistema axiomáticamente definido de números:

1. Es un campo, es decir, tiene suma, resta, multiplicación y división con las propiedades habituales.
2. Es una geometría ordenada en el sentido de O1-O4, y el orden se relaciona con la suma y la multiplicación de la manera habitual.
3. Existencia de infinitesimales: Existe un número positivo d tal que d < 1, d < 1/2, d < 1/3,.

Un modelo de este sistema se puede construir dentro del sistema de números reales definiendo d como la función de identidad d (x) = x y formando el conjunto de funciones de la forma f (d) = P (d) /Q (d), donde P y Q son polinomios con coeficientes reales. El orden de las funciones f y g se define de acuerdo con el signo de\(\lim_{x \rightarrow 0^{+}}\) f (x) − g (x). Los axiomas 1-3 pueden probarse a partir de los axiomas de número real. Por lo tanto, este sistema, que incluye infinitesimales, es equiconsistente con los reales. Las construcciones más elaboradas pueden extender esto a sistemas que tienen más propiedades de los reales, y una calculadora basada en navegador que implementa dicho sistema está disponible en lightandmatter.com/calc/inf. Abraham Robinson extendió esto en 1966 a todos los análisis, y así no hay nada intrínsecamente no riguroso en hacer análisis al estilo de Gauss y Euler, con símbolos como dx que representan cantidades infinitesimalmente pequeñas. ³

---

³ Más sobre este tema está disponible en, por ejemplo, Cálculo elemental de Keisler: un enfoque infinitesimal, Una breve introducción al cálculo infinitesimal de Stroyan, o mi propio Cálculo, todos los cuales están disponibles de forma gratuita en línea.

Además de demostrar consistencia, estos modelos nos dan una idea de lo que está pasando. El modelo de geometría elíptica sugiere una idea de la razón de que existe un límite superior en longitudes y áreas: es porque el espacio se envuelve sobre sí mismo. El modelo de infinitesimales sugiere un hecho que no es inmediatamente obvio a partir de los axiomas: las cantidades infinitesimales componen una jerarquía, de manera que por ejemplo 7d está en proporción finita a d, mientras que d ² es como una “pulga menor” en el doggerel de Swift: “Las pulgas grandes tienen poca pulgas/ En sus espaldas para montarlos,/y las pulgas pequeñas tienen pulgas menores,/Y así, ad infinitum”.

La geometría esférica y elíptica no son modelos válidos de un espacio-tiempo general-relativista, ya que son localmente euclideanos en lugar de lorentzianos, pero aún nos brindan suficiente orientación conceptual para llegar a algunas ideas que de otra manera nunca se nos habrían ocurrido:

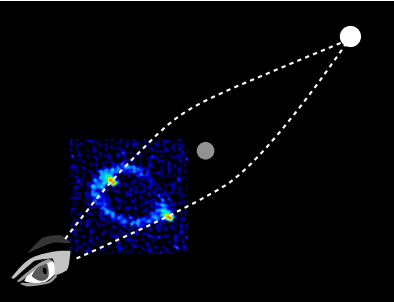
• En geometría esférica, podemos tener un polígono de dos lados llamado lune que encierra un área distinta de cero. En la relatividad general, una luna formada por las líneas mundiales de dos partículas representa un movimiento en el que las partículas se separan pero luego se reúnen, presumiblemente por alguna masa entre ellas que creó un campo gravitacional. Un ejemplo es la lente gravitacional.
• Ambos modelos esféricos se envuelven sobre sí mismos, de modo que no son topológicamente equivalentes a planos infinitos. Por lo tanto, formamos una conjetura de que puede haber un vínculo entre la curvatura, que es una propiedad local, y la topología, que es global. Tal conexión se observa efectivamente en la relatividad. Por ejemplo, las soluciones cosmológicas de las ecuaciones de la relatividad general vienen en dos sabores. Un tipo tiene suficiente materia en él para producir más de una cierta cantidad crítica de curvatura, y este tipo es topológicamente cerrado. Describe un universo que tiene volumen espacial finito, y que solo existirá por un tiempo finito antes de que se recontraiga en un Big Crunch. El otro tipo, correspondiente al universo que realmente habitamos, tiene un volumen espacial infinito, existirá por un tiempo infinito, y es topológicamente abierto.
• Hay una escala de distancia establecida por el tamaño de la esfera, siendo su inversa una medida de curvatura. En la relatividad general, esperamos que haya una manera similar de medir la curvatura numéricamente, aunque la curvatura puede variar de punto a punto.

Figura\(\PageIndex{2}\) - Un anillo de Einstein se forma cuando existe una alineación casual de una fuente distante con un cuerpo gravitante más cercano. Aquí, un cuásar, MG1131+0456, es visto como un anillo debido al enfoque de la luz por un objeto desconocido, posiblemente un agujero negro supermasivo. Debido a que toda la disposición carece de simetría axial perfecta, el anillo no es uniforme; la mayor parte de su brillo se concentra en dos grumos en lados opuestos. Este tipo de lentes gravitacionales es evidencia directa de la curvatura del espacio predicha por la lente gravitacional. Las dos geodésicas forman una lune, que es una figura que no puede existir en la geometría euclidiana.

Ejercicio\(\PageIndex{1}\)

Demostrar a partir de los axiomas E' que la geometría elíptica, a diferencia de la geometría esférica, no puede tener una luna con dos vértices distintos. Convénzase sin embargo, utilizando el modelo esférico de E', de que es posible en geometría elíptica que dos líneas encierren una región del espacio, en el sentido de que desde cualquier punto P de la región, un rayo emitido en cualquier dirección debe cruzarse con una de las dos líneas. Resumir estas observaciones con una caracterización de lunes en geometría elíptica versus lunes en geometría esférica.

Referencias

¹ Heath, pp. 195-202