5.6: Algunas estimaciones de orden de magnitud

Como propuesta general, calcular una estimación de orden de magnitud de un efecto físico requiere una comprensión del 50% de la física, mientras que un cálculo exacto requiere alrededor del 75%. ⁷ Hemos llegado al punto en el que es razonable intentar una variedad de estimaciones de orden de magnitud.

Nota

Esta afirmación es en sí misma sólo una estimación aproximada. Cualquiera que haya enseñado física sabe que los estudiantes suelen calcular un efecto exactamente sin comprender en absoluto la física subyacente.

El efecto geodésico

¿Cómo podríamos confirmar experimentalmente que el transporte paralelo alrededor de una trayectoria cerrada puede hacer que un vector gire? La rotación está relacionada con la cantidad de curvatura espacio-tiempo contenida dentro del camino, por lo que tendría sentido elegir un bucle que rodee un cuerpo gravitante. La rotación es un efecto puramente relativista, por lo que esperamos que sea pequeña. Para que sea más fácil de detectar, debemos dar la vuelta al bucle muchas veces, haciendo que el efecto se acumule. Esto es esencialmente una descripción de un cuerpo que orbita a otro cuerpo. Se espera que un giroscopio a bordo del cuerpo en órbita preceda. Esto se conoce como el efecto geodésico. En 1916, poco después de que Einstein publicara la teoría general de la relatividad, Willem de Sitter calculó el efecto sobre el sistema tierra-luna. El efecto no se verificó directamente hasta la década de 1980, y la primera medición de alta precisión fue en 2007, a partir del análisis de los resultados recolectados por el experimento satelital Gravity Probe B. La sonda portaba cuatro giroscopios hechos de cuarzo, que eran las esferas más perfectas jamás fabricadas, variando desde la esfericidad en no más de unos 40 átomos.

Figura\(\PageIndex{1}\) - El efecto geodésico medido por la sonda de gravedad B.

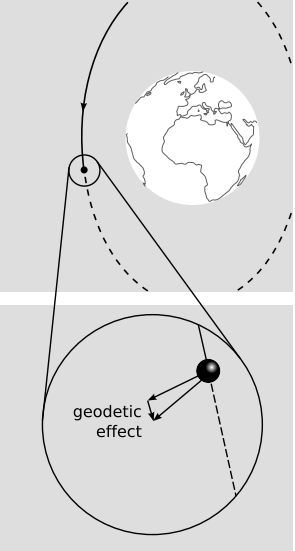
Estimemos el tamaño del efecto. La primera derivada de la métrica es, aproximadamente, el campo gravitacional, mientras que la segunda derivada tiene que ver con la curvatura. Por lo tanto, la curvatura del espacio-tiempo alrededor de la tierra debería variar como GMr ⁻³, donde M es la masa terrestre y G es la constante gravitacional. El área encerrada por una órbita circular es proporcional a r ², por lo que esperamos que el efecto geodésico varíe como\(\frac{nGM}{r}\), donde n es el número de órbitas. El ángulo de precesión es sin unidades, y la única manera de hacer que este resultado sea sin unidades es poner en un factor de\(\frac{1}{c^{2}}\). En unidades con c = 1, este factor es innecesario. En las unidades métricas ordinarias, el tiene sentido, porque\(\frac{1}{c^{2}}\) hace que el efecto puramente relativista salga a ser pequeño. El resultado, hasta factores sin unidad que no pretendíamos encontrar, es

\[\Delta \theta \sim \frac{nGM}{c^{2} r} \ldotp\]

También podríamos esperar una precesión de Thomas. Al igual que el efecto de curvatura espacio-tiempo, sería proporcional a\(\frac{nGM}{c^{2} r}\). Como no nos preocupamos por factores sin unidades, podemos simplemente agrupar la precesión de Thomas junto con el efecto ya calculado.

Los datos para la sonda de gravedad B son r = r _e + (650 km) y n ≈ 5000 (orbitando una vez cada 90 minutos para la duración de 353 días del experimento), dando\(\Delta \theta\) ∼ 3 × 10 ⁻⁶ radianes. La Figura 5.5.2 muestra los resultados reales ⁸ los cuatro giroscopios a bordo de la sonda. La precesión fue de aproximadamente 6 arco-segundos, o 3 × 10 ⁻⁵ radianes. Nuestra estimación bruta estaba en el orden correcto de magnitud. El factor sin unidades que falta en el lado derecho de la ecuación anterior es 3\(\pi\), lo que lleva a los dos resultados a un acuerdo cuantitativo bastante cercano. La derivación completa, incluyendo el factor 3\(\pi\), se da en la sección 6.2.

Figura_5.5.2b.png” />

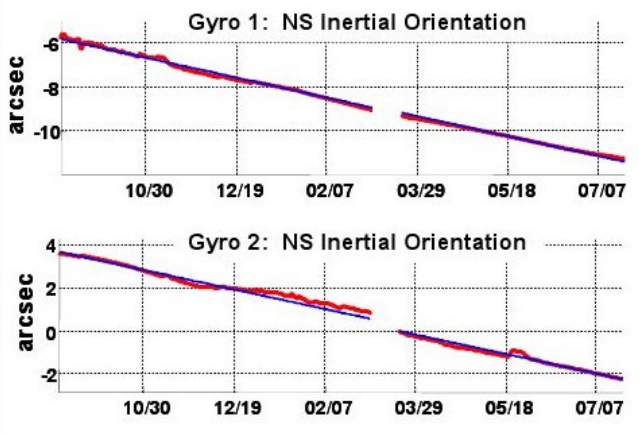
Figura\(\PageIndex{2}\) - Ángulo de precesión en función del tiempo medido por los cuatro giroscopios a bordo de Gravity Probe B.

Desviación de rayos de luz

En la discusión del vector momentum four en la sección 4.2, vimos que debido al principio de equivalencia, la luz debe verse afectada por la gravedad. Hay dos formas en que tal efecto podría ocurrir. La luz puede ganar y perder impulso a medida que viaja hacia arriba y hacia abajo en un campo gravitacional, o su vector de impulso puede ser desviado por un campo gravitacional transversal. Como ejemplo de este último, un rayo de luz estelar puede ser desviado por la gravedad del sol, haciendo que la posición aparente de la estrella en el cielo se desplace. La detección de este efecto fue una de las primeras pruebas experimentales de relatividad general. Por lo general, la luz brillante del sol haría imposible medir con precisión la ubicación de una estrella en la esfera celeste, pero este problema fue evitado por Arthur Eddington durante un eclipse de sol en 1919.

Estimemos el tamaño de este efecto. Ya hemos visto que el tensor Riemann es esencialmente solo una forma tensorial de escribir la curvatura gaussiana\(K = \frac{d \epsilon}{dA}\). Supongamos, por el bien de esta estimación aproximada, que el sol, la tierra y la estrella forman un triángulo no euclidiano con un ángulo recto en el sol. Entonces la deflexión angular es la misma que el defecto angular\(\epsilon\) de este triángulo, e iguala la integral de la curvatura sobre el interior del triángulo. Ignorando las constantes sin unidades, esto termina siendo exactamente el mismo cálculo que antes, y el resultado es\(\epsilon \sim \frac{GM}{c^{2} r}\), donde r es la distancia del rayo de luz de aproximación más cercana al sol. El valor de r no puede ser menor que el radio del sol, por lo que el tamaño máximo del efecto es del orden de\(\frac{GM}{c^{2} r}\), donde M es la masa del sol, y\(r\) es su radio. Encontramos\(\epsilon\) ∼ 10 ⁻⁵ radianes, o aproximadamente un segundo de arco. Medir la posición de una estrella dentro de un segundo arco estuvo bien dentro del estado del arte en 1919, en buenas condiciones en un cómodo observatorio. Esta observación, sin embargo, requirió que el equipo de Eddington viajara a la isla de Príncipe, frente a la costa de África Occidental. El clima estaba nublado, y sólo durante los últimos 10 segundos del eclipse de siete minutos el cielo se aclaró lo suficiente como para permitir tomar placas fotográficas del cúmulo estelar de Hyades contra el fondo del cielo oscurecido por el eclipse. La deflexión observada fue de 1.6 segundos de arco, de acuerdo con la predicción relativista. La predicción relativista se deriva en la sección 6.2.

Figura\(\PageIndex{3}\) - Una de las fotos de las observaciones de Eddington sobre el eclipse de 1919. Esto es un negativo fotográfico, por lo que el círculo que parece brillante es en realidad la cara oscura de la luna, y la zona oscura es realmente la corona brillante del sol. Las estrellas, marcadas por líneas arriba y debajo de ellas, aparecieron en posiciones ligeramente distintas a las normales, indicando que su luz había sido doblada por la gravedad del sol en su camino hacia nuestro planeta.

Referencias

⁸ arxiv.org/abs/1105.3456