6.3: Van der Waals y Otros Gases

Hemos visto que los gases reales se asemejan a un gas ideal solo a bajas presiones y altas temperaturas. Se han realizado diversos intentos para encontrar una ecuación que represente adecuadamente la relación entre P, V y T para un gas real, es decir, encontrar una Ecuación de Estado para un gas real. Algunos de estos intentos han sido intentos puramente empíricos de ajustar una fórmula matemática a datos reales. Otros son el resultado de al menos un intento de describir algún modelo físico que explicara el comportamiento de los gases reales. A continuación se muestra una muestra de algunas de las ecuaciones más simples que se han propuesto:

Ecuación de van der Waals:

\[ \left( P + \frac{a}{V^2} \right) (V - b) = RT.\]

Ecuación de Berthelot:

\[ \left( R + \frac{a}{ \left( TV^2 \right)} \right) (V - b) = RT.\]

Ecuación de Clausi*:

\[ \left( P + \frac{a}{T(V+c)^2} \right) (V-b) = RT.\]

Ecuación de Dieterici:

\[ P (V-b)e^{ \frac{a}{(RTV)}} = RT.\]

Redlich-Kwong:

\[ P = \frac{RT}{V-b} - \frac{a}{bT^{ \frac{1}{2}}} \left( \frac{1}{V} - \frac{1}{V + b} \right).\]

Ecuación virial:

\[ PV = A +BP + CP^2 + DP^3 + ...\]

*En la ecuación de Clausius, si elegimos c = 3b, obtenemos un acuerdo bastante bueno entre el factor crítico de compresión de un gas Clausius y de muchos gases reales. El significado de “factor crítico de compresión”, y el cálculo de su valor para un gas Clausius se describe un poco más adelante en esta sección.

Hay muchas otras, pero con mucho la más conocida de ellas es la ecuación de van der Waals, que voy a describir con cierta extensión.

No es posible que la caja de voz de un hablante de inglés pronuncie correctamente el nombre van der Waals, aunque la W se pronuncia más como una V que una W, y, a mi oído, la v es algo intermedia entre una v y una f. Para escucharla correctamente pronunciada —especialmente las vocales − hay que preguntar a hablante nativo de holandés. La frecuente ortografía “ecuación de van der Waal” no es más que otro síntoma de la lamentable ignorancia moderna del uso del apóstrofo tanto lamentada por Lynne Truss.

Las unidades en las que deben expresarse las constantes a y b a veces causan dificultad, y dependen de si el símbolo V en la ecuación pretende significar el volumen específico o molar. Lo siguiente podría ser útil.

Si se pretende que V signifique el volumen específico, se debe escribir la ecuación de van der Waals\( \left( P + a/V^2 \right) (V-b) = RT/ \mu\), donde µ es la masa molar (“peso molecular”). En este caso las dimensiones y unidades SI de a son M ⁻¹ L ⁵ T ⁻² y Pa m ⁶ kg ⁻² y las dimensiones y unidades SI de b son M ⁻¹ L ³ y m ³ kg ⁻¹

Si se pretende que V signifique el volumen molar, la ecuación de van der Waals debe escribirse en su forma familiar\( \left( P + a/V^2 \right) (V-b) = RT\). En este caso las dimensiones y unidades SI de a son ML ⁵ T ⁻² mol ⁻² y Pa m ⁶ kmol ⁻² y las dimensiones y unidades SI de b son L ³ mol ⁻¹ y m ³ kmol ⁻¹

Las constantes de van der Waals, referidas al volumen molar, de H2O y CO2 son aproximadamente:

H ₂ O: a = 5.5 × 10 ⁵ Pa m ⁶ kmol ^−2. b = 3.1 × 10 ⁻² m ³ kmol ⁻¹

CO ₂: a = 3.7 × 10 ⁵ Pa m ⁶ kmol ⁻² b = 4.3 × 10 ⁻² m ³ kmol ⁻¹

La ecuación de van der Waals tiene su origen en al menos algún intento de describir un modelo físico de un gas real. Las propiedades de un gas ideal se pueden modelar suponiendo que un gas consiste en una colección de moléculas de tamaño efectivo cero y sin fuerzas entre ellas, y la presión es el resultado de colisiones con las paredes del recipiente contenedor. En el modelo de van der Waals, se supone que hay fuerzas atractivas entre las moléculas. Estas se conocen como fuerzas de van der Waals y ahora se entiende que surgen porque cuando una molécula se acerca a otra, cada una induce un momento dipolar en la otra, y los dos dipolos inducidos se atraen entonces entre sí. Esta fuerza de atracción reduce la presión en las paredes, siendo la reducción proporcional al número de moléculas en las paredes que están siendo atraídas por las moléculas debajo, y al número de moléculas debajo, que están haciendo la atracción. Ambos son inversamente proporcionales a V, por lo que la presión en la ecuación de estado tiene que ser reemplazada por la presión medida P más un término que es inversamente proporcional a V ². Además, las propias moléculas ocupan un volumen finito. Esto equivale a decir que, a muy corta distancia, hay fuerzas repulsivas (ahora entendidas como fuerzas de Coulomb) que son mayores que las atractivas fuerzas de van der Waals. Así, el volumen en el que las moléculas son libres para deambular tiene que ser reducido en la ecuación de van der Waals. Para más información sobre las fuerzas entre moléculas, véase la Sección 6.8.

Por convincentes o de otra manera que encuentres estos argumentos, son al menos un intento de describir alguna física, sí representan el comportamiento de los gases reales mejor que la ecuación de gas ideal, y, si nada más, nos dan una oportunidad para un poco de práctica matemática.

Veremos en breve cómo es posible determinar las constantes a y b a partir de mediciones de los parámetros críticos. Estas constantes a su vez nos dan alguna indicación de la fuerza de las fuerzas de van der Waals, y del tamaño de las moléculas.

La ecuación de Van der Waals, ecuación 6.3.1, puede escribirse

\[ P = \frac{RT}{V-b} - \frac{a}{V^2}.\]

Un punto de inflexión horizontal ocurre donde\( \frac{\partial P}{\partial V}\) y ambos\( \frac{\partial ^2 P}{\partial V^2}\) son cero. Eso es

\[ - \frac{RT}{(V-b)^2} + \frac{2a}{V^3} = 0\]

y

\[ \frac{2TR}{(V-b)^3} - \frac{6a}{V^4} = 0.\]

Elimine Rt/a de estos para encontrar el volumen molar crítico de un gas van der Waals:

\[ V_c = 3b.\]

Sustituya esto en la ecuación 6.3.8 o 6.3.9 (o ambas, como una comprobación de su álgebra) para obtener la temperatura crítica:

\[ T_c = \frac{8a}{27Rb}.\]

Sustituir las ecuaciones 6.3.10 y 6.3.11 en la ecuación 6.3.7 para obtener la presión crítica:

\[ P_c = \frac{a}{27b^2}.\]

A partir de estos, obtenemos fácilmente

\[ \frac{P_c V_c}{RT_c} = \frac{3}{8} = 0.375.\]

Esta cantidad suele denominarse factor crítico de compresión o factor crítico de compresibilidad, y la denotaremos con el símbolo Z _c. Para muchos gases reales Z _c es de aproximadamente 0.28; así la ecuación de van der Waals, si bien es útil para discutir las propiedades de los gases de manera cualitativa, no reproduce particularmente bien el factor de compresión crítico observado.

Ahora sustituyamos\( p = P/P_c,~ v = V/V_c,~ t = T/T_c,\) y la ecuación de van der Waals, en la que la presión, el volumen y la temperatura se expresan en términos de sus valores críticos, se convierte

\[ (p + 3/v^2)(v - \frac{1}{3} ) = \frac{8}{3} t.\]

Esto también se puede escribir

\[ 3pv^3 -(p+8t)v^2+9v-3 =0.\]

Para volúmenes menores a un tercio del volumen crítico, esta ecuación no describe en absoluto bien el comportamiento de un gas real. En efecto, se puede ver que p = ∞ cuando v = 1/3, lo que significa que hay que ejercer una presión infinita para comprimir un gas van der Waals a un tercio de su volumen crítico. Quizás quieras investigar por ti mismo el comportamiento de las ecuaciones 6.3.14 y 15 para volúmenes más pequeños que esto. Encontrarás que va al infinito en v = 0 y 1/3, y tiene un máximo entre estos dos volúmenes. Pero la ecuación es de interés físico sólo para v > 1/3, donde la variación de presión, volumen y temperatura lleva al menos alguna similitud con el comportamiento de los gases reales, si de ninguna manera es exacta. En la figura VI.2, muestro el comportamiento de un gas van der Waals para cinco temperaturas, una por encima de la temperatura crítica, otra a la temperatura crítica y tres por debajo de la temperatura crítica. El locus de máximos y mínimos se encuentra eliminando t entre la ecuación 6.3.14 y p /v = 0. Deberías probar esto, y mostrar que el locus de los máximos y mínimos (que he mostrado por una línea azul en la figura VI.2) viene dado por

\[ p = \frac{3}{v^2} - \frac{2}{v^3}\]

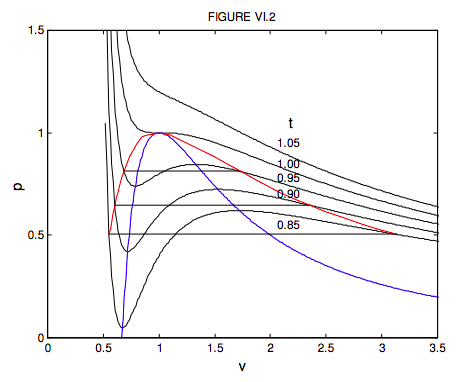
No confunda la curva azul en esta figura (muestra el locus de máximos y mínimos) con la curva discontinua en la figura VI.1 (muestra el límite entre fases). Para las temperaturas 0.85, 0.90 y 0.95 he dibujado las líneas de presión constante donde el líquido y el vapor están en equilibrio en el fluido real. Estos se dibujan para que dividan la curva van ver Waals en dos áreas iguales, arriba y abajo. Esto significa que el trabajo realizado por el fluido real cuando cambia de líquido a vapor a presión constante es igual al trabajo que realizaría su hipotético equivalente de van der Waals a lo largo de su trayectoria sinuosa. Posteriormente veremos que la colocación de la línea horizontal es consecuencia de que la función de Gibbs (que aún no hemos cumplido) es constante mientras el líquido y el vapor están en equilibrio. La línea discontinua de la figura VI.1 correspondería en la figura VI.2 al locus de los extremos de las líneas horizontales. He dibujado este locus, que perfila la región donde el líquido y el vapor están en equilibrio, en rojo en la figura VI.2. Si bien la ecuación de van der Waals es sólo una aproximación aproximada al comportamiento de los gases reales, sin embargo es cierto que, si las presiones, temperaturas y volúmenes molares se expresan en términos de las presiones críticas, temperaturas y volúmenes molares, las ecuaciones reales de estado de los gases reales son muy similares. Se dice que dos gases con los mismos valores de p, v y t están en los estados correspondientes, y la observación de que la relación p: v: t es aproximadamente la misma para todos los gases se denomina Ley de Estados Correspondientes. Podemos pensar en los gases como compuestos de partículas (moléculas) y la única diferencia entre diferentes gases está en los tamaños de sus moléculas (es decir, sus diferentes constantes van der Waals b) y sus momentos dipolares o sus polarizabilidades eléctricas (es decir, sus diferentes van der Waals a constantes). En las formas adimensionales de la ecuación de estado, estas constantes de van der Waals se eliminan de las ecuaciones, y no es sorprendente que todos los gases se ajusten entonces a la misma ecuación de estado.

Dejo al lector demostrar que, para un gas Berthelot, el volumen molar crítico, la temperatura y la presión y el factor crítico de compresión son, respectivamente, 3 b\( \sqrt{\frac{8 a}{27 b R}}\),\( \frac{1}{b} \sqrt{\frac{a R}{216 b}}\) y 0.375, que la ecuación de estado en términos de las variables adimensionales es

\[ p=\frac{8 t}{3 v-1}-\frac{3}{t v^{2}} ,\]

y que el locus de máximos y mínimos es

\[ p=\frac{1}{v^{1 / 2}}\left(\frac{4}{v}-\frac{6}{3 v-1}\right) .\]

Estos se muestran en la figura VI.2a. Se observará que el factor crítico de compresión es el mismo que (y por lo tanto no mejor que) para un gas van der Waals.

Para un gas Clausius, el volumen molar crítico, la temperatura y la presión y el factor crítico de compresión son, respectivamente, 3 b + 2 c,\( \sqrt{\frac{8 a}{27(b+c) R}}, \frac{1}{(b+c)} \sqrt{\frac{a R}{216(b+c)}}\) y\( \frac{3 b+2 c}{8(b+c)}\).

Si c = 3 b. estos se convierten en 3 c,\( \sqrt{\frac{2 a}{9 c R}}, \frac{1}{c} \sqrt{\frac{a R}{512 c}}\) y\( \frac{9}{32}=0.28125\). Elijo c = 3 b porque eso da un buen acuerdo con el factor crítico de compresión para muchos gases reales. En unidades adimensionales, la ecuación de Clausius se convierte

\[ p=\frac{32 t}{9 v-1}-\frac{48}{t(3 v+1)^{2}}\]

El locus de máximos y mínimos es

\[ p=\frac{1}{\sqrt{1+3 v}}\left(\frac{80-144 v}{1-6 v-27 v^{2}}\right)=\frac{16(5-9 v)}{(1-9 v)(1+3 v)^{3 / 2}}\]

Estos se muestran en la figura VI.2b

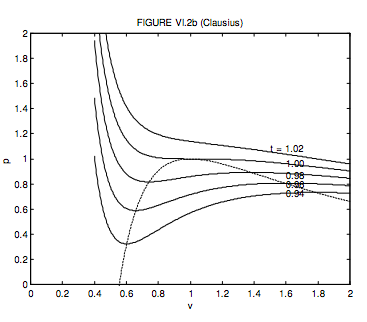
La ecuación de Clausius fue un trabajo duro. Dieteric's es un poco más fácil. El volumen molar crítico, la temperatura y la presión y el factor crítico de compresión son, respectivamente, 2 b,\( \frac{a}{4 R b}, \frac{a}{4 e^{2} b^{2}}\) y 2/ e ² = 0.271. Tenga en cuenta que el factor crítico de compresión es mucho más cercano al de muchos gases reales. La forma adimensional de la ecuación de Dieterici es

\[ p=\frac{t}{2 v-1} \exp \left(2-\frac{2}{t v}\right) .\]

El locus de máximos y mínimos es

\[ p=\frac{1}{v^{2}} \exp \left(\frac{2(v-1)}{2 v-1}\right) .\]

Estos se muestran en la figura VI.2c.

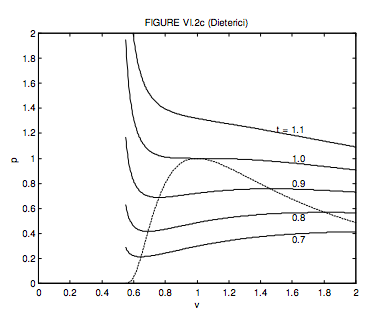
La ecuación de estado de Redlich-Kwong, como las de van der Waals, Bethelot y Dieterici, tiene apenas dos parámetros (a y b). Todos ellos no son tan malos a temperaturas apreciablemente superiores a la temperatura crítica, pero, cerca de la temperatura crítica, la ecuación empírica de Redlich-Kwong concuerda un poco mejor que la ecuación de van der Waals con lo que se observa para los gases reales. La obtención de las constantes críticas en términos de los parámetros se realiza exactamente por el mismo método que para la van der Waals y otras ecuaciones, pero requiere quizás un poco más de trabajo y paciencia. Al lector le puede gustar (o no gustarle) probarlo. Por las constantes críticas que obtengo

\[ V_{\mathrm{c}}=x b,\]

\[ T_{\mathrm{c}}=y\left(\frac{a}{b R}\right)^{2 / 3} \]

y

\[ P_{c}=z\left(\frac{a^{2} R}{b^{5}}\right)^{1 / 3} ,\]

donde

\[ x=3.847322100\]

\[ y=0.345039996\]

y

\[ z=0.029894386.\]

El factor crítico de compresión es xz/y, que es exactamente 1/3. Esto no es tan cercano al factor de compresión de muchos gases reales como lo es el factor de compresión crítico de Dieterici.

Podemos invertir estas ecuaciones para obtener expresiones para a y b en términos de la temperatura y presión críticas (o temperatura y volumen, o presión y volumen). Así

\[ a=u\left(\frac{R^{2} T_{c}^{5 / 2}}{P_{\mathrm{c}}}\right) \]

y

\[ b=w \frac{R T_{\mathrm{c}}}{P_{\mathrm{c}}} ,\]

donde

\[ u=0.427480233\]

y

\[ w=0.086640350. \]

(También se puede hacer esto para las otras ecuaciones de estado, claro.)

Para poder reproducir estos resultados, tendrás que hacer un poco de trabajo para ver de dónde provienen todas las constantes. Resulta que el valor de la constante x es la raíz real positiva de la ecuación

\[ x^{3}-3 x^{2}-3 x-1=0. \]

En el análisis anterior, obtuve todas las constantes de una solución numérica de la ecuación 6.3.33, pero la solución a esta ecuación (y todas las constantes posteriores) también se pueden escribir en surds. Así, con\( f=\sqrt[3]{2}-1, \quad g=\sqrt[3]{4}-1, \quad h=\sqrt[3]{16}-1 \), las constantes se pueden calcular a partir de

\[ x=\frac{1}{f}, \quad y=g^{2}, \quad z=\frac{3-5 g}{g+h}, \quad u=\frac{1}{9 f} \text { and } w=\frac{1}{3} f. \]

Si ahora introducimos las variables adimensionales\( p=P / P_{\mathrm{c}}, v=V N_{\mathrm{c}}, t=T / T_{\mathrm{c}}\), y sustituimos éstas y las ecuaciones 6.3.23-25 en la ecuación 6.3.6, obtenemos la ecuación adimensional de Redlich-Kwong

\[ p=\frac{l t}{x v-1}-\frac{1}{m t^{1 / 2}}\left(\frac{1}{x v}-\frac{1}{x v+1}\right) ,\]

donde

\[ l=y / z=11.54196631 \quad \text { and } \quad m=g z=0.017559994.\]

La ecuación adimensional de Redlich-Kwong se ilustra en la figura VI.2d. No he tratado de encontrar una ecuación explícita para el locus de máximos, sino que la calculé numéricamente, ilustrada por la línea discontinua en la figura VI.2d.

Aquí hay un resumen de los resultados para las ecuaciones de dos parámetros de estado:

\[ \begin{matrix} ~ & P_c & V_c & T_c & Z_c & a & b \\ \text{Van der Waals} & \frac{a}{27 b^{2}} & 3b & \frac{8 a}{27 R b} & \frac{3}{8} & \frac{27 R^{2} T_{\mathrm{c}}^{2}}{64 P_{\mathrm{c}}} & \frac{R T_{\mathrm{c}}}{8 P_{\mathrm{c}}} \\ \text{Berthelot} & \frac{1}{b} \sqrt{\frac{a R}{216 b}} & 3b & \sqrt{\frac{8 a}{27 b R}} & \frac{3}{8} & \frac{27 R^{2} T_{\mathrm{c}}^{3}}{64 P_{\mathrm{e}}} & \frac{R T_{\mathrm{c}}}{8 P_{\mathrm{c}}} \\ \text{Dieterici} & \frac{a}{4 e^{2} b^{2}} & 2b & \frac{a}{4 R b} & 2 e^{-2} & \frac{R T_{\mathrm{c}}}{e^{2} P_{\mathrm{c}}} & \frac{4 R^{2} T_{\mathrm{c}}^{2}}{e^{2} P_{\mathrm{c}}} \\ \text{Redlich-Kwong} & z\left(\frac{a^{2} R}{b^{5}}\right)^{1 / 3} & xb & y\left(\frac{a}{b R}\right)^{2 / 3} & \frac{1}{3} & u\left(\frac{R^{2} T_{c}^{5 / 2}}{P_{c}}\right) & w \frac{R T_{\mathrm{c}}}{P_{\mathrm{c}}} \\ ~ & z = 0.0299 & x = 3.85 & y = 0.345 & u = 0.427 & w = 0.0866 \end{matrix}\]

El lector puede intentar reproducir estos (avíseme ([e-mail]) si encuentra algún error!) o al menos (un ejercicio útil) verificar sus dimensiones. Mencionamos en la Sección 6.2 que una manera útil de indicar en qué se diferencia el comportamiento de un gas real del de un gas ideal es graficando el factor de compresión\( Z=\frac{P V}{R T}\) frente a la presión. A medida que la presión se acerca a cero, el factor de compresión se acerca a 1 Esto se debe a que las moléculas están entonces tan separadas que no hay fuerzas apreciables (atractivas o repulsivas) entre ellas. A medida que la presión se incrementa de cero, el factor de compresión generalmente al principio baja un poco por debajo de 1, y luego se eleva por encima de 1 a medida que aumenta la presión. Será interesante ver cómo se espera que el factor de compresión varíe con la presión para los diversos gases “teóricos” que hemos estado discutiendo. Lo haré solo por un gas van der Waals, y usaré la forma adimensional de la ecuación de van der Waals, que primero se dio como ecuación 6.3.14:

\[ \left(p+3 / v^{2}\right)\left(v-\frac{1}{3}\right)=\frac{8}{3} t.\]

El factor de compresión es\( Z=\frac{P V}{R T}\) y el factor crítico de compresión es\( Z_{c}=\frac{P_{c} V_{c}}{R T_{c}}\). A partir de esto, vemos eso\( Z=\frac{p v}{t} Z_{c}\). Para un gas van der Waals,\( Z_{c}=\frac{3}{8}\), así que\( Z=\frac{3 p v}{8 t}\). Desafortunadamente, para trazar Z versus p para una t dada, tenemos que ser capaces de expresar v en términos de p, lo que significa resolver la ecuación 6.3.37, que es una ecuación cúbica en\( v\left[3 p v^{3}-(p+8 t) v^{2}+9 v-3=0\right]\). Esto lo he hecho numéricamente, y muestro las gráficas resultantes de Z versus p para varias temperaturas, en la figura VI.2e. Observe que a p = 1 y t = 1, (es decir, en el punto crítico), el factor de compresión es 0.375. Las curvas Z versus p para gases reales tienen la misma forma general, pero el acuerdo preciso en detalle numérico no es tan bueno. Donde Z > 1, la presión es mayor que la de un gas ideal, siendo la parte b (repulsiva) de la ecuación de van der Waals más importante que la parte a (atractiva). Donde Z < 1, la presión es menor que la de un gas ideal, siendo la parte a (atractiva) de la ecuación de van der Waals más importante que la parte b (repulsiva). No he investigado si las otras ecuaciones “teóricas” de estado funcionan apreciablemente mejor. ¿Por qué no te vas tú mismo?

Figura VI.2e. El factor de compresión Z = PV/RT versus p (presión en unidades de la presión crítica para un gas van der Waals, para varios valores de t (temperatura en unidades de la temperatura crítica.) Para un gas van der Waals el factor de compresión es mayor a 1 para todas las temperaturas mayores a t = 27/8 = 3.375. A esta temperatura, el factor de compresión es cercano a 1 hasta p equivale aproximadamente a 2, y esta temperatura se conoce como la temperatura de Boyle. A la temperatura de Boyle, la curva Z: p es plana y cercana a 1 para un rango de presiones bastante grande. Así, a la temperatura de Boyle, incluso un gas no ideal obedece bastante de cerca la ley de Boyle. Para un gas van der Waals, la temperatura crítica es 8a/(27Rb), por lo que la temperatura de Boyle para un van der Waals es una/(Rb). El lector debe calcular esto para H ₂ O y CO ₂, utilizando los valores de las constantes de van der Waals dadas en este Capítulo. El punto en la isoterma t = 1.00 a p = 1 y Z = 0.375 corresponde al punto crítico. A cualquiera que se sienta necesitado de más ejercicio mental le gustaría preguntar: Por qué valor de p (distinto de cero) es Z = 1. Por ejemplo, ¿puede mostrar que, para t = 1, Z = 1 para p = 152/27 = 5.630?

La última ecuación empírica de estado propuesta que mencionamos es la ecuación virial, ecuación 6.3.6:\( P V=A+B P+C P^{2}+D P^{3}+\ldots \) Esto a veces se escribe en la forma\(P V=A+\frac{B}{V}+\frac{C}{V^{2}}+\frac{D}{V^{3}} \ldots \), pero en estas notas usaremos la forma de la ecuación 6.3.6. Los coeficientes A, B, etc se denominan los coeficientes viriales y son funciones de temperatura. El primer coeficiente, A, es solo RT. También podemos escribir la ecuación virial como

\[ Z=1+B^{\prime} P+C^{\prime} P^{2}+D^{\prime} P^{3}+\ldots \]

Podríamos medir el coeficiente B 'para un gas real trazando Z en función de la presión de manera similar a la figura VI.2e. La pendiente inicial\( \left(\frac{\partial Z}{\partial P}\right)_{T} \) extrapolada a presión cero da el valor de B '. A bajas temperaturas B 'es negativo; a altas temperaturas B' es positivo. A la temperatura de Boyle B 'es cero, y a esa temperatura el factor de compresión es la unidad para un amplio rango de presiones, y el gas en consecuencia se ajusta estrechamente a la ley de Boyle. El coeficiente C 'es pequeño, por lo que el término C' P ² entra en juego sólo a presiones más altas. A presiones más altas, Z aumenta, mostrando que C 'es un coeficiente positivo. El coeficiente D 'es aún menor que C'

Todas las ecuaciones matemáticamente “bien comportadas” de estado por debajo de la temperatura crítica tienen un máximo y un mínimo, es decir, la curva muestra un “meneo”. Esto lo ilustro en la figura VI.2f. Esta es la isoterma de van der Waals para t = 0.95 en variables adimensionales. Es lo mismo que una de las curvas que se muestran en la figura VI.2, dibujada a una escala diferente para enfatizar el “meneo”.

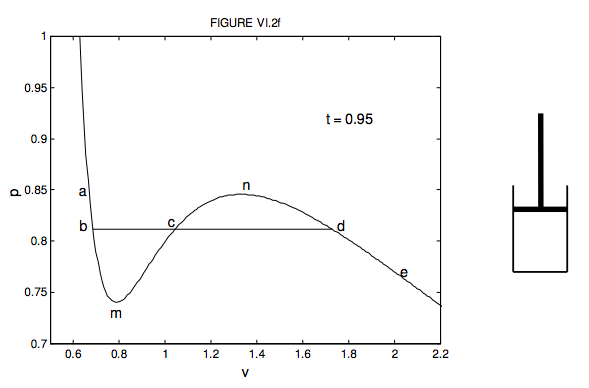
Usando el pequeño cilindro y el pistón a la derecha de la gráfica, intente imaginar lo que sucede con el líquido o vapor encerrado a medida que mueve el pistón hacia adentro y hacia afuera a temperatura constante, moviéndose de a a e y de nuevo en la gráfica. Empezar en e. El cilindro está lleno de vapor. Mueva el pistón hacia adentro, pasando de e a d; la presión aumenta y el volumen disminuye. Ahora un verdadero gas no sigue la función de van der Waals hasta el final. Al d, sucede algo diferente. En realidad es posible tomar un vapor un poco más allá de d hacia (pero no más allá) n. Eso sería un vapor superenfriado, tal como se usa en una cámara de nubes. Se condensará inmediatamente en una línea de gotitas de líquido tan pronto como una partícula cargada vuela a través del vapor. Sin embargo, lo que suele suceder es que parte del vapor comienza a condensarse como líquido, y nos movemos horizontalmente de d a b. A medida que bajamos el pistón a temperatura constante, el volumen por supuesto disminuye, y cada vez más líquido se condensa de tal manera que la presión permanece constante. En la porción db, tenemos líquido y vapor existentes juntos en el pistón, en equilibrio termodinámico. Cerca del extremo d solo hay un poco de líquido; cerca del extremo b es casi todo líquido, con solo un poco de vapor restante. Más allá de b, hacia a, el espacio está completamente lleno de líquido. Podemos empujar y empujar, aumentando la presión mucho, pero hay muy poco cambio en el volumen, porque el líquido es casi (aunque no del todo) incompresible. La isoterma es muy empinada ahí. En realidad es posible tomar el líquido un poco desde b hacia (pero no más allá) m sin que ninguno de ellos se vaporice. Este sería un líquido sobrecalentado, tal como se usa en una cámara de burbujas. Se vaporizará inmediatamente en una línea de burbujas tan pronto como una partícula cargada vuela a través del líquido.

Habrá más material importante referente al cambio de estado en los Capítulos 9 y 14. En la actualidad, sin embargo, quiero preguntar: ¿A qué presión comienza la condensación? Poniéndolo de otra manera, ¿cuál es la altura de la línea bd en la figura VI.2f? He escuchado argumentar que la altura de bd, (la presión a la que se produce la condensación) debe ser tal que el área bmc sea igual al área cnd. No estoy seguro de comprender completamente los argumentos que conducen a esta conclusión. Después de todo, un gas real no se ajusta exactamente a una ecuación de van der Waals ni a ninguna de las otras ecuaciones teóricas/empíricas que hemos discutido. Pero tal vez no sea irrazonable dibujar bd de tal manera que las áreas por encima y por debajo de ella sean iguales, y en cualquier caso lo convierte en un ejercicio computacional interesante (y desafiante). La ecuación de van der Waals, en variables adimensionales, se da como ecuación 6.3.14. ¿Se puede calcular la presión de tal manera que el área bmc por debajo de bd sea igual al área cnd por encima de ella? Lo hago p = 0.812, que es la altura donde la he dibujado en la figura. No he hecho el cálculo para las otras ecuaciones. ¡Te lo dejo a ti!