6.6: Colisiones

En esta sección, vamos a preguntar: ¿Cuál es el tiempo medio entre colisiones intermoleculares? ¿Cuál es el camino libre medio entre colisiones? ¿Cuántas colisiones intermoleculares hay por unidad de volumen por unidad de tiempo? ¿Cuántas colisiones con las paredes de una embarcación contenedora hay por unidad de área por unidad de tiempo? Como conozco poca química, asumiré que las moléculas son esferas duras de diámetro d. Esto puede no ser tan malo para los gases monatómicos como los gases raros. Para otros, la suposición equivale a suponer que las moléculas se repelen entre sí cuando sus centros de masa se acercan dentro de una distancia d. En todo caso, asumiremos que la sección transversal de colisión es de área π d ².

Observe, del boceto siguiente, que dos esferas iguales colisionan cuando sus centros están separados por su diámetro d, y en consecuencia la sección transversal de colisión (mostrada como un círculo discontinua) es de área π d ².

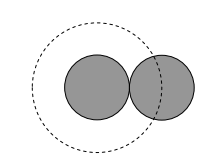
De hecho en lo que sigue, sólo voy a llamar al área de la colisión sección transversal σ; al hacer eso, ni siquiera tengo que asumir que su forma es circular.

En el tiempo t, una molécula que se mueve con velocidad c barre un cilindro de volumen σ ct. Si hay n moléculas por unidad de volumen, el número de colisiones que esa molécula en particular experimentará en el tiempo t parecería ser σ ctn, es decir que el número de colisiones que experimenta en el tiempo unitario es σ cn. Así, el tiempo medio τ entre colisiones parecería ser), τ = 1/ (σ cn) y la trayectoria libre media λ entre colisiones es). λ = 1/ (σ n).

Pero esto no está del todo bien, porque no hemos tomado en cuenta el hecho de que todas las moléculas del cilindro antes mencionado se están moviendo. No es como si nuestra molécula de héroe estuviera colisionando con un conjunto de moléculas estacionarias. La velocidad relevante a utilizar en este análisis es la velocidad relativa media entre moléculas, y esta es un poco mayor que la velocidad c de cada una. A ver si podemos hacerlo un poco mejor.

Comencemos suponiendo que todas las moléculas se mueven con la velocidad c. Hay dos tipos extremos de colisión:

La colisión “frontal”:

Para tal colisión, la velocidad relativa entre las moléculas es de 2 c.

Luego está el tipo de colisión en la que una molécula apenas alcanza a otra:

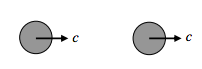
En ese caso la velocidad relativa es cero.

La velocidad relativa promedio está evidentemente en algún lugar entre 0 y 2 c.

Se trata de casos extremos. La situación “media” está algo intermedia. Podemos argumentar que la situación “promedio” es que las dos moléculas viajen en caminos perpendiculares:

Si pensamos en esto como la situación “promedio”, entonces podemos argumentar que la velocidad relativa “promedio” entre dos moléculas es\( \sqrt{2} c\). En ese caso, podemos concluir que el tiempo medio entre colisiones es\( \tau=1 /(\sqrt{2} \sigma c n)\), y el camino libre medio es\( \lambda=1 /(\sqrt{2} \sigma n)\).

Este argumento puede o no ser completamente convincente, pero probablemente esté más cerca de la marca que nuestro esfuerzo anterior.

A ver si podemos hacer una mejora adicional. Como antes, supondremos que cada molécula se mueve con velocidad c.

Supongamos que nuestra molécula héroe se mueve hacia arriba con la velocidad c, y otra molécula se acerca en un ángulo θ, como en el boceto a continuación.

Por adición vectorial de velocidades, se verá (se necesitará un poco de pensamiento) que es la velocidad relativa de aproximación entre las dos moléculas\( \sqrt{2} c(1+\cos \theta)^{1 / 2}\).

Ahora la fracción de moléculas que se aproximan desde ángulos entre θ y θ + d θ es\( \frac{1}{2} \sin \theta d \theta\). Esto se debe a que el área de una zona elemental de una esfera de radio unitario entre θ y θ + dθ es 2πsinθ d θ, y el área total de la esfera es 4π - vea el boceto a continuación:

Así es la velocidad relativa media de todas las moléculas\( \int_{0}^{\pi} \sqrt{2} c(1+\cos \theta)^{1 / 2} \times \frac{1}{2} \sin \theta d \theta \), que resulta ser\( \frac{4}{3} c\).

En este modelo, entonces, el tiempo medio entre colisiones sería\( \tau=\frac{1}{\frac{4}{3} \sigma c n}\), y el camino libre medio lo sería\( \lambda=\frac{1}{\frac{4}{3} \sigma n}\).

Sin embargo, todavía hemos asumido que todas las moléculas se mueven a la misma velocidad. Me han dicho (pero no lo he verificado yo mismo) que, si se toma en cuenta la distribución de velocidades Maxwell-Boltzmann (ver Sección 6.7), la velocidad relativa media de colisión es\( \sqrt{2} \overline{c}\), donde\( \overline{c}\) está la velocidad media de la distribución Maxwell-Boltzmann (igual a\( \sqrt{\frac{8 k T}{\pi m}}\).) Si eso es así, entonces obtenemos\( \tau=\frac{1}{\sqrt{2} \sigma \overline{c} n} \quad\) y\( \quad \lambda=\frac{1}{\sqrt{2} \sigma n}\).

En cualquier caso, dado que las moléculas no son esferas duras (no son esferas ni duras) y los detalles de una “colisión” dependen de la forma de las moléculas y de la ley de fuerza entre ellas, puede que no sea significativo tratar de obtener una fórmula extremadamente precisa para el camino libre medio, sino conformarse con \( \tau=\frac{1}{b \sigma \overline{c} n}\)y\( \lambda=\frac{1}{b \sigma n}\), y si quieres llevarte\( b \approx \sqrt{2}\), no estarás muy lejos.

De mayor interés sería calcular el tiempo medio entre colisiones para diversas presiones y temperaturas, y preguntar cómo se compara esto, por ejemplo, con la vida media de un átomo en un nivel atómico excitado, o un nivel metaestable. O comparar la trayectoria libre media entre colisiones con la distancia media del vecino más cercano entre moléculas en un gas. Creo que bajo condiciones familiares típicas, encontrarás que el camino libre medio es bastante más largo que la distancia media del vecino más cercano.

También es de interés el número de colisiones por unidad de volumen por unidad de tiempo. Si suponemos que una sola molécula experimenta\(b \sigma \overline{c} n\) colisiones por unidad de tiempo, y hay n moléculas por unidad de volumen, entonces el número de colisiones por unidad de volumen por unidad de tiempo es

\(Z=\frac{1}{2} b \sigma \overline{c} n^{2}\).

El factor de\( \frac{1}{2}\) es necesario para que no contemos colisiones de A con B y de B con A como dos colisiones diferentes.

Otro resultado útil es que el número de moléculas que golpean las paredes de un recipiente contenedor por unidad de área por unidad de tiempo es

\( \frac{1}{4} n \overline{c}\)

Para evitar repeticiones, no derivo esto aquí, pero encontrarás una derivación en el Capítulo 1 Sección 1.17 de Atmósferas Estelares, donde hago la derivación con fotones más que con moléculas. La única diferencia es que, en el caso de los fotones, todos se mueven a la misma velocidad c (la velocidad de la luz), mientras que aquí tenemos una distribución de velocidades, y usamos\(\overline{c}\), la velocidad media de las moléculas.