2.1: Descripción microscópica de un sistema clásico

Esta sección trata de la mecánica clásica, no de la mecánica estadística. Pero cualquier trabajo que intente construir conocimiento macroscópico a partir del conocimiento microscópico, como lo hace la mecánica estadística, debe comenzar con una declaración clara y precisa de lo que es ese conocimiento microscópico.

La descripción microscópica de un sistema físico tiene dos componentes: Primero, “¿Cuáles son las partes del sistema? ¿Cómo se afectan entre sí?” , segundo, “¿Cómo están dispuestas esas partes?”. La primera pregunta se responde dando los parámetros mecánicos ¹ del sistema. El segundo se responde dando sus variables dinámicas. En lugar de dar definiciones formales de estos términos, damos dos ejemplos.

El sistema tierra-luna. En este sistema, los parámetros mecánicos son la masa de la tierra, la masa de la luna, y (debido a que la tierra y la luna interactúan gravitacionalmente), la constante gravitacional G. Las variables dinámicas son la posición y velocidad (o impulso) de cada cuerpo. (Variables dinámicas alternativas son la posición del centro de masa y la separación entre los cuerpos, más el momento total del sistema y el momento angular de los dos cuerpos alrededor del centro de masa). Se puede ver a partir de este ejemplo que los parámetros mecánicos le dan el conocimiento para anotar el hamiltoniano para el sistema, mientras que las variables dinámicas son las cantidades que cambian según las leyes gobernadas por ese hamiltoniano. Los parámetros mecánicos no dependen de la condición inicial del sistema, las variables dinámicas sí. A menudo (aunque no siempre) los parámetros mecánicos son constantes de tiempo, mientras que las variables dinámicas varían en el tiempo.

Atomos de helio en una caja. Es natural comenzar la descripción diciendo que hay átomos de N, cada uno de masa m. Pero este comienzo inocente no es ni obvio ni precisamente correcto. Al decir que lo único que necesitamos saber de cada átomo es su masa, estamos modelando los átomos como partículas puntuales. Un modelo más preciso describiría el sistema como núcleos N y electrones 2N, pero entonces nuestro tratamiento necesariamente involucraría la mecánica cuántica en lugar de la mecánica clásica. Además, no ganaríamos nada con esta descripción más precisa y difícil... sabemos por experiencia que bajo condiciones ordinarias los núcleos y electrones sí se unen como átomos. Incluso la descripción más precisa no resultaría en un rigor inatacable, porque los núcleos mismos están formados por nucleones y los nucleones de quarks. De hecho, un proceso de construcción de modelos similar a éste continuó sin mencionar incluso en nuestro tratamiento del sistema tierra-luna: Cuando dijimos que necesitábamos conocer solo las masas de los dos cuerpos, estábamos asumiendo (una suposición buena pero no perfecta) que la distribución de la materia a través de la tierra y la luna era irrelevante a su moción. Adoptaremos el modelo que sustituye los átomos de helio por partículas puntuales, pero hay que tener en cuenta que se trata de un modelo.

Para continuar en nuestra descripción microscópica, necesitamos saber cómo interactúan los átomos entre sí. Un modelo común es que los átomos interactúan en pares a través de algún tipo de potencial de interacción átomo-átomo como el “potencial 6—12 de Lennard-Jones”:

\[\text { atom-atom potential energy }=-\frac{a}{r^{6}}+\frac{b}{r^{12}}. \label{2.1}\]

Aquí las cantidades\(a\) y\(b\) son parámetros mecánicos.

Una parte importante de la descripción microscópica de los átomos de helio en una caja es una descripción de la caja. Debemos saber dónde se encuentran las paredes y cómo interactúan las paredes con los átomos. Hay muchos modelos diferentes para la interacción pared-átomo: los modelos comunes incluyen las funciones de energía potencial de “pared dura” y “pared blanda” esbozadas en la figura\(\PageIndex{1}\). Pero incluso asumiendo que las paredes y los átomos interactúan a través de un potencial en absoluto estamos haciendo una suposición dramática y fácilmente pasada por alto: la suposición de una pared lisa, no atómica. Las paredes de caja reales están formadas en sí mismas por átomos, que por supuesto pueden moverse, por lo que no hay un punto fijo de “distancia cero” como lo implican las gráficas de la figura. El supuesto de paredes fijas y lisas implica que cuando un átomo choca con la pared su energía no cambia, mientras que es muy posible que el átomo gane o suelte algo de energía mientras choca con una pared atómica real. El supuesto de una pared lisa es particularmente sospechoso, y encontraremos en el capítulo 4 que se puede relajar de manera muy rentable.

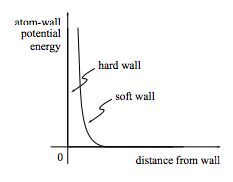
Figura\(\PageIndex{1}\)

El paso final es reconocer que puede haber campos externos eléctricos, magnéticos o gravitacionales que afecten al sistema. Si estos campos externos están presentes y relevantes deberán agregarse a la lista de parámetros mecánicos.

Por fin estamos listos para recurrir a las variables dinámicas para el sistema helio-atomos-in-a-box. Estos son (misericordiosamente) fáciles de describir: son solo la posición y el impulso de cada partícula, un total de 2 N vectores tridimensionales. Un nombre taquigráfico para esta información es “punto en el espacio de fase”. El espacio de fase es un espacio abstracto con una coordenada correspondiente a cada variable dinámica. Así, en nuestro ejemplo las coordenadas son las posiciones y momentos para la partícula número 1, número 2,.. número 9,.. y número N:

\[ \left(x_{1}, y_{1}, z_{1}, p_{x, 1}, p_{y, 1}, x_{2}, y_{2}, z_{2}, p_{z, 2}, \ldots x_{9}, y_{9}, z_{9}, p_{x, 9}, p_{y, 9}, \ldots x_{N}, y_{N}, z_{N}, p_{x, N}, p_{y, N}, p_{z, N}\right).\]

Para un sistema de partículas N, el espacio de fase es de 6 N -dimensional. Un solo punto en el espacio de fase da la posición y el impulso de cada partícula en el sistema.

¹ Los parámetros mecánicos a veces se denominan “parámetros en el hamiltoniano”, o “parámetros externos”, o “campos”.

Desarrollo temporal de un sistema clásico

Dada una descripción microscópica como cualquiera de las dos anteriores, ¿qué podemos hacer con ella? El desarrollo temporal del sistema está representado por el movimiento de un punto en el espacio de fase. Ese punto serpenteará a través de muchos puntos en el espacio de fase pero todos los puntos visitados tendrán la misma energía. ² Debido a que se visitarán muchos puntos de la energía dada, es natural preguntarse si, de hecho, todos los puntos de espacio de fase correspondientes a una energía dada eventualmente serán visitados por un sistema iniciado en alguno de esos puntos.

Es fácil encontrar sistemas para los que esta afirmación sea falsa, pero todos esos ejemplos parecen ser de una forma u otra atípicos. Por ejemplo, considere dos o tres o incluso muchos millones de partículas que no interactúan en una caja de paredes duras y comience a viajar todas hacia arriba y hacia abajo. Viajarán recto arriba y abajo para siempre. Los puntos en el espacio de fase con energía idéntica, pero con las partículas viajando de izquierda a derecha, nunca serán visitados. Este ejemplo es atípico porque si las partículas interactuaran, incluso ligeramente, entonces caerían de las regiones “rectas arriba y abajo” del espacio de fase.

Problemas

2.1 (Q) Interacciones de tres cuerpos: microscópicas

Informar un problema que involucre dos partículas de punto cargado y un átomo polarizable.

2.2 Parámetros mecánicos y variables dinámicas

Aquí hay un problema de la mecánica clásica: “Un péndulo bob de masa m se balancea al final de un cordón que atraviesa un pequeño agujero en el techo. El cordón está siendo jalado hacia arriba a través del agujero para que su longitud sea\(ell(t)=\ell_0 -\alpha t\). En el tiempo t = 0 el bob está en reposo y en ángulo\(\theta_0\). Encuentra el movimiento posterior del bob”. No resuelva este problema. En su lugar, enumere los parámetros mecánicos y las variables dinámicas que aparecen en él.

2.3 Un hamiltoniano

Anote el hamiltoniano total de un plasma neutro de N protones y N electrones moviéndose en una caja rectangular con dimensiones interiores de L _x × L _y × L _z, asumiendo que i) cualquier protón o electrón interactúa con el material de la pared a través de una función de energía potencial

\[W(d)=\left\{\begin{array}{cc}{W_{0}\left(\frac{1}{d^{2}}-\frac{1}{a^{2}}\right)} & {\text { for } d<a} \\ {0} & {\text { otherwise }}\end{array}\right.\]

donde d es la distancia (perpendicular) de la partícula en cuestión desde la pared, y ii) el sistema está sujeto a un campo eléctrico uniforme en la dirección ́x de magnitud E. Enumerar los parámetros mecánicos que aparecen en este hamiltoniano, y distinguirlos de las variables dinámicas.

2.4 (Q) Para discusión: Parámetros mecánicos, variables dinámicas y modelado

Enumerar los parámetros mecánicos y variables dinámicas de estos sistemas:

a. Moléculas de hidrógeno encerradas en una esfera.

b. Moléculas de agua en una caja.

c. Una mezcla de moléculas de hidrógeno y átomos de helio en una caja.

¿Hasta qué punto estás haciendo modelos a medida que generas descripciones? ¿Hasta qué punto estás haciendo suposiciones? (Por ejemplo, mediante el uso de la mecánica clásica no relativista.)

² Para el modelo tierra-luna, todos los puntos visitados también tendrán el mismo impulso total e impulso angular, pero este no es el caso del modelo de helio en una caja lisa.