2.11: Transiciones de fase y equilibrios de fase

Template:MathJaxArovas

Un diagrama de fases típico de un\(T\) sistema\(p\)\(V\) - - se muestra en la Fig. [pdiaga] (a). Las líneas continuas delimitan los límites entre distintas fases termodinámicas. Estas líneas se denominan curvas de convivencia. A lo largo de estas curvas, podemos tener coexistencia de dos fases, y los potenciales termodinámicos son singulares. El orden de la singularidad a menudo se toma como una clasificación de la transición de fase. si los potenciales termodinámicos\(E\),,\(F\)\(G\), y\(\CH\) tienen\(m^\ssr{th}\) derivados discontinuos o divergentes, se dice que la transición entre las fases respectivas es\(m^\ssr{th}\) orden. Las teorías modernas de las transiciones de fase generalmente solo reconocen dos posibilidades: transiciones de primer orden, donde el parámetro de orden cambia discontinuamente a través de la transición, y segundo orden transiciones, donde el parámetro de orden desaparece continuamente en el límite de fases ordenadas a desordenadas ¹². Discutiremos los parámetros de orden durante la Física 140B.

Para un diagrama de fases más interesante, ver Fig. [pdiaga] (b, c), que muestra los diagramas de fases para\({}^3\) Él y\({}^4\) Él. La única diferencia entre estos dos átomos es que el primero tiene un neutrón menos: (2p + 1n + 2e) en\({}^3\) He versus (2p + 2n + 2e) en\({}^4\) He. Como aprenderemos cuando estudiemos las estadísticas cuánticas, este neutrón extra marca toda la diferencia, porque\({}^3\) Él es un fermión mientras\({}^4\) que Él es un bosón.

[pdiaga] (a) Diagrama de fases termodinámico típico de un solo componente\(p\) -\(V\) -\(T\) sistema, mostrando punto triple (coexistencia trifásica) y punto crítico. (Fuente: Univ. de Helsinki.) También se muestran: diagramas de fases para\({}^3\) He (b) y\({}^4\) He (c). ¡Qué diferencia hace un neutrón! (Fuente: Brittanica.)

\(p\)-\(v\) -\(T\) superficies

La ecuación de estado para un sistema de un solo componente puede escribirse como\[f(p,v,T)=0\ .\] Esto puede, en principio, invertirse para ceder\(p=p(v,T)\) o\(v=v(T,p)\) o\(T=T(p,v)\). La restricción única\(f(p,v,T)\) en las tres variables de estado define una superficie en el\(\{p,v,T\}\) espacio. Un ejemplo de tal superficie se muestra en la Fig. [PVTiDeal], para el gas ideal.

Las\(T\) superficies reales\(p\) son mucho más ricas que las del gas ideal, ya que los sistemas reales experimentan transiciones de fase en las que las propiedades termodinámicas son singulares o discontinuas a lo largo de ciertas curvas en la\(p\)\(T\) superficie.\(v\)\(v\) Un ejemplo se muestra en la Fig. [PvTA]. Las isotermas de alta temperatura se asemejan a las del gas ideal, pero a medida que se enfría por debajo de la temperatura crítica\(T\ns_\Rc\), las isotermas se vuelven singulares. Precisamente en\(T=T\ns_\Rc\), la isoterma\(p=p(v,T\ns_\Rc)\) se vuelve perfectamente horizontal at\(v=v\ns_\Rc\), que es el volumen molar crítico. Esto significa que la compresibilidad isotérmica,\(\kappa\ns_T=-{1\over v}\big({\pz v\over\pz p}\big)\nd_T\) diverge en\(T=T\ns_\Rc\). A continuación\(T\ns_\Rc\), las isotermas tienen una porción plana, como se muestra en la Fig. [PvTb], correspondiente a una región bifásica donde coexisten líquido y vapor. En el\((p,T)\) plano, esbozado para\(\RH\ns_2\RO\) en la Fig. [H2Opd] y se muestra para\(\RC\RO\ns_2\) en la Fig. [PTCO2], esta coexistencia en fase líquido-vapor ocurre a lo largo de una curva, llamada curva de vaporización (o ebullición). La densidad cambia discontinuamente a través de esta curva; pues\(\RH\ns_2\RO\), el líquido es aproximadamente 1000 veces más denso que el vapor a presión atmosférica. La discontinuidad de densidad desaparece en el punto crítico. Tenga en cuenta que se puede transformar continuamente entre fases líquida y vapor, sin encontrar ninguna transición de fase, al rodear el punto crítico y evitar la región bifásica.

[PVTiDeal] La superficie\(p(v,T)=RT/v\) correspondiente a la ecuación de estado de gas ideal, y sus proyecciones sobre los\((T,v)\) planos\((p,T)\)\((p,v)\), y.

Además de la coexistencia líquido-vapor, también se produce la coexistencia sólido-líquido y sólido-vapor, como se muestra en la Fig. [PvTA]. El triple punto\((\RT\ns_\Rt, p\ns_\Rt)\) se encuentra en la confluencia de estas tres regiones de coexistencia. Para\(\RH\ns_2\RO\), la ubicación del punto triple y punto crítico viene dada por\[\begin{aligned} \RT\ns_\Rt &=273.16\,\RK & T\ns_\Rc&=647\,\RK\\ \Rp\ns_\Rt&=611.7\,{Pa}= 6.037\times 10^{-3}\,{atm} & \Rp\ns_\Rc&=22.06\,{MPa}=217.7\,{atm}\end{aligned}\]

[PvTa] A\(p\) -\(v\) -\(T\) superficie para una sustancia que se contrae al congelarse. El punto rojo es el punto crítico y la línea discontinua roja es la isoterma crítica. El punto amarillo es el punto triple en el que hay coexistencia trifásica de sólido, líquido y vapor.

La relación Clausius-Clapeyron

Recordemos que la homogeneidad de\(E(S,V,N)\) garantizado\(E=TS-pV+\mu N\), a partir del teorema de Euler. También garantiza una relación entre las variables intensivas\(T\),, y\(p\)\(\mu\), según la Ecuación [GdR]. Definamos\(g\equiv G/\nu=\NA\mu\), la energía libre de Gibbs por mol. Entonces\[dg=-s\,dT + v\,dp\ ,\] donde\(s=S/\nu\) y\(v=V/\nu\) están la entropía molar y el volumen molar, respectivamente. A lo largo de una curva de coexistencia entre la fase #1 y la fase #2\(g\ns_1=g\ns_2\), debemos tener, ya que las fases son libres de intercambiar energía y número de partículas, están en equilibrio térmico y químico. Esto significa\[dg\ns_1=-s\ns_1\,dT + v\ns_1\,dp = -s\ns_2\,dT + v\ns_2\,dp =dg\ns_2\ .\] Por lo tanto, a lo largo de la curva de coexistencia debemos tener\[\bigg({d p\over d T}\bigg)\ns_{coex}={s\ns_2-s\ns_1\over v\ns_2-v\ns_1}={\ell\over T\,\RDelta v}\ ,\] donde\[\ell\equiv T\,\RDelta s = T\,(s\ns_2-s\ns_1)\] está el calor molar latente de transición. Se\(\ell\) debe suministrar un calor para poder cambiar de la fase #1 a la fase #2, incluso sin cambiar\(p\) o\(T\). Si\(\ell\) es el calor latente por mol, entonces escribimos\({\tilde \ell}\) como el calor latente por gramo:\({\tilde \ell}=\ell/M\), donde\(M\) esta la masa molar.

[PvTc] Ecuación de estado para una sustancia que se expande al congelarse, proyectada a los\((T,p)\) planos\((v,T)\)\((v,p)\) y y.

A lo largo de la curva de coexistencia líquido-gas, normalmente tenemos\(v\ns_{gas}\gg v\ns_{liquid}\), y asumiendo que el vapor es ideal, podemos escribir\(\RDelta v\approx v\ns_{gas}\approx RT/p\). Así,\[\bigg({d p\over d T}\bigg)\ns_{liq-gas}={\ell\over T\,\RDelta v}\approx {p\,\ell\over R T^2}\ .\] si\(\ell\) permanece constante a lo largo de una sección de la curva de coexistencia líquido-gas, podemos integrar la ecuación anterior para obtener\[{dp\over p} = {\ell\over R}\,{dT\over T^2} \qquad\Longrightarrow\qquad p(T)=p(T\ns_0)\,e^{\ell/R T\ns_0}\,e^{-\ell/RT}\ .\]

Línea líquido-sólido en\(\RH_2\RO\)

La vida en el planeta tierra debe gran parte de su existencia a una propiedad peculiar del agua: el sólido es menos denso que el líquido a lo largo de la curva de convivencia. Por ejemplo at\(T=273.1\,\RK\) y\(p=1\,\) atm,\[{\tilde v}\ns_{water}=1.00013\,{cm}^3/\Rg \qquad,\qquad {\tilde v}\ns_{ice}=1.0907\,{cm}^3/\Rg\ .\] El calor latente de la transición es\({\tilde\ell}=333\,\RJ/\Rg = 79.5\,{cal}/\Rg\). Así, se invoca\[\begin{split} \bigg({d p\over d T}\bigg)\ns_{liq-sol}&=

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Fisica/Termodinámica_y_Mecánica_Estadística/Libro:_Termodinámica_y_Mecánica_Estadística_(Arovas)/02:_Termodinámica/2.11:_Transiciones_de_fase_y_equilibrios_de_fase), /content/body/div[3]/p[1]/span[5]/span, line 1, column 1

= {333\,\RJ/\Rg\over (273.1\,\RK)\,(-9.05\times 10^{-2}\,{cm}^3/\Rg)}\\ &=-1.35\times 10^{8}\,{{dyn}\over {cm}^2\,\RK} = -134\,{{atm}\over {}^\circ\RC}\ . \end{split}\] la pendiente negativa de la curva de fusión para explicar el movimiento de los glaciares: a medida que los glaciares se deslizan por una pendiente rocosa, generan una enorme presión en los obstáculos ¹³ Debido a esta presión, cuenta la historia, la temperatura de fusión disminuye, y el glaciar se derrite alrededor del obstáculo, para que pueda fluir más allá de él, después de lo cual se vuelve a congela. Pero no es el caso que el fondo del glaciar se derrita bajo la presión, por considerar un glaciar de altura\(h=1\,\) km. La presión en la parte inferior es\(p\sim gh/{\tilde v}\sim 10^7\,{Pa}\), que es de sólo unas 100 atmósferas. Tal presión puede producir solo un pequeño cambio en la temperatura de fusión de aproximadamente\(\RDelta T\ns_{melt}=-0.75^\circ\,\RC\).

[PvTb] Proyección de la\(T\) superficie\(p\)\(v\) - - de la Fig. [PvTa] en el\((v,p)\) avión.

¿La relación Clausius-Clapeyron explica cómo podemos patinar sobre hielo? Cuando mi hija tenía siete años, tenía una masa de aproximadamente\(M=20\,\) kg. Sus patines de hielo tenían cuchillas de ancho aproximadamente\(5\,\) mm y largo aproximadamente\(10\,\) cm. Así, incluso a un pie, impartió una presión adicional de solo\[\RDelta p={Mg\over A}\approx {20\,{kg}\times 9.8\,{\Rm/\Rs^2}\over (5\times 10^{-3}\,\Rm)\times (10^{-1}\,\Rm)} = 3.9\times 10^{5}\,{Pa}=3.9\,{atm}\ .\] El cambio correspondiente en la temperatura de fusión es así minúsculo:\(\RDelta T\ns_{melt}\approx -0.03^\circ\,\RC\).

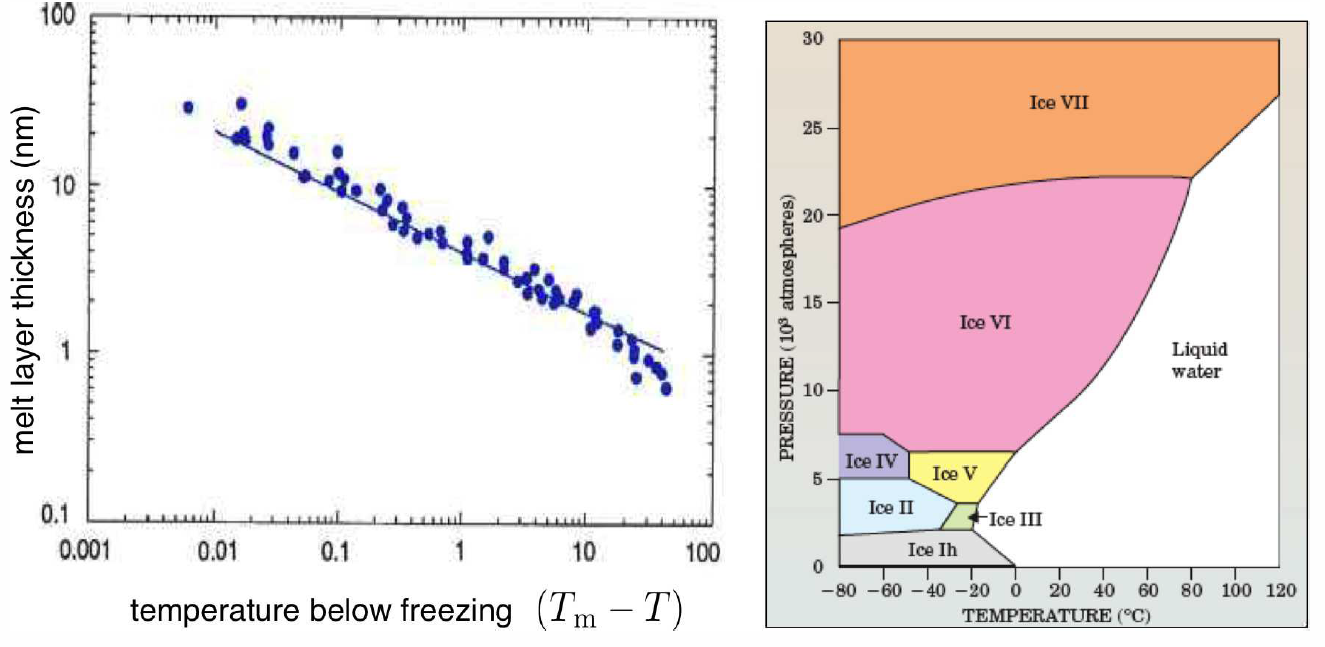
Entonces, ¿por qué mi hija podría patinar tan bien? ¡La respuesta no es tan clara! ¹⁴ Parece que hay dos temas relevantes en juego. Primero, la fricción genera calor que puede derretir localmente la superficie del hielo. Segundo, la superficie del hielo, y de muchos sólidos, es naturalmente resbaladiza. En efecto, este es el caso del hielo aunque uno esté parado, sin generar fuerzas de fricción. ¿Por qué es así? Resulta que la energía libre de Gibbs de la interfaz hielo-aire es mayor que la suma de energías libres de las interfaces hielo-agua y agua-aire. Es decir, el hielo, así como muchos sólidos simples, prefiere tener una fina capa de líquido en su superficie, incluso a temperaturas muy por debajo de su punto de fusión aparente. Si las interacciones intermoleculares no son de corto alcance ¹⁵, la teoría predice un espesor de fusión superficial\(d\propto (T\ns_\Rm-T)^{-1/3}\). En la Fig. [surfmelt] mostramos mediciones de Gilpin (1980) del derretimiento superficial sobre hielo, hasta aproximadamente\(-50^\circ\,\) C. Cerca\(0^\circ\,\RC\) del espesor de la capa de fusión es de aproximadamente\(40\,\) nm, pero esto disminuye a\(\sim 1\,\) nm a\(T=-35^\circ\,\) C. A temperaturas muy bajas, los patines se pegan en lugar de deslizarse. Por supuesto, el material del skate también es importante, ya que eso afectará la energética de la segunda interfaz. La novela del siglo XIX, Hans Brinker, o Los patines de plata de Mary Mapes Dodge cuenta la historia del pobre pero estereotípicamente decente y trabajador chico holandés Hans Brinker, que sueña con ganar una próxima carrera de patinaje sobre hielo, junto con el primer premio: un par de patines de plata. Todo lo que tiene son unos patines de madera pésimos, que no le servirán de nada en la carrera. Tiene dinero ahorrado para comprar patines de acero, pero claro que su padre necesita desesperadamente una operación porque —no me lo estoy inventando— se cayó de un dique y perdió la cabeza. La familia no tiene otra forma de pagar por el médico. ¡Qué historia! En este punto, imagino que el suspenso debe ser demasiado para que lo lleves, pero esta no es una clase de Literatura Americana, así que puedes usar Google para averiguar qué pasa (o rentar la película de 1958, dirigida por Sidney Lumet). Mi punto aquí es que los patines de madera de Hans no se pueden comparar con los metálicos, aunque la superficie se derrita entre el hielo y el aire es la misma. El material de la pala para patines también marca la diferencia, tanto por la energía de la interfaz como, quizás lo más importante, por la generación de fricción también.

Derretimiento lento del hielo: un proceso cuasistático pero irreversible

Supongamos que tenemos un cubito de hielo inicialmente a temperatura\(T\ns_0 < \Theta \equiv 273.15\,\RK\) (\(\Theta=0^\circ\,\RC\)) y lo arrojamos a un estanque de agua. Nosotros consideramos el estanque como un baño de calor a cierta temperatura\(T\ns_1>\Theta\). Que la masa del hielo sea\(M\). ¿Cuánto calor\(Q\) absorbe el hielo para elevar su temperatura a\(T\ns_1\)? Claramente\[Q=M {\tilde c}\ns_\ssr{S}(\Theta-T\ns_0) + M {\tilde \ell} + M{\tilde c}\ns_\ssr{L} (T\ns_1-\Theta)\ ,\] dónde\({\tilde c}\ns_\ssr{S}\) y\({\tilde c}\ns_\ssr{L}\) están los calores específicos de hielo (sólido) y agua (líquido), respectivamente ¹⁶, y\({\tilde\ell}\) es el calor latente de fusión por unidad de masa. El estanque debe ceder tanto calor al hielo, de ahí que la entropía del estanque, descontando el nuevo agua que vendrá del hielo derretido, debe disminuir:\[\RDelta S\ns_{pond}=-{Q\over T\ns_1}\ .\]

[PTCO2] Diagrama de fases para\(\RC\RO_2\) en el\((p,T)\) plano. (Fuente: www.scifun.org.)

Ahora nos preguntamos cuál es el cambio de entropía del\(\RH\ns_2\RO\) en el hielo. Tenemos\[\begin{split} \RDelta S\ns_{ice}&=\int\!{\dbar Q\over T} = \int\limits_{T\ns_0}^{\Theta}\!\!dT\,{M{\tilde c}\ns_\ssr{S}\over T} + {M{\tilde \ell}\over \Theta} + \int\limits_{\Theta}^{T\ns_1}\!\!dT\,{M{\tilde c}\ns_\ssr{L}\over T}\\ &=M{\tilde c}\ns_\ssr{S} \ln\!\bigg({\Theta\over T\ns_0}\bigg) + {M{\tilde\ell}\over \Theta} + M{\tilde c}\ns_\ssr{L} \ln\!\bigg({T\ns_1\over \Theta}\bigg) \ . \end{split}\] El cambio total de entropía del sistema es entonces\[\begin{split} \RDelta S\ns_{total}&=\RDelta S\ns_{pond} + \RDelta S\ns_{ice}\\ &=M{\tilde c}\ns_\ssr{S} \ln\!\bigg({\Theta\over T\ns_0}\bigg) - M{\tilde c}\ns_\ssr{S} \bigg({\Theta-T\ns_0\over T\ns_1}\bigg) + M{\tilde\ell}\,\bigg({1\over \Theta}-{1\over T\ns_1}\bigg) + M{\tilde c}\ns_\ssr{L} \ln\!\bigg({T\ns_1\over \Theta}\bigg) - M{\tilde c}\ns_\ssr{L}\bigg( {T\ns_1-\Theta\over T\ns_1}\bigg) \end{split}\] Ahora desde\(T\ns_0<\Theta <T\ns_1\), tenemos\[M{\tilde c}\ns_\ssr{S} \bigg({\Theta-T\ns_0\over T\ns_1}\bigg) < M{\tilde c}\ns_\ssr{S} \bigg({\Theta-T\ns_0\over \Theta}\bigg)\ .\] Por lo tanto,\[\RDelta S > M{\tilde\ell}\,\bigg({1\over \Theta}-{1\over T\ns_1}\bigg) + M{\tilde c}\ns_\ssr{S}\, f\big(T\ns_0/\Theta\big) + M{\tilde c}\ns_\ssr{L}\, f\big(\Theta/T\ns_1\big)\ ,\] dónde\(f(x)=x-1-\ln x\). Claramente\(f'(x)=1-x^{-1}\) es negativo en el intervalo\((0,1)\), lo que significa que el máximo de\(f(x)\) ocurre en\(x=0\) y el mínimo en\(x=1\). Pero\(f(0)=\infty\) y\(f(1)=0\), lo que significa que\(f(x)\ge 0\) para\(x\in [0,1]\). Ya que\(T\ns_0 < \Theta < T\ns_1\), concluimos\(\RDelta S\ns_{total} > 0\).

[surfmelt] Panel izquierdo: datos de R. R. Gilpin, J. Colloid Interface Sci. 77, 435 (1980) que muestra el espesor medido del derretimiento superficial sobre hielo a temperaturas por debajo de\(0^\circ\) C. La línea recta tiene pendiente\(-\frac{1}{3}\), como lo predice la teoría. Panel derecho: diagrama de fases de\(\RH_2\RO\), mostrando varias fases sólidas de alta presión. (Fuente: Physics Today, diciembre de 2005).

Regla de fase Gibbs

Equilibrio entre dos fases significa que\(p\),\(T\), y\(\mu(p,T)\) son idénticas. De\[\mu\ns_1(p,T)=\mu\ns_2(p,T)\ ,\] ahí derivamos una ecuación para la pendiente de la curva de coexistencia, la relación Clausius-Clapeyron. Tenga en cuenta que tenemos una ecuación en dos incógnitas\((T,p)\), por lo que el conjunto de soluciones es una curva. Para la coexistencia trifásica, tenemos\[\mu\ns_1(p,T)=\mu\ns_2(p,T)=\mu\ns_3(p,T)\ ,\] lo que nos da dos ecuaciones en dos incógnitas. La solución es entonces un punto (o un conjunto de puntos). Un punto crítico también es una solución de dos ecuaciones simultáneas:\[\hbox{critical point}\quad\Longrightarrow\quad v\ns_1(p,T)=v\ns_2(p,T) \quad,\quad \mu\ns_1(p,T)=\mu\ns_2(p,T)\ .\] Recall\(v=\NA\big({\pz\mu\over\pz p}\big)\ns_T\). Tenga en cuenta que no puede haber coexistencia de cuatro fases para un\(T\) sistema simple\(p\).\(V\)

Ahora para el resultado general. Supongamos que tenemos\(\sigma\) especies, con números de partículas\(N\ns_a\), donde\(a=1,\ldots,\sigma\). Es útil recapitular brevemente la derivación de la relación Gibbs-Duhem. La energía\(E(S,V,N\ns_1,\ldots,N\ns_\sigma)\) es una función homogénea del grado uno:\[E(\lambda S,\lambda V,\lambda N\ns_1,\ldots,\lambda N\ns_\sigma)=\lambda E(S,V,N\ns_1,\ldots,N\ns_\sigma)\ .\] Del teorema de Euler para funciones homogéneas (solo diferenciar con respecto\(\lambda\) y luego establecer\(\lambda=1\)), tenemos\[E=TS-p\,V+\sum_{a=1}^\sigma \mu\ns_a\, N\ns_a\ .\] Tomando el diferencial, e invocando la Primera Ley,\[dE=T\,dS - p\,dV + \sum_{a=1}^\sigma \mu\ns_a \,dN\ns_a\ ,\] llegamos a la relación \[S\,dT - V dp + \sum_{a=1}^\sigma N\ns_a\,d\mu\ns_a =0\ ,\]de los cuales la Ecuación [RDA] es una generalización a variables adicionales de 'trabajo' internas. Esto dice que las\(\sigma+2\) cantidades no\((T,p,\mu\ns_1,\ldots,\mu\ns_\sigma)\) son todas independientes. Por lo tanto, podemos escribir\[\mu\ns_\sigma=\mu\ns_\sigma\big(T,p,\mu\ns_1,\ldots,\mu\ns_{\sigma-1}\big)\ .\]

Si hay\(\varphi\) diferentes fases, entonces en cada fase\(j\), con\(j=1,\ldots,\varphi\), hay un potencial químico\(\mu^{(j)}_a\) para cada especie\(a\). Entonces tenemos\[\mu^{(j)}_\sigma=\mu^{(j)}_\sigma\Big(T,p,\mu^{(j)}_1,\ldots,\mu^{(j)}_{\sigma-1}\Big)\ .\] Aquí\(\mu_a^{(j)}\) está el potencial químico de la\(a^\ssr{th}\) especie en la\(j^\ssr{th}\) fase. Así, existen\(\varphi\) tales ecuaciones que relacionan las\(2+\varphi\,\sigma\) variables\(\big(T,p,\big\{\mu^{(j)}_a\big\}\big)\), lo que significa que solo\(2+\varphi\,(\sigma-1)\) de ellas pueden elegirse como independientes. Esta, entonces, es la dimensión del 'espacio termodinámico' que contiene un número máximo de variables intensivas:\[d\ns_\ssr{TD}(\sigma,\varphi)=2+\varphi\,(\sigma-1)\ .\] Para especificar completamente el estado de nuestro sistema, por supuesto introducimos una sola variable extensa, como el volumen total\(V\). ¡Tenga en cuenta que el número total de partículas\(N=\sum_{a=1}^\sigma N\ns_a\) puede no conservarse en presencia de reacciones químicas!

Ahora supongamos que tenemos equilibrio entre\(\varphi\) fases. Hemos asumido implícitamente el equilibrio térmico y mecánico entre todas las fases, lo que significa que\(p\) y\(T\) son constantes. El equilibrio químico se aplica especie por especie. Esto significa\[\mu_a^{(j)}=\mu_a^{(j')} \label{phaseq}\] dónde\(j,j'\in\{1,\ldots,\varphi\}\). Esto da ecuaciones\(\sigma(\varphi-1)\) independientes ecuaciones ¹⁷. Así, podemos tener equilibrio de fases entre las\(\varphi\) fases de las\(\sigma\) especies sobre una región de dimensión\[\begin{split} d\ns_\ssr{PE}(\sigma,\varphi)&=2+\varphi\,(\sigma-1)-\sigma\,(\varphi-1)\\ &=2+\sigma-\varphi\ . \end{split}\] Desde\(d_\ssr{PE}\ge 0\), debemos tener\(\varphi\le \sigma+2\). Así, con dos especies (\(\sigma=2\)), podríamos tener como máximo cuatro fases de coexistencia.

Si las diversas especies pueden sufrir\(\rho\) distintas reacciones químicas de la forma\[\zeta^{(r)}_1\,\RA\ns_1 + \zeta^{(r)}_2\,\RA\ns_2 + \cdots + \zeta^{(r)}_\sigma\,\RA\ns_\sigma=0\ ,\] donde\(\RA\ns_a\) está la fórmula química para las especies\(a\), y\(\zeta^{(r)}_a\) es el coeficiente estequiométrico para las\(a^\ssr{th}\) especies en la\(r^\ssr{th}\) reacción\(r=1,\ldots,\rho\), con, entonces tenemos un \(\rho\)restricciones adicionales de la forma\[\sum_{a=1}^\sigma\zeta^{(r)}_a\,\mu^{(j)}_a=0\ . \label{reacon}\] Por lo tanto,\[d\ns_\ssr{PE}(\sigma,\varphi,\rho)=2+\sigma-\varphi-\rho\ .\] Uno podría preguntarse qué valor de\(j\) vamos a utilizar en la Ecuación\ ref {reacon}, o de hecho tenemos\(\varphi\) tales ecuaciones para cada una\(r\)? La respuesta es que la Ecuación [phaseq] garantiza que el potencial químico de las especies\(a\) es el mismo en todas las fases, de ahí que no importa qué valor se elija\(j\) en la Ecuación [reacón].

Supongamos que no se producen reacciones\(\rho=0\), por lo que\(\sum_{b=1}^\sigma N\ns_b\) se conserva el número total de partículas. En lugar de elegir\((T,p,\mu\ns_1,\ldots,\mu^{(j)}_{\sigma-1})\) como variables\(d\ns_\ssr{TD}\) intensivas, podríamos haber elegido\((T,p,\mu\ns_1,\ldots,x^{(j)}_{\sigma-1})\), dónde\(x\ns_a=N\ns_a/N\) está la concentración de especies\(a\).

¿Por qué los diagramas de fase en el\((T,v)\) plano\((p,v)\) y se ven diferentes a los del\((p,T)\) plano? ¹⁸ Por ejemplo, la Fig. [PvTc] muestra proyecciones de la\(T\) superficie\(p\)\(v\) - - de una sustancia típica de un solo componente en los\((p,T)\) planos\((T,v)\)\((p,v)\), y. La coexistencia tiene lugar a lo largo de curvas en el\((p,T)\) plano, pero en regiones bidimensionales extendidas en los\((p,v)\) planos\((T,v)\) y. La razón por la que\(p\) y\(T\) son especiales es que la temperatura, la presión y el potencial químico deben ser iguales a lo largo de una fase de equilibrio si realmente está en equilibrio térmico, mecánico y químico. Este no es el caso de una variable intensiva como el volumen específico\(v=\NA V/N\) o la concentración química\(x\ns_a=N\ns_a/N\).