2.12: La entropía de la mezcla y la paradoja de Gibbs

Template:MathJaxArovas

Computación de la entropía de la mezcla

La entropía es ampliamente entendida como una medida del trastorno. Por supuesto, tal definición debería complementarse con una definición más precisa de desorden —después de todo, la basura de un hombre es el tesoro de otro hombre. Para obtener cierta intuición sobre la entropía, exploremos la mezcla de un gas ideal multicomponente. Dejar\(N=\sum_a N\ns_a\) ser el número total de partículas de todas las especies, y dejar\(x\ns_a=N\ns_a/N\) ser la concentración de especies\(a\). Tenga en cuenta que\(\sum_a x\ns_a=1\).

Para cualquier sustancia que obedezca a la ley de gas ideal\(pV=N\kT\), la entropía es\[S(T,V,N)=N\kB\ln(V/N)+ N\phi(T)\ , \label{STVNideal}\] desde entonces\(\big({\pz S\over\pz V}\big)\ns_\sss{T,N}=\big({\pz p\over\pz T}\big)\ns_\sss{V,N}={N\kB\over V}\). Tenga en cuenta que en la Ecuación [StvNideAL] hemos dividido\(V\) por\(N\) antes de tomar el logaritmo. Esto es esencial si la entropía va a ser una función extensa (ver § 7.5). Se podría pensar que la entropía configuracional de un gas ideal debería escalar como\(\ln(V^N)=N\ln V\), ya que cada partícula puede estar en cualquier parte del volumen\(V\). Sin embargo, si las partículas son indistinguibles, entonces permutar las etiquetas de partículas no da como resultado una configuración distinta, por lo que la entropía configuracional es proporcional a\(\ln(V^N/N!)\sim N\ln(V/N)-N\). El origen de este factor de indistinguibilidad quedará claro cuando se discuta la formulación mecánica cuántica de la mecánica estadística. Por ahora, tenga en cuenta que tal corrección es necesaria para que la entropía sea una función extensa.

Si no incluimos este factor y en cambio escribimos\(S^*(T,V,N)=N\kB\ln V + N\phi(T)\), entonces encontraríamos\(S^*(T,V,N)-2S^*(T,\half V,\half N)=N\kB\ln 2\), la entropía total de dos sistemas idénticos de partículas separadas por una barrera aumentará si se elimina la barrera y se les permite mezclarse. Esto parece absurdo, sin embargo, porque bien podríamos considerar las barreras como invisibles. Esto se conoce como la paradoja de Gibbs. La resolución de la paradoja de Gibbs es incluir la corrección de indistinguibilidad, que hace\(S\) extensiva, en cuyo caso\(S(T,V,N)=2S(T,\half V,\half N)\).

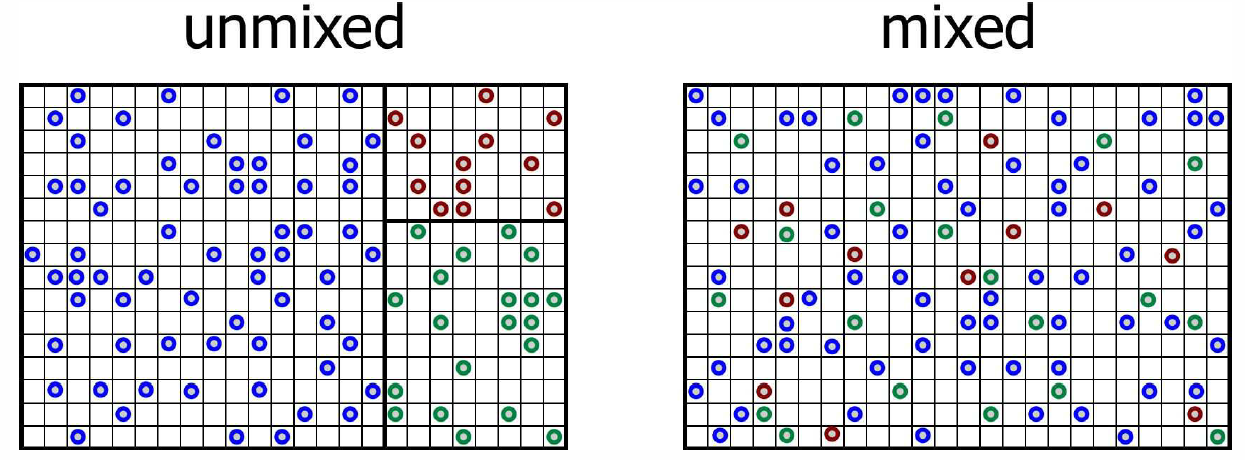
Consideremos ahora la situación en la Fig. [cajas], donde hemos separado los diferentes componentes en sus propios volúmenes\(V\ns_a\). Que la presión y la temperatura sean las mismas en todas partes, así que\(p V\ns_a = N\ns_a\kT\). La entropía del sistema no mezclado es entonces\[S\ns_{unmixed}=\sum_a S\ns_a=\sum_a \Big[N\ns_a\,\kB\ln(V\ns_a/N\ns_a) + N\ns_a\,\phi\ns_a(T)\Big]\ .\]

[cajas] Un sistema multicomponente que consiste en gases aislados, cada uno a temperatura\(T\) y presión\(p\). Entonces la entropía del sistema aumenta cuando se eliminan todas las paredes entre los diferentes subsistemas.

Ahora imaginemos eliminar todas las barreras que separan los diferentes gases y dejar que las partículas se mezclen a fondo. El resultado es que cada gas componente ocupa el volumen completo\(V\), por lo que la entropía es\[S\ns_{mixed}=\sum_a S\ns_a=\sum_a \Big[N\ns_a\,\kB\ln(V/ N\ns_a) + N\ns_a\,\phi\ns_a(T)\Big]\ .\] así, la entropía de mezcla es\[\begin{split} \RDelta S\ns_{mix} &= S\ns_{mixed} - S\ns_{unmixed}\\ &= \sum_a N\ns_a\,\kB\,\ln(V/ V\ns_a) =-N\kB\sum_a x\ns_a\ln x\ns_a\ , \end{split}\] donde\(x\ns_a=\frac{N_a}{N}=\frac{V_a}{V}\) está la fracción de especies\(a\). Tenga en cuenta que\(\RDelta S\ns_{mix}\ge 0\).

¿Y si todos los componentes fueran inicialmente idénticos? Parece absurdo que la entropía se incremente simplemente quitando algunas barreras invisibles. Esta es nuevamente la paradoja de Gibbs. En este caso, la resolución de la paradoja es señalar que la suma en la expresión for\(S\ns_{mixed}\) es una suma sobre especies distintas. De ahí que si las partículas son todas idénticas, tenemos\(S\ns_{mixed}=N\kB\ln(V/N)+N\phi(T) = S\ns_{unmixed}\), de ahí\(\RDelta S\ns_{mix}=0\).

Entropía y combinatoria

Como aprenderemos cuando estudiemos la mecánica estadística, la entropía puede interpretarse en términos de la cantidad de formas en que\(W(E,V,N)\) un sistema a energía fija y volumen puede organizarse. Uno tiene\[S(E,V,N)=\kB\ln W(E,V,N)\ .\] Considerar un sistema que consiste en\(\sigma\) diferentes especies de partículas. Ahora que sea que para cada etiqueta de especie\(a\),\(N\ns_a\) las partículas de esa especie están confinadas entre\(Q\ns_a\) cajitas de tal manera que a lo sumo una partícula puede caber en una caja (ver Fig. [Smix]). ¿Cuántas formas\(W\) hay de configurar partículas\(N\) idénticas entre\(Q\) cajas? Claramente, si las partículas\[W={Q\choose N}={Q!\over N! \, (Q-N)!}\ .\] fueran distintas, las tendríamos\(W\ns_{distinct}={Q!\over(Q-N)!}\), que es\(N!\) veces mayor. Esto se debe a que permutar partículas distintas resulta en una configuración diferente, y hay\(N!\) formas de permutar\(N\) partículas.

La entropía para las especies\(a\) es entonces\(S\ns_a=\kB\ln W\ns_a=\kB\ln\!\Big({Q\ns_a\atop N\ns_a}\Big)\). Luego usamos la aproximación de Stirling,\[\ln(K!) = K\ln K - K + \half\ln K + \half\ln(2\pi) + \CO(K^{-1})\ ,\] que es una expansión asintótica válida para\(K\gg 1\). Uno luego encuentra para\(Q,N\gg 1\), con\(x=N/Q\in [0,1]\),\[\begin{aligned} \ln {Q\choose N} &= \Big( Q\ln Q - Q \Big) - \Big(xQ\ln(xQ)-xQ\Big) - \Big((1-x)Q\ln\big((1-x)Q\big)-(1-x)Q\Big) \nonumber \\ &=-Q\Big[x\ln x + (1-x)\ln(1-x)\Big]\ .\end{aligned}\] Esto es válido hasta términos de orden\(Q\) en la expansión de Stirling. Ya que\(\ln Q \ll Q\), el próximo término es pequeño y estamos seguros de parar aquí. Resumiendo los aportes de todas las especies, obtenemos\[S\ns_{unmixed} = \kB\sum_{a=1}^\sigma\ln W\ns_a = - \kB\sum_{a=1}^\sigma Q\ns_a \Big[x\ns_a\ln x\ns_a + (1-x\ns_a)\ln(1-x\ns_a)\Big]\ ,\] dónde\(x\ns_a=N\ns_a/Q\ns_a\) está la densidad adimensional inicial de especies\(a\).

[Smix] Mezcla entre tres especies diferentes de partículas. La configuración mixta tiene una entropía adicional,\(\RDelta S_{mix}\).

Ahora vamos a eliminar todas las particiones entre las diferentes especies para que cada una de las partículas sea libre de explorar todas las cajas. Hay\(Q=\sum_a Q\ns_a\) cajas en todos. El número total de formas de colocar\(N\ns_1\) partículas de especies\(a=1\) a través de\(N\ns_\sigma\) partículas de especies\(\sigma\)\(N\ns_0=Q-\sum_{a=1}^\sigma N\ns_a\) es\[W\ns_{mixed}={Q!\over N\ns_0! \, N\ns_1! \cdots N\ns_\sigma!}\ ,\] donde está el número de cajas vacías. Nuevamente usando la regla de Stirling, encontramos\[S\ns_{mixed}=-\kB\,Q \sum_{a=0}^\sigma {\widetilde x}\ns_a \ln {\widetilde x}\ns_a\ ,\] dónde\({\widetilde x}\ns_a=N\ns_a/Q\) está la fracción de todas las cajas que contienen una partícula de especies\(a\), y\(N\ns_0\) es el número de cajas vacías. Tenga en cuenta que\[{\widetilde x}\ns_a={N\ns_a\over Q}={N\ns_a\over Q\ns_a}\cdot{Q\ns_a\over Q}=x\ns_a \, f\ns_a\ ,\] donde\(f\ns_a\equiv Q\ns_a/Q\). Tenga en cuenta que\(\sum_{a=1}^\sigma f\ns_a=1\).

Supongamos que todas las densidades son inicialmente las mismas, entonces\(x\ns_a=x\forall a\), así\({\widetilde x}\ns_a=x\,f\ns_a\). En este caso,\(f\ns_a={Q\ns_a\over Q}={N\ns_a\over N}\) es la fracción de especies\(a\) entre todas las partículas. Entonces tenemos\({\widetilde x}\ns_0=1-x\), y\[\begin{split} S\ns_{mixed}&=-\kB\, Q\sum_{a=1}^\sigma x f\ns_a\ln (x f\ns_a) - \kB \,Q\,{\widetilde x}\ns_0\ln{\widetilde x}\ns_0\\ &=-\kB \,Q \Big[x\ln x + (1-x)\ln(1-x)\Big] - \kB\,x\,Q\sum_{a=1}^\sigma f\ns_a\ln f\ns_a\ . \end{split}\] así, la entropía de mezcla es\[\RDelta S\ns_{mix}=-N\kB\sum_{a=1}^\sigma f\ns_a\ln f\ns_a \ ,\] donde\(N=\sum_{a=1}^\sigma N\ns_a\) está el número total de partículas entre todas las especies (excluyendo vacantes) y\(f\ns_a=N\ns_a/(N+N\ns_0)\) es la fracción de todas las cajas ocupadas por especies\(a\).

Soluciones débiles y presión osmótica

Supongamos que una de las especies es mucho más abundante que todas las demás, y etiquetarla con\(a=0\). A esto lo llamaremos el solvente. La entropía de la mezcla es entonces\[\RDelta S\ns_{mix}=-\kB\Bigg[N\ns_0\ln\!\bigg({N\ns_0\over N\ns_0+N'}\bigg) + \sum_{a=1}^\sigma N\ns_a\ln\!\bigg({N\ns_a\over N\ns_0+N'}\bigg)\Bigg]\ ,\] donde\(N'=\sum_{a=1}^\sigma N\ns_a\) está el número total de moléculas de disolvente, sumadas sobre todas las especies. Asumimos que la solución es débil, lo que significa\(N\ns_a\le N'\ll N\ns_0\). Ampliando en poderes de\(N'/N\ns_0\) y\(N\ns_a/N\ns_0\), encontramos\[\RDelta S\ns_{mix}=-\kB\sum_{a=1}^\sigma\Bigg[N\ns_a\ln\!\bigg({N\ns_a\over N\ns_0}\bigg) -N\ns_a\Bigg] + \CO\big({N'}^2/N\ns_0\big)\ . \label{smixweak}\]

Consideremos ahora una solución que consiste en\(N\ns_0\) moléculas de un disolvente y\(N\ns_a\) moléculas de especies\(a\) de soluto, donde\(a=1,\ldots,\sigma\). Comenzamos por expandir la energía libre de Gibbs\(G(T,p,N\ns_0,N\ns_1,\ldots,N\ns_\sigma)\), donde hay\(\sigma\) especies de solutos, como una serie de potencia en las pequeñas cantidades\(N\ns_a\). Tenemos\[\begin{split} G\big(T,p,N\ns_0,\{N\ns_a\}\big)&=N\ns_0\, g\ns_0(T,p) + \kT\sum_a N\ns_a \ln\!\bigg({N\ns_a\over e N\ns_0}\bigg)\\ &\qquad\qquad + \sum_a N\ns_a\,\psi\ns_a(T,p) + {1\over 2N\ns_0}\sum_{a,b} A\ns_{ab}(T,p)\,N\ns_a \,N\ns_b\ . \end{split}\] El primer término en el RHS corresponde a la energía libre de Gibbs del solvente. El segundo término se debe a la entropía de la mezcla. El tercer término es la contribución a la energía libre total de las especies individuales. Anote el factor de\(e\) en el denominador dentro del logaritmo, que representa el segundo término entre paréntesis en el RHS de la ecuación\ ref {smixweak}. El último término se debe a las interacciones entre las especies; se trunca en segundo orden en los números de solutos.

El potencial químico para el solvente es\[\mu\ns_0(T,p)={\pz G\over\pz N\ns_0}= g\ns_0(T,p) - \kT\sum_a x\ns_a -\half\sum_{a,b} A\ns_{ab}(T,p)\,x\ns_a\, x\ns_b\ ,\] y el potencial químico para las especies\(a\)\(x\ns_a=N\ns_a/N\ns_0\) es\[\mu\ns_a(T,p)={\pz G\over\pz N\ns_a}=\kT\ln x\ns_a + \psi\ns_a(T,p) + \sum_b A\ns_{ab}(T,p)\,x\ns_b\ ,\] donde están las concentraciones de especies de soluto\(a\). Por suposición, el último término sobre el RHS de cada una de estas ecuaciones es pequeño, ya que\(N\ns_{solute}\ll N\ns_0\), donde\(N\ns_{solute}=\sum_{a=1}^\sigma N\ns_a\) está el número total de moléculas de soluto. Al orden más bajo, entonces, tenemos\[\begin{aligned} \mu\ns_0(T,p)&= g\ns_0(T,p) - x\,\kT\\ \mu\ns_a(T,p)&=\kT\ln x\ns_a + \psi\ns_a(T,p) \ ,\end{aligned}\] donde\(x=\sum_a x\ns_a\) está la concentración total de soluto.

[osmótica] La presión osmótica hace que la columna del lado derecho del tubo en U se eleve más alta que la columna de la izquierda en una cantidad\(\RDelta h=\pi/\vrh\,g\).

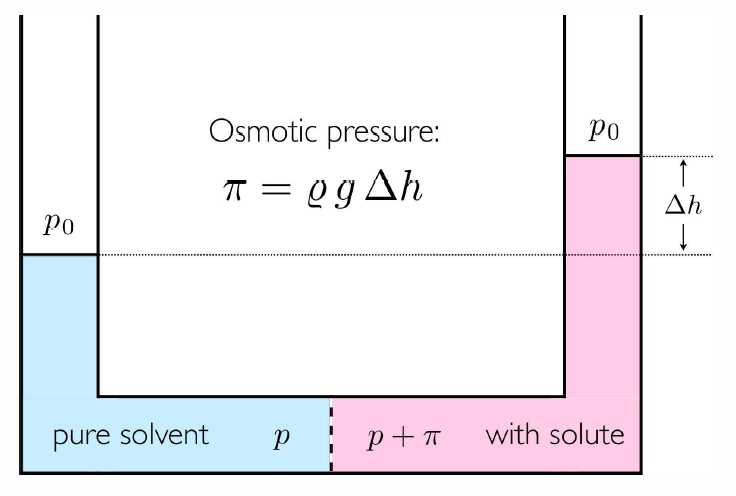
Si añadimos azúcar a una solución confinada por una membrana semipermeable ¹⁹, ¡la presión aumenta! Para ver por qué, considera una situación en la que una membrana semipermeable rígida separa una solución (solvente más solutos) de un solvente puro. Hay intercambio de energía a través de la membrana, por lo que la temperatura está a\(T\) lo largo. No hay intercambio de volumen, sin embargo:\(dV=dV'=0\), de ahí que la presión no tenga por qué ser la misma. Dado que la membrana es permeable al solvente, tenemos que el potencial químico\(\mu\ns_0\) es el mismo en cada lado. Esto significa\[g\ns_0(T,p\ns_\ssr{R})-x\kT = g\ns_0(T,p\ns_\ssr{L})\ ,\] dónde\(p\ns_\ssr{L,R}\) está la presión en los lados izquierdo y derecho de la membrana, y nuevamente\(x=N/N\ns_0\) es la concentración total de soluto. Esta ecuación nos dice una vez más que la presión\(p\) no puede ser la misma en ambos lados de la membrana. Si la diferencia de presión es pequeña, podemos expandirnos en potencias de la presión osmótica\(\pi\equiv p\ns_\ssr{R}-p\ns_\ssr{L}\,\),, y encontramos\[\pi= x\,\kT\bigg/\pabc{\mu\ns_0}{p}{T}\ .\] Pero una relación Maxwell (§ 9) garantiza\[\pabc{\mu}{p}{T,N}=\pabc{V}{N}{T,p} = v(T,p)/\NA\ ,\] dónde\(v(T,p)\) está el volumen molar del disolvente. \[\pi v=xR T\ ,\]que se parece mucho a la ley de gas ideal, ¡a pesar de que estamos hablando de soluciones densas (pero 'débiles')! La presión resultante tiene un efecto demostrable, como se esboza en la Fig. [osmótica]. Considere una solución que contenga\(\nu\) moles de sacarosa\((\RC\ns_{12}\RH\ns_{22}\RO\ns_{11})\) por kilogramo (\(55.52\,{mol}\)) de agua en\(30^\circ\,\RC\). Nos encontramos\(\pi=2.5\,{atm}\) cuando\(\nu=0.1\).

Uno podría preocuparse por la expansión de las potencias de\(\pi\) cuando\(\pi\) es mucho mayor que la presión ambiente. Pero de hecho el siguiente término en la expansión es menor que el primer término por un factor de\(\pi\kappa\ns_T\), donde\(\kappa\ns_T\) está la compresibilidad isotérmica. Para el agua se tiene\(\kappa\ns_T\approx 4.4\times 10^{-5}\,({atm})^{-1}\), de ahí que podamos ignorar con seguridad los términos de orden superior en la expansión de Taylor.

Efecto de las impurezas en los puntos de ebullición y congelación

A lo largo de la curva de coexistencia que separa las fases líquida y vapor, los potenciales químicos de las dos fases son idénticos:\[\mu^0_\ssr{L}(T,p)=\mu^0_\ssr{V}(T,p)\ .\] Aquí escribimos\(\mu^0\)\(\mu\) para enfatizar que estamos hablando de una fase sin impurezas presentes. Esta ecuación proporciona una sola restricción sobre las dos variables\(T\) y\(p\), de ahí que uno pueda, en principio, resolver para obtener\(T=T^*_0(p)\), que es la ecuación de la curva de coexistencia líquido-vapor en el\((T,p)\) plano. Ahora supongamos que hay un soluto presente en el líquido. Entonces tenemos\[\mu\ns_\ssr{L}(T,p,x)=\mu^0_\ssr{L}(T,p) - x\kT\ ,\] donde\(x\) está la concentración adimensional de soluto, sumada sobre todas las especies. La condición para la coexistencia líquido-vapor ahora se convierte\[\mu^0_\ssr{L}(T,p)-x\kT=\mu^0_\ssr{V}(T,p)\ .\] Esto conducirá a un cambio en la temperatura de ebullición fija\(p\). Asumiendo que este cambio es pequeño, expandamos al orden más bajo en\(\big(T-T^*_0(p)\big)\), escribiendo\[\mu^0_\ssr{L}(T^*_0,p)+ \pabc{\mu^0_\ssr{L}}{T}{p}\,\big(T-T^*_0\big) -x\kT = \mu^0_\ssr{V}(T^*_0,p) + \pabc{\mu^0_\ssr{V}}{T}{p}\,\big(T-T^*_0\big)\ .\] Tenga en cuenta que\[\pabc{\mu}{T}{p,N}=-\pabc{S}{N}{T,p}\] a partir de una relación Maxwell derivada de la exactitud de\(dG\). Ya que\(S\) es extenso, podemos escribir\(S=(N/\NA)\,s(T,p)\), donde\(s(T,p)\) está la entropía molar. Resolviendo para\(T\), obtenemos\[T^*(p,x)=T^*_0(p) + {xR\big[T^*_0(p)\big]^2\over \ell\ns_\Rv(p)}\ ,\] donde\(\ell\ns_\Rv=T_0^*\cdot(s\ns_\ssr{V}-s\ns_\ssr{L})\) está el calor latente de la transición líquido-vapor ²⁰. El desplazamiento\(\RDelta T^*=T^*-T_0^*\) se llama elevación del punto de ebullición.

[latentheats] Calores latentes de fusión y vaporización a\(p=1\,\) atm.

	Calor Latente	Fusión	Calor Latente de	Hervido
Sustancia	de Fusión\({\tilde \ell}_\Rf\)	Punto	Vaporización\({\tilde \ell}_\Rv\)	Punto
	\(\RJ/\Rg\)	\({}^\circ\RC\)	\(\RJ/\Rg\)	\({}^\circ\RC\)
\(\RC\ns_2\RH\ns_5\RO\RH\)	108	-114	855	78.3
\(\RN\RH\ns_3\)	339	-75	1369	-33.34
\(\RC\RO\ns_2\)	184	-57	574	-78
Él	—	—	21	-268.93
H	58	-259	455	-253
Pb	24.5	372.3	871	1750
\(\RN\ns_2\)	25.7	-210	200	-196
\(\RO\ns_2\)	13.9	-219	213	-183
\(\RH\ns_2\RO\)	334	0	2270	100

Como ejemplo, considere el agua de mar, que contiene aproximadamente\(35\,\Rg\) de disuelto\(\RN\Ra^+\RC\Rl^-\) por kilogramo de\(\RH\ns_2\RO\). Las masas atómicas de Na y Cl son\(23.0\) y\(35.4\), respectivamente, de ahí la concentración iónica total en el agua de mar (descuidando todo menos sodio y cloro) viene dada por\[x= {2\cdot 35\over 23.0 + 35.4}\bigg/{1000\over 18}\approx 0.022\ .\] El calor latente de vaporización de\(\RH\ns_2\RO\) a presión atmosférica es\(\ell=40.7\,{kJ}/{mol}\), de ahí\[\RDelta T^*={(0.022)(8.3\,\RJ/{mol}\,\RK) (373\,\RK)^2\over 4.1\times 10^4 \,\RJ/{mol}}\approx 0.6\,\RK\ .\] poner otro manera, la elevación del punto de ebullición\(\RH\ns_2\RO\) a presión atmosférica es aproximadamente\(0.28^\circ\RC\) por ciento de soluto. Podemos expresarlo como\(\RDelta T^*=Km\), donde la molalidad\(m\) es el número de moles de soluto por kilogramo de disolvente. Para\(\RH\ns_2\RO\), nos encontramos\(K=0.51^\circ\RC\,{kg}/{mol}\).

Consideraciones similares se aplican en el punto de congelación, cuando equiparamos el potencial químico del solvente más soluto al del sólido puro. El calor latente de fusión para\(\RH\ns_2\RO\) es de aproximadamente\(\ell\ns_\Rf=T^0_\Rf\cdot(s\ns_\ssr{LIQUID}-s\ns_\ssr{SOLID})=6.01\,{kJ}/{mol}\) ²¹ Predecimos así una depresión del punto de congelación de\(\RDelta T^*=-xR\big[T^*_0\big]^2/\ell\ns_\Rf=1.03^\circ\RC\cdot x[\%]\). Esto se puede expresar una vez más como\(\RDelta T^*=-Km\), con\(K=1.86^\circ\RC\,{kg}/{mol}\) ²².

Soluciones binarias

Considere una solución binaria, y escriba la energía libre de Gibbs\(G(T,p,N\ns_\SA,N\ns_\SB)\) como\[\begin{split} G(T,p,N\ns_\SA,N\ns_\SB)&=N\ns_\SA\,\mu^0_\SA(T,p) + N\ns_\SB\,\mu^0_\SB(T,p) + N\ns_\SA \kT\,\ln\bigg({N\ns_\SA\over N\ns_\SA+N\ns_\SB}\bigg)\\ &\qquad + N\ns_\SB\, \kT\,\ln\!\bigg({N\ns_\SB\over N\ns_\SA+N\ns_\SB}\bigg) + \lambda\,{N\ns_\SA N\ns_\SB\over \> N\ns_\SA+N\ns_\SB\>}\ . \end{split}\] Los primeros cuatro términos en el RHS representan la energía libre de los fluidos componentes individuales y la entropía de la mezcla. El último término es un aporte de interacción. Con\(\lambda>0\), el término de interacción prefiere que el sistema sea total\(\SA\) o completamente\(\SB\). El aporte de entropía prefiere una mezcla, por lo que hay una competencia. ¿Cuál es el estado termodinámico estable?

[bing] Energía libre de Gibbs por partícula para una solución binaria en función de la concentración\(x=x_\SB\) de la especie B (A pura en el extremo izquierdo\(x=0\>\); B puro en el extremo derecho\(x=1\)), en unidades del parámetro de interacción\(\lambda\). Curva de color rojo oscuro:\(T=0.65\,\lambda/k_\ssr{B}> T_\Rc\); curva verde:\(T=\lambda/2k_\ssr{B}=T_\Rc\); curva azul:\(T=0.40\,\lambda/k_\ssr{B} < T_\Rc\). Hemos elegido\(\mu^0_\SA=0.60\,\lambda-0.50\,k_\ssr{B}T\) y\(\mu^0_\SB=0.50\,\lambda-0.\,50\,k_\ssr{B}T\). Tenga en cuenta que la energía libre no\(g(T,p,x)\) es convexa\(x\) para\(T<T_\Rc\), lo que indica una inestabilidad y requiere una construcción Maxwell.

Es útil escribir la energía libre de Gibbs por partícula, en términos de\(g(T,p,x)=G/(N\ns_\SA+N\ns_\SB)\)\(T\)\(p\), y la concentración de la especie B (\(x\equiv x\ns_\SB=N\ns_\SB/(N\ns_\SA+N\ns_\SB)\)de ahí\(x\ns_\SA=1-x\) es la concentración de la especie A). Entonces,\[g(T,p,x)=(1-x)\,\mu^0_\SA+x\,\mu^0_\SB+ \kT\Big[x\ln x + (1-x)\ln(1-x)\Big] + \lambda\, x\,(1-x)\ .\] para que el sistema sea estable frente a la separación de fases en regiones relativamente\(\SA\)\(\SB\) ricas y ricas, debemos tener que\(g(T,p,x)\) ser una función convexa de\(x\). Nuestro primer chequeo debe ser para una inestabilidad local, descomposición espinodal. Tenemos\[{\pz g\over\pz x}=\mu^0_\SB-\mu^0_\SA + \kT\,\ln\bigg({x\over 1-x}\bigg) + \lambda\,(1-2x) \label{gpmax}\] y\[{\pz^2\!g\over\pz x^2}={\kT\over x} + {\kT\over 1-x} - 2\lambda \ .\] La espinodal viene dada por la solución a la ecuación\({\pz^2\!g\over\pz x^2}=0\), que es\[T^*(x)={2\lambda\over \kB}\,x\,(1-x)\ . \label{TSPINO}\]\(x\,(1-x)\) Since logra su valor máximo de\(\frac{1}{4}\) at\(x=\half\), tenemos\(T^*\le \kB/2\lambda\).

En la Fig. [bing] esbozamos la energía libre\(g(T,p,x)\) versus\(x\) para tres temperaturas representativas. Porque\(T>\lambda/2\kB\), la energía libre está en todas partes convexa en\(\lambda\). Cuando\(T<\lambda/2\kB\), hay energía libre se asemeja a la curva azul en la Fig. [bing], y el sistema es inestable a la separación de fases. Se dice que las dos fases son inmiscibles, o, equivalentemente, existe un hueco de solubilidad. Para determinar la curva de coexistencia, realizamos una construcción Maxwell, escribiendo\[{g(x\ns_2)-g(x\ns_1)\over x\ns_2-x\ns_1}={\pz g\over\pz x}\bigg|\nd_{x\ns_1}={\pz g\over\pz x}\bigg|\nd_{x\ns_2}\ . \label{binmax}\] Aquí,\(x\ns_1\) y\(x\ns_2\) son los límites de la región de dos fases. Estas ecuaciones admiten una simetría de\(x\leftrightarrow 1-x\), de ahí que podamos establecer\(x=x\ns_1\) y\(x\ns_2=1-x\). Encontramos\[g(1-x)-g(x)=(1-2x)\,\big(\mu_\SB^0-\mu_\SA^0\big)\ ,\] e invocamos eqns. [binmax] y [gpmax] obtenemos la solución\[T\ns_{coex}(x)={\lambda\over \kB}\cdot{1-2x\over \ \ln\big({1-x\over x}\big)\>}\ . \label{TCOEX}\]

[binmupd] Paneles superiores: cambios de potencial químico\(\RDelta\mu_\pm=\RDelta\mu_\SA\pm\RDelta\mu_\SB\) versus concentración\(x=x_\SB\). La línea negra discontinua es la espinodal, y la línea negra continua el límite de coexistencia. Las temperaturas varían de\(T=0\) (azul oscuro) a\(T=0.6\,\lambda/k_\ssr{B}\) (rojo) en unidades de\(0.1\,\lambda/k_\ssr{B}\). Paneles inferiores: diagrama de fases en los\((T,\RDelta\mu_\pm)\) planos. El punto negro es el punto crítico.

El diagrama de fases para el sistema binario se muestra en la Fig. [binario]. Porque\(T<T^*(x)\), el sistema es inestable, y se produce la descomposición espinodal. Porque\(T^*(x) < T < T\ns_{coex}(x)\), el sistema es metaestable, al igual que el gas van der Waals en su régimen correspondiente. Las soluciones binarias reales se comportan cualitativamente como el modelo aquí discutido, aunque la curva de coexistencia generalmente no es simétrica bajo\(x\leftrightarrow 1-x\), y la región monofásica se extiende hasta bajas temperaturas para\(x\approx 0\) y\(x\approx 1\). Si\(\lambda\) en sí es dependiente de la temperatura, puede haber múltiples soluciones para eqns. [TSPINO] y [TCOEX]. Por ejemplo, se podría tomar\[\lambda(T)={\lambda\ns_0\,T^2\over T^2 + T_0^2}\ .\] En este caso, tanto\(\kT > \lambda\) a temperaturas altas como bajas, y esperamos que la región monofásica sea reentrante. Tal fenómeno ocurre en mezclas de agua-nicotina, por ejemplo.

[binary] Diagrama de fases para el sistema binario. La curva negra es la curva de coexistencia, y la curva roja oscura es la espinodal. El material rico en A está a la izquierda y B a la derecha.

Es instructivo considerar el diagrama de fases en el\((T,\mu)\) plano. Definimos los cambios de potencial químico,\[\begin{aligned} \RDelta\mu\ns_\SA&\equiv\mu\ns_\SA-\mu^0_\SA=\kT\ln(1-x)+\lambda\,x^2 \\ \RDelta\mu\ns_\SB&\equiv\mu\ns_\SB-\mu^0_\SB=\kT\ln x+\lambda\,(1-x)^2\ ,\end{aligned}\] y su suma y diferencia,\(\RDelta\mu\ns_\pm\equiv\RDelta\mu\ns_\SA\pm \RDelta\mu\ns_\SB\). De la relación Gibbs-Duhem, sabemos que podemos escribir\(\mu\ns_\SB\) en función de\(T\),\(p\), y\(\mu\ns_\SA\). Como alternativa, podríamos escribir\(\RDelta\mu\ns_\pm\) en términos de\(T\),\(p\), y\(\RDelta\mu\ns_\mp\), así podemos elegir cuál de entre\(\RDelta\mu\ns_+\) y\(\RDelta\mu\ns_-\) queremos usar en nuestro diagrama de fases. Los resultados se representan en la Fig. [binmupd]. Quizás sea más fácil entender el diagrama de fases en el\((T,\RDelta\mu\ns_-)\) plano. A bajas temperaturas, por debajo\(T=T\ns_\Rc=\lambda/2\kB\), hay una transición de fase de primer orden a\(\RDelta\mu\ns_-=0\). Para\(T<T\ns_\Rc=\lambda/2\kB\) y\(\RDelta\mu\ns_-=0^+\), infinitesimalmente positivo, el sistema está en la fase\(\SA\) -rica, pero para\(\RDelta\mu\ns_-=0^-\), infinitesimalmente negativo, es\(\SB\) -rico. La concentración\(x=x\ns_\SB\) cambia discontinuamente a través del límite de fase. El punto crítico radica en\((T,\RDelta\mu\ns_-)=(\lambda/2\kB\,,\,0)\).

Si elegimos\(N=N\ns_\SA+N\ns_\SB\) ser la variable extensa, entonces fijar\(N\) significa\(dN\ns_\SA+ dN\ns_\SB=0\). Así que st fijo\(T\) y\(p\),\[dG\big|\ns_{T,p}=\mu\ns_\SA\,dN\ns_\SA + \mu\ns_\SB\,dN\ns_\SB \qquad \Rightarrow \qquad dg\big|\nd_{T,p}=-\RDelta\mu\ns_-\,dx\ .\] ya que\(\RDelta\mu\ns_-(x,T)=\vphi(x,T)-\vphi(1-x,T)=-\RDelta\mu\ns_-(1-x,T)\)\(\vphi(x,T) = \lambda x - \kT\ln x\), donde, tenemos que el límite de convivencia en el\((x,\RDelta\ns_-)\) plano es simplemente la línea\(\RDelta\mu\ns_-=0\), porque\(\int\limits_x^{1-x}\!\!\! dx'\,\RDelta\mu\ns_-(x',T)=0\).

Tenga en cuenta también que no hay región bifásica en el\((T,\RDelta\mu)\) plano; el límite de fase en este plano es una curva que termina en un punto crítico. Como vimos en el § 12, la misma situación se refiere a los\((p,v,T)\) sistemas de un solo componente. Es decir, el diagrama de fases en el\((T,v)\) plano\((p,v)\) o contiene regiones bifásicas, pero en el\((p,T)\) plano los límites entre fases son curvas unidimensionales. Cualquier comportamiento bifásico se limita a estas curvas, donde los potenciales termodinámicos son singulares.

La separación de fases se puede observar en una serie de sistemas. Un ejemplo popular involucra mezclas de agua y ouzo u otros licores a base de anís, como el arak y la absenta. Comenzando con el licor puro (\(x=1\)), y a una temperatura por debajo de la curva de coexistencia máxima, la concentración se diluye agregando agua. Siga a lo largo de la Fig. [binario] iniciando en el punto\((x=1\,,\,\kT/\lambda=0.4)\) y moviéndose hacia la izquierda. Finalmente, uno golpea el límite de la región bifásica. En este punto, la mezcla se vuelve lechosa, debido a la formación de grandes gotas de las fases puras a ambos lados de la región de coexistencia que dispersan la luz, proceso conocido como emulsificación espontánea ²³. A medida que se continúa diluyendo la solución con más agua, finalmente se pasa por toda la región de coexistencia, momento en el que la solución vuelve a ser clara, y se describe como una sola fase.

¿Qué pasa si\(\lambda<0\>\)? En este caso, tanto la entropía como la energía de interacción prefieren una fase mixta, y no hay inestabilidad a la separación de fases. Se dice que los dos fluidos son completamente miscibles. Un ejemplo sería el benceno,\(\RC\ns_6\RH\ns_6\), y el tolueno,\(\RC\ns_7\RH\ns_8\) (\(\RC\ns_6\RH\ns_5{CH}\ns_3)\). El diagrama de fases estaría en blanco, sin límites de fase por debajo de la transición de ebullición, debido a que el fluido podría existir como una mezcla en cualquier proporción.

Figura [LVCoEx] Energía libre de Gibbs por partícula\(g\) para una solución binaria ideal para temperaturas\(T\in [T^*_\SA,T^*_\SB]\). Se muestra la construcción Maxwell para el caso\(T^*_\SA < T < T^*_\SB\). Derecha: diagrama de fases, que muestra región bifásica y secuencia de destilación en\((x,T)\) el espacio.

Cualquier fluido eventualmente hervirá si la temperatura se eleva suficientemente alta. Supongamos que los puntos de ebullición de nuestros\(\SA\) y\(\SB\) fluidos son\(T^*_\ssr{A,B}\), y sin pérdida de generalidad tomemos\(T^*_\SA < T^*_\SB\) a alguna presión fija dada ²⁴. Esto significa\(\mu_\SA^\ssr{L}(T^*_\SA,p)=\mu_\SA^\ssr{V}(T^*_\SA,p)\) y\(\mu_\SB^\ssr{L}(T^*_\SB,p)=\mu_\SB^\ssr{V}(T^*_\SB,p)\). ¿Qué pasa con la mezcla? Comenzamos por escribir las energías libres de las fases mixta líquida y vapor mixta como\[\begin{aligned} g\ns_\ssr{L}(T,p,x)&=(1-x)\,\mu_\SA^\ssr{L}(T,p) + x\,\mu_\SB^\ssr{L}(T,p)+\kT\Big[x\ln x + (1-x)\ln(1-x)\Big] + \lambda\ns_\ssr{L}\,x(1-x)\\ g\ns_\ssr{V}(T,p,x)&=(1-x)\,\mu_\SA^\ssr{V}(T,p) + x\,\mu_\SB^\ssr{V}(T,p)+\kT\Big[x\ln x + (1-x)\ln(1-x)\Big] + \lambda\ns_\ssr{V}\,x(1-x) \ .\end{aligned}\] Típicamente\(\lambda\ns_\ssr{V}\approx 0\). Considera estas dos energías libres como funciones de la concentración\(x\), a fijas\(T\) y\(p\). Si las curvas nunca se cruzan, y\(g\ns_\ssr{L}(x) < g\ns_\ssr{V}(x)\) para todos\(x\in[0,1]\), entonces el líquido es siempre el estado de menor energía libre. Esta es la situación en el primer panel de la Fig. [LVCoEx]. Del mismo modo, si está\(g\ns_\ssr{V}(x) < g\ns_\ssr{L}(x)\) por encima de este rango, entonces la mezcla está en fase de vapor en todo momento. ¿Qué pasa si las dos curvas se cruzan a algún valor de\(x\)? Esta situación se representa en el segundo panel de la Fig. [LVCoEx]. En este caso, siempre hay una construcción Maxwell que disminuye la energía libre a lo largo de algún rango de concentración, el sistema sufre separación de fases.

Figura

Figura

[FAZEO] Diagramas de fases azeotrópicos negativos (izquierda) y positivos (derecha). De Wikipedia.

En un fluido ideal, tenemos\(\lambda\ns_\ssr{L}=\lambda\ns_\ssr{V}=0\), y el ajuste\(g\ns_\ssr{L}=g\ns_\ssr{V}\) requiere\[(1-x)\,\RDelta\mu\ns_\SA(T,p) + x\,\RDelta\mu\ns_\SB(T,p) = 0\ , \label{muABbin}\] donde\(\RDelta\mu\ns_{\SA/\SB}(T,p)=\mu^\ssr{L}_{\SA/\SB}(T,p)-\mu^\ssr{V}_{\SA/\SB}(T,p)\). Ampliando el potencial químico alrededor de una temperatura dada\(T^*\),\[\mu(T,p)=\mu(T^*,p) -s(T^*,p)\,(T-T^*) -{c\ns_p(T^*,p)\over 2T}\,(T-T^*)^2 + \ldots\ ,\] donde hemos utilizado\(\spabc{\mu}{T}{p,N}=-\spabc{S}{N}{T,p}=-s(T,p)\), la entropía por partícula, y\(\spabc{s}{T}{p,N}=c\ns_p/T\). Así, expandiéndose\(\RDelta\mu\ns_{\SA/\SB}\) alrededor\(T^*_{\SA/\SB}\), tenemos\[\begin{split} \RDelta\mu\ns_\SA\equiv \mu^\ssr{L}_\SA-\mu^\ssr{V}_\SA &= (s^\ssr{V}_\SA-s^\ssr{L}_\SA)(T-T^*_\SA) + {c^\ssr{V}_{p\SA}-c^\ssr{L}_{p\SA}\over 2 T^*_\SA}\,(T-T^*_\SA)^2 + \ldots \\ \RDelta\mu\ns_\SB\equiv \mu^\ssr{L}_\SB-\mu^\ssr{V}_\SB &= (s^\ssr{V}_\SB-s^\ssr{L}_\SB)(T-T^*_\SB) + {c^\ssr{V}_{p\SB}-c^\ssr{L}_{p\SB}\over 2 T^*_\SB}\,(T-T^*_\SB)^2 + \ldots \end{split}\] Suponemos\(s^\ssr{V}_{\SA/\SB} > s^\ssr{L}_{\SA/\SB}\), la fase vapor tiene mayor entropía por partícula. Así,\(\RDelta\mu\ns_{\SA/\SB}(T)\) los cambios marcan de negativo a positivo a medida que\(T\) sube a través\(T^*_{\SA/\SB}\). Si asumimos que estos son los únicos cambios de signo para\(\RDelta\mu\ns_{\SA/\SB}(T)\) en fijo\(p\), entonces la Ecuación [MuaBBin] solo se puede resolver para\(T\in [T^*_\SA,T^*_\SB]\). Esto conduce inmediatamente al diagrama de fases en el panel más a la derecha de la Fig. [LVCoEx].

[FAZZ] Energías libres antes de construcciones Maxwell para una mezcla fluida binaria en equilibrio con un vapor (Diagrama de\(\lambda_\ssr{V}=0\)). Panels show (a) \(\lambda_\ssr{L}=0\) (ideal fluid), (b) \(\lambda_\ssr{L}<0\) (miscible fluid; negative azeotrope), (c) \(\lambda^\ssr{L}_\ssr{AB}>0\) (positive azeotrope), (d) \(\lambda^\ssr{L}_\ssr{AB}>0\) (heteroazeotrope). Thick blue and red lines correspond to temperatures \(T^*_\SA\) and \(T^*_\SB\), respectively, with \(T^*_\SA < T^*_\SB\). Thin blue and red curves are for temperatures outside the range \([T^*_\SA,T^*_\SB]\). The black curves show the locus of points where \(g\) is discontinuous, where the liquid and vapor free energy curves cross. The yellow curve in (d) corresponds to the coexistence temperature for the fluid mixture. In this case the azeotrope forms within the coexistence region.

According to the Gibbs phase rule, with \(\sigma=2\), two-phase equilibrium (\(\varphi=2\)) occurs along a subspace of dimension \(d\ns_\ssr{PE}=2+\sigma-\varphi=2\). Thus, if we fix the pressure \(p\) and the concentration \(x=x\subB\), liquid-gas equilibrium occurs at a particular temperature \(T^*\), known as the boiling point. Since the liquid and the vapor with which it is in equilibrium at \(T^*\) may have different composition, different values of \(x\), one may distill the mixture to separate the two pure substances, as follows. First, given a liquid mixture of \(\SA\) and \(\SB\), we bring it to boiling, as shown in the rightmost panel of Fig. [LVcoex]. The vapor is at a different concentration \(x\) than the liquid (a lower value of \(x\) if the boiling point of pure \(\SA\) is less than that of pure \(\SB\), as shown). If we collect the vapor, the remaining fluid is at a higher value of \(x\). The collected vapor is then captured and then condensed, forming a liquid at the lower \(x\) value. This is then brought to a boil, and the resulting vapor is drawn off and condensed, etc The result is a purified \(\SA\) state. The remaining liquid is then at a higher \(\SB\) concentration. By repeated boiling and condensation, \(\SA\) and \(\SB\) can be separated. For liquid-vapor transitions, the upper curve, representing the lowest temperature at a given concentration for which the mixture is a homogeneous vapor, is called the dew point curve. The lower curve, representing the highest temperature at a given concentration for which the mixture is a homogeneous liquid, is called the bubble point curve. The same phase diagram applies to liquid-solid mixtures where both phases are completely miscible. In that case, the upper curve is called the liquidus, and the lower curve the solidus.

When a homogeneous liquid or vapor at concentration \(x\) is heated or cooled to a temperature \(T\) such that \((x,T)\) lies within the two-phase region, the mixture phase separates into the the two end components \((x^*_\ssr{L},T)\) and \((x^*_\ssr{V},T)\), which lie on opposite sides of the boundary of the two-phase region, at the same temperature. The locus of points at constant \(T\) joining these two points is called the tie line. To determine how much of each of these two homogeneous phases separates out, we use particle number conservation. If \(\eta\ns_\ssr{L,V}\) is the fraction of the homogeneous liquid and homogeneous vapor phases present, then \(\eta\ns_\ssr{L} x^*_\ssr{L} + \eta\ns_\ssr{V} x^*_\ssr{V} = x\), which says \(\eta\ns_\ssr{L}=(x-x^*_\ssr{V})/(x^*_\ssr{L}-x^*_\ssr{V})\) and \(\eta\ns_\ssr{V}=(x-x^*_\ssr{L})/(x^*_\ssr{V}-x^*_\ssr{L})\). This is known as the lever rule.

For many binary mixtures, the boiling point curve is as shown in Fig. [FAZEO]. Such cases are called azeotropes. For negative azeotropes, the maximum of the boiling curve lies above both \(T^*_{\SA,\SB}\). The free energy curves for this case are shown in panel (b) of Fig. [FAZZ]. For \(x<x^*\), where \(x^*\) is the azeotropic composition, one can distill \(\SA\) but not \(\SB\). Similarly, for \(x>x^*\) one can distill \(\SB\) but not \(\SA\). The situation is different for positive azeotropes, where the minimum of the boiling curve lies below both \(T^*_{\SA,\SB}\) , corresponding to the free energy curves in panel (c) of Fig. [FAZZ]. In this case, distillation ( condensing and reboiling the collected vapor) from either side of \(x^*\) results in the azeotrope. One can of course collect the fluid instead of the vapor. In general, for both positive and negative azeotropes, starting from a given concentration \(x\), one can only arrive at pure A plus azeotrope (if \(x<x^*\)) or pure B plus azeotrope (if \(x>x^*\)). Ethanol (C\(\ns_2\)H\(\ns_5\)OH) and water (H\(\ns_2\)O) form a positive azeotrope which is 95.6% ethanol and 4.4% water by weight. The individual boiling points are \(T^*_{\RC_2\RH_5\RO\RH}=78.4^\circ\RC\) , \(T^*_{\RH_2\RO}=100^\circ\RC\), while the azeotrope boils at \(T^*_\ssr{AZ}=78.2^\circ\RC\). No amount of distillation of this mixture can purify ethanol beyond the 95.6% level. To go beyond this level of purity, one must resort to azeotropic distillation, which involves introducing another component, such as benzene (or a less carcinogenic additive), which alters the molecular interactions.

To model the azeotrope system, we need to take \(\lambda\ns_\ssr{L}\ne 0\), in which case one can find two solutions to the energy crossing condition \(g\ns_\ssr{V}(x)=g\ns_\ssr{L}(x)\). With two such crossings come two Maxwell constructions, hence the phase diagrams in Fig. [FAZEO]. Generally, negative azeotropes are found in systems with \(\lambda\ns_\ssr{L}<0\) , whereas positive azeotropes are found when \(\lambda\ns_\ssr{L}>0\). As we’ve seen, such repulsive interactions between the \(\SA\) and \(\SB\) components in general lead to a phase separation below a coexistence temperature \(T\ns_\ssr{COEX}(x)\) given by Equation \ref{TCOEX}. What happens if the minimum boiling point lies within the coexistence region? This is the situation depicted in panel (d) of Fig. [FAZZ]. The system is then a liquid/vapor version of the solid/liquid eutectic (see Fig. [Feutectic]), and the minimum boiling point mixture is called a heteroazeotrope.

[Feutectic] fases para una mezcla eutéctica en la que un líquido está en equilibrio con dos fases sólidas\(\alpha\) y \(\beta\). El mismo diagrama de fases es válido para heteroazeótropos, donde un vapor está en equilibrio con dos fases líquidas.