4.2: El rastro mecánico cuántico

Template:MathJaxArovas

Hasta ahora nuestra comprensión de la ergodicidad está enraizada en la dinámica de la mecánica clásica. Un flujo hamiltoniano que es ergódico es aquel en el que los promedios de tiempo pueden ser reemplazados por promedios de espacio de fase usando el conjunto microcanónico. ¿Qué sucede, sin embargo, si nuestro sistema es mecánico cuántico, como todos los sistemas en última instancia lo son?

La Matriz de Densidad

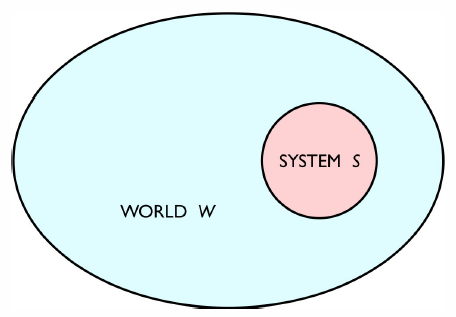
Primero, consideremos que nuestro sistema en general\(S\) estará en contacto con un mundo\(W\). Llamamos a la unión de\(S\) y\(W\) el universo,\(U=W\cup S\). Dejar\(\ket{N}\) denotar un estado mecánico cuántico de\(W\), y dejar\(\ket{n}\) denotar un estado mecánico cuántico de\(S\). Entonces la función de onda más general que podemos escribir es de la forma

\[\ket{\RPsi}=\sum_{N,n}\RPsi\nd_{N,n}\,\ket{N}\otimes\ket{n}\ .\]

Ahora vamos a calcular el valor de expectativa de algún operador\({\hat\CA}\) que actúa como la identidad dentro\(W\), es decir\(\expect{N}{\hat \CA}{N'}=\HA\,\delta\nd_{NN'}\), donde\(\HA\) está el operador 'reducido' que actúa dentro\(S\) solo. Entonces tenemos

\[\begin{split} \expect{\RPsi}{\hat \CA}{\RPsi}&=\sum_{N,N'}\sum_{n,n'}\RPsi^*_{N,n}\, \RPsi\ns_{N',n'}\, \delta\ns_{NN'}\,\expect{n}{\HA}{n'}\\ &=\Tra\!\big(\vrhhat\, \HA \big)\ , \end{split}\]

donde

\[\vrhhat=\sum_{N\nd}\sum_{n\nd,n'} \RPsi^*_{N,n}\,\RPsi\ns_{N,n'}\>\ket{n'}\,\bra{n}\]

es la matriz de densidad. La dependencia del tiempo de\(\vrhhat\) se encuentra fácilmente:

\[\begin{split} \vrhhat(t)&=\sum_{N\nd}\sum_{n\nd,n'} \RPsi^*_{N,n}\,\RPsi\ns_{N,n'}\>\ket{n'(t)}\,\bra{n(t)}\\ &=e^{-i\HH t/\hbar}\>\vrhhat\> e^{+i\HH t/\hbar}\ , \end{split}\]

donde\(\HH\) está el hamiltoniano para el sistema\(S\). Así, encontramos

\[i\hbar\,{\pz\vrhhat\over\pz t}=\big[\HH ,\vrhhat\big]\ . \label{dmevo}\]

Tenga en cuenta que la matriz de densidad evoluciona de acuerdo con una ecuación ligeramente diferente a la de un operador en la imagen de Heisenberg, para lo cual

\[\HA(t)=e^{+iHt/\hbar}\,A\,e^{-i\HH t/\hbar} \qquad\Longrightarrow\qquad i\hbar\,{\pz\HA\over\pz t}=\big[\HA,\HH\big]=-\big[\HH,\HA\big]\ .\]

Figura\(\PageIndex{1}\): Un sistema\(S\) en contacto con un 'mundo'\(W\). Se dice que la unión de los dos\(U=W\cup S\), universo, es el 'universo'.

Para los sistemas hamiltonianos, encontramos que la distribución del espacio de fase\(\vrh(q,p,t)\) evolucionó de acuerdo con la ecuación de Liouville,

\[i\,{\pz\vrh\over\pz t}=L\,\vrh\ ,\]

donde el liouvilliano\(L\) es el operador diferencial

\[L=-i\sum_{j=1}^{Nd}\Bigg\{{\pz \HH\over\pz p\ns_j}\,{\pz\over\pz q\ns_j}- {\pz \HH\over\pz q\ns_j}\,{\pz\over\pz p\ns_j}\Bigg\}\ .\]

En consecuencia, cualquier distribución\(\vrh(\Lambda\ns_1,\ldots,\Lambda\ns_k)\) que sea función de las constantes del movimiento\(\Lambda\ns_a(q,p)\) es una solución estacionaria a la ecuación de Liouville:\(\pz\ns_t\,\vrh(\Lambda\ns_1,\ldots,\Lambda\ns_k)=0\). Del mismo modo, cualquier matriz de densidad mecánica cuántica que conmute con el hamiltoniano es una solución estacionaria a la Ecuación\ ref {dmevo}. La distribución microcanónica correspondiente es

\[\vrhhat\nd_E=\delta\big(E-\HH\big)\ .\]

Promediando el DOS

Si nuestro sistema mecánico cuántico se coloca en un volumen finito, los niveles de energía serán discretos, en lugar de continuos, y la densidad de estados (DOS) será de la forma

\[D(E)=\Tra \delta\big(E-\HH\big)=\sum_l\delta(E-E\ns_l)\ ,\]

donde\(\{E\ns_l\}\) están los valores propios del hamiltoniano\(\HH\). En el límite termodinámico,\(V\to\infty\), y el espectro discreto de energías cinéticas permanece discreto para todos los finitos\(V\) pero debe acercarse al resultado continuo. Para recuperar el resultado del continuo, promediamos el DOS sobre una ventana de ancho\(\RDelta E\):

\[{\overline{D(E)}}={1\over\RDelta E}\!\!\!\int\limits_E^{E+\RDelta E}\!\!\!\!\!\!dE'\,D(E')\ .\]

Si tomamos el límite\(\RDelta E\to 0\) pero con\(\RDelta E\gg\delta E\), donde\(\delta E\) está el espaciado entre niveles cuantificados sucesivos, recuperamos una función suave, como se muestra en la Figura\(\PageIndex{2}\). En general bajaremos la barra y nos referiremos a esta función como\(D(E)\). Tenga en cuenta que\(\delta E\sim 1/D(E)=e^{-N\phi(\ve,v)}\) es (típicamente) exponencialmente pequeño en el tamaño del sistema, de ahí que si tomamos\(\RDelta E\propto V^{-1}\) cuál se desvanece en el límite termodinámico, todavía hay exponencialmente muchos niveles de energía dentro de un intervalo de ancho\(\RDelta E\).

Figura El\(\PageIndex{2}\): promedio de la densidad discreta mecánica cuántica de estados produce una curva continua.

Estados coherentes

La correspondencia cuánto-clásica se dilucidó con el uso de estados coherentes. Recordemos que el oscilador armónico unidimensional Hamiltoniano puede ser escrito

\[\begin{split} \HH\ns_0&={p^2\over 2m} + \half m\,\omega_0^2\,q^2\\ &=\hbar\omega\ns_0\,\big(a\yd a+\half\big)\ , \end{split}\]

donde\(a\) y\(a\yd\) son los operadores de escalera satisfactorios\(\big[a,a\yd\big]=1\), que se pueden tomar para ser

\[a=\ell\,{\pz\over\pz q} + {q\over 2\ell}\qquad,\qquad a\yd=-\ell\,{\pz\over\pz q} + {q\over 2\ell}\ ,\]

con\(\ell=\sqrt{\hbar/2m\omega\ns_0}\). Tenga en cuenta que

\[q=\ell\,\big(a+a\yd\big) \qquad,\qquad p={\hbar\over 2i\ell}\,\big(a-a\yd\big)\ .\]

El estado base satisface\(a\,\psi_0(q)=0\), lo que rinde

\[\psi\ns_0(q)=(2\pi\ell^2)^{-1/4}\,e^{-q^2/4\ell^2}\ .\]

El estado coherente normalizado\(\sket{z}\) se define como

\[\sket{z}= e^{-\half |z|^2}\,e^{z a\yd}\sket{0} =e^{-\half |z|^2}\sum_{n=0}^\infty {z^n\over\sqrt{n!}}\>\sket{n}\ .\]

La superposición de estados coherentes viene dada por

\[\sbraket{z_1}{z_2}=e^{-\half |z\nd_1|^2}\,e^{-\half |z\nd_2|^2}\, e^{\zbar\nd_1 z\nd_2}\ ,\]

de ahí que diferentes estados coherentes no sean ortogonales. A pesar de esta no ortogonalidad, los estados coherentes permiten una simple resolución de la identidad,

\[1=\int\!\!{d^2\!z\over 2\pi i}\>\sket{z}\sbra{z} \quad ; \quad {d^2\!z\over 2\pi i}\equiv {d\, { Re} z\ d\,{ Im} z\over \pi}\]

que es sencillo de establecer.

Para obtener cierta intuición física sobre los estados coherentes, defina

\[z\equiv {Q\over 2\ell} +{i\ell P\over\hbar}\]

y escribir\(\sket{z}\equiv\sket{Q,P}\). Uno encuentra (¡ejercicio! )

\[\psi\nd_{Q,P}(q)=\sbraket{q}{z}=(2\pi\ell^2)^{-1/4}\, e^{-iPQ/2\hbar}\,e^{iPq/\hbar}\,e^{-(q-Q)^2/4\ell^2}\ ,\]

de ahí que el estado coherente\(\psi\nd_{Q,P}(q)\) es un conjunto de ondas Gaussianly localizado alrededor\(q=Q\), pero oscilando con el impulso promedio\(P\).

Por ejemplo, podemos calcular

\[\begin{aligned} \expect{Q,P}{q}{Q,P}&=\expect{z}{\ell\,(a+a\yd)}{z}=2\ell\>{ Re}\,z=Q\\ \expect{Q,P}{p}{Q,P}&=\expect{z}{{\hbar\over 2i\ell}\,(a-a\yd)}{z}={\hbar\over\ell}\>{ Im}\,z=P\end{aligned}\]

así como

\[\begin{aligned} \expect{Q,P}{q^2}{Q,P}&=\expect{z}{\ell^2\,(a+a\yd)^2}{z}=Q^2+\ell^2\\ \expect{Q,P}{p^2}{Q,P}&=-\expect{z}{{\hbar^2\over 4\ell^2}(a-a\yd)^2}{z}=P^2+ {\hbar^2\over 4\ell^2}\ .\end{aligned}\]

Así, las fluctuaciones de raíz cuadrática media en el estado coherente\(\sket{Q,P}\) son

\[\RDelta q = \ell=\sqrt{\hbar\over 2m\omega\ns_0} \qquad,\qquad \RDelta p={\hbar\over 2\ell} =\sqrt{m\hbar\omega\ns_0\over 2},\]

y\(\RDelta q\cdot\RDelta p =\half\,\hbar\). Así aprendemos que el estado coherente\(\psi\ns_{Q,P}(q)\) se localiza en el espacio de fase, tanto en posición como en impulso. Si tenemos un operador general\(\HA(q,p)\), entonces podemos escribir

\[\expect{Q,P}{\HA(q,p)}{Q,P}=A(Q,P) + \CO(\hbar)\ ,\]

de donde\(A(Q,P)\) se forma\(\HA(q,p)\) reemplazando\(q\to Q\) y\(p\to P\).

Desde

\[{d^2\!z\over 2\pi i}\equiv {d\, { Re} z\ d\,{ Im} z\over \pi}={dQ\,dP\over 2\pi\hbar}\ ,\]

podemos escribir el rastro usando estados coherentes como

\[\Tra \HA={1\over 2\pi\hbar}\int\limits_{-\infty}^\infty\!\!\!dQ\!\!\int\limits_{-\infty}^\infty\!\!\!dP\> \expect{Q,P}{\HA\,}{Q,P}\ .\]

Ahora podemos entender el origen del factor\(2\pi\hbar\) en el denominador de cada\((q\nd_i,p\nd_i)\) integral sobre el espacio de fase clásico en la Ecuación\ ref {trcl}.

Obsérvese que\(\omega\ns_0\) es arbitrario en nuestra discusión. Al aumentar\(\omega\ns_0\), los estados se vuelven más localizados en\(q\) y más onda plana como en\(p\). Sin embargo, mientras\(\omega\ns_0\) sea finito, el ancho del estado coherente en cada dirección es proporcional a\(\hbar^{1/2}\), y así desaparece en el límite clásico.