8.4: Aproximación del Tiempo de Relajación

Template:MathJaxArovas

Aproximación de la Integral de Colisión

Consideramos ahora un modelo muy simple de la colisión integral,

\[\coll=-\,{f-f^0\over\tau}=-{\delf\over\tau}\ .\]

Este modelo se conoce como la aproximación del tiempo de relajación. Aquí,\(f^0=f^0(\Br,\Bp,t)\) es una función de distribución que describe un equilibrio local en cada posición\(\Br\) y tiempo\(t\). La cantidad\(\tau\) es el tiempo de relajación, que en principio puede ser dependiente del momento, pero que primero consideraremos constante. A falta de términos de streaming, tenemos

\[{\pz \,\delf\over\pz t}=-{\delf\over\tau} \qquad\Longrightarrow\qquad \delf(\Br,\Bp,t)=\delf(\Br,\Bp,0)\,e^{-t/\tau}\ .\]

La distribución\(f\) luego se relaja a la distribución de equilibrio\(f^0\) en una escala de tiempo\(\tau\). Observamos que esta aproximación es obviamente defectuosa en el sentido de que todas las cantidades —incluso los invariantes colisionales— se relajan a sus valores de equilibrio en la escala\(\tau\). En el Apéndice, consideramos un modelo para la integral de colisión en el que se conservan todos los invariantes colisionales, pero todo lo demás se relaja al equilibrio local a una sola velocidad.

Computación del tiempo de dispersión

Considera dos partículas con velocidades\(\Bv\) y\(\Bv'\). El promedio de su velocidad relativa es

\[\langle \,|\Bv-\Bv'|\, \rangle = \int\!\!d^3\!v\!\int\!\!d^3\!v'\>P(\Bv)\,P(\Bv')\,|\Bv-\Bv'|\ ,\]

donde\(P(\Bv)\) está la distribución de velocidad Maxwell,

\[P(\Bv)=\bigg({m\over 2\pi\kT}\bigg)^{\!\!3/2}\exp\bigg(\!-\!{m\Bv^2\over 2\kT}\bigg)\ ,\]

que se desprende de la forma Boltzmann de la distribución de equilibrio\(f^0(\Bp)\). Se deja como ejercicio para que el alumno verifique que

\[{\bar v}\ns_{rel} \equiv \langle \,|\Bv-\Bv'|\, \rangle= {4\over \sqrt{\pi}}\,\bigg({\kT\over m}\bigg)^{\!\!1/2}\ .\]

Tenga en cuenta que\({\bar v}\ns_{rel} = \sqrt{2} \,{\bar v}\), donde\({\bar v}\) está la velocidad promedio de las partículas. Dejar\(\sigma\) ser la sección transversal de dispersión total, que para las esferas duras es\(\sigma=\pi d^2\), donde\(d\) está el diámetro de la esfera dura. Entonces la velocidad a la que las partículas se dispersan es

\[{1\over\tau}=n\, {\bar v}\ns_{rel}\, \sigma\ . \label{nutaueqn}\]

El camino libre medio de partículas es simplemente

\[\ell={\bar v}\,\tau={1\over\sqrt{2}\,n\,\sigma}\ .\]

Si bien la longitud de dispersión no depende de la temperatura dentro de este formalismo, el tiempo de dispersión es\(T\) -dependiente, con

\[\tau(T)={1\over n\,{\bar v}\ns_{rel} \, \sigma} = {\sqrt{\pi}\over 4 n\sigma}\bigg({m\over\kT}\bigg)^{\!\!1/2}\ .\]

As\(T\to 0\), el tiempo de colisión diverge como\(\tau\propto T^{-1/2}\), debido a que las partículas en promedio se mueven más lentamente a temperaturas más bajas. El camino libre medio, sin embargo, es independiente de\(T\), y viene dado por\(\ell=1/\sqrt{2}n\sigma\).

Figura\(\PageIndex{1}\): Representación gráfica de la ecuación\(n\,\sigma\,{\bar v}_{rel}\,\tau=1\), que produce el tiempo de dispersión\(\tau\) en términos de densidad numérica\(n\)\({\bar v}_{rel}\), velocidad relativa promedio del par de partículas y sección transversal de dispersión total de dos partículas\(\sigma\). La ecuación dice que en promedio debe haber una partícula dentro del tubo.

Conductividad térmica

Consideramos un sistema con gradiente de temperatura\(\bnabla T\) y buscamos una solución en estado estacionario (independiente del tiempo) a la ecuación de Boltzmann. Asumimos\(F\ns_\alpha=\CQ\ns_{\alpha\beta}=0\). Apelando a la ecuación\ ref {bwig}, y usando la aproximación del tiempo de relajación para la integral de colisión, tenemos

\[\delta \!f=-{\tau (\ve-c\ns_p\,T)\over\kB T^2}\,(\Bv\cdot\bnabla T)\,f^0\ .\]

Ahora estamos listos para calcular la energía y las corrientes de partículas. Para calcular la densidad local de cualquier cantidad\(A(\Br,\Bp)\), multiplicamos por la distribución\(f(\Br,\Bp)\) e integramos sobre el impulso:

\[\rho\nd_{\!A\nd}(\Br,t)=\int\!\! d^3\!p \,A(\Br,\Bp)\,f(\Br,\Bp,t)\ ,\]

Para la corriente energética (térmica), dejamos\(A= \ve\, v\ns_\alpha=\ve\,p\ns_\alpha/m\), en cuyo caso\(\rho\nd_{\!A\nd}=j\ns_\alpha\). Nótese que\(\int\!\!d^3\!p\>\Bp\,f^0=0\) ya que\(f^0\) es isotrópico en\(\Bp\) incluso cuando\(\mu\) y\(T\) dependa de\(\Br\). Así, sólo\(\delf\) entra en el cálculo de las diversas corrientes. Así, la corriente de energía (térmica) es

\[\begin{split} j^\alpha_\ve(\Br)&=\int\!\! d^3\!p \> \ve\,v^\alpha\,\delf\\ &=-{n\tau\over\kB T^2}\, \blangle \, v^\alpha v^\beta \,\ve\,(\ve-c\ns_p\,T) \, \brangle\,{\pz T\over\pz x^\beta}\ , \label{jtheqn} \end{split}\]

donde\(\beta\) se suma el índice repetido y donde los promedios de impulso se definen en relación con la distribución de equilibrio,

\[\langle \, \phi(\Bp) \, \rangle = \int\!\! d^3\!p \,\phi(\Bp)\,f^0(\Bp)\bigg/\!\!\int\!\! d^3\!p \,f^0(\Bp) =\!\!\int\!\!d^3\!v\>P(\Bv)\,\phi(m\Bv)\ .\]

En este contexto, es útil señalar la identidad

\[d^3\!p \,f^0(\Bp)=n\,d^3\!v\>P(\Bv)\ ,\]

donde

\[P(\Bv)=\bigg({m\over 2\pi\kT}\bigg)^{\!3/2}\>e^{-m(\Bv-\BV)^2/2\kT}\]

es la distribución de velocidad Maxwell.

Tenga en cuenta que si\(\phi=\phi(\ve)\) es una función de la energía, y si\(\BV=0\), entonces

\[d^3\!p \,f^0(\Bp)=n\,d^3\!v\>P(\Bv)=n\,{\widetilde P}(\ve)\,d\ve\ ,\]

donde

\[{\widetilde P}(\ve)=\frac{2}{\sqrt{\pi}} (\kT)^{-3/2}\,\ve^{1/2}\,e^{-\ve/\kT}\ ,\]

es la distribución maxwelliana de las energías de partículas individuales. Esta distribución se normaliza con\(\int\limits_0^\infty\!d\ve\,{\widetilde P}(\ve)=1\). Los promedios con respecto a esta distribución están dados por

\[\langle\,\phi(\ve)\,\rangle=\int\limits_0^\infty\!\!d\ve\>\phi(\ve)\,{\widetilde P}(\ve) =\frac{2}{\sqrt{\pi}} (\kT)^{-3/2}\!\!\int\limits_0^\infty\!\!d\ve\>\ve^{1/2}\,\phi(\ve)\,e^{-\ve/\kT}\ .\]

Si\(\phi(\ve)\) es homogéneo, entonces para cualquiera\(\alpha\) tenemos

\[\langle\,\ve^\alpha\,\rangle=\frac{2}{\sqrt{\pi}}\RGamma\big(\alpha+\frac{3}{2}\big) (\kT)^\alpha\ .\]

Debido a la isotropía espacial, está claro que podemos reemplazar

\[v^\alpha\,v^\beta \to \third\Bv^2\,\delta\ns_{\alpha\beta} = {2\ve\over 3m}\,\delta\ns_{\alpha\beta}\]

en Ecuación\ ref {jtheqn}. Entonces tenemos\(\Bj\ns_\ve=-\kappa\,\bnabla T\), con

\[\kappa={2n\tau\over 3m\kB T^2}\,\langle\, \ve^2\big(\ve-c\ns_p\,T\big)\,\rangle = 5n\tau \dfrac{\kB^2 T}{ 2m}=\frac{\pi}{8} n\ell{\bar v}\,c\ns_p\ ,\]

donde hemos usado\(c \ns_p =\frac{5}{2}\kB\) y\(\vbar^2=\frac{8k_{B}T}{\pi m}\). La cantidad\(\kappa\) se llama conductividad térmica. Tenga en cuenta que\(\kappa\propto T^{1/2}\).

Viscosidad

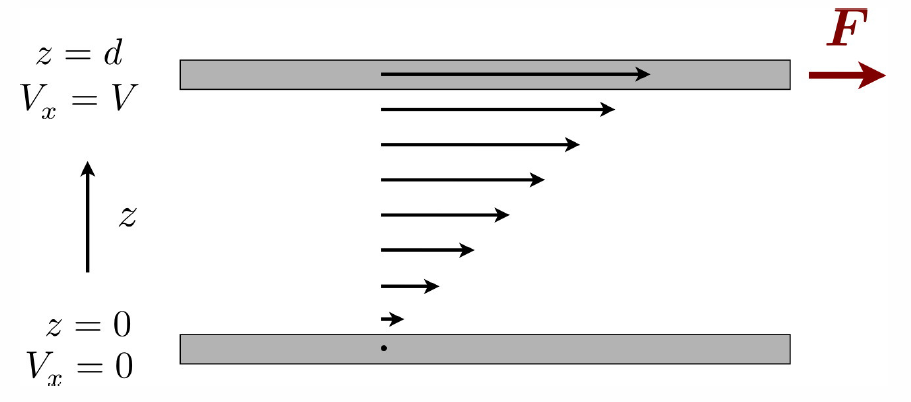
Considera la situación representada en la Figura\(\PageIndex{2}\). Un fluido que llena el espacio entre dos placas planas grandes en\(z=0\) y\(z=d\) se pone en movimiento por una fuerza\(\BF=F\HBx\) aplicada a la placa superior; la placa inferior es fija. Se supone que la velocidad del fluido coincide localmente con la de las placas. Las partículas fluidas en la parte superior tienen un\(x\) componente promedio de su momento\(\langle p\ns_x\rangle=mV\). A medida que estas partículas se mueven hacia abajo hacia\(z\) valores más bajos, traen consigo sus\(x\) -momenta. Por lo tanto hay un flujo descendente (\(-\zhat\)-dirigido) de\(\langle p\ns_x\rangle\). Dado que\(x\) el impulso se aleja constantemente del\(z=d\) plano, esto significa que hay un arrastre viscoso\(-\Bx\) dirigido en la placa superior. La fuerza de arrastre viscoso por unidad de área viene dada por\(F\ns_{drag}/A=-\eta V/d\), donde\(V/d=\pz V\ns_x/\pz z\) está el gradiente de velocidad y\(\eta\) es la viscosidad de cizallamiento. En estado estacionario, la fuerza aplicada equilibra la fuerza de arrastre,\(F+F\ns_{drag}=0\). Claramente en el estado estacionario la densidad neta de momento del fluido no cambia, y viene dada por\(\half\rho V\HBx\), donde\(\rho\) esta la densidad de masa del fluido. El momento por unidad de tiempo inyectado en el fluido por la placa superior en\(z=d\) es entonces extraído por la placa inferior en\(z=0\). La densidad de flujo de momento\(\RPi\ns_{xz}=n\,\langle\,p\ns_x\,v\ns_z\,\rangle\) es la fuerza de arrastre en la superficie superior por unidad de área:\(\RPi\ns_{xz}=-\eta\,{\pz V\ns_x\over\pz z}\). Las unidades de viscosidad son\([\eta]=M/LT\).

Ahora proporcionamos algunas definiciones formales de viscosidad. Como veremos actualmente, existe de hecho un segundo tipo de viscosidad, llamada segunda viscosidad o viscosidad aparente, que es medible aunque no por el tipo de experimento representado en igure\(\PageIndex{2}\).

El tensor de flujo de impulso\(\RPi\ns_{\alpha\beta}=n\,\langle\,p\ns_\alpha\,v\ns_\beta\,\rangle\) se define como la corriente de componente de impulso\(p\ns_\alpha\) en la dirección de aumento\(x\ns_\beta\). Para un gas en movimiento con velocidad promedio\(\BV\!\), tenemos

\[\begin{split} \RPi\ns_{\alpha\beta}&=nm\,\langle\,(V\ns_\alpha+v'_\alpha)(V\ns_\beta+v'_\beta)\,\rangle\\ &=nm\, V\ns_\alpha V\ns_\beta + nm\,\langle\,v'_\alpha v'_\beta\,\rangle\\ &=nm\, V\ns_\alpha V\ns_\beta+\third nm\,\langle\,{\Bv'}^2\,\rangle\,\delta\ns_{\alpha\beta}\\ &=\rho\, V\ns_\alpha V\ns_\beta+p\,\delta\ns_{\alpha\beta}\ , \end{split}\]

donde\(\Bv'\) es la velocidad de las partículas en un marco moviéndose con la velocidad\(\BV\!\), y donde hemos invocado la ley ideal del gas\(p=n\kT\). La densidad de masa es\(\rho=nm\).

Figura\(\PageIndex{2}\): Experimento Gedankenpara medir la viscosidad de cizallamiento\(\eta\) en un fluido. La placa inferior es fija. La fuerza de arrastre viscoso por unidad de área en la placa superior es\(F_{drag}/A=-\eta V/d\). Esto debe ser equilibrado por una fuerza aplicada\(F\).

Cuando\(\BV\) varía espacialmente,

\[\RPi\ns_{\alpha\beta}=p\,\delta\ns_{\alpha\beta} + \rho\, V\ns_\alpha V\ns_\beta -{\tilde\sigma}_{\alpha\beta}\ ,\]

donde\({\tilde\sigma}\ns_{\alpha\beta}\) está el tensor de esfuerzo de viscosidad. Cualquier tensor simétrico, como\({\tilde\sigma}\ns_{\alpha\beta}\), puede descomponerse en una suma de (i) un componente sin rastro, y (ii) un componente proporcional a la matriz de identidad. Dado que\({\tilde\sigma}\ns_{\alpha\beta}\) debe ser, a primer orden, lineal en las derivadas espaciales de los componentes del campo de velocidad\(\BV\), hay una descomposición única de dos parámetros:

\[\begin{split} {\tilde\sigma}_{\alpha\beta}&=\eta\Bigg( {\pz V\ns_\alpha\over\pz x\ns_\beta} + {\pz V\ns_\beta\over\pz x\ns_\alpha} -\frac{2}{3}\,\bnabla\!\cdot\!\BV\,\delta\ns_{\alpha\beta}\bigg) +\zeta\,\bnabla\!\cdot\!\BV\,\delta\ns_{\alpha\beta}\\ &=2\eta\,\Big(\CQ\ns_{\alpha\beta}-\third\Tra(\CQ)\,\delta\ns_{\alpha\beta}\Big) + \zeta\,\Tra(\CQ)\,\delta\ns_{\alpha\beta}\ . \end{split}\]

El coeficiente del componente sin trazas es\(\eta\), conocido como viscosidad de cizallamiento. El coeficiente del componente proporcional a la identidad es\(\zeta\), conocido como la viscosidad aparente. El tensor de estrés completo\(\sigma\ns_{\alpha\beta}\) contiene una contribución de la presión:

\[\sigma\ns_{\alpha\beta}=-p\,\delta\ns_{\alpha\beta} + {\tilde\sigma}\ns_{\alpha\beta}\ .\]

La fuerza diferencial\(dF\ns_\alpha\) que ejerce un fluido sobre un elemento de superficie\(\nhat\,dA\) es

\[dF\ns_\alpha=-\sigma\ns_{\alpha\beta}\,n\ns_\beta\,dA\ ,\]

donde estamos usando la convención de suma de Einstein y sumando sobre el índice repetido\(\beta\). Ahora calcularemos la viscosidad de cizallamiento\(\eta\) usando la ecuación de Boltzmann en la aproximación del tiempo de relajación.

Apelando de nuevo a la ecuación\ ref {bwig}, con\(\BF=0\) y\(h=c\ns_p T\), encontramos

\[\delf=-{\tau\over\kT}\Bigg\{ m\, v\ns_\alpha v\ns_\beta\,\CQ\ns_{\alpha\beta} +{\ve-c\ns_p\,T\over T}\>\Bv\cdot\bnabla T -{\ve\over c\ns_V/\kB}\,\bnabla\ncdot\BV\Bigg\}\>f^0\ .\]

Suponemos\(\bnabla T=\bnabla\ncdot\BV=0\), y calculamos el flujo de impulso:

\[\begin{split} \RPi\ns_{xz}&=n\!\int\!\! d^3\!p \> p\ns_x v\ns_z\,\delf\\ &=-{nm^2\tau \over \kT}\>\CQ\ns_{\alpha\beta} \>\langle\,v\ns_x\,v\ns_z\,v\ns_\alpha\,v\ns_\beta\,\rangle\\ &=-{n\tau\over\kT}\bigg({\pz V\ns_x\over\pz z} + {\pz V\ns_z\over\pz x}\bigg) \, \langle\, mv_x^2\cdot mv_z^2\,\rangle\\ &=-n\tau\kT \bigg({\pz V\ns_z\over\pz x} + {\pz V\ns_x\over\pz z}\bigg)\ . \end{split}\]

Así, si\(V\ns_x=V\ns_x(z)\), tenemos

\[\RPi\ns_{xz}=-n\tau \kT\,{\pz V\ns_x\over\pz z}\]

de la que leemos la viscosidad,

\[\eta= n\kT\tau=\frac{\pi}{8} nm\ell{\bar v} \ .\]

Tenga en cuenta que\(\eta(T)\propto T^{1/2}\).

Figura\(\PageIndex{3}\): Izquierda: conductividad térmica (\(\lambda\)en figura) de Ar entre\(T=800\,\RK\) y\(T=2600\,\RK\). El mejor ajuste a una sola ley de poder\(\lambda=aT^b\) resulta en\(b=0.651\). Fuente: G. S. Springer y E. W. Wingeier, J. Chem Phys. 59, 1747 (1972). Derecha: gráfico log-log de viscosidad de cizallamiento (\(\mu\)en figura) de He entre\(T\approx 15\,\RK\) y\(T\approx 1000\,\RK\). La línea roja tiene pendiente\(\half\). La pendiente de los datos es aproximadamente\(0.633\). Fuente: J. Kestin y W. Leidenfrost, Physica 25, 537 (1959).

¿Qué tan bien aguantan estas predicciones? En igure\(\PageIndex{3}\), trazamos datos para la conductividad térmica del argón y la viscosidad de cizallamiento del helio. Ambos muestran un claro comportamiento sublineal en función de la temperatura, pero la pendiente\(d\ln\kappa/d\ln T\) es aproximadamente\(0.65\) y\(d\ln\eta/d\ln T\) es aproximadamente\(0.63\). Claramente el modelo simple ni siquiera está consiguiendo la dependencia funcional del\(T\) derecho, y mucho menos su coeficiente. Aún así, nuestra teoría cruda es al menos cualitativamente correcta.

¿Por qué ambos así\(\kappa(T)\) como\(\eta(T)\) disminuir a bajas temperaturas? La razón es que la corriente de calor que fluye en respuesta a, así\(\bnabla T\) como la corriente de impulso que fluye en respuesta a,\(\pz V\ns_x/\pz z\) se deben a la presencia de colisiones, que resultan en la transferencia de impulso y energía entre partículas. Esto es cierto incluso cuando se conservan la energía total y el impulso, que no están en la aproximación del tiempo de relajación. Intuitivamente, podríamos pensar que la viscosidad debería aumentar a medida que se baja la temperatura, ya que la experiencia común nos dice que los fluidos se “encariñan” a medida que se enfrían —piensen en la miel como un ejemplo extremo. Pero claro que la miel no se parece en nada a un gas ideal, y la física detrás de la cristalización o transición vítrea que ocurre en los fluidos reales cuando se enfrían suficientemente está completamente ausente de nuestro enfoque. En nuestro cálculo, la viscosidad resulta de colisiones, y sin colisiones no hay transferencia de momento y por lo tanto no hay viscosidad. Si, por ejemplo, las partículas de gas simplemente pasaran unas a otras, como si fueran fantasmas, entonces no habría oposición a mantener un gradiente de velocidad arbitrario.

Fuerza externa oscilante

Supongamos que\(\BF\ns_{ext}(t)=\BF\,e^{-i\omega t}\) se aplica una fuerza externa oscilante uniforme. Para un sistema de partículas cargadas, esta fuerza surgiría de un campo eléctrico externo\(\BF\ns_{ext}=q\BE\,e^{-i\omega t}\), donde\(q\) está la carga de cada partícula. Vamos a asumir\(\bnabla T=0\). Luego se escribe la ecuación de Boltzmann

\[{\pz f\over\pz t}+{\Bp\over m}\cdot{\pz f\over\pz \Br} +\BF e^{-i\omega t}\cdot{\pz f\over\pz\Bp}= -{f-f^0\over \tau}\ .\]

Escribimos de nuevo\(f=f^0+\delf\), y asumimos que\(\delf\) es espacialmente constante. Por lo tanto,

\[{\pz\,\delf\over\pz t} + \BF e^{-i\omega t}\cdot\Bv\,{\pz f^0\over\pz\ve} = -{\delf\over\tau}\ .\]

Si asumimos\(\delf(t)=\delf(\omega)\,e^{-i\omega t}\) entonces la ecuación diferencial anterior se convierte en una ecuación algebraica, con solución

\[\delf(t)=-{\tau\,e^{-i\omega t}\over 1-i\omega \tau}\>{\pz f^0\over\pz\ve}\>\BF\cdot\Bv\ .\]

Ahora calculamos la corriente de partícula:

\[\begin{split} j\ns_\alpha(\Br,t)&=\int\!\! d^3\!p \>\Bv\>\delf\\ &={\tau\,e^{-i\omega t}\over 1-i\omega \tau}\cdot{F\ns_\beta\over\kT}\!\!\int\!\! d^3\!p \>f^0(\Bp)\,v\ns_\alpha\,v\ns_\beta\bvph\\ &={\tau\,e^{-i\omega t}\over 1-i\omega \tau}\cdot{n F\ns_\alpha\over 3\kT}\!\!\int\!\!d^3\!v\>P(\Bv)\,\Bv^2\bvph\\ &={n\tau\over m}\cdot{F\ns_\alpha\,e^{-i\omega t}\over 1-i\omega \tau}\ . \end{split}\]

Si las partículas son electrones, con carga\(q=-e\), entonces la corriente eléctrica es\((-e)\) multiplicada por la corriente de partículas. Luego obtenemos

\[j^\ssr{(elec)}_\alpha(t)={ne^2\tau\over m}\cdot {E\ns_\alpha\,e^{-i\omega t}\over 1-i\omega \tau}\equiv\sigma\ns_{\alpha\beta}(\omega) \>E\ns_\beta\,e^{-i\omega t}\ ,\]

donde

\[\sigma\ns_{\alpha\beta}(\omega)={ne^2\tau\over m}\cdot{1\over 1-i\omega\tau}\,\delta\ns_{\alpha\beta}\]

es el tensor de conductividad eléctrica dependiente de la frecuencia. Por supuesto, para fermiones como los electrones, deberíamos estar usando la distribución Fermi en lugar de la distribución Maxwell-Boltzmann para\(f^0(\Bp)\). Esto afecta la relación entre\(n\) y\(\mu\) solo, y el resultado final para el tensor de conductividad\(\sigma\ns_{\alpha\beta}(\omega)\) no cambia.

Tratamiento Rápido y Sucio del Transporte

Supongamos que tenemos alguna cantidad intensiva promediada\(\phi\) que es espacialmente dependiente a través de\(T(\Br)\) o\(\mu(\Br)\) o\(\BV(\Br)\). Por simplicidad vamos a escribir\(\phi=\phi(z)\). Deseamos calcular la corriente de\(\phi\) a través de alguna superficie cuya ecuación es\(dz=0\). Si la trayectoria libre media es\(\ell\), entonces el valor de\(\phi\) para las partículas que cruzan esta superficie en la\(+\zhat\) dirección es\(\phi(z-\ell\cos\theta)\), donde\(\theta\) está el ángulo que hace la velocidad de la partícula con respecto a\(\zhat\),\(\cos\theta=v\ns_z/v\). Realizamos el mismo análisis para partículas que se mueven en la\(-\zhat\) dirección, para lo cual\(\phi=\phi(z+\ell\cos\theta)\). La corriente de\(\phi\) a través de esta superficie es entonces

\[\begin{split} \Bj\ns_\phi&=n\zhat\!\!\!\int\limits_{v\ns_z >0}\!\!\!\!d^3\!v\,P(\Bv)\,v\ns_z\,\phi(z-\ell\cos\theta) +n\zhat\!\!\!\int\limits_{v\ns_z<0}\!\!\!\!d^3\!v\,P(\Bv)\,v\ns_z\,\phi(z+\ell\cos\theta)\\ &=-n\ell\,{\pz\phi\over\pz z}\zhat\!\int\!\!d^3\!v\>P(\Bv)\,{v^2_z\over v}=-\third n{\bar v}\ell\,{\pz\phi\over\pz z}\,\zhat\ , \end{split}\]

donde\({\bar v}=\sqrt{\frac{8k_{B}T}{\pi m}}\) es la velocidad promedio de las partículas. Si la\(z\) -dependencia de\(\phi\) viene a través de la\(\phi\) dependencia de la temperatura local\(T\), entonces tenemos

\[\Bj\ns_\phi=-\third\,n\ell{\bar v}\,{\pz\phi\over\pz T}\,\bnabla T \equiv -K\,\bnabla T\ ,\]

donde

\[K=\third n\ell {\bar v}\,{\pz\phi\over\pz T}\]

es el coeficiente de transporte. Si\(\phi=\langle\ve\rangle\), entonces\(\frac{\pz\phi}{\pz T}=c\nd_p\), dónde\(c\nd_p\) está la capacidad calorífica por partícula a presión constante. Luego encontramos\(\Bj\ns_\ve=-\kappa\,\bnabla T\) con conductividad térmica

\[\kappa=\third n\ell{\bar v}\, c\nd_p\ .\]

Nuestro cálculo de la ecuación de Boltzmann arrojó el mismo resultado, pero con un prefactor de\(\frac{\pi}{8}\) en lugar de\(\third\).

Podemos hacer un argumento similar para la viscosidad. En este caso\(\phi=\langle p\ns_x\rangle\) está variando espacialmente a través de su dependencia de la velocidad del flujo\(\BV(\Br)\). Claramente\(\pz\phi/\pz V\ns_x=m\), de ahí

\[j^z_{p\ns_x}=\RPi\ns_{xz}=-\third nm\ell{\bar v} \,{\pz V\ns_x\over\pz z}\ ,\]

a partir del cual identificamos la viscosidad,\(\eta=\third nm\ell {\bar v}\). Una vez más, esto concuerda en sus dependencias funcionales con el cálculo de la ecuación de Boltzmann en la aproximación del tiempo de relajación. Sólo difieren los coeficientes. La relación de los coeficientes es\(K\ns_\ssr{QDC}/K\ns_\ssr{BRT}=\frac{8}{3\pi}=0.849\) en ambos casos ⁶.

Difusividad térmica, viscosidad cinemática y número Prandtl

Supongamos que, bajo condiciones de presión constante, agregamos calor\(q\) por unidad de volumen a un gas ideal. Sabemos por la termodinámica que su temperatura luego aumentará en una cantidad\(\RDelta T=q/nc\ns_p\). Si\(\Bj\ns_q\) fluye una corriente de calor, entonces la ecuación de continuidad para el flujo de energía requiere

\[nc\ns_p\,{\pz T\over\pz t} + \bnabla\cdot \Bj\ns_q=0\ .\]

En un sistema donde no hay corriente neta de partículas, la corriente térmica\(\Bj\ns_q\) es la misma que la corriente de energía\(\Bj\ns_\ve\), y ya que\(\Bj\ns_\ve=-\kappa\,\bnabla T\), obtenemos una ecuación de difusión para la temperatura,

\[{\pz T\over \pz t}={\kappa\over n c\ns_p}\,\nabla^2 T\ .\]

La combinación

\[a\equiv {\kappa\over n c\ns_p}\]

se conoce como la difusividad térmica. Nuestro cálculo de la ecuación de Boltzmann en la aproximación del tiempo de relajación arrojó el resultado\(\kappa=n\kT\tau c\ns_p/m\). Así, nos encontramos\(a=\kT\tau/m\) a través de este método. Tenga en cuenta que las dimensiones de\(a\) son las mismas que para cualquier constante de difusión\(D\), a saber\([a]=L^2/T\).

[Prandtl] Viscosidades, conductividades térmicas y números de Prandtl para algunos gases comunes en\(T=293\,\RK\) y\(p=1\,\) atm. (Fuente: Cuadro 1.1 de Smith y Jensen, con datos para gases triatómicos añadidos.)

Gas	\(\eta\)(\(\mu{Pa}\cdot\Rs\))	\(\kappa\)(\({mW}/\Rm\cdot\RK\))	\(c\ns_p/\kB\)	\({Pr}\)
Él	\ (\ eta\) (\(\mu{Pa}\cdot\Rs\))” style="text-align:center; vertical-align:middle; ">\(19.5\)	\ (\ kappa\) (\({mW}/\Rm\cdot\RK\))” style="text-align:center; vertical-align:middle; ">\(149\)	\ (c\ ns_p/\ kB\)” style="text-align:center; vertical-align:middle; ">\(2.50\)	\ ({Pr}\)” style="text-align:center; vertical-align:middle; ">\(0.682\)
Ar	\ (\ eta\) (\(\mu{Pa}\cdot\Rs\))” style="text-align:center; vertical-align:middle; ">\(22.3\)	\ (\ kappa\) (\({mW}/\Rm\cdot\RK\))” style="text-align:center; vertical-align:middle; ">\(17.4\)	\ (c\ ns_p/\ kB\)” style="text-align:center; vertical-align:middle; ">\(2.50\)	\ ({Pr}\)” style="text-align:center; vertical-align:middle; ">\(0.666\)
Xe	\ (\ eta\) (\(\mu{Pa}\cdot\Rs\))” style="text-align:center; vertical-align:middle; ">\(22.7\)	\ (\ kappa\) (\({mW}/\Rm\cdot\RK\))” style="text-align:center; vertical-align:middle; ">\(5.46\)	\ (c\ ns_p/\ kB\)” style="text-align:center; vertical-align:middle; ">\(2.50\)	\ ({Pr}\)” style="text-align:center; vertical-align:middle; ">\(0.659\)
\(\RH\ns_2\)	\ (\ eta\) (\(\mu{Pa}\cdot\Rs\))” style="text-align:center; vertical-align:middle; ">\(8.67\)	\ (\ kappa\) (\({mW}/\Rm\cdot\RK\))” style="text-align:center; vertical-align:middle; ">\(179\)	\ (c\ ns_p/\ kB\)” style="text-align:center; vertical-align:middle; ">\(3.47\)	\ ({Pr}\)” style="text-align:center; vertical-align:middle; ">\(0.693\)
\(\RN\ns_2\)	\ (\ eta\) (\(\mu{Pa}\cdot\Rs\))” style="text-align:center; vertical-align:middle; ">\(17.6\)	\ (\ kappa\) (\({mW}/\Rm\cdot\RK\))” style="text-align:center; vertical-align:middle; ">\(25.5\)	\ (c\ ns_p/\ kB\)” style="text-align:center; vertical-align:middle; ">\(3.53\)	\ ({Pr}\)” style="text-align:center; vertical-align:middle; ">\(0.721\)
\(\RO\ns_2\)	\ (\ eta\) (\(\mu{Pa}\cdot\Rs\))” style="text-align:center; vertical-align:middle; ">\(20.3\)	\ (\ kappa\) (\({mW}/\Rm\cdot\RK\))” style="text-align:center; vertical-align:middle; ">\(26.0\)	\ (c\ ns_p/\ kB\)” style="text-align:center; vertical-align:middle; ">\(3.50\)	\ ({Pr}\)” style="text-align:center; vertical-align:middle; ">\(0.711\)
\(\RC\RH\ns_4\)	\ (\ eta\) (\(\mu{Pa}\cdot\Rs\))” style="text-align:center; vertical-align:middle; ">\(11.2\)	\ (\ kappa\) (\({mW}/\Rm\cdot\RK\))” style="text-align:center; vertical-align:middle; ">\(33.5\)	\ (c\ ns_p/\ kB\)” style="text-align:center; vertical-align:middle; ">\(4.29\)	\ ({Pr}\)” style="text-align:center; vertical-align:middle; ">\(0.74\)
\(\RC\RO\ns_2\)	\ (\ eta\) (\(\mu{Pa}\cdot\Rs\))” style="text-align:center; vertical-align:middle; ">\(14.8\)	\ (\ kappa\) (\({mW}/\Rm\cdot\RK\))” style="text-align:center; vertical-align:middle; ">\(18.1\)	\ (c\ ns_p/\ kB\)” style="text-align:center; vertical-align:middle; ">\(4.47\)	\ ({Pr}\)” style="text-align:center; vertical-align:middle; ">\(0.71\)
\(\RN\RH\ns_3\)	\ (\ eta\) (\(\mu{Pa}\cdot\Rs\))” style="text-align:center; vertical-align:middle; ">\(10.1\)	\ (\ kappa\) (\({mW}/\Rm\cdot\RK\))” style="text-align:center; vertical-align:middle; ">\(24.6\)	\ (c\ ns_p/\ kB\)” style="text-align:center; vertical-align:middle; ">\(4.50\)	\ ({Pr}\)” style="text-align:center; vertical-align:middle; ">\(0.90\)

Otra cantidad con dimensiones de\(L^2/T\) es la viscosidad cinemática,\(\nu=\eta/\rho\), donde\(\rho=nm\) está la densidad de masa. Se encontró\(\eta=n\kT\tau\) a partir del cálculo de aproximación del tiempo de relajación, por lo tanto\(\nu=\kT\tau/m\). La relación\(\nu/a\), llamada número Prandtl\({Pr}=\eta c\ns_p/m\kappa\), es adimensional. Según nuestros cálculos,\({Pr}=1\). Según la tabla [Prandtl], la mayoría de los gases monoatómicos tienen\({Pr}\approx\frac{2}{3}\).