3.4: Temperatura Absoluta y Entropía

Otra consecuencia de la segunda ley es la existencia de una temperatura absoluta. Aunque hemos utilizado la noción de temperatura absoluta, no fue probada. Ahora podemos mostrar esto solo desde las leyes de la termodinámica.

Ya hemos visto que la eficiencia de un ciclo Carnot viene dada por

\[η = 1 − \frac{Q_2}{Q_3}\]

donde\(Q_3\) es la cantidad de calor que se toma del reservorio más caliente y\(Q_2\) es la cantidad entregada al reservorio más frío. La eficiencia es independiente del material y es puramente una función de las temperaturas inferior y superior. Se puede tomar que el sistema en consideración esté en contacto térmico con los reservorios, los cuales pueden considerarse muy grandes. No hay intercambio de partículas ni ninguna otra cantidad física entre los reservorios y el sistema, por lo que ningún parámetro que no sea la temperatura puede desempeñar un papel en esto. Dejar\(θ\) denotar la temperatura empíricamente definida, con\(\theta_3\) y\(θ_2\) correspondientes a los depósitos entre los que está operando el motor. Así podemos escribir

\[\frac{Q_2}{Q_3} = f(θ_2, θ_3)\]

para alguna función\(f\) de las temperaturas. Ahora considere otro motor Carnot operando entre\(θ_2\) y\(θ_1\), con Q's correspondientes, para que tengamos

\[\frac{Q_1}{Q_2} = f(θ_1, θ_2)\]

Ahora podemos acoplar los dos motores y ejecutarlo juntos como un solo motor, operando entre\(θ_3\) y\(θ_1\), con

\[\frac{Q_1}{Q_3} = f(θ_1, θ_3)\]

Evidentemente

\[\frac{Q_2}{Q_3} \;\frac{Q_1}{Q_2} = \frac{Q_1}{Q_3}\]

para que consigamos la relación

\[f(θ_1, θ_2)\; f(θ_2, θ_3) = f(θ_1, θ_3)\]

Esto requiere que la función\(f\) debe ser de la forma

\[f(θ_1, θ_2) = \frac{f(θ_1)}{f(θ_2)}\]

para alguna función\(f(θ)\). Por lo tanto, debe existir alguna función de la temperatura empírica que pueda definirse independientemente del material. Esta temperatura se llama la temperatura absoluta. Observe que desde\(Q_1 < Q_2\), tenemos\(|f(θ_1)| < |f(θ_2)|\) si\(θ_1 < θ_2\). Por lo tanto,\(|f|\) debería ser una función creciente de la temperatura empírica. Además, no podemos tener\(f(θ_1) = 0\) para alguna temperatura\(θ_1\). Esto requeriría\(Q_1 = 0\). El motor correspondiente tomaría algo\(Q_2\) de calor del depósito más caliente y lo convertiría completamente a funcionar, contradiciendo la afirmación de Kelvin. Esto quiere decir que debemos tomar f para ser siempre positivos o siempre negativos, para todos\(θ\). Convencionalmente tomamos esto como positivo. La forma específica de la función determina la escala de temperatura. Lo más sencillo es tomar una función lineal de las temperaturas empíricas (definidas por los termómetros convencionales). Hoy, tomamos esto para ser

\[f(θ) ≡ T = \text{Temperature in Celsius} + 273.16\]

La unidad de temperatura absoluta es el kelvin.

Una vez definida la noción de temperatura absoluta, podemos simplificar la fórmula para la eficiencia del motor Carnot como

\[η = 1 − \frac{T_L}{T_H}\]

Figura\(\PageIndex{1}\): Ilustración del teorema de Clausius

También, tenemos\(\frac{Q1}{Q2} = \frac{T1}{T2}\), que podemos reescribir como\(\frac{Q1}{T1} = \frac{Q2}{T2}\). Dado que Q2 es el calor absorbido y Q1 es el calor liberado en el depósito, podemos asignar ± signos a las Q's, + para la entrada y − para la liberación de calor, y escribir esta ecuación como

\[\frac{Q_1}{T_1} + \frac{Q_2}{T_2} = 0\]

En otras palabras, si sumamos varios pasos (denotados por el índice i) del ciclo, con signos algebraicos apropiados,

\[\sum_{cycle} \frac{Q_i}{T_i} = 0 \label{3.4.11} \]

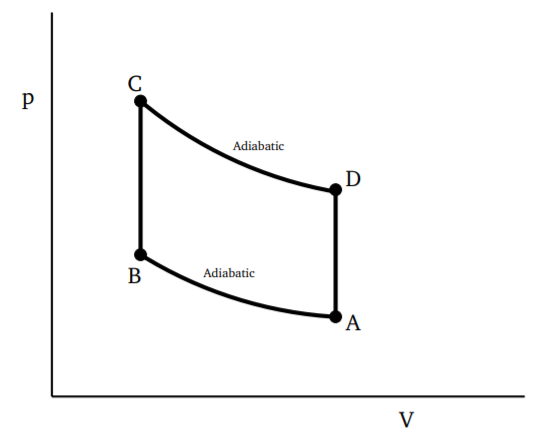
Si consideramos algún ciclo cerrado y reversible, como se muestra en la Fig. 3.4.1, podemos dividirlo en pequeños ciclos, cada uno de los cuales es un ciclo Carnot. Algunos de estos ciclos más pequeños se muestran mediante líneas punteadas, digamos con las líneas punteadas largas siendo adiabáticas y las líneas punteadas cortas siendo isotérmicas. Al tomar tales divisiones cada vez más finas, el error al aproximar el ciclo por una serie de ciclos cerrados de Carnot irá a cero ya que el número de ciclos de Carnot va al infinito. Dado que a lo largo de la adiabática, el cambio en\(Q\) es cero, podemos usar el resultado de la Ecuación\ ref {3.4.11} anterior para escribir

\[\oint_{cycle} \frac{dQ}{T}= 0 \label{3.4.12}\]

donde denotamos el calor absorbido o cedido durante cada paso infinitesimal como\(dQ\). La afirmación en la Ecuación\ ref {3.4.12} se debe a Clausius. Lo importante es que esto se aplique a cualquier curva cerrada en el espacio de las variables termodinámicas, siempre que el proceso sea reversible.

Esta ecuación tiene otra consecuencia muy importante. Si la integral de un diferencial alrededor de cualquier curva cerrada es cero, entonces podemos escribir el diferencial como la derivada de alguna función. Por lo tanto, debe existir una función\(S(p, V )\) tal que

\[\frac{dQ}{T} = dS,\;\;\; or\; dQ = TdS\]

Esta función\(S\) se llama entropía. Es una función de estado, dada en términos de las variables termodinámicas.

Desigualdad de Clausio

El descubrimiento de la entropía de Clausius es uno de los avances más importantes en la física de los sistemas materiales. Para un proceso reversible, tenemos el resultado,

\[\oint_{cycle} \frac{dQ}{T}= \oint_{cycle} dS = 0\]

como ya hemos visto. Hay un refinamiento adicional que podemos hacer considerando procesos irreversibles. Hay muchos procesos como la difusión que no son reversibles. Para tal proceso, no podemos escribir\(dQ = T dS\). Sin embargo, dado que la entropía es una función del estado del sistema, todavía podemos definir la entropía para cada estado. Para un proceso irreversible, el calor transferido a un sistema es menor que\(T dS\) donde\(dS\) está el cambio de entropía producido por el proceso irreversible. Esto se ve fácilmente desde la segunda ley. Por suponer que una cierta cantidad de calor\(dQ_{irr}\) es absorbida por el sistema en el proceso irreversible. Consideremos entonces un proceso combinado donde el sistema cambia del estado A al estado B de manera irreversible y luego restauramos el estado A mediante un proceso reversible. Para el último paso,\(dQ_{rev} = T dS\). La combinación absorbe así una cantidad de calor igual a\(dQ_{irr} −T dS\) sin cambio de estado. Si esto es positivo, éste debe ser totalmente convertido a trabajo. No obstante, eso violaría la segunda ley. De ahí que debamos tener

\[dQ_{irr} −T dS < 0\]

Si tenemos un proceso cíclico,\(\oint dS = 0\) ya que\(S\) es una función de estado, y por lo tanto

\[\oint \frac{dQ}{T} ≤ 0\]

con igualdad de retención para un proceso reversible. Esto se conoce como desigualdad de Clausio.

Para un sistema en aislamiento térmico,\(dQ = 0\), y la condición\(dQ_{irr} < T dS\) se convierte en

\[dS > 0\]

Es decir, la entropía de un sistema que se deja a sí mismo sólo puede aumentar, alcanzándose el equilibrio cuando la entropía (para los valores especificados de energía interna, número de partículas, etc.) es un máximo.

La segunda ley ha sido utilizada para definir la entropía. Pero una vez que hemos introducido la noción de entropía, la segunda ley equivale a la afirmación de que la entropía tiende a aumentar. Para cualquier proceso, podemos decir que

\[\frac{dS}{T} ≥ 0\]

En realidad podemos ver que esto equivale a la declaración Kelvin de la segunda ley de la siguiente manera. Considera un sistema que absorba calor\(∆Q\) a temperatura\(T\). Para el sistema (etiquetado 1) junto con la fuente de calor (etiquetada 2), tenemos\(∆S_1 + ∆S_2 ≥ 0\). Pero la fuente está perdiendo calor a temperatura\(T\) y si esto es reversible,\(∆S_2 = −\frac{∆Q}{T}\). Además si no hay otro cambio en el sistema,\(∆S_1 = 0\) y\(∆U_1 = 0\). Así

\[∆S_1 + ∆S_2 ≥ 0 \Rightarrow − \frac{∆Q}{T} ≥ 0 \Rightarrow ∆Q ≤ 0\]

Ya que\(∆U_1 = 0, ∆Q = ∆W\) y esta ecuación implica que el trabajo realizado por el sistema no puede ser positivo, si lo hemos hecho\(\frac{dS}{dt} ≥ 0\). Así, hemos llegado a la afirmación de Kelvin de que un sistema no puede absorber el calor de una fuente y convertirlo completamente para funcionar sin ningún otro cambio. Por lo tanto, podemos reafirmar la segunda ley en la forma:

Proposición 4

Segunda Ley de la Termodinámica: La entropía de un sistema que se deja a sí mismo tenderá a aumentar hasta un valor máximo compatible con los valores especificados de energía interna, número de partículas, etc.

Naturaleza del flujo de calor

Podemos ver fácilmente que el calor por sí mismo fluye de un cuerpo más caliente a un cuerpo más frío. Esto puede parecer obvio, pero es un resultado crucial de la segunda ley. De alguna manera, la segunda ley es la formalización de tales afirmaciones que son “obvias” desde nuestra experiencia.

Considerar dos cuerpos a temperaturas\(T_1\) y\(T_2\), aislados térmicamente del resto del universo pero en contacto térmico mutuo. Eso nos dice la segunda ley\(dS ≥ 0\). Esto significa que

\[\frac{dQ_1}{T1} + \frac{dQ_2}{T2}≥ 0\]

Porque los cuerpos están aislados del resto del mundo,\(dQ_1 + dQ_2 = 0\), para que podamos escribir la condición anterior como

\[(\frac{1}{T_1} − \frac{1}{T_2}) dQ_1 ≥ 0\]

Si\(T_1 > T_2\), debemos tener\(dQ_1 < 0\) y si\(T_1 < T_2, dQ_1 > 0\). De cualquier manera, el calor fluye del cuerpo más caliente al cuerpo más frío.

Figura\(\PageIndex{2}\): El ciclo Otto para un motor de automóvil.