8.4: Aplicaciones de la distribución Bose-Einstein

Ahora consideraremos algunas aplicaciones simples de la estadística cuántica, centrándonos en esta sección en la distribución de Bose-Einstein.

8.3.1: La distribución de Planck para la radiación del cuerpo negro

Cualquier cuerpo material a una temperatura finita distinta de cero emite radiación electromagnética, o fotones en el lenguaje de la teoría cuántica. Las características detalladas de esta radiación dependerán de la naturaleza de la fuente, su composición atómica, emisividad, etc. Sin embargo, si la fuente tiene una estructura suficientemente compleja, el espectro de radiación es esencialmente universal. Queremos derivar esta distribución universal, que también se conoce como la distribución de Planck.

Dado que un cuerpo negro absorbe toda la radiación que cae sobre él, tratando todas las longitudes de onda de la misma manera, un cuerpo negro puede ser tomado como un absorbedor perfecto. (Los cuerpos negros en realidad hacen esto sólo para una pequeña parte del espectro, pero aquí estamos considerando el caso idealizado). De la misma manera, los cuerpos negros también son emisores perfectos y de ahí que la fórmula para la radiación térmica universal se llame fórmula de radiación de cuerpo negro.

La fórmula de radiación de cuerpo negro fue obtenida por Max Planck ajustándose al espectro observado. También detalló algunos de los supuestos teóricos necesarios para derivar tal resultado y este fue, como es bien sabido, el inicio de la teoría cuántica. La derivación de Planck de esta fórmula es bastante simple una vez que se hacen ciertas suposiciones, radicales para su época; desde el punto de vista moderno es aún más simple. Los fotones son partículas de masa de reposo cero, la energía y el impulso de un fotón se dan como

\[\epsilon = ħ \omega , \;\;\;\;\; \vec{p} = ħ \vec{k} \label{8.3.1} \]

donde la frecuencia de la radiación\(ω\) y el número de onda\(\vec{k}\) están relacionados entre sí de la manera habitual,\(ω = c \; |\vec{k}|\). Además, los fotones son partículas de espina 1, por lo que sabemos que son bosones. Debido a que son sin masa, solo tienen dos estados de polarización, a pesar de que tienen giro igual a 1. (Para una partícula masiva debemos esperar estados de\((2 s + 1) = 3\) polarización para una partícula spin-1.) Podemos aplicar la ecuación de distribución Bose-Einstein 8.1.10 directamente, con una advertencia. El número de fotones no es un concepto bien definido. Dado que los fotones de longitud de onda larga llevan muy poca energía, el número de fotones para un estado de energía dada podría tener una ambigüedad de una gran cantidad de fotones suaves o de longitud de onda larga. Esto también se ve más teóricamente; no hay ley de conservación en la teoría electromagnética más allá de las habituales de energía e impulso. Esto significa que no debemos tener un potencial químico que se utilice para fijar el número de fotones. Así, la distribución de Bose-Einstein simplifica a

\[n = \frac{1}{e^{\beta \epsilon}-1} \]

Consideramos ahora una caja de volumen\(V\) en la que tenemos fotones en equilibrio térmico con partículas materiales como átomos y moléculas. La distribución de la energía interna en función del impulso viene dada por

\[dU = 2 \frac{d^3xd^3p}{(2 \pi ħ)^3} \frac{\epsilon}{e^{\beta \epsilon} - 1} \]

donde el factor de\(2\) es de los dos estados de polarización. Usando la ecuación\ ref {8.3.1}, para la densidad de energía, encontramos

\[d\;u = 2 \frac{d^3k}{(2 \pi)^3} \frac{ħ \omega}{e^{\frac{ħ \omega}{kT}} - 1} \label{8.3.4} \]

Esta es la fórmula de radiación de Planck. Si utilizamos\(ω = c \; |\vec{k}|\) y llevamos a cabo la integración sobre direcciones angulares de\(\vec{k}\), se reduce a

\[d\;u = \frac{ħ}{\pi^2 c^3} \frac{dω\;ω^3}{e^{\frac{ħω}{kT}} - 1} \label{8.3.5} \]

Esta función de distribución se desvanece en\(ω = 0\) y como\(ω → ∞\). Su pico alcanza un cierto valor que es una función de la temperatura. En la Fig. 8.3.1, se muestra la distribución para algunos valores de temperatura de muestra. Obsérvese que el valor de\(ω\) al máximo aumenta con la temperatura; además, la cantidad total de radiación (correspondiente al área bajo la curva) también aumenta con la temperatura.

Figura\(\PageIndex{1}\): La distribución de Planck en función de la frecuencia para tres valores muestrales de temperatura, con\(T_3 > T_2 > T_1\); las unidades son arbitrarias

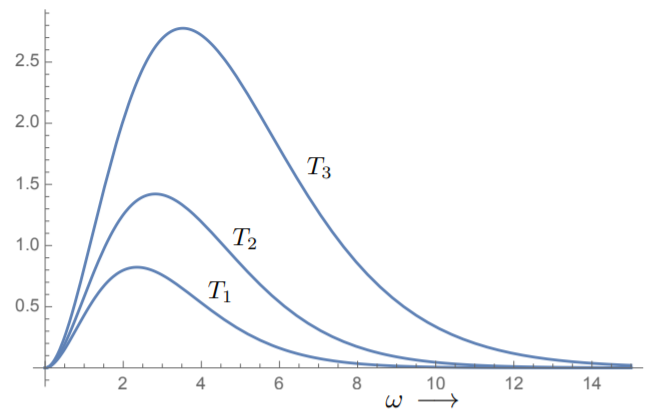
Si integramos\ ref {8.3.5} sobre todas las frecuencias, la densidad de energía total sale a ser

\[u = \frac{\pi^2}{15(ħc)^3}(kT)^4 \label{8.3.6} \]

donde hemos usado el resultado

\[\int_0^{\infty} dx \frac{x^3}{e^x - 1} = 3! \zeta(4) = \frac{\pi^4}{15} \]

Tasa de radiación de un cuerpo negro

Podemos convertir la fórmula para la densidad de energía a la intensidad de la radiación considerando la conservación de energía en la electrodinámica. La densidad de energía del campo electromagnético viene dada por

\[u = \frac{1}{2}(E^2 + B^2) \]

Usando las ecuaciones de Maxwell en el espacio libre, encontramos

\ [\ comenzar {ecuación}
\ comenzar {dividir}
\ frac {\ u parcial} {\ t parcial} & = e_i\ punto {E} _i + b_i\ punto {B} _i = c [e_I (\ nabla\ veces B) _i - b_i (\ nabla\ veces E) _i]\\ [0.125in]
& = -c\ nabla\ cdot (\ vec {E}\ veces\ vec {B}) = -\ nabla\ cdot\ vec {P}\\ [0.125 pulgadas]\ vec {P} & = c (\ vec {E}\ veces\ vec {B})
\ final {división}
\ final {ecuación}\]

Integrando sobre un volumen\(V\), encontramos

\[\frac{\partial}{\partial t} = \int d^3x\; u = \oint_{\partial V} \vec{P} \cdot d \vec{S} \]

Así, el flujo de energía por unidad de área o la intensidad viene dado por el vector Poynting\(\vec{P} = c (\vec{E} \times \vec{B})\). Para las ondas electromagnéticas\(|E| = |B|\),,\(\vec{E}\) y\(\vec{B}\) son ortogonales entre sí y ambas son ortogonales a\(\vec{k}\), el vector de onda que da la dirección de propagación, es decir, la dirección de propagación del fotón. En este caso encontramos

\[u = E^2,\;\;\;\;\vec{P} = cu\; \hat{k} \]

Usando la fórmula de Planck\ ref {8.3.4}, la magnitud de la intensidad de la radiación de cuerpo negro viene dada por

\[d\;I = 2c\frac{d^3k}{(2 \pi)^3} \frac{ħ \omega}{e^{\frac{ħ \omega}{kT}} - 1} \label{8.3.12}\]

Hemos considerado la radiación en una caja de volumen\(V\) en equilibrio. Para obtener la tasa de radiación por unidad de área de un cuerpo negro, tenga en cuenta que, debido al equilibrio, la tasa de radiación del cuerpo debe ser igual al flujo de energía que cae sobre el área en consideración (que se toma todo para ser absorbido ya que es un cuerpo negro); por lo tanto, la tasa de emisión es igual a la tasa de absorción como se esperaba para equilibrio. El flujo viene dado por

\[\vec{P} \cdot d \vec{S} = \vec{P} \cdot \hat{n}dS = cu \hat{k} \cdot \hat{n}dS = c u \cos \theta dS \]

donde\(\hat{n}\) es la normal a la superficie y\(θ\) es el ángulo entre\(\hat{k}\) y\(\hat{n}\). Además, en la situación de equilibrio, hay fotones que van y se alejan de la superficie bajo consideración, por lo que solo debemos considerar valores positivos de\(\hat{k} \cdot \hat{n} = \cos θ\), o\(0 ≤ θ ≤ \frac{π}{2}\). Por lo tanto, la tasa de radiación en todas las longitudes de onda por unidad de área del emisor viene dada por

\ [\ begin {ecuación}
\ begin {split}
R & = 2c\ int\ frac {d^3k} {(2\ pi) ^3}\ frac {\ omega cosθ} {e^ {\ frac {\ omega} {kT}} - 1}\\ [0.125in]
& = 2c\ int\ frac {dk\; k^2} {4\ pi^2}\ frac {\ omega} {e^ {\ frac {\ omega} {kT}} - 1}\ int_0^ {\ frac {\ pi} {2}} dθ\ sinθ\ cosθ\\ [0.125in ]
& =\ frac {} {4\ pi^2 c^2}\ int_0^ {\ infty} d\ omega\ frac {\ omega^3} {e^ {\ frac {\ omega} {kT}} - 1}\\ [0.125in]
& =\ sigma\; T^4\\ [0.125in]
\ sigma & =\ frac {pi^^2 k^4} {60h^3c^2}
\ end {split}
\ end {ecuación}\]

Este resultado se conoce como la ley Stefan-Boltzmann.

Presión de Radiación

Otro resultado interesante en relación con la radiación térmica es la presión de la radiación. Para ello, es conveniente utilizar una de las relaciones de la Ecuación 6.2.21, a saber,

\[\left( \frac{\partial U}{\partial V} \right)_T = T \left( \frac{\partial p}{\partial T} \right)_V - p \label{8.3.15}\]

De la Ecuación\ ref {8.3.6}, tenemos

\[U = V \frac{\pi^2}{15(ħc)^3} k^4 T^4 \label{8.3.16} \]

Las ecuaciones\ ref {8.3.15} y\ ref {8.3.16} conducen inmediatamente a

\[p = \frac{\pi^2}{45(ħc)^3} k^4 T^4 = \frac{1}{3}u \]

La presión de radiación es significativa e importante en astrofísica. Las estrellas se pueden ver como un gas o fluido que se mantienen unidos por gravedad. El gas tiene presión y el gradiente de presión entre el interior de la estrella y la región exterior tiende a crear una salida radial del material. Esto es contrarrestado por la gravedad que tiende a contraer o colapsar el material. El equilibrio hidrostático en la estrella se encuentra así entre los gradientes de gravedad y presión. La presión normal del fluido no es adecuada para evitar el colapso. La radiación producida por la fusión nuclear en el interior crea una presión externa y esto es un componente significativo en el equilibrio hidrostático de la estrella. Sin esta presión una estrella normal colapsaría rápidamente.

Máximo de distribución de Planck

Hemos visto que la distribución de Planck tiene un máximo a un cierto valor de\(ω\). Es interesante considerar la longitud de onda\(λ_∗\) a la que la distribución tiene un máximo. Esto se puede hacer en términos de frecuencia o longitud de onda, pero aquí usaremos la longitud de onda ya que esto es más apropiado para la aplicación que consideremos más adelante. (El pico de frecuencia y longitud de onda ocurre en diferentes lugares ya que estas variables no están linealmente relacionadas, sino que están recíprocamente relacionadas). Usando\(dω = −(2πc)\frac{dλ}{λ^2}\), podemos anotar la distribución de Planck (Ecuación\ ref {8.3.12}) en términos de la longitud de onda\(λ\) como

\[d\;I = \frac{2(2 \pi ħ)}{c^2} \frac{1}{λ^5 (e^{\frac{ħ \omega}{kT}} - 1)} dλ d \Omega \]

(El signo menos en\(dω\) solo sirve para mostrar que cuando la intensidad aumenta con la frecuencia, debe disminuir con\(λ\) y viceversa. Entonces hemos caído el signo menos. \(Ω\)es el ángulo sólido para las direcciones angulares.) Extremización con respecto a\(λ\) da la condición

\[(x-5)e^x + 5 = 0 \]

donde\(x = βħω\). La solución de esta ecuación trascendental es

\[λ_∗ \approx \frac{(2 \pi ħ)c}{k} \frac{1}{4.96511} \frac{1}{T} \label{8.3.20}\]

Esta relación es sumamente útil para determinar la temperatura de la capa externa de estrellas, llamada la fotosfera, de la que recibimos radiación. Al resolver espectroscópicamente la radiación y elaborar la distribución en función de la longitud de onda, podemos ver dónde está el máximo, y esto da, a través de la Ecuación\ ref {8.3.20}, la temperatura de la fotosfera. Observe que las temperaturas más altas corresponden a longitudes de onda más pequeñas; así las estrellas azules son más calientes que las rojas. Para el Sol, la temperatura de la fotosfera es aproximadamente\(5777 K\), correspondiente a una longitud de onda\(λ_∗ ≈ 502 nm\). Así, el máximo para la radiación del Sol se encuentra en la región visible, alrededor del color verde.

Otro caso de la importancia en la que la presión de radiación y la\(λ_∗\) que calculamos son importantes es en la historia temprana del universo. Poco después del Big Bang, el universo estaba en una fase muy caliente con todas las partículas teniendo una energía promedio tan alta que sus masas podían ser descuidadas. La presión de radiación de todas estas partículas, incluido el fotón, es un ingrediente importante para resolver las ecuaciones de Einstein para que la gravedad resuelva cómo se estaba expandiendo el universo. A medida que el universo se enfriaba por expansión, las partículas masivas inestables se desintegraron, ya que no había suficiente energía promedio en colisiones para sostener el proceso inverso. Los fotones continuaron dominando la evolución del universo. Esta fase del universo se conoce como la era dominada por la radiación.

Posteriormente, el universo se enfrió lo suficiente como para que los electrones y núcleos se combinaran para formar átomos neutros, una fase conocida como la era de la recombinación. Una vez que esto sucedió, dado que las partículas neutras se acoplan solo débilmente (a través de momentos dipolares y multipolares superiores) a la radiación, la radiación existente se desacopló y continuó enfriándose independientemente de la materia. Esta es la época dominada por la materia en la que ahora vivimos. La radiación obedeció al espectro de Planck en el momento de la recombinación, y aparte del enfriamiento continuaría haciéndolo en el universo en expansión. Así, la existencia de esta radiación reliquia de fondo es evidencia para la teoría del Big Bang. Esta radiación cósmica de fondo de microondas se predijo que sería una consecuencia de la teoría del Big Bang, por Gamow, Dicke y otros en la década de 1940. La temperatura fue estimada en cálculos por Alpher y Herman y por Gamow en las décadas de 1940 y 1950. La radiación fue observada por Penzias y Wilson en 1964. La temperatura de este fondo se puede medir de la misma manera que para las estrellas, comparando el máximo de la distribución con la fórmula\ ref {8.3.20}. Se encuentra que es aproximadamente\(2.7 K\). (En realidad esto ya se ha medido con gran precisión, siendo el último valor\(2.72548 ± 0.00057 K)\). El correspondiente\(λ_∗\) se encuentra en la región de microondas, razón por la cual a esto se le llama el fondo cósmico de microondas.

8.3.2: Condensación Bose-Einstein

Ahora trabajaremos algunas características de un gas ideal de bosones con un número de partículas conservadas; en este caso, sí tenemos un potencial químico. Hay muchos átomos que son bosones y, si podemos descuidar las fuerzas interatómicas como primera aproximación, esta discusión puede aplicarse a los gases hechos de tales átomos. La función de partición Z para gas de bosones se dio en la Ecuación 8.1.15. Dado que el log Z está relacionado con la presión como en la Ecuación 7.4.19, esto da inmediatamente

\ [\ begin {ecuación}
\ begin {split}
\ frac {pV} {kT} & =\ log Z = -\ int\ frac {d^3x d^3p} {(2\ pi) ^3\ log\ left (1-e^ {-\ beta (\ épsilon -\ mu)}\ derecha)}\\ [0.125in]
& = V\ izquierda (\ frac {MKt} {2\ pi ^2}\ derecha) ^ {\ frac {3} {2}}\ izquierda [z+\ frac {z^2} {2^\ frac {5} {2}} +\ frac { z^3} {3^\ frac {5} {2}} + · · ·\ derecha]\\ [0.125in]
& = V\ izquierda (\ frac {mKt} {2\ pi Ħ^2}\ derecha) ^ {\ frac {3} {2}}\ text {Li} _\ frac {5} {2} (z)\\ [0.125in]
\ fin {dividir}
\ final {ecuación}\ etiqueta {8.3.21}\]

donde\(z = e βµ\) es la fugacidad y\(\text{Li}_s(z)\) denota el polilogaritmo definido por

\[\text{Li}_s(z) = \sum_{n=1}^{\infty} \frac{z^n}{n^s} \]

El número total de partículas\(N\) viene dado por la condición de normalización (Ecuación 8.1.12) y funciona para

\ [\ begin {ecuación}
\ begin {split}
\ frac {N} {V} & =\ left (\ frac {mKt} {2\ pi Ħ^2}\ derecha) ^ {\ frac {3} {2}}\ izquierda [z+\ frac {z^2} {2^\ frac {3} {2}} +\ frac {z^3} {3^\ frac {3} {2}} + · · ·\ derecha]\\ [0.125in]
& =\ izquierda (\ frac {mKt} {2\ pi Ħ^2}\ derecha) ^ {\ frac {3} {2}}\ texto {Li} _\ frac {3} {2} (z) =\ frac {1} {λ^3}\ text {Li} _ {\ frac {3} {2} (z)}
\ end {split}
\ end {ecuación}\ label {8.3.23}\]

Hemos definido la longitud de onda térmica\(λ\) por

\[λ = \sqrt{\frac{2 \pi ħ^2}{mkT}} \]

Aparte de algunos factores numéricos de orden 1, esta es la longitud de onda de Broglie para una partícula de energía\(kT\).

Si\(z\) eliminamos a favor\(\frac{N}{V}\) de esta ecuación y la usamos en la Ecuación\ ref {8.3.21}, obtenemos la ecuación de estado para el gas ideal de bosones. Para altas temperaturas, esto se puede hacer manteniendo los términos\(z^2\) en orden en los polilogaritmos. Esto da

\[p = \frac{N}{V}kT \left[ 1- \frac{N}{V} \frac{λ^3}{2^{\frac{5}{2}}} + · · · \right] \]

Esta ecuación muestra que incluso el gas perfecto de bosones no sigue la ley clásica del gas ideal. De hecho, podemos leer el segundo coeficiente virial como

\[B_2 = - \frac{λ^3}{2^{\frac{5}{2}}} \label{8.3.26}\]

La longitud de onda térmica es pequeña para grande\(T\), por lo que esta corrección es pequeña a altas temperaturas, razón por la cual el gas ideal fue una buena aproximación para muchos de los primeros experimentos en física térmica. Si comparamos esto con el segundo coeficiente virial de un gas clásico con potencial interatómico\(V (x)\) dado en la Ecuación 7.5.11, es decir,

\[B_2 = \frac{1}{2} \int d^3x \left( 1- e^{- \beta V(x)} \right) \]

vemos que podemos imitar la Ecuación ref {8.3.26} por un atractivo potencial\( (V (x) < 0)\) interatómico. Así, los bosones muestran una tendencia a agruparse.

Ahora podemos considerar qué sucede cuando bajamos la temperatura. Es útil calcular un valor típico de\(λ\). Poniendo las constantes,

\[λ = \sqrt{\left( \frac{300}{T} \right) \left( \frac{m_p}{m} \right) } \times 6.3 \times 10^{-10} \text{ meters} \label{8.3.28}\]

(\(m_p\)es la masa del protón\(≈\) la masa del átomo de hidrógeno.) Así, para el hidrógeno a temperatura ambiente,\(λ\) es de tamaño atómico. Dado que\(\frac{V}{N}\) es aproximadamente el volumen libre disponible para una molécula, encontramos a partir de la Ecuación\ ref {8.3.23} que\(z\) debe ser muy pequeño en condiciones normales. La función\(Li_{\frac{3}{2}} (z)\) comienza desde cero en\(z = 0\) y se eleva a aproximadamente 2.61238 en\(z = 1\), ver Fig. 8.3.2. Más allá de eso, aunque la función pueda definirse por la continuación analítica, es imaginaria. De hecho, hay una rama cortada de\(z = 1\) a\(∞\). Así para\(z < 1\), podemos resolver la Ecuación\ ref {8.3.23} para\(z\) en términos de\(\frac{N}{V}\). A medida que se baja la temperatura,\(λ\) disminuye y eventualmente llegamos al punto donde\(z = 1\). Esto sucede a una temperatura

\[T_c = \frac{1}{k} \left( \frac{N}{V\;2.61238} \right)^{\frac{2}{3}} \left( \frac{2 \pi ħ^2}{m} \right) \label{8.3.29} \]

Si bajamos más la temperatura, se vuelve imposible satisfacer la Ecuación\ ref {8.3.23}. Podemos ver el problema en\(z = 1\) más claramente considerando la función de partición, donde separamos la contribución debido al estado de energía cero,

\[Z = \frac{1}{1-z} \prod_{p \neq 0} \frac{1}{1-ze^{-\beta \epsilon_p}} \]

Vemos que la función de partición tiene una singularidad en\(z = 1\). Esto es indicativo de una transición de fase. El sistema evita la singularidad al tener un gran número de partículas haciendo una transición al estado de cero energía e impulso. Recordemos que el factor\(\frac{1}{(1 − z})\) puede ser visto como\(\sum_n z^n\), como una suma sobre diferentes números de ocupación posibles para el estado base. La idea aquí es que, en lugar de varios números de ocupación posibles para el estado base, lo que sucede a continuación\(T_c\) es que hay un cierto número de ocupación para el estado base, digamos,\(N_0\), de modo que la función de partición debería leer

\[Z = z^{N_0} \prod_{p \neq 0} \frac{1}{1-ze^{-\beta \epsilon_p}} \]

Así, en lugar de tener diferentes probabilidades para los números de ocupación para el estado fundamental, con probabilidades correspondientemente diferentes dadas por el factor Boltzmann, tenemos un solo estado cuántico multipartícula, con número de ocupación\(N_0\), para el estado fundamental. La condición de normalización Ecuación\ ref {8.3.23} se cambia a

\[\frac{N}{V} = \frac{N_0}{V} + \frac{1}{λ^3} \text{Li}_{\frac{3}{2}} (z) \label{8.3.32} \]

A continuación\(T_c\), esta ecuación se satisface\(z = 1\), con, y con\(N_0\) compensar el segundo término en el lado derecho a medida que\(λ\) aumenta. Esto significa que un número macroscópicamente grande de partículas tiene que estar en el estado fundamental. Esto se conoce como condensación de Bose-Einstein. En términos de\(T_c\), podemos reescribir la ecuación\ ref {8.3.32} como

\[\frac{N_0}{V} = \frac{N}{V} + \left[1 - \left( \frac{T}{T_C} \right)^{\frac{3}{2}} \right] \label{8.3.33} \]

lo que da la fracción de partículas que se encuentran en el estado fundamental.

Ya que\(z = 1\) para temperaturas por debajo\(T_c\), tenemos\(µ = 0\). Esto es entonces una reminiscencia del caso de los fotones donde no tenemos un número de partículas conservadas. El tratamiento adecuado de este efecto de condensación requiere la teoría cuántica de campos, utilizando el concepto de ruptura de simetría espontánea. En tal descripción, se verá que el número de partículas sigue siendo un operador conservado pero que el estado condensado no puede ser un estado propio del número de partículas.

Figura\(\PageIndex{2}\): El polilogaritmo\ text {Li} _ {\ frac {3} {2}} (z)

Figura\(\PageIndex{3}\): Comportamiento cualitativo del calor específico de un gas de bosones

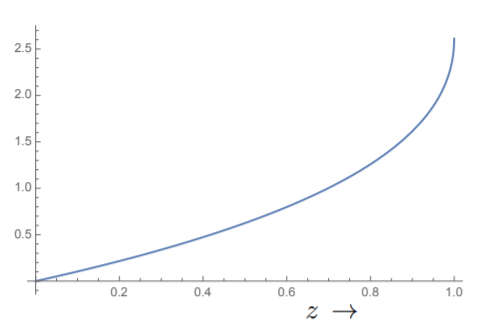
Hay muchas otras propiedades del fenómeno de condensación que podemos calcular. Aquí nos centraremos solo en el calor específico. La energía interna para el gas viene dada por

\ [\ begin {ecuación}
\ begin {split}
U & =\ int\ frac {d^3x d^3p} {(2\ pi) ^3}\ frac {\ épsilon} {e^ {\ beta (\ épsilon -\ mu)} - 1}\\ [0.125in]
& = V\ frac {3} {2} kT\ frac {1} λ^3}\ text {Li} _ {\ frac {5} {2}} (z)
\ end {split}
\ end {ecuación}\]

A altas temperaturas,\(z\) es pequeño y\( \text{Li}_{\frac{5}{2}} (z) ≈ z\) y la Ecuación\ ref {8.3.23} da\(\frac{z}{λ^3} = \frac{N}{V}\). Así,\(U = \frac{3}{2}N kT\) de acuerdo con el gas ideal clásico. Esto da\(C_v = \left( \frac{3}{2} \right) N k\).

Para bajas temperaturas por debajo\(T_c\),\(z = 1\) y podemos establecer\( \text{Li}_{\frac{5}{2}} (z) = \text{Li}_{\frac{5}{2}} (1) ≈ 1.3415\). El calor específico se convierte en

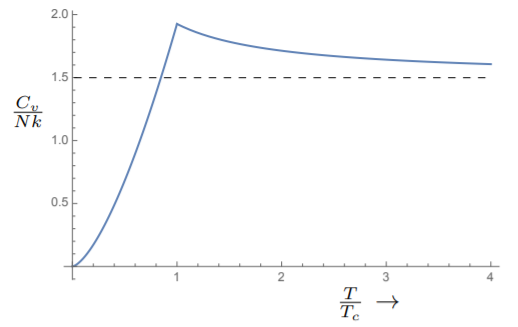
\[C_v = V\;k \frac{15}{4} \frac{ \text{Li}_{\frac{5}{2}} (1) }{λ^3} = N\;k \frac{15}{4} \frac{ \text{Li}_{\frac{5}{2}} (1) }{\text{Li}_{\frac{5}{2}} (1)} \left( \frac{T}{T_c} \right)^{\frac{3}{2}} ≈ 1.926\;N\;k\; \left( \frac{T}{T_c} \right)^{\frac{3}{2}} \]

Vemos que el calor específico va a cero a cero absoluto, de acuerdo con la tercera ley de la termodinámica. Se eleva a un valor que está algo por encima de\(\frac{3}{2}\) at\(T = T_c\). Arriba\(T_c\), debemos resolver para\(z\) en términos de\(N\) y sustituir de nuevo en la fórmula para\(U\). Pero cualitativamente, podemos ver que el calor específico tiene que disminuir para\(T > T_c\) alcanzar el valor de gas ideal de\(\frac{3}{2}\) a temperaturas muy altas. Una gráfica del calor específico se muestra en la Fig. 8.3.3.

Ya hay muchos ejemplos de condensación de Bose-Einstein. La fórmula para la longitud de onda térmica en la Ecuación\ ref {8.3.28} muestra que las masas atómicas más pequeñas tendrán mayores\(λ\) y se puede esperar que sufran condensación a temperaturas más altas. Si bien el hidrógeno molecular (que es un bosón) puede parecer el mejor candidato, se convierte en un sólido alrededor\(14 \;K\). El mejor candidato es así Helio líquido. Los átomos del isótopo\(\text{He}^4\) son bosones. El helio se convierte en un líquido por debajo\(4.2 K\) y tiene una densidad de aproximadamente\(125 \frac{kg}{m^3}\) (bajo presión atmosférica normal) y si este valor se usa en la fórmula\ ref {8.3.29}, encontramos\(T_c\) que se trata\(3\; K\). Lo que es notable es que el helio líquido sufre un cambio de fase en\(2.17\; K\). Por debajo de esta temperatura, se convierte en un superfluido, exhibiendo esencialmente viscosidad cero. (Los átomos He3 son fermiones, aquí también hay superfluidez, a una temperatura mucho menor, y el mecanismo es muy diferente). Esta transición puede considerarse como un ejemplo de condensación de Bose-Einstein. El helio no es un gas ideal de bosones, las fuerzas interatómicas (particularmente una repulsión de corto alcance) son importantes y esto puede explicar la discrepancia en el valor de\(T_c\). El calor específico del líquido\(\text{He}_4\) se muestra en la Fig. 8.3.4. Hay un punto de transición claro, con el calor específico mostrando una discontinuidad además del pico en este punto. Debido a la similitud de la gráfica con la letra griega\(λ\), esto a menudo se conoce como la\(λ\) transición. La gráfica es muy similar, en un sentido cualitativo amplio, al comportamiento que encontramos para la condensación de Bose-Einstein en la Fig. 8.3.3; sin embargo, la condensación de Bose-Einstein en el gas no interactuante es una transición de primer orden, mientras que la\(λ\) transición es una transición de segundo orden, por lo que hay diferencias con la condensación Bose-Einstein de gas perfecto de bosones.

Figura\(\PageIndex{4}\): Calor específico de helio líquido cerca\(λ\) de la transición

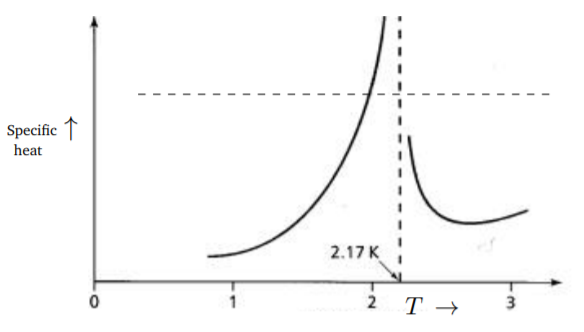
El tratamiento del helio superfluido a lo largo de las líneas que hemos utilizado para un gas perfecto es muy inadecuado. Un tratamiento más sofisticado tiene que tener en cuenta las fuerzas interatómicas e incorporar la idea de ruptura de simetría espontánea. A estas alturas, existe una teoría bastante completa del helio líquido.

Recientemente, la condensación de Bose-Einstein se ha logrado en muchos otros sistemas atómicos como un gas de\(\text{Rb}^87\) átomos,\(\text{Na}^23\) átomos y varios otros, en su mayoría elementos alcalinos y alcalinotérreos.

8.3.3: Calores Específicos de Sólidos

Pasamos ahora a los calores específicos de sólidos, siguiendo las líneas de trabajo que realizan Einstein y Debye. En un sólido, los átomos no son libres de moverse y por lo tanto no tenemos los habituales grados de libertad traslacionales. De ahí que la pregunta natural que se plantea es: Cuando se calienta un sólido, ¿cuáles son los grados de libertad en los que se puede almacenar la energía que se suministra? Como primera aproximación, los átomos en un sólido pueden tomarse para estar en los sitios de una red regular. Las fuerzas interatómicas mantienen cada átomo en su sitio, pero es posible cierta oscilación alrededor del sitio de la red. Esta es la dinámica detrás de la elasticidad del material. Estas oscilaciones, llamadas vibraciones de celosía, constituyen los grados de libertad que pueden ser excitados por la energía suministrada y, por lo tanto, son los agentes primarios para la capacidad calorífica específica de los sólidos. En un conductor, también es posible el movimiento traslacional de electrones. Por lo tanto, también hay una contribución electrónica al calor específico. Esto se retomará más adelante; aquí nos concentramos en el aporte de las vibraciones de celosía. En un sólido amorfo, no se obtiene una estructura reticular regular a lo largo del sólido, pero existen dominios con estructura regular, por lo que los modos elásticos de interés aún están presentes.

Figura\(\PageIndex{5}\): Curvas típicas de dispersión de fonones

Volviendo a los detalles de las vibraciones de la red, para los\(N\) átomos en una celosía, esperamos\(3N\) modos, ya que cada átomo puede oscilar a lo largo de cualquiera de las tres dimensiones. Dado que los átomos son como cuentas en una cuerda elástica, las oscilaciones se pueden transferir de un átomo al siguiente y así obtenemos ondas viajeras. Podemos caracterizarlos por una frecuencia ω y un número de onda\(\vec{k}\). La relación de dispersión entre\(ω\) y se\(\vec{k}\) puede obtener resolviendo las ecuaciones de movimiento para partículas\(N\) acopladas. Existen distintos modos correspondientes a diferentes\(ω-k\) relaciones; el comportamiento cualitativo típico se muestra en la Fig. 8.3.5. Existen tres modos acústicos para los cuales\(ω ≈ c_s|\vec{k}|\), para bajo\(|\vec{k}|\),\(c_s\) siendo la velocidad del sonido en el material. Las tres polarizaciones corresponden a oscilaciones en las tres direcciones posibles. La parte de longitud de onda larga de estos modos también se puede obtener resolviendo ondas elásticas (en términos de los módulos elásticos) en la aproximación continua a la red. Básicamente son ondas sonoras, de ahí el nombre de modos acústicos. El valor más alto para\(|\vec{k}|\) está limitado por el hecho de que realmente no tenemos un continuo; la longitud de onda más corta es del orden del espaciado de la red.

También están los llamados modos ópticos para los cuales\(ω \neq 0\) para cualquier\(\vec{k}\). La energía mínima necesaria para excitarlos se encuentra típicamente en el rango de 30-60 MeV más o menos; en términos de energía fotónica, ésta corresponde a las frecuencias ópticas infrarrojas y visibles, de ahí el nombre. Ya que\(1 \text{eV} ≈ 10^4 \;K\), los modos ópticos no son importantes para el calor específico a bajas temperaturas.

Así como las ondas electromagnéticas, tras la cuantificación, pueden verse como partículas, los fotones, las ondas elásticas en el sólido pueden describirse como partículas en la teoría cuántica. Estas partículas se llaman fonones y obedecen a las relaciones esperadas de energía e impulso

\[E = ħ \omega,\;\;\;\;\; \vec{p} = ħ \vec{k} \label{8.3.36}\]

La relación entre\(ω\) y\(\vec{k}\) puede aproximarse para los dos casos bastante bien por

\ [w\ approx\ begin {casos}
c_s |\ vec {k} | &\ text {(Acústico)}\\
\ omega_0 &\ text {(Óptico)}\\
\ end {casos}\]

donde\(ω_0\) es una constante independiente de\(\vec{k}\). Si hay varios modos ópticos, los correspondientes\(ω_0\) pueden ser diferentes. Aquí consideramos solo uno por simplicidad. Las polarizaciones corresponden a los tres ejes cartesianos y de ahí se transforman como vectores bajo rotaciones; es decir, tienen spin = 1 y por lo tanto son bosones. La termodinámica de estos ahora se puede elaborar fácilmente.

Primero, considere los modos acústicos. La energía interna total debida a estos modos es

\[ U = 3 \int \frac{d^3xd^3k}{(2 \pi )^3} \frac{ħ \omega}{e^{\beta ħ \omega} - 1} \]

El factor de 3 es para las tres polarizaciones. Para la mayor parte de la región de integración que contribuye significativamente, estamos considerando modos de longitudes de onda largas en comparación con el espaciado reticular y así podemos asumir la isotropía y llevar a cabo la integración angular. Para alto\(k\), la estructura cristalina específica y la anisotropía importarán, pero los correspondientes\(ω\) son altos y el\(e^{−βħω}\) factor disminuirá sus contribuciones a la integral. Así

\[ U = V \int \frac{3ħ}{2 \pi^2 c_{s}^3} \int_0^{\omega_D} d \omega \frac{\omega^3}{e^{\beta ħ \omega} - 1} \]

Aquí\(ω_D\) está la frecuencia de Debye que es la frecuencia más alta posible para los modos acústicos. El valor de esta frecuencia dependerá del sólido bajo consideración. También definimos una temperatura de Debye\(T_D\) por\(ħω_D\) =\(kT_D\). Luego encontramos

\[U = 3 \left( \frac{V}{2 \pi^2 ħ^3 c_{s}^3} \right) (kT)^4 \int_0^{\frac{T_D}{T}} du \frac{u^3}{e^u -1} \label{8.3.40} \]

Para bajas temperaturas,\(\frac{T_D}{T}\) es tan grande que se puede sustituir efectivamente por\(∞\) en una primera aproximación a la integral. Por alto\(T >> T_D\), podemos ampliar el integrando en poderes de u para llevar a cabo la integración. De esta manera encontramos

\ [\ int_0^ {\ frac {T_D} {T}} du\ frac {u^3} {e^u -1} =\ begin {casos}
\ frac {\ pi^4} {15} +\ mathcal {O} (e^ {-\ frac {T_D} {T}}) &\;\;\;\; << T_D\\
\ frac {1} {3}\ izquierda (\ frac {T_D} {T}\ derecha) ^3 -\ frac {1} {8}\ izquierda (\ frac {T_D} {T}\ derecha) ^4 + · · · &\;\;\;\;\;\;\;\; T>> T_D\\
\ end {casos}\]

La energía interna para\(T << T_D\) es así

\[U = \left( \frac{V}{2 \pi^2 ħ^3 c_{s}^3} \right) \frac{\pi^4 (kT)^4}{5} + \mathcal{O} (e^{-\frac{T_D}{T}}) \label{8.3.42}\]

El calor específico a bajas temperaturas es así dado por

\[U \approx \left( \frac{V}{2 \pi^2 ħ^3 c_{s}^3} \right) \frac{4\;k}{5} \pi^4 (kT)^3 \label{8.3.43} \]

Podemos relacionarlo con el número total de átomos en el material de la siguiente manera. Recordemos que el número total de modos vibracionales para los\(N\) átomos es\(3N\). Así

\[3 \int^{\omega_D} \frac{d^3x d^3k}{(2 \pi)^3} + \text{ Total number of optical modes} = 3N \]

Si ignoramos los modos ópticos, obtenemos

\[\left( \frac{V}{2 \pi^2 c_{s}^3} \right) = \frac{3N}{\omega_D^3} \]

Esta fórmula se mantendrá incluso con modos ópticos si\(N\) se interpreta como el número de celdas unitarias en lugar del número de átomos. En términos de\(N\), obtenemos, para\(T << T_D\),

\ [\ begin {ecuación}
\ begin {split}
U & =\ frac {3Nk\ pi^4} {5}\ frac {T^4} {T_D^3} +\ mathcal {O} (e^ {-\ frac {T_D} {T}})\\ [0.125in]
C_v & =\ frac {12Nk\ pi^4} {5}\ frac {T^3} {T_D^3} +\ mathcal {O} (e^ {-\ frac {T_D} {T}})
\ end {split}
\ end { ecuación}\ label {8.3.46}\]

La expresión para\(C_v\) en Ecuación\ ref {8.3.43} y\ ref {8.3.46} es la famosa\(T^3\) ley para calores específicos de sólidos a bajas temperaturas derivada por Debye en 1912. Hay una universalidad en ello. La derivación se basa únicamente en tener modos con\(ω ∼ k\) a bajo\(k\). Siempre hay tres modos de este tipo para cualquier sólido elástico. Estas son las ondas sonoras en el sólido. (La existencia de estos modos también se puede entender desde el punto de vista de la ruptura espontánea de la simetría, pero esa es otra cuestión.) El poder 3 está, por supuesto, relacionado con el hecho de que tenemos tres dimensiones espaciales. Por lo que cualquier sólido elástico exhibirá este comportamiento por la contribución de las vibraciones de la celosía. Como veremos en breve, los modos ópticos no alterarán este resultado. Algunos valores muestrales de la temperatura de Debye se dan en el Cuadro 8.3.1. Esto dará una idea de cuándo es aplicable la aproximación de baja temperatura.

Cuadro 8.3.1: Algunas temperaturas de Debye de la muestra
Sólido	\(T_D\)en\(K\)	Sólido	\(T_D\)en\(K\)
Oro	170	Aluminio	428
Plata	215	Hierro	470
Platino	240	Silicio	645
Cobre	343.5	Carbono	2230

Para\(T >> T_D\), encontramos

\ [\ begin {ecuación}
\ begin {split}
U & =\ left (\ frac {V} {2\ pi^2 c_ {s} ^3}\ derecha)\ izquierda [kT (\ Omega_d) ^4 -\ frac {3} {8} (\ Omega_d) ^3 +\ mathcal {O}\ left (\ frac {T_D} {T} derecha)\ derecha]\\ [0.125in]
& = 3N\ izquierda [kT -\ frac {3} {8}\ omega_D +\ mathcal {O}\ izquierda (\ frac {T_D} {T}\ derecha)\ derecha]
\ end {split}
\ end {ecuación}\ label {8.3.47}\]

El calor específico es entonces dado por

\[C_v = k \left( \frac{V}{2 \pi^2 c_{s}^3} \right) (ħ \omega_D)^3 + \mathcal{O}\left( \frac{1}{T^2} \right) = 3Nk + \mathcal{O}\left( \frac{1}{T^2} \right) \]

Pasando a los modos ópticos, observamos que la frecuencia\(ω\) es casi independiente de\(k\), para todo el rango de\(k\). Por lo que es una buena aproximación considerar solo una frecuencia\(ω_0\), para cada modo óptico. Dejar\(N_{opt}\) ser el número total de grados de libertad en el modo óptico de frecuencia\(ω_0\). Entonces la energía interna correspondiente viene dada por

\[U_{opt} = N_{opt} \frac{ħ \omega_0}{e^{\beta ħ \omega_0} - 1} \]

La contribución específica de calor viene dada por

\ [\ begin {ecuación}
\ begin {split}
U & = Nk\ frac {(\ beta\ omega_0) ^2} {(e^ {\ beta\ omega_0} - 1) (1 - e^ {\ beta\ omega_0})}\\ [0.125in]
&\ approx Nk\ left [1 -\ frac {1} {12}\ left (\ frac {1} {12}\ left (\ frac ac {\ omega_0} {kT}\ derecha) ^2 + · · ·\ derecha]\;\;\;\;\;\;\;\;\;\ texto {para} T > >\ omega_0\\ [0.125in] &\ approx Nk\ izquierda (\ frac {\ omega_0} {kT}\ derecha) ^2\;\ text {exp}\ left (-\ frac {\ omega_0} {kT}\ derecha)\;\;\;\;\;\;\;\;\\\\\ text {para} T <<\ omega_0
\ end {split}
\ end {ecuación}\ label {8.3.50}\]