2.6: Dos aplicaciones importantes

Los resultados de la sección anterior, especialmente la Ecuación (\(2.5.7\)), tienen innumerables aplicaciones en física y disciplinas afines, pero aquí tengo tiempo para una breve discusión de solo dos de ellas.

Radiación de cuerpo negro

Consideremos un volumen de espacio libre\(V\) limitado por paredes no absorbentes (es decir, idealmente reflectantes). La electrodinámica nos dice ⁴⁴ que el campo electromagnético en tal “cavidad” puede representarse como una suma de “modos” con la evolución temporal similar a la del oscilador armónico habitual. Si el volumen\(V\) es lo suficientemente grande, ⁴⁵ el número de estos modos dentro de un rango pequeño\(dk\) de la magnitud del evector de ondas\(k\) es

\[dN = \frac{gV}{(2\pi )^3} d^3k = \frac{gV}{(2\pi)^3} 4 \pi k^2 dk, \label{82}\]

donde para las ondas electromagnéticas, el factor de degeneración\(g\) es igual a 2, debido a sus dos diferentes polarizaciones independientes (e.g., lineales) de ondas con el mismo vector de onda\(k\). Con la relación de dispersión lineal e isotrópica para ondas en vacío,\(k = \omega /c\), Ecuación (\ ref {82}) rinde

\[dN = \frac{2V}{(2\pi )^3} 4\pi \frac{\omega^2 d \omega}{c^3} \equiv V \frac{\omega^2}{\pi^2 c^3} d \omega \label{83}\]

Por otro lado, la mecánica cuántica dice ⁴⁶ que la energía de tal “oscilador de campo” se cuantifica por la Ecuación (\(2.2.20\)), de manera que en el equilibrio térmico su energía promedio es descrita por la Ecuación (\(2.5.7\)). Conectando ese resultado a la Ecuación (\ ref {83}), vemos que la densidad espectral de la energía del campo electromagnético, por unidad de volumen, es

Ley de radiación de Planck:

\[\boxed{u(\omega) \equiv \frac{E}{V} \frac{dN}{d \omega} = \frac{\hbar \omega^3}{\pi^2 c^3} \frac{1}{e^{\hbar \omega / T} - 1} . } \label{84}\]

Esta es la famosa ley de radiación de cuerpo negro de Planck. ⁴⁷ Para entender por qué su nombre común menciona la radiación, consideremos una pequeña parte plana, de área\(dA\), de una superficie que absorbe completamente las ondas electromagnéticas incidentes desde cualquier dirección. (Tal aproximación de “cuerpo negro perfecto” puede ser abordada de cerca usando estructuras experimentales especiales, especialmente en intervalos de frecuencia limitados). La figura\(\PageIndex{1}\) muestra que si la onda que llega fuera plana, con el ángulo de incidencia\(\theta \), entonces la potencia\(d\mathscr{P}_{\theta} (\omega )\) absorbida por la superficie de área pequeña\(dA\), dentro de un pequeño intervalo de frecuencia\(d\omega \), es decir, la energía incidente en esa área en unidad de tiempo, sería igual a la radiación energía dentro del mismo intervalo de frecuencia, contenida dentro de un cilindro imaginario (sombreado en la Figura\(\PageIndex{1}\)) de altura\(c\), área base y\(dA \cos\theta \), por lo tanto, volumen\(dV = c dA \cos\theta \):

\[ d\mathscr{P}_{\theta} (\omega ) = u(\omega )d\omega dV = u(\omega )d\omega c dA \cos\theta . \label{85}\]

Figura\(\PageIndex{1}\): Cálculo de la relación
entre\(d\mathscr{P} (\omega )\) y\(u(\omega )d\omega \).

Dado que el campo inducido térmicamente es isotrópico, es decir, se propaga por igual en todas las direcciones, este resultado debe promediarse en todos los ángulos sólidos dentro del intervalo de ángulo polar\(0 \leq \theta \leq \pi /2\):

\[\frac{d \mathscr{P} ( \omega)}{dA d \omega} = \frac{1}{4\pi} \int \frac{d \mathscr{P} ( \omega)}{dA d \omega} d \Omega = cu (\omega ) \frac{1}{4\pi} \int^{\pi/2}_{0} \sin \theta d \theta \int^{2\pi }_{0} d \varphi \cos \theta = \frac{c}{4} u (\omega ). \label{86}\]

De ahí que la expresión de Planck (\ ref {84}), multiplicada por\(c/4\), da el poder absorbido por tal superficie de “cuerpo negro”. Pero en equilibrio térmico, esta absorción tiene que ser exactamente equilibrada por la propia radiación de la superficie, debido a su temperatura distinta de cero\(T\).

Espero que el lector esté familiarizado con las principales características de la ley Planck (\ ref {84}), incluyendo su forma general (Figura\(\PageIndex{2}\)), con la asíntota de baja frecuencia\(u(\omega ) \propto \omega^2\) (debido a su significación histórica que lleva el nombre especial de la ley Rayleigh-Jeans), la caída exponencial en alto frecuencias (la ley de Viena), y el máximo resultante de la función\(u(\omega )\), alcanzado a la frecuencia\(\omega_{max}\) con

\[\hbar \omega_{max} \approx 2.82 T, \label{87}\]

es decir, a la longitud de onda\(\lambda_{max} = 2\pi /k_{max} = 2 \pi c/\omega_{max} \approx 2.22 c\hbar /T\).

Figura\(\PageIndex{2}\): La dependencia de frecuencia de la densidad de radiación de cuerpo negro\(u_0 \equiv T^3/\pi^2\hbar^2c^3\), normalizada por, según la ley de Planck (línea roja) y la ley Rayleigh-Jeans (línea azul).

Aún así, no puedo dejar de mencionar algunos valores particulares importantes: uno correspondiente a la luz visible (\(\lambda_{max} \sim 500\)nm) para la temperatura superficial efectiva del Sol\(T_K \approx 6,000\) K, y otro correspondiente al rango del infrarrojo medio (\(\lambda_{max} \sim 10 \)\(\mu\)m) para la temperatura superficial de la Tierra\(T_K \approx 300\) K. El equilibrio de estas dos radiaciones, absorbidas y emitidas por la Tierra, determina su temperatura superficial y por lo tanto tiene la importancia clave para toda la vida en nuestro planeta. Es por ello que está al frente y centro de las discusiones actuales sobre el cambio climático. Como un ejemplo más, la radiación cósmica de fondo de microondas (CMB), siguiendo de cerca la ley de Planck con\(T_K = 2.725\) K (y por lo tanto teniendo la densidad máxima en\(\lambda_{max} \approx 1.9\) mm), y en particular su anisotropía (muy pequeña), es una fuente importante de datos para la cosmología moderna.

Ahora calculemos la energía total\(E\) de la radiación de cuerpo negro dentro de algún volumen\(V\). Se puede encontrar a partir de la Ecuación (\ ref {84}) por su integración en todas las frecuencias: ^48,49

\[ E = V \int^{\infty}_0 u (\omega ) d \omega = V \int^{\infty}_0 \frac{\hbar \omega^3}{\pi^2 c^3} \frac{d\omega}{e^{\hbar \omega /T} - 1} = \frac{VT^4}{\pi^2 \hbar^3 c^3} \int^{\infty}_0 \frac{\xi^3 d \xi}{e^{\xi} -1 } = V \frac{\pi^2}{15 \hbar^3 c^3} T^4. \label{88}\]

Ley de Stefan:

\[\boxed{ \frac{d\mathscr{P}}{dA} = \frac{\pi^2}{60\hbar^3 c^2} T^4 \equiv \sigma T^4_K , } \label{89a}\]

Constante de Stefan-Boltzmann:

\[\boxed{\sigma \equiv \frac{\pi^2}{60 \hbar^3 c^2} k^4_B \approx 5.67 \times 10^{-8} \frac{W}{m^2 K^4}. } \label{89b}\]

En este punto, el lector reflexivo debería tener lista una preocupación importante: La ecuación (\ ref {84}) y por lo tanto la ecuación (\ ref {88}) se basan en la ecuación (\(2.5.7\)) para la energía promedio de cada oscilador, referida a su energía de estado fundamental\(\hbar \omega /2\). Sin embargo, la potencia de radiación no debe depender del origen de la energía; ¿por qué no hemos incluido la energía terrestre de cada oscilador en la integración (\ ref {88}), como hemos hecho en la Ecuación (\(2.5.15\))? La respuesta es que los detectores de radiación habituales solo miden la diferencia entre la potencia\(\mathscr{P}_{in}\) de la radiación incidente (digamos, la de una superficie de cuerpo negro con temperatura\(T\)) y su propia potencia de retroradiación\(\mathscr{P}_{out}\), correspondiente a alguna temperatura efectiva\(T_d\) de el detector — ver Figura\(\PageIndex{3}\). Pero por muy baja\(T_d\) que sea, la contribución independiente de la temperatura\(\hbar \omega /2\) de la energía del estado fundamental a la radiación posterior siempre está ahí. De ahí que el término\(\hbar \omega /2\) baje de la balanza, y no se pueda detectar —al menos de esta manera sencilla. Esta es la razón por la que tuvimos derecho a ignorar esta contribución en la Ecuación (\ ref {88}) —muy afortunadamente, porque conduciría a la divergencia de la integral en su límite superior. No obstante, permítanme repetir que la energía del estado fundamental de los osciladores de campo electromagnético es físicamente real —e importante— véase la Sec. 5.5 a continuación.

Figura\(\PageIndex{3}\): El balance de potencia en la medición de la potencia de radiación electromagnética.

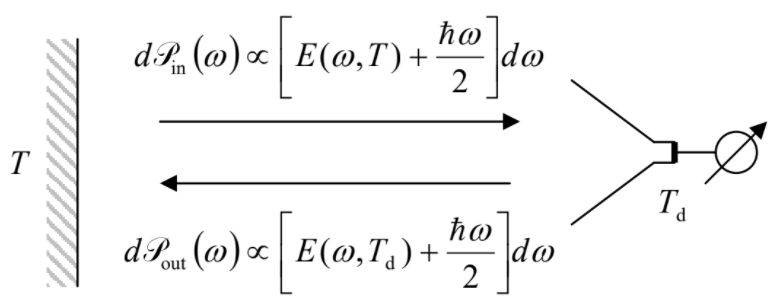
Un resultado más interesante puede deducirse de la energía libre\(F\) de la radiación electromagnética, que puede calcularse mediante la integración de la Ecuación (\(2.5.8\)) sobre todos los modos, con el peso apropiado (\ ref {83}):

\[F=\sum_{\omega} T \ln \left(1-e^{-\hbar \omega / T}\right) \rightarrow \int_{0}^{\infty} T \ln \left(1-e^{-\hbar \omega / T}\right) \frac{d N}{d \omega} d \omega=\int_{0}^{\infty} T \ln \left(1-e^{-\hbar \omega / T}\right)\left(V \frac{\omega^{2}}{\pi^{2} c^{3}}\right) d \omega. \label{90}\]

Representando\(\omega^2d\omega\) como\(d(\omega^3)/3\), podemos resolver fácilmente esta integral por partes, reduciéndola a una integral de tabla similar a la de la Ecuación (\ ref {88}), y obteniendo un resultado sorprendentemente simple:

\[F = -V \frac{\pi^2}{45 \hbar^3 c^3} T^4 \equiv - \frac{E}{3}. \label{91}\]

\[P = - \left( \frac{\partial F}{\partial V} \right)_T = \frac{ \pi^2}{45 \hbar^3 c^3} T^4 = \frac{E}{3V}. \label{92a}\]

Reescrito en la forma,

Gas fotón:\(\mathbf{PV}\) vs.\(\mathbf{E}\)

\[\boxed{ PV = \frac{E}{3},} \label{92b}\]

Por último, permítanme señalar que la Ecuación (\ ref {92a} -\ ref {92b}) permite la siguiente interpretación interesante. El último de las Eqs. (\(1.5.11\)), siendo aplicado a la Ecuación (\ ref {92a} -\ ref {92b}), muestra que en este caso particular el gran potencial termodinámico\(\Omega\) es igual\((–E/3)\), de manera que según la Ecuación (\ ref {91}), es igual a\(F\). Pero según la definición de\(\Omega \), es decir, la primera de las Eqs. (\(1.5.11\)), esto significa que el potencial químico de las excitaciones del campo electromagnético (fotones) desaparece:

\[\mu = \frac{F - \Omega}{N} = 0. \label{93}\]

En la Sec. 8 a continuación, veremos que el mismo resultado se desprende de la comparación de la Ecuación (\(2.5.7\)) y la distribución general de Bose-Einstein para bosones arbitrarios. Entonces, desde el punto de vista estadístico, los fotones pueden considerarse como bosones con potencial químico cero.

(ii) Calor específico de sólidos. La capacidad calorífica de los sólidos es fácilmente medible, y a principios del siglo XX, su dependencia experimentalmente observada de la temperatura sirvió como una prueba importante para las teorías cuánticas emergentes en ese momento. Sin embargo, el cálculo teórico de no\(C_V\) es simple ⁵³, incluso para aislantes, cuyo calor específico a temperaturas realistas se debe a las vibraciones inducidas térmicamente de su red cristalina sola. ⁵⁴ De hecho, a frecuencias relativamente bajas, un sólido puede ser tratado como un continuo elástico. Tal continuum soporta tres modos diferentes de ondas mecánicas con la misma frecuencia\(\omega \), que todos obedecen las leyes de dispersión lineal\(\omega = vk\), pero la velocidad\(v = v_l\) para uno de estos modos (el sonido longitudinal) es mayor que la\((v_t)\) de otros dos modos (el sonido transversal). ⁵⁵ A tales frecuencias, la densidad del modo de onda puede describirse mediante una generalización evidente de la Ecuación (\ ref {83}):

\[dN = V \frac{1}{(2\pi)^3} \left( \frac{1}{v^3_l} + \frac{2}{v^3_t} \right) 4 \pi \omega^2 d \omega. \label{94a}\]

Para lo que sigue, es conveniente reescribir esta relación en una forma similar a la Ecuación (\ ref {83}):

\[dN = \frac{3V}{(2\pi )^3} 4\pi \frac{\omega^2 d\omega}{v^3}, \quad \text{ with } v \equiv \left[ \frac{1}{3} \left( \frac{1}{v^3_l} + \frac{2}{v^3_t} \right) \right]^{-1/3}. \label{94b}\]

Sin embargo, la teoría básica de ondas muestra ⁵⁶ que a medida que aumenta la frecuencia\(\omega\) de una onda sonora en una estructura periódica de manera que su media longitud de onda se\(\pi /k\) acerca al período cristalino\(d\), la ley de dispersión\(\omega (k)\) se vuelve no lineal antes de que la frecuencia alcance su máximo en\(k = \pi /d\). Para hacer las cosas aún más complejas, los cristales 3D son generalmente anisotrópicos, por lo que la ley de dispersión es diferente en diferentes direcciones de la propagación de la onda. Como resultado, las estadísticas exactas de las ondas sonoras térmicamente excitadas, y de ahí la capacidad calorífica de los cristales, son bastante complejas y específicas para cada tipo de cristal en particular.

En 1912, P. Debye sugirió una teoría aproximada de la dependencia específica de la temperatura del calor, que está en un acuerdo sorprendentemente bueno con el experimento para muchos aislantes, incluyendo materiales policristalinos y amorfos. En su modelo, la ley de dispersión lineal (acústica)\(\omega = vk\), con la velocidad efectiva del sonido\(v\) definida por la segunda de Eqs. (\ ref {94b}), se supone que es exacto hasta alguna frecuencia de corte\(\omega_D\), lo mismo para los tres modos de onda. Esta frecuencia de Debye puede definirse por el requisito de que el número total de modos acústicos, calculado dentro de este modelo a partir de la Ecuación (\ ref {94b}),

\[N = V \frac{1}{(2\pi )^3} \frac{3}{v^3} \int^{\omega_D}_0 4 \pi \omega^2 d \omega = \frac{V \omega^3_D}{2\pi^2 v^3}, \label{95}\]

es igual al número universal\(N = 3nV\) de los grados de libertad (y por lo tanto de modos de oscilación independientes) en un sistema 3D de partículas acopladas\(nV\) elásticamente, donde\(n\) está la densidad atómica del cristal, es decir, el número de átomos por unidad de volumen. ⁵⁷ Para este modelo, la Ecuación (\(2.5.7\)) produce inmediatamente la siguiente expresión para la energía promedio y el calor específico (en equilibrio térmico a temperatura\(T \)):

\[E = V \frac{1}{(2\pi )^3} \frac{3}{v^3} \int^{\omega_D}_0 \frac{\hbar \omega}{e^{\hbar \omega /T}-1} 4 \pi \omega^2 d \omega \equiv 3 n VT D (x)_{x=T_D/T}, \label{96}\]

Ley Debye:

\[\boxed{c_V \equiv \frac{C_V}{nV} = \frac{1}{nV} \left( \frac{\partial E}{\partial T} \right)_V = 3 \left[ D(x) -x \frac{dD(x)}{dx} \right]_{x=T_D/T} , } \label{97}\]

donde\(T_D \equiv \hbar \omega_D\) se llama la temperatura de Debye, ⁵⁸ y

\[D(x) \equiv \frac{3}{x^{3}} \int_{0}^{x} \frac{\xi^{3} d \xi}{e^{\xi}-1} \rightarrow \begin{cases}1, & \text { for } x \rightarrow 0 , \\ \pi^{4} / 5 x^{3}, & \text { for } x \rightarrow \infty, \end{cases} \label{98}\]

es la función Debye. Las líneas rojas en la Figura\(\PageIndex{4}\) muestran la dependencia de la temperatura del calor específico\(c_V\) (por partícula) dentro del modelo de Debye. A altas temperaturas, se aproxima a un valor constante de tres, correspondiente a la energía\(E = 3nVT\), de acuerdo con el teorema de equipartición para cada uno de los tres grados de libertad (es decir, seis medios grados de libertad) de cada modo. (Este valor de\(c_V\) se conoce como la ley Dulong-Petit.) En el límite opuesto de bajas temperaturas, el calor específico es mucho menor:

\[c_V \approx \frac{12 \pi^4}{5} \left( \frac{T}{T_D} \right)^3 << 1, \label{99}\]

reflejando la reducción del número de fonones excitados con a\(\hbar \omega < T\) medida que disminuye la temperatura.

Figura\(\PageIndex{4}\): El calor específico en función de la temperatura en los modelos Debye (líneas rojas) y Einstein (líneas azules).

Como curiosidad histórica, la obra de P. Debye siguió una de A. Einstein, quien había sugerido (en 1907) un modelo más simple de vibraciones cristalinas. En su modelo, todos los modos oscilatorios\(3nV\) independientes de los\(nV\) átomos del cristal tienen aproximadamente la misma frecuencia, digamos\(\omega_E\), y la ecuación (\(2.5.7\)) inmediatamente rinde

\[E = 3nV \frac{\hbar \omega_E}{e^{\hbar \omega_E / T}-1}, \label{100}\]

para que el calor específico sea funcionalmente similar a la Ecuación (\(2.5.10\)):

\[c_V \equiv \frac{1}{nV} \left(\frac{\partial E}{\partial T}\right)_V =3 \left[ \frac{\hbar \omega_E / 2T}{\sinh ( \hbar \omega_E / 2T)} \right]^2. \label{101}\]

Esta dependencia\(c_V(T)\) se muestra con líneas azules en la Figura\(\PageIndex{4}\) (asumiendo, en aras de la simplicidad, eso\(\hbar \omega_E = T_D\)). A altas temperaturas, este resultado sí satisface la ley universal Dulong-Petit\((c_V = 3)\), pero para\(T << T_D\), el modelo de Einstein predice una caída mucho más rápida (exponencial) del corazón específico a medida que se reduce la temperatura. (La diferencia entre los modelos de Debye y Einstein no es demasiado espectacular en la escala lineal, pero en la gráfica logarítmica, mostrada en el panel derecho de Figura\(\PageIndex{4}\), es bastante dramática. ⁵⁹) El modelo de Debye está mucho mejor de acuerdo con los datos experimentales de cristales monoatómicos simples, confirmando así la corrección conceptual de su enfoque basado en ondas.

Tenga en cuenta, sin embargo, que cuando un genio como Albert Einstein comete un error, generalmente hay algunos antecedentes profundos e importantes debajo de él. De hecho, los cristales con la célula básica que consiste en átomos de dos o más tipos (como NaCl, etc.), presentan dos o más ramas separadas de la ley de dispersión\(\omega (k)\) — véase, por ejemplo, la Figura\(\PageIndex{5}\). Mientras que la rama inferior, “acústica” es prácticamente similar a las de los cristales monoatómicos y puede aproximarse por el modelo de Debye\(\omega = vk\), razonablemente bien, la rama superior (“óptica” ⁶⁰) no se acerca\(\omega = 0\) en ninguna\(k\). Además, para grandes valores de la relación de masa atómica\(r\), las ramas ópticas son casi planas, con frecuencias prácticamente\(k\) independientes\(\omega_0\), que corresponden a simples oscilaciones de cada átomo de luz entre sus vecinos pesados. Para las excitaciones térmicas de tales oscilaciones, y su contribución al calor específico, el modelo de Einstein (con\(\omega_E = \omega_0\)) da una muy buena aproximación, de manera que para tales sólidos, el calor específico puede ser bien descrito por una suma de las leyes de Debye y Einstein (\ ref {97}) y (\ ref {101}), con apropiadas pesos.

Figura\(\PageIndex{5}\): La relación de dispersión para ondas mecánicas en un modelo 1D simple de un sólido, con distancias interpartículas similares d, pero masas alternas de partículas, trazada para una relación de masa particular\(r = 5\) — ver CM Capítulo 6.