5.2: La energía y el número de partículas

En primer lugar, tenga en cuenta que las fluctuaciones de las variables macroscópicas dependen de condiciones particulares. ² Por ejemplo, en un sistema de aislamiento mecánico y térmico con un número fijo de partículas, es decir, un miembro de un conjunto microcanónico, la energía interna no fluctúa:\(\delta E = 0\). Sin embargo, si dicho sistema está en contacto térmico con el ambiente, es decir, es miembro de un conjunto canónico (Figura\(2.4.1\)), la situación es diferente. En efecto, para tal sistema podemos aplicar la Ecuación general (\(2.1.7\)), con\(W_m\) dada por la distribución de Gibbs (\(2.4.7\)) - (\(2.4.8\)), no sólo a\(E\) sino también a\(E^2\). Como ya sabemos por la Sec. 2.4, el primer promedio,

\[\langle E \rangle = \sum_m W_m E_m , \quad W_m = \frac{1}{Z} \exp \left\{ - \frac{E_m}{T}\right\}, \quad Z = \sum_m \exp \left\{- \frac{E_m}{T}\right\}, \label{15}\]

produce la ecuación (\(2.4.10\)), que puede ser reescrita en la forma

\[\langle E \rangle = \frac{1}{Z} \frac{\partial Z}{\partial (- \beta )}, \quad \text{ where } \beta \equiv \frac{1}{T}, \label{16}\]

más conveniente para nuestros propósitos actuales. Realicemos un cálculo similar para\(E^2\):

\[\langle E^2 \rangle = \sum_m W_m E^2_m = \frac{1}{Z} \sum_m E^2_m \exp \{-\beta E_m \}. \label{17}\]

Es sencillo verificar, por doble diferenciación, que la última expresión pueda ser reescrita en una forma similar a la Ecuación (\ ref {16}):

\[\left\langle E^{2}\right\rangle=\frac{1}{Z} \frac{\partial^{2}}{\partial(-\beta)^{2}} \sum_{m} \exp \left\{-\beta E_{m}\right\} \equiv \frac{1}{Z} \frac{\partial^{2} Z}{\partial(-\beta)^{2}} . \label{18}\]

Ahora es fácil de usar Eqs. (\(5.1.4-5.1.5\)) para calcular la varianza de las fluctuaciones de energía:

\[\left\langle\widetilde{E}^{2}\right\rangle=\left\langle E^{2}\right\rangle-\langle E\rangle^{2}=\frac{1}{Z} \frac{\partial^{2} Z}{\partial(-\beta)^{2}}-\left(\frac{1}{Z} \frac{\partial Z}{\partial(-\beta)}\right)^{2} \equiv \frac{\partial}{\partial(-\beta)}\left(\frac{1}{Z} \frac{\partial Z}{\partial(-\beta)}\right)=\frac{\partial\langle E\rangle}{\partial(-\beta)}. \label{19}\]

Desde Eqs. (\ ref {15}) - (\ ref {19}) son válidos solo si el volumen del sistema\(V\) es fijo (porque su cambio puede afectar el espectro de energía\(E_m\)), es costumbre reescribir este importante resultado de la siguiente manera:

Fluctuaciones de\(E\):

\[\boxed{ \langle \tilde{E}^2 \rangle = \frac{\partial \langle E \rangle}{\partial (-1 / T) } = T^2 \left( \frac{\partial \langle E \rangle}{\partial T } \right)_V \equiv C_V T^2 . } \label{20}\]

Este es un resultado notablemente simple y fundamental. Como un chequeo de cordura, para un sistema de partículas\(N\) similares, independientes,\(\langle E \rangle\) y por lo tanto\(C_V\) son proporcionales a\(N\), de manera que\(\delta E \propto N^{1/2}\) y\(\delta E/\langle E\rangle \propto N^{–1/2}\), de acuerdo con la Ecuación (\(5.1.13\)). Permítanme enfatizar que la Ecuación de aspecto clásico (\ ref {20}) se basa en la distribución general de Gibbs, y por lo tanto es válida para cualquier sistema (ya sea clásico o cuántico) en equilibrio térmico.

Algunos corolarios de este resultado serán discutidos en la siguiente sección, y ahora vamos a llevar a cabo un cálculo muy similar para un sistema cuyo número\(N\) de partículas en un sistema no es fijo, porque pueden ir a, y venir de su entorno a voluntad. Si el potencial químico\(\mu\) del ambiente y su temperatura\(T\) son fijos, es decir, estamos tratando con el gran conjunto canónico (Figura\(2.7.1\)), podemos usar la gran distribución canónica (\(2.7.5\)) - (\(2.7.6\)):

\[W_{m,N} = \frac{1}{Z_G} \exp \left\{\frac{\mu N - E_{m,N}}{T}\right\}, \quad Z_G = \sum_{N,m} \exp \left\{\frac{\mu N - E_{m,N}}{T}\right\}. \label{21}\]

Actuando exactamente como lo hicimos anteriormente para la energía interna, obtenemos

\[\langle N \rangle = \frac{1}{Z_G} \sum_{m,N} N \exp \left\{\frac{\mu N - E_{m,N}}{T}\right\} = \frac{T}{Z_G} \frac{\partial Z_G}{\partial \mu }, \label{22}\]

\[\langle N^2 \rangle = \frac{1}{Z_G} \sum_{m,N} N^2 \exp \left\{\frac{\mu N - E_{m,N}}{T}\right\} = \frac{T^2}{Z_G} \frac{\partial^2 Z_G}{\partial \mu^2 }, \label{23}\]

de manera que la varianza del número de partículas sea

Fluctuaciones de\(N\):

\[\boxed{ \left\langle\widetilde{N}^{2}\right\rangle=\left\langle N^{2}\right\rangle-\langle N\rangle^{2}=\frac{T^{2}}{Z_{G}} \frac{\partial Z_{G}}{\partial \mu}-\frac{T^{2}}{Z_{G}^{2}}\left(\frac{\partial Z_{G}}{\partial \mu}\right)^{2}=T \frac{\partial}{\partial \mu}\left(\frac{T}{Z_{G}} \frac{\partial Z_{G}}{\partial \mu}\right)=T \frac{\partial\langle N\rangle}{\partial \mu}, } \label{24}\]

en completa analogía con la Ecuación (\ ref {19}).

En particular, para un gas clásico ideal, podemos combinar el último resultado con la ecuación (\(3.2.2\)). (Como ya se enfatizó en la Sec. 3.2, aunque ese resultado se ha obtenido para el conjunto canónico, en el que\(N\) se fija el número de partículas, a\(N >> 1\) las fluctuaciones de\(N\) en el gran conjunto canónico debe ser relativamente pequeño, por lo que la misma relación debería ser válida para el promedio\(\langle N\rangle\) en ese conjunto.) Fácilmente resolviendo la ecuación (\(3.2.2\)) para\(\langle N\rangle \), obtenemos

\[\langle N \rangle = \text{const} \times \exp \left\{\frac{\mu}{T}\right\}, \label{25}\]

donde “const” significa una constante de factor en la diferenciación parcial de\(\langle N \rangle\) over\(\mu \), requerida por la Ecuación (\ ref {24}). Realizando la diferenciación y luego usando de nuevo la Ecuación (\ ref {25}),

\[\frac{\partial \langle N \rangle }{\partial \mu } = \text{const} \times \frac{1}{T} \exp \left\{\frac{\mu}{T}\right\} = \frac{\langle N \rangle }{T}, \label{26}\]

obtenemos de Ecuación (\ ref {24}) un resultado muy simple:

Fluctuaciones de\(N\): gas clásico

\[\boxed{ \langle \tilde{N}^2 \rangle = \langle N \rangle, \quad \text{ i.e. } \delta N = \langle N \rangle^{1/2} . } \label{27}\]

Esta relación es tan importante que también voy a mostrar cómo se puede derivar de manera diferente. Como subproducto de esta nueva derivación, demostraremos que este resultado es válido para sistemas con una arbitraria (digamos, pequeña)\(N\), y además obtendremos información más detallada sobre las estadísticas de fluctuaciones de ese número. Consideremos un gas clásico ideal de\(N_0\) partículas en un volumen\(V_0\), y calculemos la probabilidad de\(W_N\) tener exactamente\(N \leq N_0\) de estas partículas en su parte de volumen\(V \leq V_0\) — ver Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Derivando las distribuciones binomiales y de Poisson.

Para una partícula tal probabilidad es\(W = V/V_0 = \langle N\rangle /N_0 \leq 1\), mientras que la probabilidad de tener esa partícula en la parte restante del volumen es\(W' = 1 – W = 1 – \langle N\rangle /N_0\). Si todas las partículas fueran distinguibles, la probabilidad de tener partículas\(N \leq N_0\) específicas en volumen\(V\) y partículas\((N – N_0)\) específicas en volumen\((V – V_0)\), sería\(W^NW^{\prime (N_0-N)}\). Sin embargo, si no queremos distinguir las partículas, debemos multiplicar esta probabilidad por el número de posibles combinaciones de partículas manteniendo los números\(N\) y\(N_0\) constantes, es decir, por el coeficiente binomial\(N_0!/N!(N_0 – N)!\). ³ Como resultado, la probabilidad requerida es

Distribución binomial:

\[\boxed{W_N = W^N W^{'(N_0-N)} \frac{N_0!}{N!(N_0 - N)!} = \left(\frac{\langle N \rangle }{N_0} \right)^N \left(1-\frac{\langle N\rangle}{N_0}\right)^{N_0-N} \frac{N_0!}{N!(N_0 - N)!}. } \label{28}\]

Esta es la denominada distribución binomial de probabilidad, válida para cualquier\(\langle N\rangle\) y\(N_0\). ⁴

Aún\(\langle N\rangle\) manteniéndonos arbitrarios, podemos simplificar la distribución binomial asumiendo que todo el volumen\(V_0\), y por lo tanto\(N_0\), son muy grandes:

\[ N_0 >> N , \label{29}\]

donde\(N\) significa todos los valores de interés, incluyendo\(\langle N\rangle \). En efecto, en este límite podemos descuidar\(N\) en comparación con\(N_0\) en el segundo exponente de la Ecuación (\ ref {28}), y también aproximar la fracción\(N_0!/(N_0 – N)!\), es decir, el producto de\(N\) términos\((N_0 – N + 1) (N_0 – N + 2)...(N_0 – 1)N_0\),, por solo\(N_0^N\). Como resultado, obtenemos

\[W_N \approx \left( \frac{\langle N \rangle}{N_0 } \right)^N \left( 1 - \frac{\langle N \rangle}{N_0 } \right)^{N_0} \frac{N_0^N}{N!} \equiv \frac{\langle N \rangle^N}{N! } \left(1 - \frac{\langle N \rangle}{N_0 } \right)^{N_0} = \frac{\langle N \rangle^N}{N! } \left[ (1-W)^{\frac{1}{W}} \right]^{\langle N \rangle } , \label{30}\]

donde, como antes,\(W = \langle N\rangle /N_0\). En el límite (\ ref {29})\(W \rightarrow 0\), de manera que el factor dentro de los corchetes tiende a\(1/e\), el recíproco de la base logaritmo natural. ⁵ Así, obtenemos una expresión independiente de\(N_0\):

Distribución de Poisson:

\[\boxed{ W_N = \frac{\langle N \rangle^N}{N!} e^{-\langle N \rangle }. } \label{31}\]

Esta es la tan célebre distribución de Poisson ⁶ que describe una familia muy amplia de fenómenos aleatorios. La figura\(\PageIndex{2}\) muestra esta distribución para varios valores de\(\langle N\rangle\) — que, en contraste con\(N\), no son necesariamente enteros.

Figura\(\PageIndex{2}\): La distribución de Poisson para varios valores de\(\langle N\rangle \). A diferencia de ese promedio, el argumento\(N\) puede tomar solo valores enteros, de manera que las líneas en estas gráficas son solo guías para el cyc.

Distribución gaussiana:

\[\boxed{W_N = \frac{1}{(2\pi )^{1/2} \delta N} \exp \left\{ - \frac{(N - \langle N \rangle )^2}{2(\delta N )^2 } \right\} . } \label{32}\]

(Tenga en cuenta que la distribución gaussiana también es válida si ambos\(N\) y\(N_0\) son grandes, independientemente de la relación entre ellos — ver Figura\(\PageIndex{3}\).)

Figura\(\PageIndex{3}\): La jerarquía de tres distribuciones de probabilidad principales.

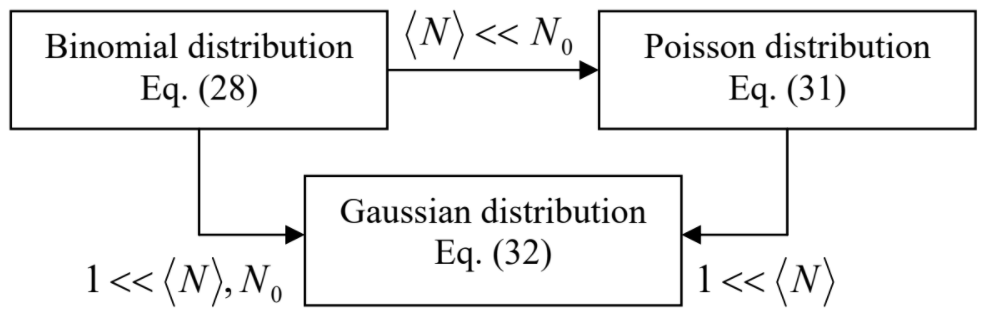
Una propiedad importante de la distribución de Poisson (y por lo tanto de la gaussiana) es que tiene la misma varianza dada por la ecuación (\ ref {27}):

\[\langle \tilde{N}^2 \rangle \equiv \left\langle ( N - \langle N \rangle )^2 \right\rangle = \langle N \rangle . \label{33}\]

(Esto no es cierto para la distribución binomial general.) Para nuestros propósitos actuales, esto significa que para el gas clásico ideal, la Ecuación (\ ref {27}) es válida para cualquier número de partículas.