6.3: Potencial electroquímico y ecuación de difusión-deriva

Ahora generalicemos nuestro cálculo al caso en que el transporte de partículas tiene lugar en presencia de un gradiente espacial independiente del tiempo de la distribución de probabilidad\(\nabla_rw \neq 0\), causado por ejemplo por el de la concentración de partículas\(n = N/V\) (y por lo tanto, según la Ecuación (\(3.2.11\)), de el potencial químico\(\mu \)), sin dejar de asumir que la temperatura\(T\) es constante. Para esta generalización, debemos mantener el segundo término en el lado izquierdo de la Ecuación (\(6.1.18\)). Si el gradiente de\(w\) es suficientemente pequeño, podemos repetir los argumentos de la última sección y\(w\) reemplazarlos con\(w_0\) en este término también. Con el campo eléctrico aplicado\(\pmb{\mathscr{E}}\) representado como\((–\nabla \phi )\), ²¹ donde\(\phi\) está el potencial electrostático, la ecuación (\(6.2.7\)) se convierte

\[\tilde{w} = \tau \mathbf{v} \cdot \left( \frac{\partial w_0}{\partial \varepsilon} q \nabla \phi - \nabla w_0 \right). \label{36}\]

Dado que en cualquiera de las distribuciones de equilibrio (\(6.2.2\)),\(\langle N(\varepsilon )\rangle\) es una función de\(\varepsilon\) y\(\mu\) solo en la combinación\((\varepsilon – \mu )\), obedece a la siguiente relación:

\[\frac{\partial \langle N (\varepsilon ) \rangle}{\partial \mu } = - \frac{\partial \langle N (\varepsilon ) \rangle }{\partial \varepsilon}.\label{37}\]

\[\nabla w_0 = - \frac{\partial w_0}{\partial \varepsilon } \nabla \mu, \quad \text{ for } T = \text{ const}, \label{38}\]

para que la Ecuación (\ ref {36}) se convierta

\[\tilde{w} = \tau \frac{\partial w_0}{\partial \varepsilon} \mathbf{V} \cdot ( q \nabla \phi + \nabla \mu ) \equiv \tau \frac{\partial w_0}{\partial \varepsilon} \mathbf{v} \cdot \nabla \mu ' , \label{39}\]

donde la siguiente suma,

Potencial electroquímico:

\[\boxed{\mu ' \equiv \mu + q \phi , } \label{40}\]

se llama el potencial electroquímico. Ahora repitiendo el cálculo de la corriente eléctrica, realizado en el último apartado, obtenemos la siguiente generalización de la ley Ohm (\(6.2.10\)):

\[\mathbf{j} = \sigma (− \nabla \mu ' / q) \equiv \sigma \mathcal{E} , \label{41}\]

donde el campo eléctrico efectivo\(\mathcal{E}\) es proporcional al gradiente del potencial electroquímico, más bien del potencial electrostático:

Campo eléctrico efectivo:

\[\boxed{ \mathcal{E} \equiv - \frac{\nabla \mu '}{q} = \pmb{\mathscr{E}} - \frac{\nabla \mu}{q} .} \label{42}\]

La física de este resultado sumamente importante y general ²³ puede explicarse de dos maneras. Primero, echemos un vistazo al espectro energético de un gas Fermi degenerado confinado en un volumen de tamaño finito, pero por lo demás libre. Para asegurar tal confinamiento necesitamos un potencial constante por partes, un “pozo de potencial\(U(\mathbf{r})\) de pared dura y fondo plano”, ver Figura\(\PageIndex{1a}\). (Para los electrones de conducción en un metal, dicho perfil es proporcionado por los iones cargados positivamente de la red cristalina). El pozo debe ser de una profundidad suficiente\(U_0 > \varepsilon_F \equiv \mu |_{T = 0}\) para proporcionar el confinamiento de la abrumadora mayoría de las partículas, con energías por debajo y algo por encima del nivel Fermi\(\varepsilon_F\). Esto significa que debe haber una brecha energética sustancial,

\[ \Psi \equiv U_0 − \mu >> T , \label{43}\]

entre la energía Fermi de una partícula dentro del pozo, y su energía potencial\(U_0\) fuera del pozo. (Este último valor de la energía se suele llamar el nivel de vacío). La diferencia definida por la Ecuación (\ ref {43}) se llama función de trabajo; ²⁴ para la mayoría de los metales, está entre 4 y 5 eV, de manera que la relación\(\Psi >> T\) se cumple bien para las temperaturas ambiente (\(T \sim 0.025\)eV) —y en realidad para todas las temperaturas hasta el punto de evaporación del metal.

Figura\(\PageIndex{1}\): Perfiles potenciales de (a) un solo conductor y (b, c) un sistema de dos conductores ubicados cerca, para dos situaciones de polarización diferentes: (b) campo electrostático cero (la “condición de banda plana”) y (c) voltaje cero\(\Delta \mu '\).

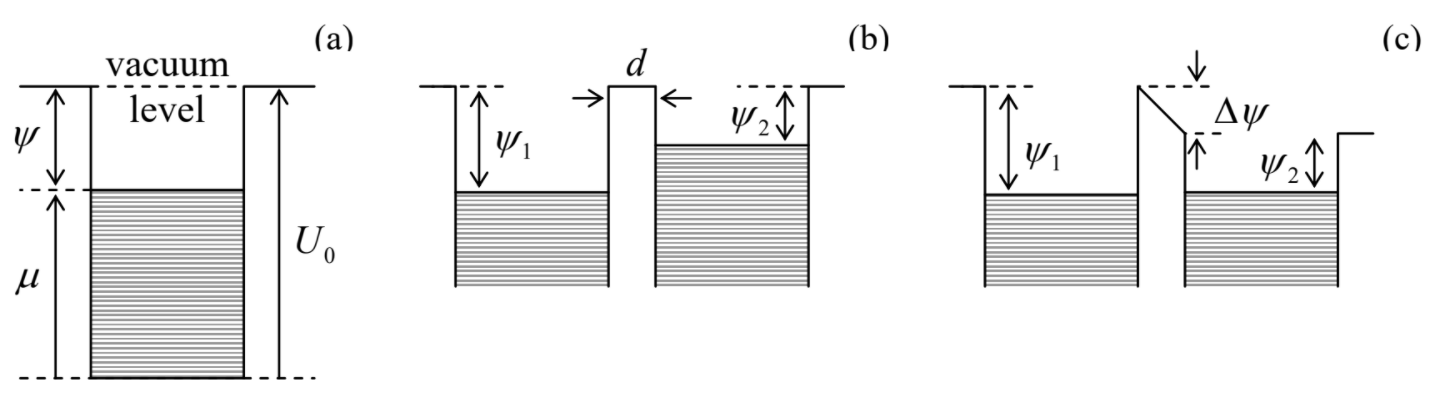
Ahora consideremos dos conductores, con diferentes valores de\(\Psi \), separados por una pequeña brecha espacial\(d\) — ver Figs. \(\PageIndex{1b,c}\). El panel (b) muestra el caso cuando el campo eléctrico\(\pmb{\mathscr{E}} = –\nabla \phi\) en el espacio libre entre los conductores es igual a cero, es decir, sus potenciales electrostáticos\(\phi\) son iguales. ²⁵ Si hay una oportunidad para que las partículas crucen el hueco (por ejemplo, ya sea mediante el salto activado térmicamente sobre la barrera potencial, discutida en Secs. 5.6-5.7, o la tunelización cuántica-mecánica a través de ella), habrá un flujo promedio de partículas desde el conductor con el nivel de Fermi más alto al que con el nivel de Fermi inferior, ²⁶ porque el equilibrio químico requiere su igualdad — ver Secs. 1.5 y 2.7. Si las partículas tienen una carga eléctrica (como lo hacen los electrones), el equilibrio se logrará automáticamente recargando el condensador efectivo formado por los conductores, hasta que la diferencia de energía electrostática\(q\Delta \phi\) alcance el valor reproduciendo el de las funciones de trabajo (Figura\(\PageIndex{1c}\)). Así que para la diferencia de potencial de equilibrio ²⁷ podemos escribir

\[ q\Delta \phi = \Delta \Psi = −\Delta \mu . \label{44}\]

En este equilibrio, el campo eléctrico en la brecha entre los conductores es

\[\pmb{\mathscr{E}} = -\frac{\Delta \phi}{d}\mathbf{n} = \frac{\Delta \mu}{qd} \mathbf{n} = \frac{\nabla \mu}{q} ; \label{45}\]

en la Figura\(\PageIndex{1c}\) este campo es claramente visible como la inclinación del perfil de potencial eléctrico. Comparando la Ecuación (\ ref {45}) con la definición (\ ref {42}) del campo eléctrico efectivo\(\mathcal{E}\), vemos que el equilibrio, es decir, la ausencia de corriente a través de la barrera potencial, se logra exactamente cuando\(\mathcal{E} = 0\), de acuerdo con la Ecuación (\ ref {41}).

La dicotomía del campo eléctrico\(\pmb{\mathscr{E}} \leftrightarrow \mathcal{E}\),, plantea una pregunta natural: ¿de cuál de estos campos estamos hablando en la práctica cotidiana y de laboratorio? Ante alguna contemplación, el lector debe estar de acuerdo en que la mayoría de nuestras mediciones de campo eléctrico se realizan indirectamente, midiendo los voltajes correspondientes —con voltímetros—. Una gran mayoría de estos instrumentos pertenecen a la llamada variedad electrodinámica, que se basa en la medición de una pequeña corriente que fluye a través del voltímetro. ²⁸ Como muestra la Ecuación (\ ref {41}), dichos voltímetros electrodinámicos miden la diferencia de potencial electroquímico\(\Delta \mu '/q\). Sin embargo, existe una rara raza de voltímetros electrostáticos (también llamados “electrómetros”) que miden la diferencia de potencial electrostático\(\Delta \phi\) entre dos conductores. Una forma de implementar dicho instrumento es usar un voltímetro electrodinámico ordinario, pero con el punto de referencia establecido en la condición de banda plana (Figura\(\PageIndex{1b}\)) entre los conductores. (Esta condición puede ser detectada por la fuga de carga eléctrica en las superficies adyacentes de los conductores, y por lo tanto por la ausencia de su modulación en el tiempo si la distancia entre las superficies se modula periódicamente).

Ahora permítanme volver a la Ecuación (\ ref {41}) y hacer dos observaciones muy importantes. Primero, dice que en presencia de un campo eléctrico, la corriente desaparece solo si\(\nabla \mu ' = 0\), es decir, que el potencial electroquímico\(\mu '\), más que el potencial químico\(\mu \), tiene que ser independiente de la posición en un sistema en equilibrio termodinámico (térmico, químico y eléctrico) de un sistema de conducción. Este resultado no contradice de ninguna manera las relaciones termodinámicas fundamentales para\(\mu\) discutidas en la Sec. 1.5, o las relaciones estadísticas que involucran\(\mu \), las cuales fueron discutidas en la Sec. 2.7 y posteriores. En efecto, según la Ecuación (\ ref {40}),\(\mu '(\mathbf{r})\) es “meramente” el potencial químico referido al valor local de la energía electrostática\(q\phi (\mathbf{r})\), y en todas las partes anteriores del curso, se suponía que esta energía era constante a través del sistema.

Segundo, anotar otra interpretación de la Ecuación (\ ref {41}), que se puede lograr modificando la Ecuación (\ ref {38}) para el caso particular del gas clásico. De hecho, la densidad local\(n \equiv N/V\) del gas obedece a la Ecuación (\(3.2.1-3.2.2\)), que puede ser reescrita como

\[n(\mathbf{r}) = \text{const}\times\exp \left\{\frac{\mu (\mathbf{r})}{T}\right\}. \label{46}\]

Tomando el gradiente espacial de ambos lados de esta relación (todavía en constante\(T\)), obtenemos

\[\nabla n = \text{const}\times \frac{1}{T} \exp \left\{\frac{\mu}{T}\right\} \nabla \mu = \frac{n}{T} \nabla \mu , \label{47}\]

para que\(\nabla \mu = (T/n)\nabla n\), y la Ecuación (\ ref {41}), con\(\sigma\) dada por la Ecuación (\(6.2.14\)), se pueda refundir como

\[\mathbf{j} = \sigma \left(-\frac{\nabla \mu '}{q}\right) \equiv \frac{q^2 \tau}{m} n \left( - \nabla \phi - \frac{1}{q} \nabla \mu \right) \equiv q \frac{\tau}{m} ( nq \pmb{\mathscr{E}} - T \nabla n ). \label{48}\]

De ahí que la densidad de corriente pueda verse como constituida por dos partes independientes: una por deriva de partículas inducida por el campo eléctrico “habitual”\(\pmb{\mathscr{E}} = –\nabla \phi \), y otra por su difusión — ver Ecuación (\(5.6.14\)) y su discusión. Esta es exactamente la física del término “misterioso”\(\nabla \mu\) en Ecuación (\ ref {42}), aunque su forma simple (\ ref {48}) es válida solo en el límite clásico.

\[\frac{\partial (qn)}{\partial t} + \nabla \cdot \mathbf{j} = 0, \label{49}\]

obtenemos (después de la división de todos los términos por\(q\tau /m\)) la llamada ecuación de derivación-difusión: ³⁰

Ecuación de difusión-deriva:

\[\boxed{ \frac{m}{\tau} \frac{\partial n}{\partial t} = \nabla (n \nabla U ) + T \nabla^2 n, \quad \text{ with } U \equiv q \phi . } \label{50}\]

Comparándolo con la ecuación (\(5.6.18\)), vemos que la ecuación de derivación-difusión es idéntica a la ecuación de Smoluchowski, ³¹ siempre que paralelemos la relación\(\tau /m\) con la movilidad\(\mu_m = 1/\eta\) de la partícula browniana. Ahora usando la relación Einstein (\(5.5.17\)), vemos que la constante\(D\) de difusión efectiva del gas clásico de partículas similares es

\[D = \frac{\tau T}{m}. \label{51a}\]

Esta importante relación se representa con mayor frecuencia en cualquiera de otras dos formas. Primero, dado que los raros eventos de dispersión que estamos considerando no cambian las estadísticas del gas en equilibrio térmico, aún podemos usar el resultado MaxWell distribution (\(3.1.9\)) para la velocidad media-cuadrada\(\langle v^2\rangle \), para refundir la Ecuación (\ ref {51a}) como

\[D=\frac{1}{3} \langle v^2 \rangle \tau . \label{51b}\]

Una forma más popular de la misma relación utiliza la noción del camino libre medio\(l\), que puede definirse como la distancia promedio que pasa la partícula entre dos eventos de dispersión secuenciales:

\[D=\frac{1}{3} l \langle v^2 \rangle^{1/2} , \quad \text{ with } l \equiv \langle v^2 \rangle^{1/2} \tau . \label{51c}\]

En las formas (\ ref {51b}) - (\ ref {51c}), el resultado para tiene más\(D\) sentido físico, porque puede derivarse fácilmente (es cierto, con cierta incertidumbre del coeficiente numérico) a partir de simples argumentos cinemáticos —la tarea dejada para el ejercicio del lector. Obsérvese que dado que la definición de\(\tau\) en la Ecuación (\(6.1.17\)) es fenomenológica, también lo es la definición anterior de\(l\); es por ello que son posibles varias definiciones de este parámetro, que pueden diferir por un factor numérico del orden de 1.

Tenga en cuenta también que usando la ecuación (\ ref {51a}), la ecuación (\ ref {48}) puede reescribirse como una expresión para la densidad de flujo de partículas\(\mathbf{j}_n \equiv n \mathbf{j}_w = \mathbf{j} / q\):

\[ \mathbf{j}_n = n \mu_m q \pmb{\mathscr{E}} - D \nabla n, \label{52}\]

con el primer término en el lado derecho describiendo la deriva de las partículas, mientras que el segundo, su difusión. Discutiré la aplicación de esta ecuación al caso más importante de gases no degenerados (“cuasi clásicos”) de electrones y agujeros en semiconductores, en la siguiente sección.

Para completar esta sección, permítanme enfatizar nuevamente que la ecuación matemáticamente similar a la deriva de difusión (\ ref {50}) y la ecuación de Smoluchowski (\(5.6.18\)) describen diferentes situaciones físicas. De hecho, nuestro (o más bien el de Einstein y Smoluchowski: -) tratamiento del movimiento browniano en el Capítulo 5 se basó en una fuerte jerarquía del sistema, consistente en una gran “partícula browniana” en un ambiente de muchas partículas más pequeñas —“ moléculas”. Por otro lado, en este capítulo estamos considerando un gas de partículas similares. Sin embargo, las ecuaciones que describen la dinámica de su distribución de probabilidad, son las mismas, al menos en el marco de la ecuación de transporte de Boltzmann con la aproximación relajación-tiempo (\(6.1.17\)) de la integral de dispersión. El origen de esta similitud es el hecho de que la Ecuación (\(6.1.12\)) también es claramente aplicable a una partícula browniana, siendo cada evento de “dispersión” el impacto de la partícula por una molécula aleatoria de su entorno. Dado que, debido a la jerarquía de masas, el cambio de momento de la partícula en cada evento es muy pequeño, la integral de dispersión tiene que ser local, es decir, depender solo de w al\(\mathbf{p}\) mismo impulso que el lado izquierdo de la ecuación de Boltzmann, de manera que la aproximación del tiempo de relajación (\(6.1.17\)) es absolutamente natural —de hecho, más natural que para nuestro caso actual de partículas similares.