1.1: Ondas transversales y longitudinales
- Page ID
- 126118
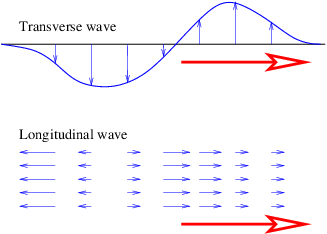
A excepción de la luz, las ondas son ondulaciones en un medio material. Por ejemplo, las olas oceánicas son ondulaciones (casi) verticales en la posición de las parcelas de agua. Las oscilaciones en parcelas vecinas son escalonadas de tal manera que un patrón se mueve a través de la superficie del océano. Las ondas en un slinky son transversales, en que el movimiento del material del slinky es perpendicular a la orientación del slinky, o son longitudinales, con movimiento material en la dirección del slinky estirado. (Véase la figura 1.1.) Algunos medios soportan solo ondas longitudinales, otros soportan solo ondas transversales, mientras que otros soportan ambos tipos. Las ondas de luz son puramente transversales, mientras que las ondas sonoras son puramente longitudinales. Las olas oceánicas son una peculiar mezcla de transversal y longitudinal, con parcelas de agua moviéndose en trayectorias elípticas a medida que pasan las olas.
La luz es una forma de radiación electromagnética. Las ondulaciones en una onda electromagnética ocurren en los campos eléctrico y magnético. Estas oscilaciones son perpendiculares a la dirección de movimiento de la onda (en un vacío), por lo que llamamos a la luz una onda transversal.
Olas

Un tipo de onda particularmente simple, la onda sinusoidal, se ilustra en la figura 1.2. Esto tiene la forma matemática
\[h (x) = h0sin(2πx ∕λ), \label{1.1}\]
donde\(h \) está el desplazamiento (que puede ser longitudinal o transversal),\(h\) 0 es el desplazamiento máximo, también llamado la amplitud de la onda, y\(λ \) es la longitud de onda. Se supone que el comportamiento oscilatorio de la onda continúa hasta el infinito tanto en la\(x \) dirección positiva como en la negativa. Observe que la longitud de onda es la distancia a través de la cual la función sinusoidal completa un ciclo completo. La cresta y el valle de una ola son las ubicaciones de los desplazamientos máximo y mínimo, como se ve en la figura 1.2.
Hasta el momento sólo hemos considerado una onda sinusoidal tal como aparece en un momento determinado. Todas las olas interesantes se mueven con el tiempo. El movimiento de una onda sinusoidal hacia la derecha una distancia\(d \) puede contabilizarse reemplazando\(x \) en la fórmula anterior por\(x \) -\(d\). Si este movimiento ocurre en el tiempo\(t\), entonces la onda se mueve a velocidad\(c \) =\(d∕t\). Resolver esto\(d \) y sustituirlo produce una fórmula para el desplazamiento de una onda sinusoidal en función tanto de la distancia\(x \) como del tiempo\(t\):
\[h(x,t) = h0sin[2π(x - ct)∕λ]. \label{1.2}\]
El tiempo para que una onda se mueva una longitud de onda se denomina período de la onda:\(T \) =\(λ∕c\). Así, también podemos escribir
\[h(x,t) = h sin[2π(x∕ λ - t∕T )]. 0 \label{1.3}\]
A los físicos realmente les gusta escribir la ecuación para una onda sinusoidal en una forma ligeramente más simple. Definiendo el número de onda como\(k \) = 2\(π∕λ \) y la frecuencia angular como\(ω \) = 2\(π∕T\), escribimos
\[h(x,t) = h0 sin(kx - ωt ). \label{1.4}\]
Normalmente pensamos en la frecuencia del movimiento oscilatorio como el número de ciclos completados por segundo. A esto se le llama la frecuencia rotacional, y viene dada por\(f \) = 1\(∕T\). Se relaciona con la frecuencia angular por\(ω \) = 2\(πf\). La frecuencia rotacional suele ser más fácil de medir que la frecuencia angular, pero la frecuencia angular tiende a ser utilizada con mayor frecuencia en discusiones teóricas. Como se mostró anteriormente, convertir entre los dos no es difícil. La frecuencia rotacional se mide en unidades de hercios, abreviado Hz; 1 Hz = 1 ciclo s - 1. La frecuencia angular también tiene las dimensiones de tiempo inverso, por ejemplo, radián s - 1, pero el término “hertz” generalmente se reserva solo para frecuencia rotacional.
El argumento de la función seno es por definición un ángulo. Nos referimos a este ángulo como la fase de la onda,\(ϕ \) =\(kx \) -\(ωt\). La diferencia en la fase de una onda en tiempo fijo sobre una distancia de una longitud de onda es 2\(π\), así como la diferencia de fase en posición fija durante un intervalo de tiempo de un período de onda.
Dado que los ángulos son adimensionales, normalmente no incluimos esto en las unidades para frecuencia. Sin embargo, a veces aclara las cosas para referirse a las dimensiones de la frecuencia rotacional como “rotaciones por segundo” o frecuencia angular como “radianes por segundo”.
Como se señaló anteriormente, llamamos\(h\) 0, el desplazamiento máximo de la onda, la amplitud. Muchas veces nos interesa la intensidad de una onda, que es proporcional al cuadrado de la amplitud. La intensidad suele estar relacionada con la cantidad de energía que transporta una ola.
La velocidad de ola que hemos definido anteriormente,\(c \) =\(λ∕T\), en realidad se llama la velocidad de fase. Dado que\(λ \) = 2\(π∕k \) y\(T \) = 2\(π∕ω\), podemos escribir la velocidad de fase en términos de la frecuencia angular y el número de onda:
\[c = ω- (phase speed ). k \label{1.5}\]
Tipos de Olas
Para hacer más concreto el material anterior, examinamos ahora las características de varios tipos de olas que se pueden observar en el mundo real.
Olas de superficie oceánica
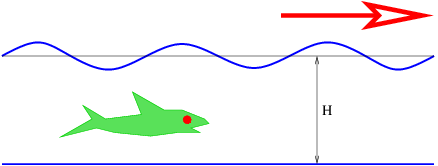
Estas olas se manifiestan como ondulaciones de la superficie oceánica como se ve en la figura 1.3. La velocidad de las olas oceánicas viene dada por la fórmula
\[ ( )1∕2 gtanh-(kH-)- c = k , \label{1.6} \]
donde\(g \) = 9\(.\) 8 m s - 2 es la fuerza gravitacional de la tierra por unidad de masa,\(H \) es la profundidad del océano, y la tangente hiperbólica se define como 1
\[ exp (x) - exp(- x) tanh(x) = ------------------. exp (x) + exp(- x) \label{1.7} \]
La ecuación para la velocidad de las olas oceánicas proviene de la teoría de las oscilaciones de una superficie fluida en un campo gravicional.
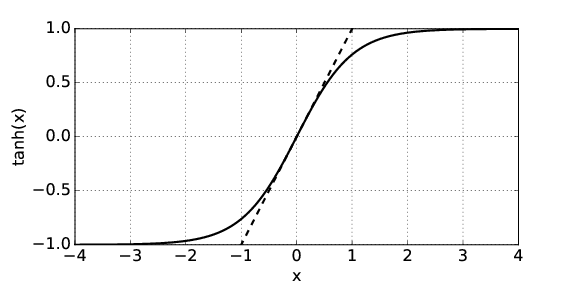
Como muestra la figura 1.4, para |\(x\) |1, podemos aproximar la tangente hiperbólica por tanh (\(x\)) ≈\(x\), mientras que para |\(x\) |≫ 1 es +1 para\(x > \) 0 y - 1 para\(x < \) 0. Esto lleva a dos límites: Since\(x \) =\(kH\), el límite de aguas poco profundas, que ocurre\(kH \) cuando 1, produce una velocidad de ola de
\[c ≈ (gH )1∕2, (shallow water waves), \label{1.8}\]
mientras que el límite de aguas profundas, que ocurre cuando\(kH \) ≫ 1, rinde
\[c ≈ (g∕k )1∕2, (deep water waves ). \label{1.9}\]
Observe que la velocidad de las olas de aguas poco profundas depende únicamente de la profundidad del agua y de\(g\). En otras palabras, todas las olas de aguas poco profundas se mueven a la misma velocidad. Por otro lado, las ondas de aguas profundas de mayor longitud de onda (y por lo tanto de menor número de onda) se mueven más rápidamente que aquellas con longitud de onda más corta. Las ondas para las cuales la velocidad de onda varía con la longitud de onda se denominan dispersivas. Así, las olas de aguas profundas son dispersivas, mientras que las de aguas poco profundas son no dispersivas.
Para las olas de agua con longitudes de onda de unos pocos centímetros o menos, la tensión superficial se vuelve importante para la dinámica de las olas. En el caso de aguas profundas, la velocidad de onda a longitudes de onda cortas viene dada por la fórmula
\[c = (g∕k + Ak )1∕2 \label{1.10}\]
donde la constante\(A \) está relacionada con un efecto llamado tensión superficial. Para una interfaz aire-agua cerca de la temperatura ambiente,\(A \) ≈ 74 cm 3 s - 2.
Ondas sonoras
El sonido es una onda longitudinal de compresión-expansión en un fluido. La velocidad de onda para el sonido en un gas ideal es
\[ 1∕2 c = (γRTabs ) \label{1.11}\]
donde\(γ \) y\(R \) son constantes y\(T\) abs es la temperatura absoluta. La temperatura absoluta se mide en Kelvins y se da numéricamente por
\[Tabs = TC + 273∘ \label{1.12}\]
donde\(T\) C es la temperatura en grados Celsius. La frecuencia angular de las ondas sonoras viene dada por
\[ω = ck = (γRTabs )1∕2k. \label{1.13}\]
La velocidad del sonido en el aire a temperaturas normales es de aproximadamente 340 m s - 1.
Luz
La luz se mueve en un vacío a una velocidad de\(c\) vac = 3 × 10 8 m s - 1. En materiales transparentes se mueve a una velocidad menor que\(c\) vac por un factor\(n \) que se denomina índice de refracción del material:
\[c = c ∕n. vac \label{1.14}\]
A menudo, el índice de refracción toma la forma
\[n2 ≈ 1 + ----A------, 1 - (k ∕kR)2 \label{1.15}\]
donde\(k \) es el número de onda y\(k\) R y\(A \) son constantes positivas características del material. La frecuencia angular de la luz en un medio transparente es así
\[ω = kc = kcvac∕n. \label{1.16}\]
Principio de superposición
Se encuentra empíricamente que mientras las amplitudes de las ondas en la mayoría de los medios sean pequeñas, dos ondas en la misma ubicación física no interactúan entre sí. Así, por ejemplo, dos ondas que se mueven en sentido contrario simplemente pasan una a través de la otra sin que se cambien sus formas o amplitudes. Cuando se coloca, el desplazamiento total de las olas es solo la suma de los desplazamientos de las olas individuales. A esto se le llama el principio de superposición. A una amplitud suficientemente grande, el principio de superposición a menudo se descompone: las ondas que interactúan pueden dispersarse unas de otras, perder amplitud o cambiar su forma.
La interferencia es una consecuencia del principio de superposición. Cuando se superponen dos o más ondas, el desplazamiento de onda neta es solo la suma algebraica de los desplazamientos de las ondas individuales. Dado que estos desplazamientos pueden ser positivos o negativos, el desplazamiento neto puede ser mayor o menor que los desplazamientos individuales de las olas. El primer caso, que ocurre cuando ambos desplazamientos son del mismo signo, se denomina interferencia constructiva, mientras que la interferencia destructiva ocurre cuando son de signo opuesto.
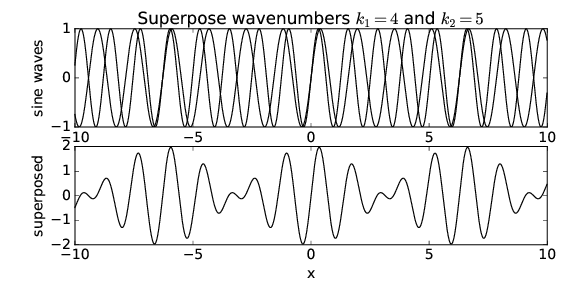
Veamos qué sucede cuando superponemos dos ondas sinusoidales con diferentes números de onda. La Figura 1.5 muestra la superposición de dos ondas con números de onda\(k\) 1 = 4 y\(k\) 2 = 5. Observe que el resultado es una onda con aproximadamente la misma longitud de onda que las dos ondas iniciales, pero que varía en amplitud dependiendo de si las dos ondas sinusoidales están interfiriendo constructiva o destructivamente. Nosotros decimos que las ondas están en fase si están interfiriendo constructivamente, y están fuera de fase si están interfiriendo destructivamente.
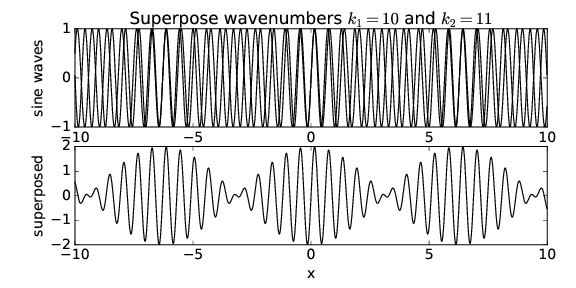
¿Qué sucede cuando se cambian los números de onda de las dos ondas sinusoidales? La Figura 1.6 muestra el resultado cuando\(k\) 1 = 10 y\(k\) 2 = 11. Observe que aunque la longitud de onda de la onda resultante disminuye, las ubicaciones donde la amplitud es máxima tienen la misma separación que en la figura 1.5.\(x \)
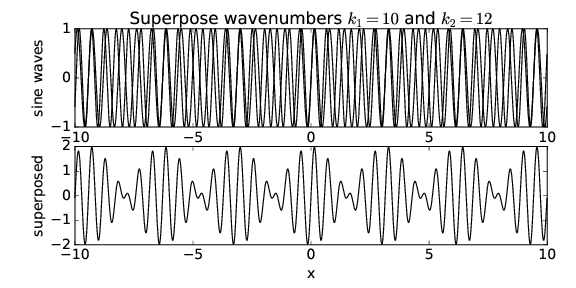
Si superponemos ondas con\(k\) 1 = 10 y\(k\) 2 = 12, como se muestra en la figura 1.7, vemos que el\(x \) espaciamiento de las regiones de máxima amplitud ha disminuido en un factor de dos. Así, mientras que el número de onda de la onda resultante parece estar relacionado con algo así como el promedio de los números de onda de las ondas componentes, el espaciamiento entre regiones de amplitud de onda máxima parece ir inversamente con la diferencia de los números de onda de las ondas componentes. En otras palabras, si\(k\) 1 y\(k\) 2 están muy juntos, los máximos de amplitud están muy separados y viceversa.

Podemos representar simbólicamente las ondas sinusoidales que componen las figuras 1.5, 1.6 y 1.7 mediante una gráfica como la que se muestra en la figura 1.8. Las amplitudes y números de onda de cada una de las ondas sinusoidales se indican mediante líneas verticales en esta figura.
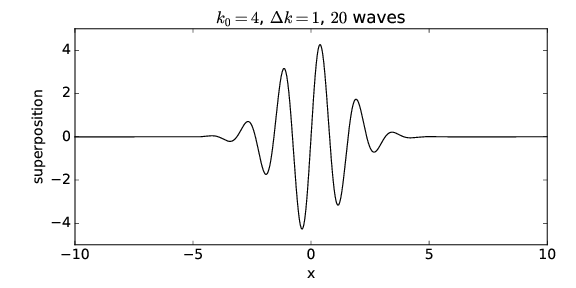

Las regiones de gran amplitud de onda se denominan paquetes de onda. Los paquetes de ondas jugarán un papel central en lo que va a seguir, por lo que es importante que adquieran una buena comprensión de ellos. Los paquetes de onda producidos por solo dos ondas sinusoidales no están bien separados a lo largo del\(x\) eje. Sin embargo, si superponemos muchas ondas, podemos producir un paquete de ondas aisladas. Por ejemplo, la figura 1.9 muestra los resultados de superponer 20 ondas sinusoidales con números de onda\(k \) = 0\(.\) 4\(m\),\(m \) = 1\(, \) 2\(,\)\(…\)\(, \) 20, donde las amplitudes de las ondas son mayores para los números de onda cercanos a\(k \) = 4. En particular, suponemos que la amplitud de cada onda sinusoidal es proporcional a exp [- (\(k \)-\(k\) 0) 2\(∕\) Δ\(k\) 2], donde\(k\) 0 = 4 define el máximo de la distribución de números de onda y Δ\(k \) = 1 define el ancho medio de esta distribución. Las amplitudes de cada una de las ondas sinusoidales que componen el paquete de ondas en la figura 1.9 se muestran esquemáticamente en la figura 1.10.
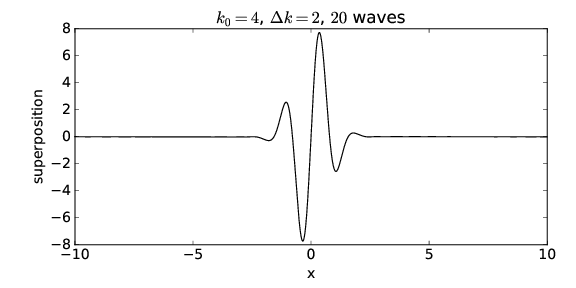

La cantidad Δ\(k \) controla la distribución de las ondas sinusoidales que se superponen, solo aquellas ondas con un número de onda\(k \) dentro\(k\) de aproximadamente Δ del número de onda central\(k\) 0 del paquete de ondas, es decir, para 3 ≤ \(k \)≤ 5 en este caso, contribuir significativamente a la suma. Si Δ\(k \) se cambia a 2, de manera que los números de onda en el rango 2 \(k \)≤ ≤ 6 contribuyen significativamente, el paquete de ondas se vuelve más estrecho, como se muestra en las figuras 1.11 y 1.12. Δ\(k \) se llama propagación del número de onda del paquete de onda, y evidentemente juega un papel similar a la diferencia en los números de onda en la superposición de dos ondas sinusoidales: cuanto mayor es la dispersión del número de onda, menor es el tamaño físico del paquete de ondas. Además, el número de onda de las oscilaciones dentro del paquete de ondas viene dado aproximadamente por el número de onda central.
Podemos entender mejor cómo funcionan los paquetes de ondas analizando matemáticamente el caso simple de superposición de dos ondas sinusoidales. Definamos\(k\) 0 = (\(k\)1 +\(k\) 2)\(∕\) 2 donde\(k\) 1 y\(k\) 2 son los números de onda de las ondas componentes. Además, pongamos Δ\(k \) = (\(k\)2 -\(k\) 1)\(∕\) 2. Las cantidades\(k\) 0 y Δ\(k \) se ilustran gráficamente en la figura 1.8. Podemos escribir\(k\) 1 =\(k\) 0 - Δ\(k \) y\(k\) 2 =\(k\) 0 + Δ\(k\) y usar la identidad trigonométrica sin (\(a \)+\(b\) ) = sin (\(a\)) cos (\(b\)) + cos (\(a\)) sin (\(b\)) para encontrar
\[sin (k1x) + sin(k2x) = sin [(k0 - Δk )x] + sin[(k0 + Δk )x] = sin (k0x)cos(Δkx ) - cos(k0x)sin(Δkx ) + sin (k0x)cos(Δkx ) + cos(k0x)sin(Δkx ) = 2sin(k0x) cos(Δkx ). \label{1.17} \]
El factor seno en la línea inferior de la ecuación anterior produce las oscilaciones dentro del paquete de ondas, y como se especuló anteriormente, esta oscilación tiene un número de onda\(k\) 0 igual al promedio de los números de onda de las ondas componentes. El factor coseno modula esta onda con un espaciamiento entre regiones de amplitud máxima de
\[Δx = π∕Δk. \label{1.18}\]
Así, como observamos en los ejemplos anteriores, la longitud del paquete de onda Δ\(x \) está inversamente relacionada con la propagación de los números de onda Δ\(k \) (que en este caso es solo la diferencia entre los dos números de onda) de las ondas componentes. Esta relación es fundamental para el principio de incertidumbre de la mecánica cuántica.
Beats
Supongamos que dos ondas sonoras de diferente frecuencia pero igual amplitud inciden en su oído al mismo tiempo. El desplazamiento percibido por tu oído es la superposición de estas dos ondas, con dependencia del tiempo
\[h(t) = sin(ω t) + sin (ω t) = 2 sin (ω t)cos(Δ ωt), 1 2 0 \label{1.19}\]
donde hemos usado el truco matemático anterior, y donde\(ω\) 0 = (\(ω\)1 +\(ω\) 2)\(∕\) 2 y Δ\(ω \) = (\(ω\)2 -\(ω\) 1)\(∕\) 2. Lo que realmente escuchas es un tono con frecuencia angular\(ω\) 0 que se desvanece dentro y fuera con el punto
\[T = π∕|Δω | = 2π∕|ω - ω | = 1∕|f - f |. beat 2 1 2 1 \label{1.20}\]
La frecuencia de latido es simplemente
\[fbeat = 1 ∕Tbeat = |f2 - f1|. \label{1.21}\]
Observe cómo los latidos son el análogo de tiempo de los paquetes de onda: las matemáticas son las mismas excepto que la frecuencia reemplaza al número de onda y el tiempo reemplaza al espacio.
Interferómetros
Un interferómetro es un dispositivo que divide un haz de luz (u otra onda) en dos sub-haces, desplaza la fase de un subhaz con respecto al otro, y luego superpone los sub-haces para que interfieran constructiva o destructivamente, dependiendo de la magnitud del desplazamiento de fase entre ellos. En esta sección estudiamos el interferómetro Michelson y los efectos interferométricos en películas delgadas.
Interferómetro Michelson
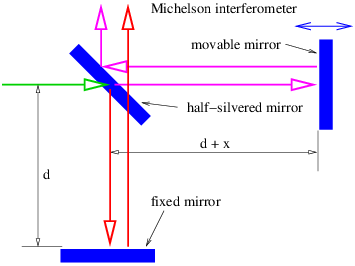
El físico estadounidense Albert Michelson inventó el interferómetro óptico ilustrado en la figura 1.13. El haz entrante se divide en dos haces por el espejo medio plateado. Cada sub-haz se refleja en otro espejo que lo devuelve al espejo semiplateado, donde los dos sub-haces se recombinan como se muestra. Uno de los espejos reflectantes es movible por un dispositivo micrométrico sensible, permitiendo que se altere la longitud de trayectoria del sub-haz correspondiente, y por lo tanto la relación de fase entre los dos sub-haces. Como muestra la figura 1.13, la diferencia en la longitud de la trayectoria entre los dos sub-haces es de 2\(x \) porque la subviga horizontal atraviesa la trayectoria dos veces. Así, la interferencia constructiva ocurre cuando esta diferencia de trayectoria es un número integral de longitudes de onda, es decir,
\[2x = m λ, m = 0, ±1, ±2,... (Michelson interferometer ) \label{1.22}\]
donde\(λ \) es la longitud de onda de la onda y\(m \) es un entero. Tenga en cuenta que\(m \) es el número de longitudes de onda que se ajusta uniformemente en la distancia 2\(x\).
Películas
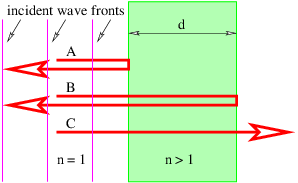
Uno de los ejemplos más reveladores de interferencia ocurre cuando la luz interactúa con una película delgada de material transparente como una burbuja de jabón. La Figura 1.14 muestra cómo una onda plana que normalmente incide sobre la película es reflejada parcialmente por las superficies delantera y trasera. Las ondas reflejadas en las superficies delantera y trasera de la película interfieren entre sí. La interferencia puede ser constructiva o destructiva dependiendo de la diferencia de fase entre las dos ondas reflejadas.
Si la longitud de onda de la onda entrante es\(λ\), uno esperaría ingenuamente que ocurriera interferencia constructiva entre los haces A y B si 2\(d \) fueran un múltiplo integral de\(λ\).
Dos factores complican esta imagen. Primero, la longitud de onda dentro de la película no es\(λ\)\(λ∕n\), sino, donde\(n \) está el índice de refracción de la película. Entonces se produciría interferencia constructiva si 2\(d \) =\(mλ∕n\). En segundo lugar, resulta que se produce un desplazamiento de fase adicional de media longitud de onda al reflexionar cuando la onda incide sobre material con un índice de refracción mayor que el medio en el que se sumerge el haz incidente. Este desplazamiento de fase no ocurre cuando la luz se refleja desde una región con un índice de refracción más bajo que el sentido por el haz incidente. Por lo tanto, el haz B no adquiere ningún desplazamiento de fase adicional tras la reflexión. Como consecuencia, la interferencia constructiva ocurre realmente cuando
\[2d = (m + 1∕2)λ ∕n, m = 0,1,2,... (constructive interference) \label{1.23}\]
mientras que la interferencia destructiva resulta cuando
\[2d = m λ∕n, m = 0,1,2,... (destructive interference). \label{1.24}\]
Cuando miramos una burbuja de jabón, vemos bandas de colores reflejadas desde una fuente de luz. ¿Cuál es el origen de estas bandas? La luz de fuentes ordinarias es generalmente una mezcla de longitudes de onda que van desde aproximadamente\(λ \) = 4\(.\) 5 × 10 - 7 m (luz violeta) hasta\(λ \) = 6\(.\) 5 × 10 - 7 m (luz roja). Entre violeta y rojo también tenemos luz azul, verde y amarilla, en ese orden. Debido a las diferentes longitudes de onda asociadas a diferentes colores, es claro que para una fuente de luz mixta tendremos algunos colores interfiriendo constructivamente mientras que otros interfieren destructivamente. Aquellos que sufren una interferencia constructiva serán visibles en la reflexión, mientras que los que sufren interferencia destructiva no lo harán.
Otro factor entra también. Si la luz normalmente no incide sobre la película, la diferencia en las distancias recorridas entre los haces reflejados en las caras frontal y posterior de la película no será solo el doble del grosor de la película. Para entender este caso cuantitativamente, necesitamos el concepto de refracción, que se desarrollará posteriormente en el contexto de la óptica geométrica. Sin embargo, debe quedar claro que diferentes longitudes de onda sufrirán interferencia constructiva para diferentes ángulos de incidencia de la luz entrante. Diferentes porciones de la película delgada se verán en general en diferentes ángulos, y por lo tanto exhibirán diferentes colores bajo reflexión, dando como resultado los patrones coloridos que normalmente se ven en las burbujas de jabón.
Revisión — Derivados
Esta sección proporciona una revisión rápida de la idea del derivado. A menudo nos interesa la pendiente de una línea tangente a una función\(y\) (\(x\)) a algún valor de\(x\). Esta pendiente se llama la derivada y se denota\(dy∕dx\). Dado que una línea tangente a la función se puede definir en cualquier punto\(x\), la derivada en sí misma es una función de\(x\):
\[ dy(x) g(x ) = -----. dx \label{1.25} \]
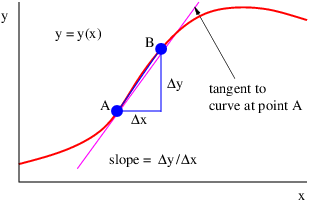
Como ilustra la figura 1.15, la pendiente de la línea tangente en algún punto de la función puede aproximarse por la pendiente de una línea que conecta dos puntos, A y B, establecer una distancia finita en la curva:
\[dy-≈ Δy-. dx Δx \label{1.26}\]
A medida que B se acerca a A, la aproximación se vuelve mejor. En el límite cuando B se acerca infinitamente a A, es exacto.
Ahora se dan las derivadas de algunas funciones comunes. En cada caso\(a \) es una constante.
\[ a dx--= axa-1 dx \]
(1.27)\[d--exp(ax) = a exp(ax ) dx \label{1.28}\]
\[d 1 ---log (ax) = -- dx x \label{1.29} \]
\[ d ---sin(ax) = a cos(ax) dx \]
(1.30)\[ d dx-cos(ax ) = - a sin (ax) \label{1.31}\]
\[daf(x ) df(x) -------= a------ dx dx \label{1.32} \]
\[ d df (x ) dg(x) ---[f (x ) + g (x )] =-----+ ------ dx dx dx \label{1.33} \]
\[d df(x) dg(x) --f (x)g(x) = -----g (x ) + f (x)----- (product rule) dx dx dx \label{1.34} \]
\[d df dy --f (y ) = ----- (chain rule) dx dydx \label{1.35} \]
Las reglas de producto y cadena se utilizan para calcular las derivadas de funciones complejas. Por ejemplo,
\[ d d sin(x ) dcos(x) ---(sin (x )cos(x)) = --------cos(x) + sin (x )--------= cos2(x ) - sin2(x) dx dx dx \]
y
\[-d-log(sin(x )) = --1---dsin(x)-= cos(x-). dx sin(x) dx sin(x ) \]
Velocidad de Grupo
Ahora hacemos la siguiente pregunta: ¿Qué tan rápido se mueven los paquetes de onda? Sorprendentemente, a menudo encontramos que los paquetes de ondas se mueven a una velocidad muy diferente a la velocidad de fase\(ω∕k\),\(c \) =, de la onda que compone el paquete de ondas.
Encontraremos que la velocidad de movimiento de los paquetes de ondas, referida como la velocidad del grupo, viene dada por
\[ | dω-|| u = dk || (group velocity). k=k0 \label{1.36} \]
La derivada de\(ω\) (\(k\)) con respecto a\(k \) se calcula primero y luego se evalúa en\(k \) =\(k\) 0, el número de onda central del paquete de onda de interés.
La relación entre la frecuencia angular y el número de onda para una onda,\(ω \) =\(ω\) (\(k\)), depende del tipo de onda que se esté considerando. Sea cual sea esta relación que resulte ser en un caso particular, se le llama relación de dispersión para el tipo de onda en cuestión.
Como ejemplo de un cálculo de velocidad grupal, supongamos que queremos encontrar la velocidad de paquetes de olas oceánicas profundas para una longitud de onda central de\(λ\) 0 = 60 m. Esto corresponde a un número de onda central de\(k\) 0 = 2\(π∕λ\) 0 ≈ 0\(.\) 1 m - 1. La velocidad de fase de las olas del océano profundo es\(c \) = (\(g∕k\)) 1 2. Sin embargo, desde\(c \) ≡\(ω∕k\), encontramos que la frecuencia de las olas del océano profundo es\(ω \) = (\(gk\)) 1 2. Por lo tanto, la velocidad del grupo es\(u \) ≡\(dω∕dk \) = (\(g∕k\)) 1\(∕\) 2 2 =\(c∕\) 2. Para el número de onda central especificado, encontramos que\(u \) ≈ (9\(.\) 8 m s - 2\(∕\) 0\(.\) 1 m - 1) 1 2\(∕\) 2 ≈ 5 m s - 1. Por el contrario, la velocidad de fase de las olas del océano profundo con esta longitud de onda es\(c \) ≈ 10 m s - 1.
Las ondas dispersivas son ondas en las que la velocidad de fase varía con el número de onda. Es fácil demostrar que las ondas dispersivas tienen velocidades de fase y grupo desiguales, mientras que estas velocidades son iguales para las ondas no dispersivas.
Derivación de la Fórmula de Velocidad de Grupo
Ahora derivamos la ecuación 1.36}. Es más fácil hacer esto para los paquetes de onda más simples, es decir, aquellos construidos a partir de la superposición de solo dos ondas sinusoidales. Procederemos sumando dos ondas con total dependencia de espacio y tiempo:
\[h = sin(k x - ω t) + sin(k x - ω t) 1 1 2 2 \label{1.37}\]
Después de manipulaciones algebraicas y trigonométricas familiares de secciones anteriores, encontramos
\[h = 2sin(k0x - ω0t)cos(Δkx - Δ ωt ), \label{1.38}\]
donde como antes tenemos\(k\) 0 = (\(k\)1 +\(k\) 2)\(∕\) 2,\(ω\) 0 = (\(ω\)1 +\(ω\) 2) \(∕\)2, Δ\(k \) = (\(k\)2 -\(k\) 1)\(∕\) 2 y Δ\(ω \) = (\(ω\)2 -\(ω\) 1)\(∕\) 2.
Nuevamente piensa en esto como una onda sinusoidal de frecuencia\(ω\) 0 y número de onda\(k\) 0 modulada por una función coseno. En este caso el patrón de modulación se mueve con una velocidad para mantener constante el argumento de la función coseno:
\[Δkx - Δ ωt = const. \label{1.39}\]
Diferenciar esto con respecto a\(t \) mientras se mantienen los rendimientos\(ω \) constantes Δ\(k \) y Δ
\[ dx- Δ-ω- u ≡ dt = Δk . \label{1.40}\]
En el límite en el que los deltas se vuelven muy pequeños, esto se reduce a la derivada
\[ dω u = --, dk \label{1.41} \]
que es el resultado deseado.
Ejemplos
Ahora ilustramos algunos ejemplos de velocidad de fase y velocidad de grupo mostrando el desplazamiento resultante de la superposición de dos ondas sinusoidales, según lo dado por la ecuación 1.38}, en el\(t \) plano\(x\) -. Este es un ejemplo de un diagrama espacio-tiempo, del cual veremos muchos ejemplos más adelante.
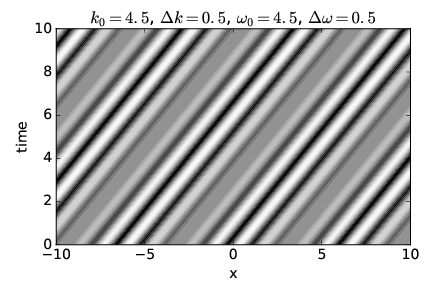
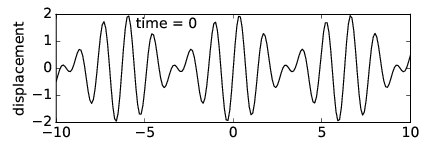
El panel superior de la figura 1.16 muestra un caso no dispersivo en el que la velocidad de fase es igual a la velocidad del grupo. Las regiones blanca y negra indican respectivamente fuertes crestas y valles de onda (es decir, regiones de grandes desplazamientos positivos y negativos), con grises que indican un desplazamiento cercano a cero. Las regiones con grandes desplazamientos indican la ubicación de los paquetes de ondas. Por lo tanto, las posiciones de las ondas y los paquetes de ondas en cualquier momento dado pueden determinarse dibujando una línea horizontal a través de la gráfica en el momento deseado y examinando las variaciones en el desplazamiento de onda a lo largo de esta línea. El panel inferior de esta figura muestra el desplazamiento de onda\(x \) en función del tiempo\(t \) = 0 como una ayuda para la interpretación del panel superior.
Observe que a medida que aumenta el tiempo, las crestas se mueven hacia la derecha. Esto corresponde al movimiento de las ondas dentro de los paquetes de ondas. Obsérvese también que los paquetes de ondas, es decir, las amplias regiones de grandes amplitudes positivas y negativas, se mueven hacia la derecha con el aumento del tiempo también.
Dado que la velocidad es la distancia desplazada Δ\(x \) dividida por el tiempo transcurrido Δ\(t\), la pendiente de una línea en la figura 1.16, Δ\(t∕\) Δ\(x\), es una sobre la velocidad de lo que sea que esa línea represente. Las pendientes de las líneas que representan crestas son las mismas que las pendientes de las líneas que representan paquetes de ondas en este caso, lo que indica que las dos se mueven a la misma velocidad. Dado que la velocidad de movimiento de las crestas de onda es la velocidad de fase y la velocidad de movimiento de los paquetes de ondas es la velocidad de grupo, las dos velocidades son iguales y se confirma la naturaleza no dispersiva de este caso.
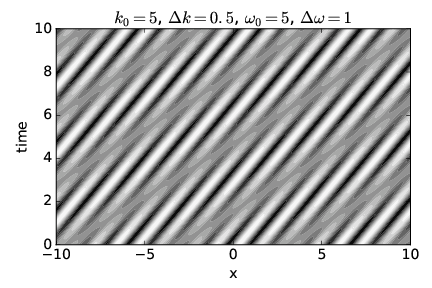
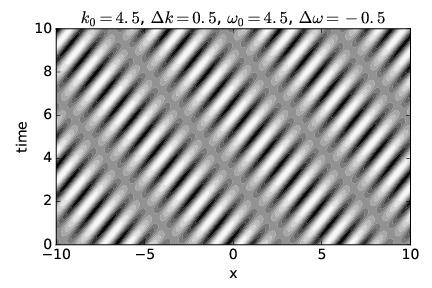
La figura 1.17 muestra una onda dispersiva en la que la velocidad del grupo es el doble de la velocidad de fase, mientras que la figura 1.18 muestra un caso en el que la velocidad del grupo es realmente opuesta en signo a la velocidad de fase. Vea si puede confirmar que las velocidades de fase y grupo vistas en cada figura corresponden a los valores para estas cantidades calculadas a partir de las frecuencias y números de onda especificados.
Problemas
- Mida su frecuencia de pulso. Calcula la frecuencia ordinaria de tus latidos cardíacos en ciclos por segundo. Calcular la frecuencia angular en radianes por segundo. Calcula el periodo.
- Una longitud de onda importante para las ondas de radio en radioastronomía es de 21 cm. (Esto viene del hidrógeno neutro.) Calcular el número de onda de esta ola. Calcular las frecuencias ordinarias y angulares. (La velocidad de la luz es de 3 × 10 8 m s - 1.)
- Esboza la onda resultante obtenida al superponer las ondas\(A \) = sin (2\(x\)) y\(B \) = sin (3\(x\)). Mediante el uso de la identidad trigonométrica dada en la ecuación 1.17}, obtener una fórmula para\(A\) +\(B \) en términos de sin (5\(x∕\) 2) y cos (\(x∕\)2). ¿La onda obtenida al dibujar esta fórmula concuerda con tu boceto anterior?
- }
- Dos ondas sinusoidales con longitudes de onda\(λ\) 1 y\(λ\) 2 se superponen, haciendo paquetes de onda de longitud\(L\). Si queremos hacer\(L \) más grandes, ¿deberíamos hacer\(λ\) 1 y\(λ\) 2 más cerca o más separados? Explica tu razonamiento.
- Al examinar la figura 1.9 versus la figura 1.10 y luego la figura 1.11 versus la figura 1.12, determinar si la ecuación 1.18} funciona al menos en un sentido aproximado para paquetes de ondas aisladas.
- }
- Las frecuencias de la escala cromática en la música están dadas por
- \[fi = f02i∕12, i = 0,1,2,...,11, " class="math-display" src="/book143x.png\label{1.42}\]
donde\(f\) 0 es una constante igual a la frecuencia de la nota más baja en la escala.
- Calcular del\(f\) 1 al\(f\) 11 si\(f\) 0 = 440 Hz (la nota “A”).
- Usando los resultados anteriores, ¿cuál es la frecuencia de latido entre las notas “A” (\(i \)= 0) y “B” (\(i \)= 2)? (Las frecuencias se dan aquí en ciclos por segundo en lugar de radianes por segundo).
- ¿Qué par de las frecuencias anteriores\(f\) 0 -\(f\) 11 produce la frecuencia de latido más pequeña? Explica tu razonamiento.
Figura 1.19: Croquis de un radar policial.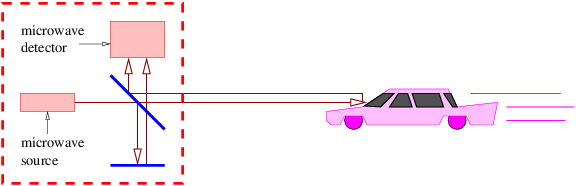
_____________________________________
- Los barcos grandes en general no pueden moverse más rápido que la velocidad de fase de las olas superficiales con una longitud de onda igual al doble de la longitud del barco. Esto se debe a que la mayor parte de la fuerza propulsiva va a hacer grandes olas bajo estas condiciones en lugar de acelerar el barco.
- ¿Qué tan rápido puede moverse un barco de 300 m de largo en aguas muy profundas?
- A medida que el barco se mueve hacia aguas poco profundas, ¿aumenta o disminuye su velocidad máxima? Explique.
- Dada la fórmula para el índice de refracción de la luz citada en esta sección, ¿para qué rango de\(k \) la velocidad de fase de la luz en un material transparente adquiere valores reales que superan la velocidad de la luz en un vacío?
- Un radar policial funciona dividiendo un haz de microondas, parte del cual se refleja de nuevo al radar desde tu auto donde se hace interferir con la otra parte que recorre un camino fijo, como se muestra en la figura 1.19.
- Si la longitud de onda de las microondas es\(λ\), ¿qué tan lejos tiene que viajar en su automóvil para que la interferencia entre los dos haces pase de constructiva a destructiva a constructiva?
- Si viaja hacia el radar a velocidad\(v \) = 30 m s - 1, use el resultado anterior para determinar el número de veces por segundo que se producirán picos de interferencia constructiva. Supongamos que\(λ \) = 3 cm.
Figura 1.20: Croquis de un interferómetro Fabry-Perot.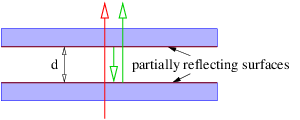
_____________________________________
- Supongamos que conoce la longitud de onda de la luz que pasa por un interferómetro Michelson con alta precisión. Describe cómo podrías usar el interferómetro para medir la longitud de una pequeña pieza de material.
- Un interferómetro Fabry-Perot (ver figura 1.20) consiste en dos espejos semiplateados paralelos colocados a una\(d \) distancia uno del otro como se muestra. El haz que pasa directamente interfiere con el haz que se refleja una vez fuera de ambas superficies reflejadas como se muestra. Para longitud de onda\(λ\), ¿qué valores de\(d \) resultado en interferencia constructiva?
- Un interferómetro Fabry-Perot tiene espaciamiento\(d \) = 2 cm entre las placas de vidrio, provocando que los haces directos y doblemente reflejados interfieran (ver figura 1.20). A medida que el aire es bombeado fuera del hueco entre las placas, los haces pasan por 23 ciclos de interferencia constructiva-destructiva-constructiva. Si la longitud de onda de la luz en los haces interferentes es de 5 × 10 - 7 m, determinar el índice de refracción del aire inicialmente en el interferómetro.
- Las mediciones en cierto tipo de onda revelan que la frecuencia angular de la onda varía con el número de onda como se muestra en la siguiente tabla:
\(ω \)(s - 1)\(k \) (m - 1) 5 1 20 2 45 3 80 4 125 5
- Calcular la velocidad de fase de la ola para\(k \) = 3 m - 1 y para\(k \) = 4 m - 1.
- Estimar la velocidad del grupo para\(k \) = 3\(.\) 5 m - 1 usando una aproximación de diferencia finita a la derivada.
- Supongamos que algún tipo de onda tiene la relación de dispersión (sin duda extraña) mostrada en la figura 1.21.
- ¿Para qué valores de\(k \) la velocidad de fase de la onda es positiva?
- ¿Para qué valores de la velocidad del grupo\(k \) es positiva?
Figura 1.21: Croquis de una extraña relación de dispersión.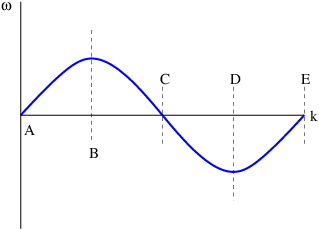
_____________________________________
- Velocidades de grupo de varias olas.
- Calcular la velocidad del grupo para olas de aguas poco profundas. Compárela con la velocidad de fase de las olas de aguas poco profundas. (Pista: Primero necesita derivar una fórmula para\(ω\) (\(k\)) de\(c\) (\(k\)).)
- Repita el problema anterior para las olas de aguas profundas.
- Repita para las ondas sonoras. ¿Qué tiene en común este caso con las olas de aguas poco profundas?
Capítulo 2 Olas en Dos y Tres Dimensiones
En este capítulo extendemos las ideas del capítulo anterior al caso de las olas en más de una dimensión. La extensión de la onda sinusoidal a dimensiones más altas es la onda plana. Los paquetes de ondas en dos y tres dimensiones surgen cuando se superponen ondas planas que se mueven en diferentes direcciones.
La difracción es el resultado de la interrupción de una onda que incide sobre un objeto. Aquellas partes del frente de onda que golpean el objeto son dispersas, modificadas o destruidas. El patrón de difracción resultante proviene de la posterior interferencia de las diversas piezas de la onda modificada. Un conocimiento de la difracción es necesario para comprender el comportamiento y las limitaciones de los instrumentos ópticos como los telescopios.
La difracción e interferencia en dos y tres dimensiones se pueden manipular para producir dispositivos útiles como la rejilla de difracción.
Tutorial — Vectores
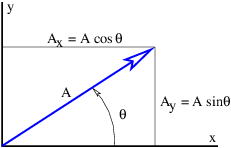
Antes de continuar, necesitamos explorar la idea de un vector. Un vector es una cantidad que expresa tanto la magnitud como la dirección. Gráficamente representamos un vector como una flecha. En la notación de tipografía un vector está representado por un carácter de negrita, mientras que en escritura a mano se dibuja una flecha sobre el carácter que representa el vector.
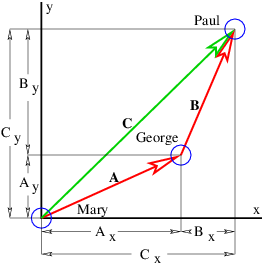
La Figura 2.1 muestra algunos ejemplos de vectores de desplazamiento, es decir, vectores que representan el desplazamiento de un objeto de otro, e introduce la idea de adición de vectores. La cola del vector\(B\) se coloca con la cabeza del vector\(A\), y el vector que se extiende desde la cola de\(A\) a la cabeza de\(B\) es la suma de\(A\) y\(B\), llamado\(C\) en la figura 2.1.
Las cantidades\(A\) x,\(A\) y, etc., representan los componentes cartesianos de los vectores en la figura 2.1. Un vector se puede representar ya sea por sus componentes cartesianos, que son solo las proyecciones del vector sobre los ejes de coordenadas cartesianas, o por su dirección y magnitud. La dirección de un vector en dos dimensiones generalmente se representa por el ángulo en sentido contrario a las agujas del reloj del vector con respecto al\(x\) eje, como se muestra en la figura 2.2. La conversión de una forma a otra viene dada por las ecuaciones
\[A = (A2x + A2y)1∕2 θ = tan- 1(Ay ∕Ax ), \label{2.2}\]
donde\(A \) está la magnitud del vector. Una magnitud vectorial a veces se representa por notación de valor absoluto:\(A \) º |\(A\) |.
Observe que la tangente inversa da un resultado que es ambiguo relativo a sumar o restar múltiplos enteros de\(π\). Así, el cuadrante en el que se encuentra el ángulo debe resolverse examinando independientemente los signos de\(A\) x e\(A\) y y eligiendo el valor apropiado de\(θ\).
Para agregar dos vectores,\(A\) y\(B\), es más fácil convertirlos a forma de componente cartesiano. Los componentes de la suma\(C\) =\(A\) +\(B\) son entonces solo las sumas de los componentes:
\[Cx = Ax + Bx Cy = Ay + By. \label{2.3}\]
La resta de vectores se realiza de manera similar, por ejemplo, si\(A\) =\(C\) -\(B\), entonces
\[Ax = Cx - Bx Ay = Cy - By. \label{2.4}\]
Un vector unitario es un vector de longitud unitaria. Siempre se puede construir un vector unitario a partir de un vector ordinario (distinto de cero) dividiendo el vector por su longitud:\(n\) =\(A\)\(∕\) |\(A\) |. Esta operación de división se lleva a cabo dividiendo cada uno de los componentes vectoriales por el número en el denominador. Alternativamente, si el vector se expresa en términos de longitud y dirección, la magnitud del vector se divide por el denominador y la dirección no cambia.
Los vectores unitarios se pueden utilizar para definir un sistema de coordenadas cartesianas. Convencionalmente\(i\)\(j\),,, e\(k\) indicar los\(x\)\(z \) ejes\(y\),, y de dicho sistema. Tenga en cuenta que\(i\)\(j\),, y\(k\) son mutuamente perpendiculares. Cualquier vector puede ser representado en términos de vectores unitarios y sus componentes cartesianos:\(A\) =\(A\) x\(i\) +\(A\) y\(j\) +\(A\) z\(k\). Una forma alternativa de representar un vector es como una lista de componentes:\(A\) = (\(A\)x\(,A\) y\(,A\) z). Tendemos a utilizar esta última representación ya que es una notación algo más económica.
Hay dos formas de multiplicar dos vectores, produciendo respectivamente lo que se conoce como el producto punto y el producto cruzado. El producto cruzado produce otro vector mientras que el producto de punto produce un número. Aquí discutiremos solo el producto punto. El producto cruzado se presentará más adelante cuando sea necesario.
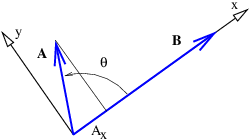
Dados vectores\(A\) y\(B\), el producto de punto de los dos se define como
\[A ⋅ B ≡ |A ||B |cosθ, \label{2.5}\]
donde\(θ \) está el ángulo entre los dos vectores. En dos dimensiones existe una expresión alternativa para el producto punto en términos de los componentes cartesianos de los vectores:
\[A ⋅ B = AxBx + AyBy. \label{2.6}\]
Es fácil demostrar que esto es equivalente a la forma coseno del producto de punto cuando el\(x \) eje se encuentra a lo largo de uno de los vectores, como en la figura 2.3. Observe en particular que\(A\) x = |\(A\) | cos\(θ\), mientras que\(B\) x = \(B\)| | e\(B\) y = 0. Así,\(A\) ⋅\(B\) = |\(A\) | cos\(θ\) |\(B\) | en este caso, que es idéntica a la forma dada en la ecuación 2.5}.
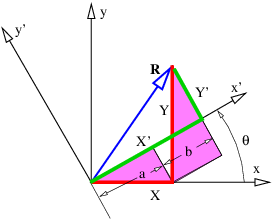
Todo lo que queda por probar para que la ecuación 2.6} sostenga en general es mostrar que produce la misma respuesta independientemente de cómo se orienta el sistema de coordenadas cartesianas en relación con los vectores. Para ello, debemos mostrar que\(A\) x\(B\) x +\(A\) y\(B\) y =\(A\) x ′\(B\) x ′ +\(A\) y ′\(B\) y ′, donde los primos indican componentes en un sistema de coordenadas girado desde el sistema de coordenadas original.
La Figura 2.4 muestra el vector\(R\) resuelto en dos sistemas de coordenadas girados uno con respecto al otro. A partir de esta cifra queda claro que\(X\) ′ =\(a \) +\(b\). Centrándonos en los triángulos sombreados, vemos que\(a \) =\(X\) cos\(θ \) y\(b \) =\(Y\) pecado\(θ\). Así, encontramos\(X\) ′ =\(X\) cos\(θ \) +\(Y\) pecado\(θ\). Razonamiento similar muestra que\(Y \) ′ = -\(X\) sin\(θ \) +\(Y\) cos\(θ\). Sustituyendo estos y usando la identidad trigonométrica cos 2\(θ \) + sin 2\(θ \) = 1 da como resultado
\[ ′ ′ ′ ′ A xB x + AyB y = (Ax cos θ + Ay sin θ)(Bx cosθ + By sin θ) + (- Ax sinθ + Ay cos θ)(- Bx sinθ + By cos θ) = AxBx + AyBy \label{2.7} \]
demostrando así la equivalencia completa de las dos formas del producto punto según lo dado por las ecuaciones (2.5) y (2.6). Multiplique la expresión anterior para verificar esto.
Una cantidad numérica que no depende del sistema de coordenadas que se esté utilizando se llama escalar. El producto punto de dos vectores es un escalar. Sin embargo, los componentes de un vector, tomados individualmente, no son escalares, ya que los componentes cambian a medida que cambia el sistema de coordenadas. Dado que las leyes de la física no pueden depender de la elección del sistema de coordenadas que se utilice, insistimos en que las leyes físicas se expresen en términos de escalares y vectores, pero no en términos de los componentes de los vectores.
En tres dimensiones la forma coseno del producto punteado sigue siendo la misma, mientras que la forma del componente es
\[A ⋅ B = AxBx + AyBy + AzBz. \label{2.8}\]
Ondas Planas
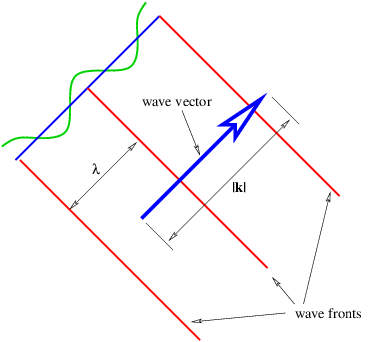
Una onda plana en dos o tres dimensiones es como una onda sinusoidal en una dimensión, excepto que las crestas y valles no son puntos, sino que forman líneas (2-D) o planos (3-D) perpendiculares a la dirección de propagación de la onda. La Figura 2.5 muestra una onda sinusoidal plana en dos dimensiones. La flecha grande es un vector llamado vector de onda, que define (1) la dirección de propagación de la onda por su orientación perpendicular a los frentes de onda, y (2) el número de onda por su longitud. Podemos pensar en un frente de ola como una línea a lo largo de la cresta de la ola. La ecuación para el desplazamiento asociado a una onda sinusoidal plana (de amplitud unitaria) en tres dimensiones en algún instante en el tiempo es
\[h(x,y, z) = sin(k ⋅ x ) = sin(kxx + kyy + kzz ). \label{2.9}\]
Dado que los frentes de onda son líneas o superficies de fase constante, la ecuación que define un frente de onda es simplemente\(k\) ⋅\(x\) =\(const\).
En el caso bidimensional simplemente establecemos\(k\) z = 0. Por lo tanto, un frente de onda, o línea de fase constante\(ϕ \) en dos dimensiones se define por la ecuación
\[k ⋅ x = kxx + kyy = ϕ (two dimensions ). \label{2.10}\]
Esto se puede resolver fácilmente\(y \) para obtener la pendiente e intercepción del frente de ola en dos dimensiones.
En cuanto a las ondas unidimensionales, la evolución temporal de la onda se obtiene agregando un término -\(ωt \) a la fase de la onda. En tres dimensiones el desplazamiento de onda en función tanto del espacio como del tiempo viene dado por
\[h (x,y,z,t) = sin (kxx + kyy + kzz - ωt). \label{2.11}\]
La frecuencia depende en general de los tres componentes del vector de onda. La forma de esta función,\(ω \) =\(ω\) (\(k\)x\(,k\) y\(,k\) z), que como en el caso unidimensional se denomina relación de dispersión, contiene información sobre la física comportamiento de la ola.
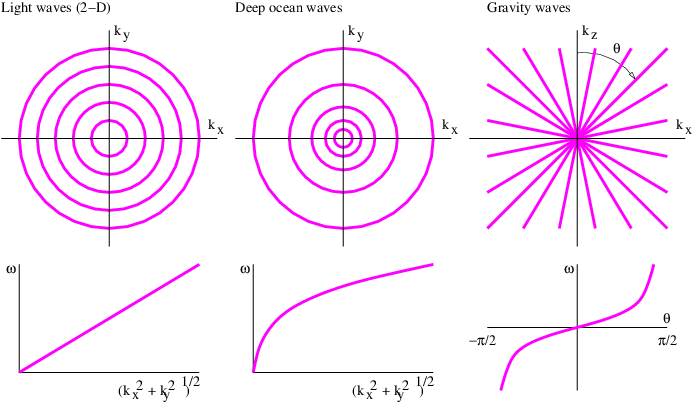
Algunos ejemplos de relaciones de dispersión para olas en dos dimensiones son los siguientes:
- Obedecen las ondas de luz en un vacío en dos dimensiones
- \[ω = c(k2x + k2y)1∕2 (light), " class="math-display" src="/book155x.png\label{2.12}\]
donde\(c \) esta la velocidad de la luz en un vacio.
- Olas oceánicas de aguas profundas en dos dimensiones obedecen
- \[ω = g1∕2(k2x + k2y)1∕4 (ocean waves), " class="math-display" src="/book156x.png\label{2.13}\]
donde\(g \) está la fuerza del campo gravitacional de la Tierra como antes.
- Ciertos tipos de ondas atmosféricas confinadas a un\(z \) plano vertical\(x\) llamado ondas gravitacionales (que no deben confundirse con las ondas gravitacionales de la relatividad general) 1 obedecen
- \[ω = N-kx- (gravity waves ), kz \label{2.14}\]
donde\(N \) es una constante con las dimensiones del tiempo inverso llamada la frecuencia Brunt-Väisälä.
Las gráficas de contorno de estas relaciones de dispersión se trazan en los paneles superiores de la figura 2.6. Estas parcelas deben interpretarse como mapas topográficos, donde las líneas representan contornos de elevación constante. En el caso de la figura 2.6, se representan en su lugar valores constantes de frecuencia. Por simplicidad, los valores reales de frecuencia no están etiquetados en las gráficas de contorno, sino que se representan en las gráficas en los paneles inferiores. Esto es posible porque la frecuencia depende únicamente de la magnitud del vector de onda (\(k\)x 2 +\(k\) y 2 ) 1 2 para los dos primeros ejemplos, y sólo en la dirección del vector de onda\(θ \) para el tercero.
Superposición de Ondas Planas
Ahora estudiamos paquetes de ondas en dos dimensiones preguntándonos cómo es la superposición de dos ondas sinusoidales planas. Si las dos ondas tienen números de onda diferentes, pero sus vectores de onda apuntan en la misma dirección, los resultados son idénticos a los presentados en el capítulo anterior, excepto que los paquetes de ondas se alargan indefinidamente sin cambio de forma en la dirección perpendicular al vector de onda. Los paquetes de ondas producidos en este caso se mueven en la dirección de los vectores de onda y así aparecen a un observador estacionario como una serie de pulsos pasantes con amplia extensión lateral.
La superposición de dos ondas planas que tienen la misma frecuencia da como resultado un paquete de ondas estacionarias a través del cual pasan los frentes de onda individuales. Este paquete de ondas también se alarga indefinidamente en alguna dirección, pero la dirección del alargamiento depende de la relación de dispersión para las ondas que se están considerando. Estos paquetes de ondas están en forma de haces constantes, que guían las ondas de fase individuales en alguna dirección, pero no cambian por sí mismas con el tiempo. Al superponer múltiples ondas planas, todas con la misma frecuencia, en realidad se puede producir un solo haz estacionario, así como se puede producir un pulso aislado superponiendo múltiples ondas con vectores de onda apuntando en la misma dirección.
Si la frecuencia de una onda depende de la magnitud del vector de onda, pero no de su dirección, la relación de dispersión de la onda se denomina isotrópica; de lo contrario, es anisotrópica. En el caso isotrópico, dos ondas tienen la misma frecuencia solo si las longitudes de sus vectores de onda, y de ahí sus longitudes de onda, son las mismas. Los dos primeros ejemplos de la figura 2.6 satisfacen esta condición, mientras que el último es anisotrópico.
Ahora utilizamos el lenguaje de vectores para investigar la superposición de dos ondas planas con los vectores de onda\(k\) 1 y\(k\) 2:
\[h = sin(k1 ⋅ x - ωt ) + sin(k2 ⋅ x - ωt). \label{2.15}\]
Aplicando la identidad trigonométrica para el seno de la suma de dos ángulos (como hemos hecho anteriormente), la ecuación 2.15} se puede reducir a
\[h = 2 sin (k0 ⋅ x - ωt)cos(Δk ⋅ x) \label{2.16}\]
donde
\[k0 = (k1 + k2 )∕2 Δk = (k2 - k1)∕2. \label{2.17}\]
Esto es en forma de onda sinusoidal que se mueve en la dirección\(k\) 0 con velocidad de\(c\) fase fase =\(ω∕\) |\(k\) 0 | y número de onda |\(k\) 0 |, modulada en la\(k\) dirección Δ por una función coseno. Las líneas de interferencia destructiva son normales a Δ\(k\). La distancia\(w\) entre líneas de interferencia destructiva es la distancia entre ceros sucesivos de la función coseno en la ecuación 2.16}, lo que implica que | Δ\(k\) |\(w \) =\(π\), lo que lleva a
\[w = π∕|Δk |. \label{2.18}\]
Así, cuanto menor | Δ\(k\) |, mayor es el diámetro del haz.
Ondas de longitud de onda idéntica
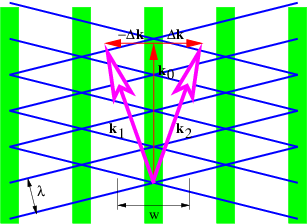
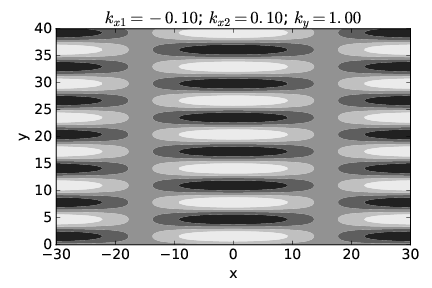
En esta sección investigamos los haces producidos por la superposición de ondas isotrópicas de la misma frecuencia. La Figura 2.7 ilustra lo que sucede en tal superposición. Los vectores\(k\) 1 y\(k\) 2 de igual longitud dan lugar a un vector de onda media\(k\) 0 y la mitad de la diferencia, Δ\(k\). Como se ilustra, las líneas de interferencia constructiva y destructiva son perpendiculares a Δ\(k\). La Figura 2.8 muestra un ejemplo concreto de los haces producidos por superposición de dos ondas planas de igual longitud de onda orientadas como en la figura 2.7. Los haces están alineados verticalmente, ya que Δ\(k\) es horizontal, con las líneas de interferencia destructiva que separan los haces ubicados cerca de\(x \) = ± 16. El ancho transversal de las vigas de ≈ 32 satisface la ecuación 2.18} con | Δ\(k\) | = 0\(.\) 1. Cada haz está formado por ondas de fase que se propagan verticalmente, con las crestas y canales indicados por las regiones de blanco y negro.
Ondas de diferente longitud de onda
En el tercer ejemplo de la figura 2.6, la frecuencia de la onda depende únicamente de la dirección del vector de onda, independientemente de su magnitud, que es lo contrario del caso para una relación de dispersión isotrópica. En este caso altamente anisotrópico, diferentes ondas planas con la misma frecuencia tienen vectores de onda que apuntan en la misma dirección, pero tienen diferentes longitudes.
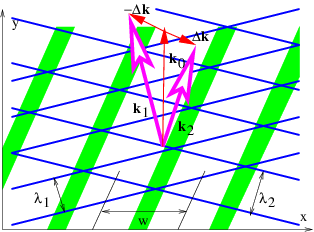
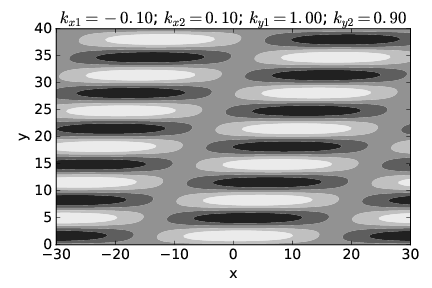
De manera más general, uno podría tener ondas para las cuales la frecuencia depende tanto de la dirección como de la magnitud del vector de onda. En este caso, dos ondas planas diferentes con la misma frecuencia normalmente tendrían vectores de onda que difieren tanto en dirección como en magnitud. Tal ejemplo se ilustra en las figuras 2.9 y 2.10.

La Figura 2.11 resume lo que hemos aprendido sobre la adición de ondas planas con la misma frecuencia. En general, la orientación del haz (y las líneas de interferencia constructiva) no son perpendiculares a los frentes de onda. Esto solo ocurre cuando la frecuencia de onda es independiente de la dirección del vector de onda.
Ondas con la misma longitud de onda
Al igual que con los paquetes de ondas en una dimensión, podemos sumar más de dos ondas para producir un paquete de ondas aisladas. Aquí limitaremos nuestra atención al caso de una relación de dispersión isotrópica en la que todos los vectores de onda para una frecuencia dada son de la misma longitud.
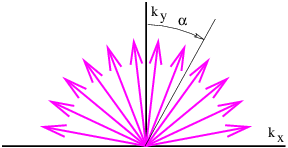
La Figura 2.12 muestra un ejemplo de esto en el que se suman vectores de onda de la misma longitud de onda pero diferentes direcciones. Definiendo\(α\) i como el ángulo del vector de onda\(i\) th en sentido horario desde la vertical, como se ilustra en la figura 2.12, podríamos escribir la superposición de estas ondas en el tiempo\(t \) = 0 como
\[h = ∑ h sin(k x + k y) i i xi yi ∑ = hisin[kx sin(αi) + ky cos(αi )\label{2.19}\]i\]
donde hemos asumido que\(k\) xi =\(k\) sin (\(α\)i) y\(k\) yi =\(k\) cos (\(α\)i). El parámetro\(k \) = |\(k\) | es la magnitud del vector de onda y es el mismo para todas las ondas. Supongamos también en este ejemplo que la amplitud de cada componente de onda disminuye al aumentar |\(α\) i |:
\[hi = exp[- (αi∕ αmax)2]. \label{2.20}\]
La función exponencial disminuye rápidamente a medida que su argumento se vuelve más negativo, y para fines prácticos, solo los vectores de onda con |\(α\) i |≤\(α\) max contribuyen significativamente a la suma. Llamamos a\(α\) max el ángulo de esparcimiento.
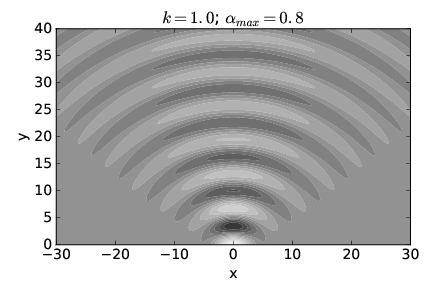
La Figura 2.13 muestra cómo se ve\(h\) (\(x,y\)) cuando\(α\) max = 0\(.\) 8 radianes y\(k \) = 1. Observe que para\(y \) = 0 la amplitud de onda solo es grande para una región pequeña en el rango - 4\(< x < \) 4. Sin embargo, para\(y > \) 0 la onda se extiende en un patrón ancho y semicircular.
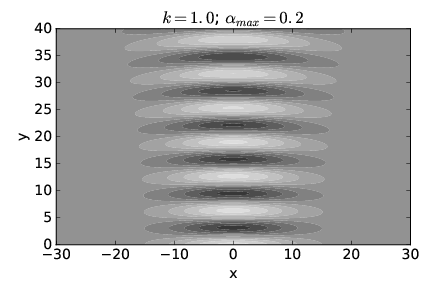
La Figura 2.14 muestra el patrón calculado de\(h\) (\(x,y\)) cuando el ángulo de dispersión\(α\) max = 0\(.\) 2 radianes. La amplitud de onda es grande para un rango mucho más amplio de\(x\) at\(y \) = 0 en este caso, aproximadamente - 12\(< x < \) 12. Por otro lado, la propagación posterior de la ola es mucho menor que en el caso de la figura 2.13.
Concluimos que una superposición de ondas planas con vectores de onda extendidos estrechamente alrededor de un vector de onda central que apunta en la\(y \) dirección (como en la figura 2.14) produce un haz que inicialmente es ancho\(x \) pero para el cual la anchura aumenta solo ligeramente con el aumento\(y\). Sin embargo, una superposición de ondas planas con vectores de onda extendidos más ampliamente (como en la figura 2.13) produce un haz que inicialmente es estrecho\(x \) pero que aumenta rápidamente en anchura a medida que\(y\) aumenta.
La relación entre el ángulo\(α\) máximo de dispersión y la anchura inicial del haz se hace más comprensible en comparación con los resultados de la superposición de dos ondas discutidos al inicio de esta sección. Como lo indica la ecuación 2.18}, los valores grandes de\(k\) x, y por lo tanto\(α\), están asociados con dimensiones de paquetes de onda pequeña en la\(x \) dirección y viceversa. La superposición de dos ondas no captura la propagación posterior del haz que ocurre cuando se superponen muchas ondas, pero sí conduce a una relación cuantitativa aproximada entre\(α\) max (que es solo bronceado - 1 ( \(k\)x\(∕k\) y) en el caso de dos ondas) y la anchura inicial del haz. Si invocamos la aproximación de ángulo pequeño para\(α \) =\(α\) max para que\(α\) max = tan - 1 (\(k\)x\(∕k\) y) ≈\(k\) x\(∕k\) y ≈\(k\) x\(∕k\), luego\(k\) x ≈\(kα\) max y ecuación (2.18) se puede escribir\(w \) =\(π∕k\) x ≈\(π∕\) (\(kα\)max) =\(λ∕\) (2\(α\) max). Así, podemos encontrar el ángulo de dispersión aproximado a partir de la longitud de onda de la onda\(λ \) y la anchura inicial del haz\(w\):
\[αmax ≈ λ∕(2w ) (single slit spreading angle). \label{2.21}\]
Difracción a través de una sola rendija
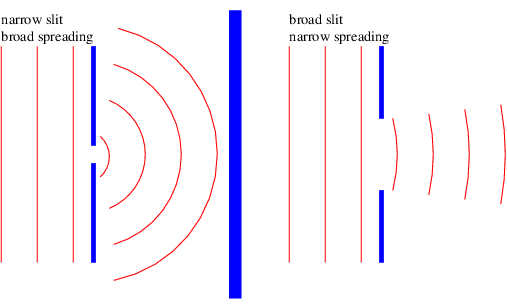
¿Cómo se aplica todo esto al paso de las olas por una hendidura? Imagina una onda plana de longitud de onda que\(λ \) incide sobre una barrera con una hendidura. La barrera transforma la onda plana con extensión infinita en dirección lateral en una viga con dimensiones transversales iniciales iguales al ancho de la hendidura. El desarrollo posterior del haz se ilustra en las figuras 2.13 y 2.14, y esquemáticamente en la figura 2.15. En particular, si la anchura de la hendidura es comparable a la longitud de onda, el haz se extiende ampliamente como en la figura 2.13. Si el ancho de la hendidura es grande en comparación con la longitud de onda, el haz no se propaga tanto, como ilustra la figura 2.14. La ecuación (2.21) nos da un resultado cuantitativo aproximado para el ángulo de dispersión si\(w \) se interpreta como el ancho de la hendidura.
Un uso de la ecuación anterior es para determinar la resolución angular máxima de instrumentos ópticos como telescopios. La lente primaria o el espejo se puede considerar como una “hendidura” bastante grande. La luz de una fuente puntual distante es esencialmente en forma de onda plana cuando llega al telescopio. Sin embargo, la luz que pasa por el telescopio ya no es una onda plana, sino un haz con tendencia a propagarse. El ángulo\(α\) máximo de dispersión viene dado por la ecuación (2.21), y el telescopio no puede resolver objetos con una separación angular inferior a\(α\) máx. Reemplazar\(w \) con el diámetro de la lente o espejo en la ecuación (2.21) produce así la resolución angular del telescopio. Por ejemplo, un telescopio de tamaño moderado con apertura de 1 m observando luz roja con\(λ \) ≈ 6 × 10 - 7 m tiene una resolución angular máxima de aproximadamente 3 × 10 - 7 radianes.
Fallas
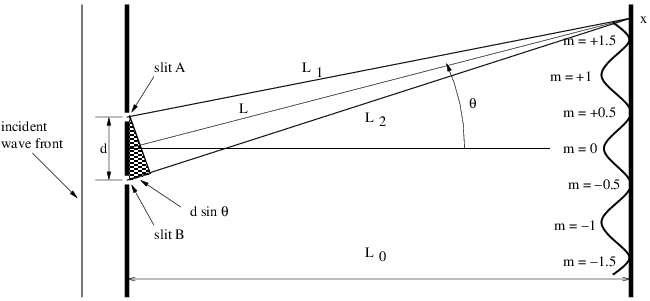
Imaginemos ahora una onda sinusoidal plana que normalmente incide sobre una pantalla con dos hendiduras estrechas espaciadas por una distancia\(d\), como se muestra en la figura 2.16. Dado que las hendiduras son estrechas en relación con la longitud de onda de la onda que incide sobre ellas, el ángulo de dispersión de los haces es grande y el patrón de difracción de cada hendidura individualmente es una onda cilíndrica que se extiende en todas las direcciones, como se ilustra en la figura 2.13. Las ondas cilíndricas de las dos hendiduras interfieren, dando como resultado oscilaciones en la intensidad de onda en la pantalla del lado derecho de la figura 2.16.
La interferencia constructiva ocurre cuando la diferencia en las trayectorias recorridas por las dos ondas desde sus ranuras de origen hasta la pantalla,\(L\) 2 -\(L\) 1, es un múltiplo entero\(m \) de la longitud de onda\(λ\): \(L\)2 -\(L\) 1 =\(mλ\). Si\(L\) 0 ≫\(d\), las líneas\(L\) 1 y\(L\) 2 son casi paralelas, lo que significa que el extremo estrecho del triángulo oscuro en la figura 2.16 tiene un ángulo de apertura de\(θ\). Así, la diferencia de trayectoria entre las vigas de las dos hendiduras es\(L\) 2 -\(L\) 1 =\(d\) sin\(θ\). La sustitución de esto en la ecuación anterior muestra que la interferencia constructiva ocurre cuando
\[d sinθ = m λ, m = 0,±1, ±2, ... (two slit interference). \label{2.22}\]
La interferencia destructiva ocurre cuando\(m \) es un entero más 1\(∕\) 2. El entero\(m \) se llama orden de interferencia y es el número de longitudes de onda por las que difieren las dos trayectorias.
Rejillas de difracción
Dado que el espaciamiento angular Δ\(θ \) de los picos de interferencia en el caso de dos hendiduras depende de la longitud de onda de la onda incidente, el sistema de dos hendiduras se puede usar como un dispositivo crudo para distinguir entre las longitudes de onda de diferentes componentes de una onda no sinusoidal que incide en las ranuras. Sin embargo, si se agregan más hendiduras, manteniendo un espaciado uniforme\(d \) entre hendiduras, obtenemos un dispositivo más sofisticado para distinguir los componentes de la viga. Esto se llama rejilla de difracción.
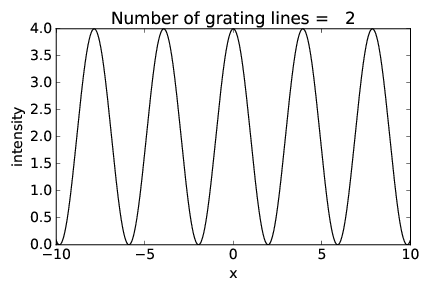
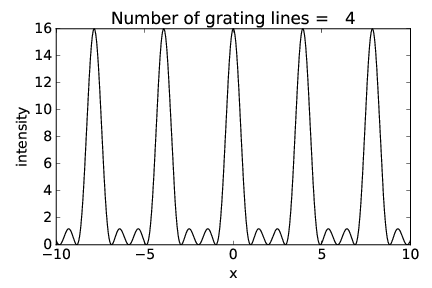
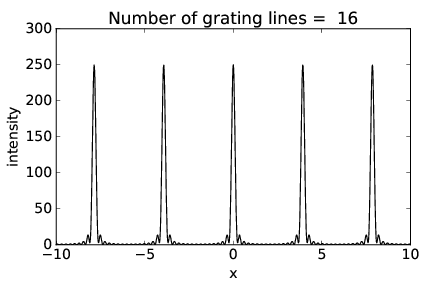
Las figuras 2.17-2.19 muestran la intensidad del patrón de difracción en función de la posición\(x \) en la pantalla de visualización (ver figura 2.16) para rejillas con 2, 4 y 16 hendiduras respectivamente, con el mismo espaciado de rendijas. Observe cómo los picos de interferencia permanecen en el mismo lugar pero aumentan en nitidez a medida que aumenta el número de ranuras.
El ancho de los picos está realmente relacionado con el ancho total de la rejilla,\(w \) =\(nd\), donde\(n \) está el número de hendiduras. Pensando en este ancho como la dimensión de una sola hendidura grande, la ecuación de hendidura única,\(α\) max =\(λ∕\) (2\(w\)), nos dice el ancho angular de los picos. 2
Mientras que el ancho angular de los picos de interferencia se rige por la ecuación de hendidura única, sus posiciones angulares están gobernadas por la ecuación de dos hendiduras. Supongamos por simplicidad que |\(θ\) |1 para que podamos hacer la aproximación de ángulo pequeño a la ecuación de dos rendijas,\(mλ \) =\(d\) sin\(θ \) ≈\(dθ\), y hacer la siguiente pregunta: ¿Qué tan diferentes hacen dos longitudes de onda que difieren en Δ \(λ \)tiene que ser para que los picos de interferencia de las dos ondas no se superpongan? Para que los picos sean distinguibles, deben estar separados\(θ \) por un ángulo Δ\(θ \) =\(m\) Δ\(λ∕d\), que es mayor que el ancho angular de cada pico,\(α\) max:
\[Δ θ \]αmax. "class="math-display” src=” /book166x.png “> (2.23)
Sustituyendo en las expresiones anteriores por Δ\(θ \) y\(α\) max y resolviendo por Δ\(λ\), obtenemos Δ\(λ > λ∕\) (2\(mn\)), donde\(λ \) es el promedio de las dos longitudes de onda y\(n \) =\(w∕d \) es el número de ranuras en la rejilla de difracción. Así, la diferencia fraccionaria entre longitudes de onda que pueden distinguirse mediante una rejilla de difracción depende únicamente del orden de interferencia\(m \) y del número de hendiduras\(n \) en la rejilla:
\[Δ-λ- -1--- λ \]2mn. "class="math-display” src=” /book167x.png “> (2.24)
Problemas
- El punto A está en el origen. El punto B está a 3 m de distancia de A a 30 ° en sentido antihorario del\(x \) eje. El punto C está a 2 m del punto A a 100 ° en sentido antihorario desde el\(x \) eje.
- Obtener los componentes cartesianos del vector\(D\) 1 que va de A a B y el vector\(D\) 2 que va de A a C.
- Encuentra los componentes cartesianos del vector\(D\) 3 que va de B a C.
- Encuentra la dirección y magnitud de\(D\) 3.
Figura 2.20: Croquis de onda moviéndose a 45° con respecto al\(x\) eje.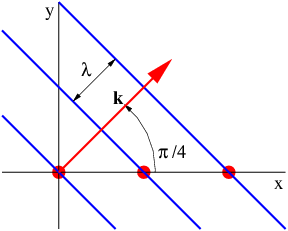
_____________________________________
- Para los vectores en el problema anterior, encuentra\(D\) 1 ⋅\(D\) 2 usando tanto la forma coseno del producto punto como la forma cartesiana. Comprueba si las dos respuestas son las mismas.
- Mostrar gráficamente o de otra manera que |\(A\) +\(B\) \(≠\)|\(A\) | | | +\(B\) | | excepto cuando los vectores\(A\) y\(B\) son paralelos.
- Una onda en el\(y \) plano\(x\) - se define por\(h \) =\(h\) 0 sin (\(k\)⋅\(x\)) donde\(k\) = (1\(, \) 2) cm - 1.
- En un trozo de papel cuadriculado dibujar\(x \) y\(y \) ejes y luego trazar una línea que pasa por el origen que es paralela al vector\(k\).
- En la misma gráfica grafica la línea definida por\(k\) ⋅\(x\) =\(k\) x\(x \) +\(k\) y\(y \) = 0,\(k\) ⋅\(x\) =\(π\), y\(k\) ⋅\(x\) = 2 \(π\). Verifique si estas líneas son perpendiculares a\(k\).
- Una onda plana en dos dimensiones en el\(y \) plano\(x \) - se mueve en la dirección 45 ° en sentido contrario a las agujas del reloj desde el\(x\) eje -como se muestra en la figura 2.20. Determinar qué tan rápido se mueve la intersección entre un frente de ola y el\(x\) eje -eje hacia la derecha en términos de la velocidad\(c \) de fase de la ola. Pista: ¿Cuál es la distancia entre los frentes de onda a lo largo del\(x\) eje en comparación con la longitud de onda?
- Dos olas oceánicas de plano profundo con la misma frecuencia\(ω \) se mueven aproximadamente hacia el este. Sin embargo, una ola está orientada un pequeño ángulo\(β\) al norte del este y la otra está orientada al\(β \) sur de este.
- Determinar la orientación de las líneas de interferencia constructiva entre estas dos ondas.
- Determinar el espaciado entre líneas de interferencia constructiva.
- Un ejemplo de ondas con una relación de dispersión en la que la frecuencia es una función tanto de la magnitud como de la dirección del vector de onda se muestra gráficamente en la figura 2.21.
- ¿Cuál es la velocidad de fase de las ondas para cada uno de los tres vectores de onda? Pista: Es posible que desee obtener la longitud de cada vector de onda gráficamente.
- Para cada uno de los vectores de onda, ¿cuál es la orientación de los frentes de onda?
- Para cada uno de los vectores de onda ilustrados, dibuje otros dos vectores de onda cuyo valor promedio es aproximadamente el vector ilustrado, y cuyas puntas se encuentran en la misma línea de contorno de frecuencia. Determinar la orientación de las líneas de interferencia constructiva producidas por los pares superpuestos de ondas planas para las cuales cada uno de los pares vectoriales son los vectores de onda.
- Dos ondas gravitacionales tienen la misma frecuencia, pero longitudes de onda ligeramente diferentes.
- Si una onda tiene un ángulo de orientación\(θ \) =\(π∕\) 4 radianes, ¿cuál es el ángulo de orientación de la otra? (Véase la figura 2.6.)
- Determinar la orientación de las líneas de interferencia constructiva entre estas dos ondas.
- Una onda plana incide en una sola hendidura, extendiéndose un medio ángulo\(α \) después de la hendidura. Si todo el aparato está sumergido en un líquido con índice de refracción\(n \) = 1\(.\) 5, ¿cómo cambia el ángulo de dispersión de la luz? (Pista: Recordemos que el índice de refracción en un medio transparente es la relación entre la velocidad de la luz en el vacío y la velocidad en el medio. Además, cuando la luz pasa de un vacío a un medio transparente, la frecuencia de la luz no cambia. Por lo tanto, ¿cómo cambia la longitud de onda de la luz?)
Figura 2.21: Representación gráfica de la relación de dispersión para olas de aguas poco profundas en un río que fluye en la\(x \) dirección. Las unidades de frecuencia son hercios, las unidades de número de onda son metros inversos.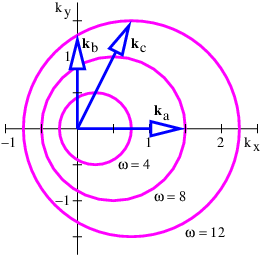
_____________________________________
- Determinar el diámetro del telescopio necesario para resolver un planeta 2 × 10 a 8 km de una estrella que está a 6 años luz de la tierra. (Supongamos luz azul que tiene una longitud de onda\(λ \) ≈ 4 × 10 - 7 m = 400 nm. Además, no te preocupes por la gran diferencia de brillo entre los dos a los efectos de este problema.)
- Un rayo láser de un láser en la tierra es rebotado a la tierra por un reflector de esquina en la luna.
- Los ingenieros encuentran que la señal devuelta es más fuerte si el rayo láser es inicialmente extendido por el expansor de haz que se muestra en la figura 2.22. Explique por qué esto es así.
- El haz tiene un diámetro de 1 m saliendo de la tierra. ¿Qué tan amplio es cuando llega a la luna, que está a 4 × 10 a 5 km de distancia? Supongamos que la longitud de onda de la luz es de 5 × 10 - 7 m.
- ¿Qué tan amplio sería el rayo láser en la luna si inicialmente no se pasara a través del expansor de haz? Supongamos que su diámetro inicial es de 1 cm.
- Supongamos que una onda plana incide en dos hendiduras en una barrera en un ángulo, de tal manera que la fase de la onda en una hendidura retarda la fase en la otra hendidura en media longitud de onda. ¿Cómo cambia el patrón de interferencia resultante del caso en el que no hay retraso?
- Supongamos que una pieza delgada de vidrio de índice de refracción\(n \) = 1\(.\) 33 se coloca frente a una hendidura de una configuración de difracción de dos hendiduras.
- ¿Qué tan grueso tiene que ser el vidrio para ralentizar la onda entrante para que quede rezagada la ola que pasa por la otra hendidura por una diferencia de fase de\(π\)? Tomar la longitud de onda de la luz para que sea\(λ \) = 6 × 10 - 7 m.
- Para la situación anterior, describa cualitativamente cómo cambia el patrón de difracción con respecto al caso en el que no hay vidrio frente a una de las hendiduras. Explica tus resultados.
Figura 2.22: Croquis de un expansor de haz para un láser.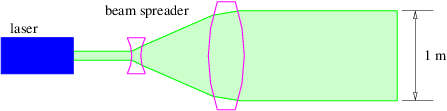
_____________________________________
- Una fuente de luz produce dos longitudes de onda,\(λ\) 1 = 400 nm (azul) y\(λ\) 2 = 600 nm (rojo).
- Esboce cualitativamente el patrón de difracción de dos rendijas de esta fuente. Esboce el patrón para cada longitud de onda por separado.
- Esboce cualitativamente el patrón de difracción de 16 hendiduras de esta fuente, donde el espaciado de las ranuras es el mismo que en el caso de las dos ranuras
- Una fuente de luz produce dos longitudes de onda,\(λ\) 1 = 631 nm y\(λ\) 2 = 635 nm. ¿Cuál es el número mínimo de hendiduras necesarias en un espectrómetro de rejilla para resolver las dos longitudes de onda? (Supongamos que está viendo el pico de difracción de primer orden.) Esboce el pico de difracción de cada longitud de onda e indique qué tan estrechos deben ser los picos para resolverlos.
Capítulo 3 Óptica Geométrica
Como se mostró anteriormente, cuando una onda plana incide sobre una abertura que tiene dimensiones mucho mayores que la longitud de onda de la onda, los efectos de difracción son mínimos y un segmento de la onda plana pasa a través de la abertura esencialmente inalterado. Este segmento de onda plana puede pensarse como un paquete de ondas, llamado haz o rayo, que consiste en una superposición de vectores de onda muy cercanos en dirección y magnitud al vector de onda central del paquete de ondas. En la mayoría de los casos el rayo simplemente se mueve en la dirección definida por el vector de onda central, es decir, normal a la orientación de los frentes de onda. Sin embargo, esto no es cierto cuando el medio a través del cual se propaga la luz es ópticamente anisotrópico, es decir, la luz que viaja en diferentes direcciones se mueve a diferentes velocidades de fase. Un ejemplo de tal medio es un cristal de calcita. En el caso anisotrópico, la orientación del rayo se puede determinar una vez que se conoce la relación de dispersión para las ondas en cuestión, utilizando las técnicas desarrolladas en el capítulo anterior.
Si la luz se mueve a través de algún aparato en el que todas las aberturas son mucho mayores en dimensión que la longitud de onda de la luz, entonces podemos usar la regla anterior para seguir los rayos de luz a través del aparato. A esto se le llama aproximación óptica geométrica.
Reflexión y refracción
La mayor parte de lo que necesitamos saber sobre la óptica geométrica se puede resumir en dos reglas, las leyes de la reflexión y la refracción. Estas reglas pueden inferirse considerando lo que sucede cuando un segmento de onda plana incide sobre una superficie plana. Si la superficie es de metal pulido, la onda se refleja, mientras que si la superficie es una interfaz entre dos medios transparentes con diferentes índices de refracción, la onda se refleja parcialmente y se refracta parcialmente. Reflexión significa que la onda se vuelve a convertir en el medio espacio del que proviene, mientras que la refracción significa que pasa a través de la interfaz, adquiriendo una dirección de movimiento diferente a la que tenía antes de llegar a la interfaz.
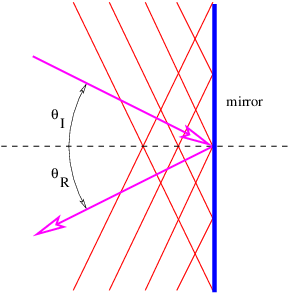
La Figura 3.1 muestra el vector de onda y el frente de onda de una onda que se refleja desde un espejo plano. Los ángulos de incidencia,\(θ\) I, y reflexión,\(θ\) R, se definen como los ángulos entre los vectores de onda entrante y saliente respectivamente y la línea normal al espejo. La ley de la reflexión establece que\(θ\) R =\(θ\) I. Esto es consecuencia de la necesidad de que los frentes de onda entrante y saliente estén en fase entre sí a lo largo de la superficie del espejo. Esto más la igualdad de las longitudes de onda entrantes y salientes es suficiente para asegurar el resultado anterior.
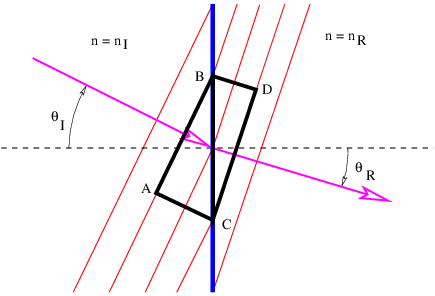
La refracción, como se ilustra en la figura 3.2, es un poco más complicada. Desde\(n\) R\(> n\) I, la velocidad de la luz en el medio derecho es menor que en el medio izquierdo. (Recordemos que la velocidad de la luz en un medio con índice de refracción\(n \) es\(c\) media =\(c\) vac\(∕n\).) La frecuencia del paquete de ondas no cambia a medida que pasa a través de la interfaz, por lo que la longitud de onda de la luz en el lado derecho es menor que la longitud de onda en el lado izquierdo.
Examinemos el triángulo ABC en la figura 3.2. El lado AC es igual al lado BC veces pecado (\(θ\)I). Sin embargo, la CA también es igual a 2\(λ\) I, o el doble de la longitud de onda de la onda a la izquierda de la interfaz. Razonamiento similar muestra que 2\(λ\) R, dos veces la longitud de onda a la derecha de la interfaz, es igual a BC por pecado (\(θ\)R). Dado que el intervalo BC es común a los triángulos ABC y DBC, vemos fácilmente que
\[λI- = -sin(θI). λR sin(θR) \label{3.1}\]
Ya que\(λ\) I =\(c\) I\(T \) =\(c\) vac\(T∕n\) I y\(λ\) R =\(c\) R\(T \) = \(c\)vac\(T∕n\) R donde\(c\) I y\(c\) R son las velocidades de onda a la izquierda y derecha de la interfaz,\(c\) vac es la velocidad de luz en un vacío, y\(T \) es el período (común), podemos refundir fácilmente la ecuación anterior en la forma
\[nI sin(θI) = nR sin (θR ). \label{3.2}\]
A esto se le llama ley de Snell, y gobierna cómo se dobla un rayo de luz a medida que pasa por una discontinuidad en el índice de refracción. El ángulo\(θ\) I se llama ángulo incidente y\(θ\) R se llama ángulo refractado. Observe que estos ángulos se miden desde la normal hasta la superficie, no la tangente.
Reflexión interna total
Cuando la luz pasa de un medio de menor índice de refracción a uno con mayor índice de refracción, la ley de Snell indica que el rayo se dobla hacia la normal a la interfaz. El revés ocurre cuando el paso está en la otra dirección. En esta última circunstancia surge una situación especial cuando la ley de Snell predice un valor para el seno del ángulo refractado mayor que uno. Esto es físicamente insostenible. Lo que realmente sucede es que la onda incidente se refleja desde la interfaz. A este fenómeno se le llama reflexión interna total. El ángulo de incidencia mínimo para el que se produce la reflexión interna total se obtiene sustituyendo\(θ\) R =\(π∕\) 2 en la ecuación 3.2}, dando como resultado
\[sin (θI) = nR ∕nI (total internal reflection). \label{3.3}\]
Medios Anisotrópicos
Observe que la ley de Snell hace la suposición implícita de que los rayos de luz se mueven en la dirección del vector de onda de la luz, es decir, normal a los frentes de onda. Como deja claro el análisis del capítulo anterior, esto sólo es válido cuando el medio óptico es isotrópico, es decir, la frecuencia de onda depende únicamente de la magnitud del vector de onda, no de su dirección.
Ciertos tipos de cristales, como los hechos de calcita, no son isotrópicos: la velocidad de la luz en dichos cristales, y de ahí la frecuencia de onda, depende de la orientación del vector de onda. Como ejemplo, la frecuencia angular en un medio anisotrópico podría tomar la forma
\[ [c2(kx + ky)2 c2(kx - ky)2]1∕2 ω = -1----------+ -2---------- , 2 2 \label{3.4} \]
donde\(c\) 1 es la velocidad de la luz para las ondas en la que\(k\) y =\(k\) x, y\(c\) 2 es su velocidad cuando\(k\) y = - \(k\)x.
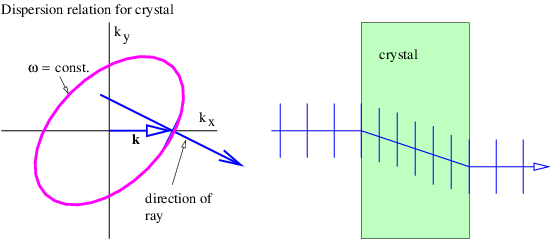
La Figura 3.3 muestra un ejemplo en el que un rayo golpea un cristal de calcita orientado de manera que los contornos de frecuencia constante son como se especifica en la ecuación 3.4}. El vector de onda está orientado normal a la superficie del cristal, de manera que los frentes de onda son paralelos a esta superficie. Al ingresar al cristal, la orientación del frente de onda debe permanecer igual para preservar la continuidad de fase en la superficie. Sin embargo, debido a la anisotropía de la relación de dispersión de la luz en el cristal, la dirección del rayo cambia como se muestra en el panel derecho. ¡Este comportamiento es claramente inconsistente con la versión habitual de la ley de Snell!
Es posible extender la ley de Snell al caso anisotrópico. Sin embargo, aquí no vamos a presentar esto. Las siguientes discusiones sobre los instrumentos ópticos siempre supondrán que se utilizan medios ópticos isotrópicos.
Ecuación de lentes e instrumentos ópticos
Dadas las leyes de reflexión y refracción, se puede ver en principio cómo se podía rastrear el paso de la luz a través de un instrumento óptico. Para cada uno de un número de rayos iniciales, se puede calcular el cambio en la dirección del rayo en cada superficie especular o interfaz de índice de refracción. Entre estos puntos, el rayo traza una línea recta.
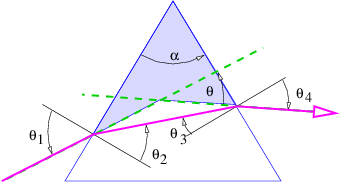
Aunque de concepción simple, este procedimiento puede ser bastante complejo en la práctica. Sin embargo, el procedimiento simplifica si una serie de aproximaciones, llamadas colectivamente aproximación de lente delgada, son válidas. Comenzamos con el cálculo de la flexión de un rayo de luz a medida que pasa por un prisma, como se ilustra en la figura 3.4.
Las piezas de información necesarias para encontrar\(θ\), el ángulo a través del cual se desvía el rayo, son las siguientes: la geometría del triángulo definida por los puntos de entrada y salida del rayo y el vértice superior del prisma conduce a
\[α + (π∕2 - θ ) + (π∕2 - θ ) = π, 2 3 \label{3.5}\]
lo que simplifica
\[α = θ2 + θ3. \label{3.6}\]
La ley de Snell en los puntos de entrada y salida del rayo nos dicen que
\[ sin-(θ1) sin-(θ4) n = sin (θ ) n = sin (θ ), 2 3 \label{3.7} \]
donde\(n \) está el índice de refracción del prisma. (Se supone que el índice de refracción del entorno es la unidad.) También se puede inferir que
\[θ = θ1 + θ4 - α. \label{3.8}\]
Esto viene del hecho de que la suma de los ángulos internos del cuadrilátero sombreado en la figura 3.4 es
\[(π ∕2 - θ1) + α + (π ∕2 - θ4) + (π + θ) = 2π. \label{3.9}\]
Combinar las ecuaciones (3.6), (3.7) y (3.8) permite determinar la deflexión\(θ \) del rayo en términos de\(θ\) 1 y\(α\), pero la expresión resultante es muy desordenada. Sin embargo, se produce una gran simplificación si se cumplen las siguientes condiciones:
- El\(α \) ángulo 1.
- Los ángulos\(θ\) 1\(,\)\( θ\) 2\(,\)\( θ\) 3\(,\)\( θ\) 4 1.
Con estas aproximaciones es fácil demostrar que
\[θ = α(n - 1) (small angles). \label{3.10}\]
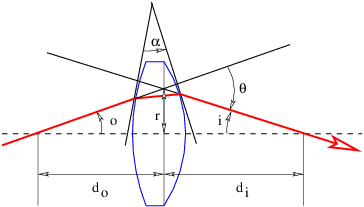
En términos generales, las lentes y espejos en los instrumentos ópticos tienen superficies curvas en lugar de planas. Sin embargo, todavía podemos usar las leyes para la reflexión y refracción por superficies planas siempre y cuando el segmento de la superficie sobre la que incide el paquete de ondas no esté muy curvado en la escala de las dimensiones del paquete de ondas. Esta condición es fácil de satisfacer con la luz que incide en los instrumentos ópticos ordinarios. En este caso, la deflexión de un rayo de luz viene dada por la ecuación 3.10} si\(α \) se define como la intersección de las líneas tangentes a los puntos de entrada y salida del rayo, como se ilustra en la figura 3.5.
Una lente positiva es más gruesa en el centro que en los bordes. El ángulo\(α \) entre las líneas tangentes a las dos superficies de la lente a una\(r \) distancia del eje central toma la forma\(α \) =\(Cr\), donde\(C \) es una constante. El ángulo de deflexión de un haz que golpea la lente a una\(r \) distancia del centro es, por lo tanto,\(θ \) =\(Cr\) (\(n \)- 1), como se indica en la figura 3.5. Los ángulos\(o \) y la\(i \) suma al ángulo de deflexión:\(o \) +\(i \)\(θ \) = =\(Cr\) (\(n \)- 1). Sin embargo, en la medida en que se mantiene la aproximación de ángulo pequeño,\(o \)\(i \) =\(r∕d\) o y =\(r∕d\) i donde\(d\) o es la distancia al objeto e\(d\) i es la distancia a la imagen del objeto. Armando estas ecuaciones y cancelando los\(r \) resultados en la ecuación de lente delgada:
\[1-- 1- 1- d + d = C (n - 1) ≡ f . o i \label{3.11} \]
La cantidad\(f \) se llama distancia focal de la lente. Observe que\(f \) =\(d\) i si el objeto está muy lejos de la lente, i. e., si\(d\) o es extremadamente grande.
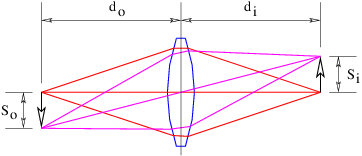
La Figura 3.6 muestra cómo una lente positiva hace una imagen. La imagen es producida por toda la luz de cada punto del objeto que cae sobre un punto correspondiente de la imagen. Si la flecha de la izquierda es un objeto iluminado, aparecerá una imagen de la flecha a la derecha si se permite que la luz que viene de la lente caiga sobre una hoja de papel o una pantalla de vidrio esmerilado. El tamaño del objeto\(S\) o y el tamaño de la imagen\(S\) i están relacionados por geometría simple con las distancias del objeto y la imagen desde la lente:
\[Si-= di. So do \label{3.12}\]
Observe que una lente positiva invierte la imagen.
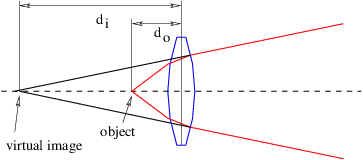
Se producirá una imagen a la derecha de la lente solo si\(d\) o\(> f\). Si\(d\) o\(< f\), la lente es incapaz de converger los rayos de la imagen a un punto, como se ve en la figura 3.7. Sin embargo, en este caso la extensión hacia atrás de los rayos converge en un punto llamado imagen virtual, que en el caso de una lente positiva siempre está más lejos de la lente que del objeto. La imagen se llama virtual porque no aparece en una pantalla de vidrio esmerilado colocada en este punto. A diferencia de la imagen real que se ve en la figura 3.6, la imagen virtual no se invierte. La ecuación de lente delgada todavía se aplica si la distancia desde la lente a la imagen se toma para ser negativa.
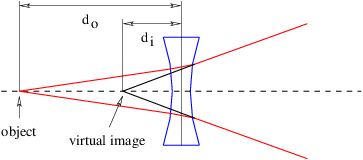
Una lente negativa es más delgada en el centro que en los bordes y produce solo imágenes virtuales. Como se ve en la figura 3.8, la imagen virtual producida por una lente negativa está más cerca de la lente que el objeto. Nuevamente, la ecuación de lente delgada sigue siendo válida, pero tanto la distancia de la imagen a la lente como la distancia focal deben tomarse como negativas. Sólo la distancia al objeto permanece positiva.
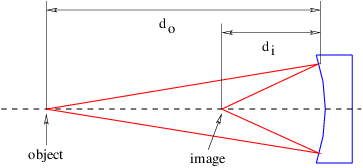
Los espejos curvos también producen imágenes de manera similar a una lente, como se muestra en la figura 3.9. Un espejo cóncavo, como se ve en esta figura, trabaja en analogía con una lente positiva, produciendo una imagen real o virtual dependiendo de si el objeto está más alejado o más cerca del espejo que la distancia focal del espejo. Un espejo convexo actúa como una lente negativa, produciendo siempre una imagen virtual. La ecuación de lente delgada funciona en ambos casos siempre y cuando los ángulos sean pequeños.
Principio de Fermat
Un enfoque alternativo a la óptica geométrica se puede desarrollar desde el principio de Fermat. Este principio establece (en su forma más simple) que las ondas de luz de una frecuencia dada atraviesan la trayectoria entre dos puntos que toma el menor tiempo. El ejemplo más obvio de ello es el paso de la luz a través de un medio homogéneo en el que la velocidad de la luz no cambia con la posición. En este caso el menor tiempo corresponde a la distancia más corta entre los puntos, que, como todos sabemos, es una línea recta. Así, el principio de Fermat es consistente con la luz que viaja en línea recta en un medio homogéneo.
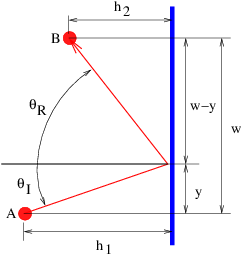
El principio de Fermat también puede ser utilizado para derivar las leyes de reflexión y refracción. Por ejemplo, la figura 3.10 muestra un rayo candidato a reflexión en el que los ángulos de incidencia y reflexión no son iguales. El tiempo requerido para que la luz pase del punto A al punto B es
\[t = ([h2 + y2]1∕2 + [h2+ (w - y)2]1∕2)∕c 1 2 \label{3.13}\]
donde\(c \) esta la velocidad de la luz. Encontramos el tiempo mínimo diferenciando\(t \) con respecto\(y \) y estableciendo el resultado a cero, con el resultado que
\[-----y----- = ------w---y------ . [h21 + y2]1∕2 [h22 + (w - y)2]1∕2 \label{3.14}\]
Sin embargo, observamos que el lado izquierdo de esta ecuación es simplemente pecado\(θ\) I, mientras que el lado derecho es pecado\(θ\) R, de manera que la condición de tiempo mínimo se reduce a pecado\(θ\) I = pecado\(θ\) R o\(θ\) I =\(θ\) R, que es la ley de la reflexión.
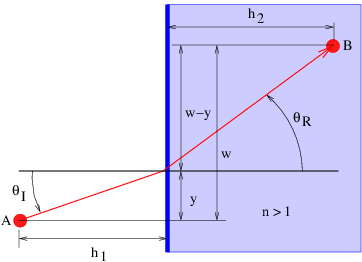
Se puede hacer un análisis similar para derivar la ley de refracción de Snell. La velocidad de la luz en un medio con índice de refracción\(n \) es\(c∕n\), donde\(c \) está su velocidad en un vacío. Así, el tiempo requerido para que la luz vaya a cierta distancia en tal medio es el\(n \) tiempo que tarda la luz en recorrer la misma distancia en un vacío. Refiriéndose a la figura 3.11, el tiempo requerido para que la luz pase de A a B se convierte en
\[ 2 2 1∕2 2 2 1∕2 t = ([h 1 + y ] + n [h2 + (w - y )] )∕c. \label{3.15}\]
Esto da como resultado la condición
\[sin θI = nsinθR \label{3.16}\]
donde\(θ\) R es ahora el ángulo refractado. Reconocemos este resultado como la ley de Snell.
Observe que el caso de reflexión ilustra un punto sobre el principio de Fermat: El tiempo mínimo puede ser en realidad un mínimo local más que global — después de todo, en la figura 3.10, ¡la distancia mínima global de A a B sigue siendo solo una línea recta entre los dos puntos! De hecho, la luz a partir del punto A llegará al punto B por ambas rutas —la ruta directa y la ruta reflejada.
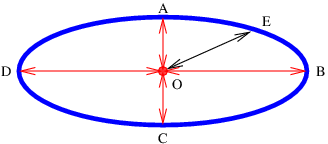
Resulta que las trayectorias permitidas por el principio de Fermat no tienen que ser estrictamente trayectorias de tiempo mínimo. También pueden ser trayectorias de tiempo máximo, como se ilustra en la figura 3.12. En este caso, la luz emitida en el punto O puede reflejarse de vuelta al punto O desde cuatro puntos en el espejo, A, B, C y D. Las trayectorias O-A-O y O-C-O son trayectorias de tiempo mínimo mientras que O-B-O y O-D-O son trayectorias de tiempo máximo.
El principio de Fermat parece bastante misterioso. No obstante, el físico estadounidense Richard Feynman le dio sentido al invocar un principio aún más fundamental, como vemos ahora.
Si un rayo de luz se origina en el punto O de la figura 3.12, se refleja en la superficie elipsoidal del espejo en el punto A, y vuelve al punto O, el tiempo transcurrido no es muy diferente del que experimenta un rayo que se refleja en el espejo a una ligera distancia del punto A y vuelve a O. Esto se debe a que en el punto A el haz desde el punto O es perpendicular a la tangente a la superficie del espejo en el punto A. En contraste, el tiempo experimentado por un rayo que va del punto O al punto E y hacia atrás diferiría en una cantidad mucho mayor que el tiempo experimentado por un rayo reflejando en el espejo una ligera distancia del punto E. Esto es porque la tangente a la superficie del espejo en el punto E no es perpendicular a la viga desde el punto O.
Técnicamente, el cambio en el tiempo de ida y vuelta varía linealmente con la desviación en el punto de reflexión desde el punto E, pero cuadráticamente con la desviación del punto A. Si esta desviación es pequeña en primer lugar, entonces el cambio en el tiempo de ida y vuelta será mucho menor para el caso cuadrático que para el caso lineal.
Parece extraño que habláramos de un haz reflejando de nuevo al punto O si choca contra el espejo en cualquier punto excepto A, B, C o D, debido a los requisitos de la ley de reflexión. No obstante, recordemos que la propia ley de reflexión depende del principio de Fermat, por lo que no podemos asumir la validez de esa ley en esta investigación.
Feynman postuló que los rayos de luz exploran todos los caminos posibles de un punto a otro, pero que los únicos caminos realizados en la naturaleza son aquellos para los cuales la luz que toma caminos cercanos experimenta casi el mismo tiempo transcurrido (o más generalmente, atraviesa casi el mismo número de longitudes de onda ) como el camino original. Si esto es cierto, entonces los rayos vecinos interfieren constructivamente entre sí, resultando en un haz mucho más brillante de lo que ocurriría en ausencia de esta interferencia constructiva. Así, las rutas de ida y vuelta O-A-O, O-B-O, O-C-O y O-D-O en la figura 3.12 ocurren realmente, pero no O-E-O. ¡Feynman explica el principio de Fermat invocando interferencias constructivas y destructivas!
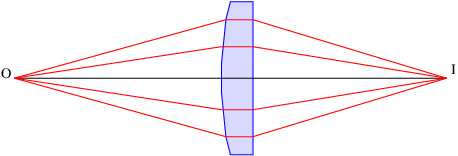
La figura 3.13 ilustra una situación bastante peculiar. Observe que todos los rayos del punto O que interceptan la lente terminan en el punto I. Esto parecería contradecir el principio de Fermat, en que solo deberían ocurrir las trayectorias de tiempo mínimo (o máximo). Sin embargo, un cálculo muestra que todas las trayectorias ilustradas en este caso particular toman el mismo tiempo. Así, la luz no puede elegir una trayectoria sobre otra usando el principio de Fermat y todas las trayectorias son igualmente favorecidas. Tenga en cuenta que esta inferencia se aplica no a cualquier conjunto de trayectorias, sino solo a aquellas que van desde un punto de objeto hasta el punto de imagen correspondiente.
Problemas
- El índice de refracción varía como se muestra en la figura 3.14:
- Dado\(θ\) 1, usa la ley de Snell para encontrar\(θ\) 2.
- Dado\(θ\) 2, usa la ley de Snell para encontrar\(θ\) 3.
- De los resultados anteriores, encontrar\(θ\) 3, dado\(θ\) 1. ¿Importa\(n\) \(θ\)2 o 2?
Figura 3.14: Refracción a través de múltiples capas paralelas con diferentes índices de refracción.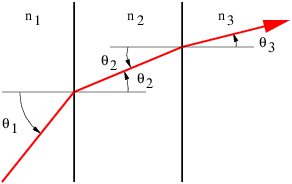
_____________________________________
- Se utiliza un prisma de 45 ° -45 ° -90° para reflejar totalmente la luz a través de 90 ° como se muestra en la figura 3.15. ¿Cuál es el índice mínimo de refracción del prisma necesario para que esto funcione?
Figura 3.15: Refracción a través de un prisma de 45 ° -45° -90°.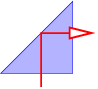
_____________________________________
- Mostrar gráficamente en qué dirección debe apuntar el vector de onda dentro del cristal de calcita de la figura 3.3 para que un rayo de luz esté orientado horizontalmente. Esbozar la orientación de los frentes de onda en este caso.
Figura 3.16: Enfoque de rayos paralelos mediante un espejo parabólico.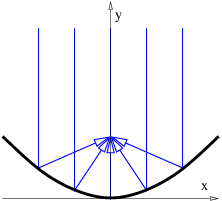
_____________________________________
Figura 3.17: Refracción a través de un prisma en forma de cuña.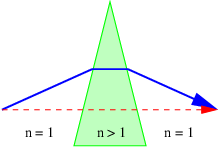
_____________________________________
- El ojo humano es una lente que enfoca imágenes en una pantalla llamada retina. Supongamos que la distancia focal normal de esta lente es de 4 cm y que ésta enfoca imágenes de objetos lejanos en la retina. Supongamos que el ojo es capaz de enfocarse en objetos cercanos cambiando la forma de la lente, y por lo tanto su distancia focal. (La distancia entre lentes y retina sigue siendo la misma). Si un objeto está a 20 cm del ojo, ¿cuál debe ser la distancia focal alterada del ojo para que la imagen de este objeto esté enfocada en la retina?
- Una ameba de 0\(.\) 01 cm de diámetro tiene su imagen proyectada sobre una pantalla como se muestra en la figura 3.18 mediante una lente positiva de diámetro 0\(.\) 1 cm.
- ¿Qué tan grande es la imagen de la ameba?
- ¿Cuál es la distancia focal de la lente?
- ¿Cuál es la distancia mínima entre entidades en la imagen de la ameba que se puede resolver? Supongamos que la longitud de onda de la luz utilizada es de 5 × 10 - 7 m. (Pista: ¿Cuál es el ángulo de dispersión de un haz de luz que pasa por una abertura del tamaño de la lente?)
Figura 3.18: Una ameba fotografiada por una lente.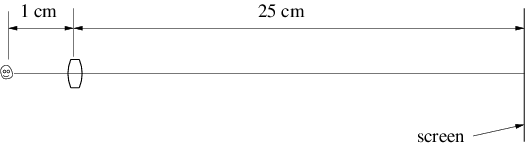
_____________________________________
- El gran telescopio refractor del Observatorio Yerkes en Wisconsin (ver figura 3.19) tiene lente primaria\(D \) = 1\(.\) 02 m de diámetro con una distancia focal de\(L \) = 19\(.\) 4 m. Usa la aproximación de ángulo pequeño en todos los cálculos y asume que la luz tiene longitud de onda 5 × 10 - 7 m.
- Júpiter tiene un diámetro de 1\(.\) 5 × 10 5 km y una distancia promedio de la tierra de 8 × 10 8 km. ¿Qué tan grande es la imagen de Júpiter (en cm) en el plano focal de la lente primaria?
- Dadas las perfectas condiciones atmosféricas de “visión”, ¿a qué distancia deben estar dos características en Júpiter (en km) para que el telescopio Yerkes pueda resolverlas?
- ¿Cuál debería ser la distancia focal\(l \) del cristalino secundario o del ocular para que Júpiter subtienda el mismo ángulo que la luna subtiende a simple vista? El diámetro de la luna es de 3\(.\) 5 × 10 3 km y su distancia de la tierra es de 3\(.\) 8 × 10 5 km. Sugerencia: Imagínese que se coloca una lámina translúcida de vidrio esmerilado en el plano focal para que la imagen se vea proyectada sobre este vidrio esmerilado, que dispersa la luz en un amplio rango de ángulos. El ocular puede entonces pensarse como una lupa con la que se puede examinar la imagen en el cristal esmerilado. Usando este arteface, es necesario considerar solo los rayos de luz que pasan por el centro de cada lente.
Figura 3.19: El gran telescopio refractor Yerkes observando a Júpiter.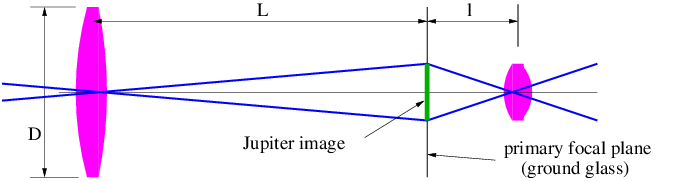
_____________________________________
- Mostrar que un espejo cóncavo que enfoca los rayos entrantes paralelos al eje óptico del espejo a un punto en el eje óptico, como se ilustra en la figura 3.16, es de forma parabólica. Sugerencia: Dado que los rayos que siguen diferentes caminos se mueven desde la fuente distante hasta el punto focal del espejo, el principio de Fermat implica que todos estos rayos tardan el mismo tiempo en hacerlo (¿por qué es esto?) , y por lo tanto todos recorren la misma distancia.
- Utilice el principio de Fermat para explicar cualitativamente por qué un rayo de luz sigue la línea sólida en lugar de la línea discontinua a través de la cuña de vidrio que se muestra en la figura 3.17.
- Pon a prueba tu conocimiento del principio de Fermat usando la ecuación 3.15} para derivar la ley de Snell.
- }
Capítulo 4 Relatividad Especial
Albert Einstein inventó las teorías especiales y generales de la relatividad a principios del siglo XX, aunque muchas otras personas contribuyeron al clima intelectual que hizo posible estos descubrimientos. La teoría especial de la relatividad surgió de un conflicto entre las ideas de la mecánica desarrolladas por Galileo y Newton, y la teoría del electromagnetismo. Por esta razón, la relatividad se suele discutir en los libros de texto después de que se desarrolla el electromagnetismo. Sin embargo, la relatividad especial es en realidad una extensión válida de la cosmovisión galilea que se necesita cuando los objetos se mueven a velocidades muy altas, y solo se relaciona casualmente con el electromagnetismo. Por esta razón discutimos la relatividad antes del electromagnetismo.
El único hecho del electromagnetismo que necesitamos se introduce ahora: Hay una velocidad máxima a la que los objetos pueden viajar. Esto es coincidentemente igual a la velocidad de la luz en un vacío,\(c \) = 3 × 10 8 m s - 1. Además, una medición de la velocidad de un haz de luz en particular produce la misma respuesta independientemente de la velocidad de la fuente de luz o la velocidad a la que se mueve el instrumento de medición.
Este resultado experimental bastante extraño contrasta con lo que ocurre en la relatividad galilea. Si dos autos pasan por un peatón parado en una acera, uno a 20 m s - 1 y el otro a 50 m s - 1, el auto más rápido parece estar moviéndose a 30 m s - 1 en relación con el auto más lento. Sin embargo, si un haz de luz que se mueve a 3 × 10 8 m s - 1 pasa una nave espacial interestelar que se mueve a 2 × 10 8 m s - 1, entonces aparece el haz de luz a ocupantes de la nave espacial para estar moviéndose a 3 × 10 8 m s - 1, no 1 × 10 8 m s - 1. Además, si la nave espacial emite una señal luminosa hacia su planeta de destino (estacionario), entonces el haz resultante parece estar moviéndose a 3 × 10 8 m s - 1 a los instrumentos en el destino, no a 5 × 10 8 m s - 1.
El hecho de que estemos hablando de haces de luz es sólo por conveniencia. Cualquier otro medio de enviar una señal a la velocidad máxima permitida resultaría en el mismo comportamiento. Por lo tanto, no podemos buscar la respuesta a esta aparente paradoja en las propiedades especiales de la luz. En cambio tenemos que mirar a la naturaleza básica del espacio y el tiempo.
Pensamiento Galileo del Espacio-Tiempo
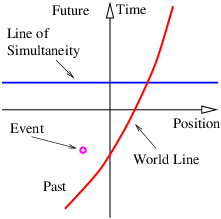
Para comprender tanto la relatividad galileana como la einsteiniana es importante comenzar a pensar en el espacio y el tiempo como dimensiones diferentes de un espacio cuatridimensional llamado espacio-tiempo. En realidad, como no podemos visualizar muy bien cuatro dimensiones, es más fácil comenzar con una sola dimensión espacial y la dimensión de tiempo. La Figura 4.1 muestra una gráfica con el tiempo trazada en el eje vertical y la dimensión de un espacio trazada en el eje horizontal. Un evento es algo que ocurre en un momento determinado y en un punto particular del espacio. (“Julius X. destroza su automóvil en Lempitar, NM el 21 de junio a las 6:17 PM.”) Una línea de mundo es una gráfica de la posición de algún objeto en función del tiempo en un diagrama de espacio-tiempo, aunque es convencional poner el tiempo en el eje vertical. Así, una línea mundial es realmente una línea en el espacio-tiempo, mientras que un evento es un punto en el espacio-tiempo. Una línea horizontal paralela al eje de posición es una línea de simultaneidad en la relatividad galilea, es decir, todos los eventos en esta línea ocurren simultáneamente.
En un diagrama de espacio-tiempo la pendiente de una línea mundial tiene un significado especial. Observe que una línea vertical del mundo significa que el objeto que representa no se mueve — la velocidad es cero. Si el objeto se mueve hacia la derecha, entonces la línea mundial se inclina hacia la derecha, y cuanto más rápido se mueve, más se inclina la línea mundial. Cuantitativamente, decimos que
\[ ---------1-------- velocity = slope of world line \label{4.1}\]
en la relatividad galilea. Observe que esto funciona para pendientes y velocidades negativas así como positivas. Si el objeto cambia su velocidad con el tiempo, entonces la línea del mundo se curva, y la velocidad instantánea en cualquier momento es la inversa de la pendiente de la tangente a la línea del mundo en ese momento.
Lo más difícil de darse cuenta de los diagramas espacio-tiempo es que representan el pasado, el presente y el futuro, todo en un diagrama. Así, los diagramas de espacio-tiempo no cambian con el tiempo; la evolución de los sistemas físicos se representa observando los sucesivos cortes horizontales en el diagrama en tiempos sucesivos. Los diagramas espacio-tiempo representan la evolución, pero no evolucionan ellos mismos.
El principio de relatividad establece que las leyes de la física son las mismas en todos los marcos de referencia inerciales. Un marco de referencia inercial es aquel que no se acelera. Los marcos de referencia unidos a un automóvil en reposo y a un automóvil que se mueve constantemente por la autopista a 30 m s - 1 son ambos inerciales. Un marco de referencia unido a un automóvil que acelera lejos de un semáforo no es inercial.
El principio de relatividad es una suposición o hipótesis educada basada en una amplia experiencia. Si el principio de relatividad no fuera cierto, tendríamos que hacer todos nuestros cálculos en algún marco de referencia preferido. Esto sería muy molesto. Sin embargo, el problema más fundamental es que no tenemos idea de cuál podría ser la velocidad de este cuadro preferido. ¿Se mueve con la tierra? Eso estaría muy centrado en la tierra. ¿Qué tal la velocidad del centro de nuestra galaxia o la velocidad media de todas las galaxias? En lugar de enfrentar el tema de un marco de referencia preferido, los físicos han optado por atenerse al principio de la relatividad.

Si un objeto se mueve hacia la izquierda a una velocidad\(v \) relativa a un marco de referencia particular, parece estar moviéndose a una velocidad\(v\) ′ =\(v \) -\(U \) relativa a otro marco de referencia que a su vez se mueve a velocidad\(U\). Esta es la ley de transformación de la velocidad galilea, y se basa en la experiencia cotidiana. Si estás viajando 30 m s - 1 por la autopista y otro carro te pasa haciendo 40 m s - 1, entonces el otro carro pasa a tu lado a 10 m s - 1 relativo a tu auto.
La Figura 4.2 muestra cómo la línea mundial de un objeto se representa de manera diferente en los marcos de referencia no cebado (\(x\),\(t\)) y cebado (\(x\)\(t\)′, ′). La diferencia entre la velocidad del objeto y la velocidad del marco cebado (es decir, la diferencia en las inversas de las pendientes de las líneas mundiales correspondientes) es la misma en ambos marcos de referencia en este caso galileo. Esto ilustra la diferencia entre una ley física independiente del marco de referencia (la diferencia entre las velocidades en la relatividad galilea) y el movimiento diferente del objeto en los dos marcos de referencia diferentes.
Pensamiento del espacio-tiempo en la relatividad especial
En la relatividad especial encontramos que el espacio y el tiempo “se mezclan” de una manera que no lo hacen en la relatividad galilea. Esto sugiere que el espacio y el tiempo son aspectos diferentes de una misma “cosa”, a la que llamamos espacio-tiempo.
Si el tiempo y la posición son simplemente dimensiones diferentes del mismo espacio abstracto, entonces deberían tener las mismas unidades. La forma más fácil de organizar esto es multiplicar el tiempo por la velocidad máxima\(c\), lo que resulta en el tipo de diagrama espacio-tiempo que se muestra en la figura 4.3. Observe que las líneas mundiales de luz tienen pendiente ± 1 cuando el eje de tiempo se escala de esta manera. Además, la relación entre la velocidad y la pendiente de una línea mundial debe revisarse para que se lea
\[ ---c-- v = slope (world line). \label{4.2}\]
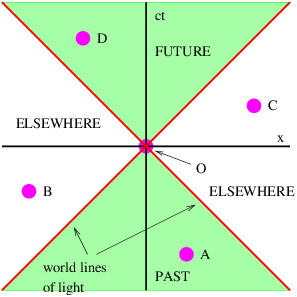
Observe que es físicamente posible que un objeto tenga una línea mundial que conecte el evento O en el origen y los eventos A y D en la figura 4.3, ya que la pendiente de la línea mundial resultante superaría la unidad, y así representaría una velocidad menor que la velocidad de la luz. Los eventos que pueden estar conectados por una línea mundial se llaman como temporales relativos entre sí. Por otro lado, el evento O no puede estar conectado a los eventos B y C por una línea mundial, ya que esto implicaría una velocidad mayor que la velocidad de la luz. Los eventos que no pueden ser conectados por una línea mundial se llaman espaciosos entre sí. Observe la terminología en la figura 4.3: El evento A está en el pasado del evento O, mientras que el evento D está en el futuro. Los eventos B y C están en otros lugares relativos al evento O.
Postulados de la Relatividad Especial
Como aprendimos anteriormente, el principio de relatividad establece que las leyes de la física son las mismas en todos los marcos de referencia inerciales. El principio de relatividad se aplica a la relatividad einsteiniana tal como se aplica a la relatividad galilea.
Observe que la constancia de la velocidad de la luz en todos los marcos de referencia es consistente con el principio de relatividad. Sin embargo, como se señaló anteriormente, es inconsistente con nuestras nociones de cómo se suman las velocidades, o alternativamente, cómo pensamos que debería verse el mundo a partir de los marcos de referencia que se mueven a diferentes velocidades. Hemos llamado a la forma clásica de entender la visión desde diferentes marcos de referencia relatividad galilea. La nueva forma que reconcilia el comportamiento de los objetos que se mueven a velocidades muy altas se llama relatividad einsteiniana. La gran contribución de Einstein fue descubrir las leyes que nos dicen cómo se ve el mundo a partir de marcos de referencia que se mueven a altas velocidades entre sí. Estas leyes constituyen una geometría del espacio-tiempo, y de ellas se pueden derivar todas las de relatividad especial.
Todos los hechos observados sobre el espacio-tiempo pueden derivarse de dos postulados:
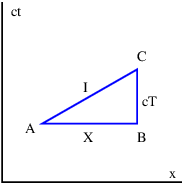
- Si dos eventos son simultáneos depende del marco de referencia desde el que se visualizan.
- El espacio-tiempo obedece a un teorema de Pitágoras modificado, que da la distancia\(I\), en espacio-tiempo o intervalo espacio-tiempo como
- \[ 2 2 2 2 I = X - c T , \label{4.3}\]
donde\(X\),\(T\), y\(I \) se definen en la figura 4.4.
Discutamos estos postulados a su vez.
simultaneidad
La forma clásica de pensar sobre la simultaneidad está tan arraigada en nuestros hábitos cotidianos que tenemos muchas dificultades para ajustarnos a lo que la relatividad especial tiene que decir sobre este tema. En efecto, entender cómo la relatividad cambia este concepto es la parte más difícil de la teoría; una vez que entiendes esto, ¡estás en camino de dominar la relatividad!
Antes de abordar la simultaneidad, pensemos primero en la colocación. Dos eventos (como A y E en la figura 4.5) son colocados si tienen el mismo\(x \) valor. Sin embargo, la colocación es un concepto que depende del marco de referencia. Por ejemplo, George está conduciendo de Boston a Washington, siendo la línea que pasa por los eventos A y D su línea mundial. Justo cuando pasa por Nueva York estornuda (evento A en la figura 4.5). Mientras conduce por Baltimore, vuelve a estornudar (evento D). En el marco de referencia de la tierra, estos dos estornudos no están colocados, ya que están separados por muchos kilómetros. No obstante, en el marco de referencia del auto de George, ocurren en el mismo lugar — ¡asumiendo que George no ha dejado el asiento del conductor!
Observe que dos eventos cualesquiera separados por un intervalo similar al tiempo se ubican en algún marco de referencia. La velocidad del marco de referencia viene dada por la ecuación 4.2}, donde la pendiente es simplemente la pendiente de la línea mundial que conecta los dos eventos.
En la relatividad galilea, si dos eventos son simultáneos, los consideramos simultáneos en todos los marcos de referencia. Por ejemplo, si dos relojes, uno en Nueva York y otro en Los Ángeles, golpean la hora al mismo tiempo en el marco de referencia terrestre, entonces en la relatividad galilea estos eventos también parecen ser simultáneos a los instrumentos del transbordador espacial mientras vuela sobre Estados Unidos. Sin embargo, si el transbordador espacial se mueve de oeste a este, es decir, de Los Ángeles hacia Nueva York, ¡mediciones cuidadosas demostrarán que el reloj en Nueva York marca la hora antes del reloj en Los Ángeles! Por lo tanto, el punto de vista galileo no es exacto.
Así como la colocación depende del marco de referencia de uno, este resultado muestra que la simultaneidad también depende del marco de referencia. La Figura 4.5 muestra cómo funciona esto. En la figura 4.5 los eventos A y B son simultáneos en el resto o marco de referencia no cebado. Sin embargo, en el marco de referencia cebado, los eventos A y C son simultáneos, y el evento B ocurre en un momento anterior. Si A y B corresponden a los relojes que golpean en Los Ángeles y Nueva York respectivamente, entonces es claro que B debe ocurrir en un momento anterior en el cuadro cebado si efectivamente A y C son simultáneos en ese cuadro.
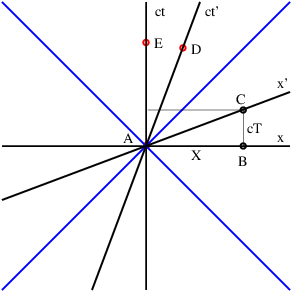
La línea inclinada que pasa por los eventos A y C en la figura 4.5 se llama la línea de simultaneidad para el marco de referencia cebado. Su pendiente está relacionada con la velocidad,\(U\), del marco de referencia por
\[slope = U ∕c (line of simultaneity). \label{4.4}\]
Observe que esta es la inversa de la pendiente de la línea mundial unida al marco de referencia cebado. Existe así una simetría entre la línea del mundo y la línea de simultaneidad de un marco de referencia móvil —a medida que el marco de referencia se mueve más rápido hacia la derecha, estas dos líneas se cierran como las cuchillas de un par de tijeras en la línea de 45°.
En la relatividad galilea es bastante obvio lo que queremos decir con dos eventos que son simultáneos: todo se reduce a coordinar relojes portátiles que están sentados uno al lado del otro, y luego moverlos a los lugares deseados. Dos eventos separados en el espacio son simultáneos si ocurren al mismo tiempo en relojes ubicados cerca de cada evento, asumiendo que los relojes han sido coordinados de la manera anterior.
En la relatividad einsteiniana esto no funciona, porque el acto mismo de mover los relojes cambia la velocidad a la que funcionan los relojes. Por lo tanto, es más difícil determinar si dos eventos distantes son simultáneos.
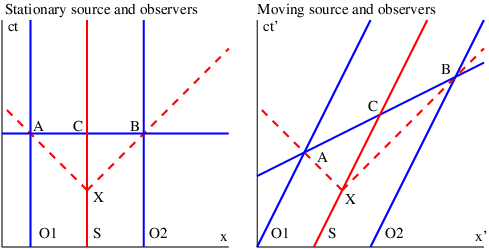
En la figura 4.6 se muestra una forma alternativa de determinar experimentalmente la simultaneidad. Dado que sabemos por observación que la luz viaja a la misma velocidad en todos los fotogramas de referencia, los pulsos de luz emitidos por las fuentes de luz en la figura 4.6 llegarán simultáneamente a los dos observadores equidistantes en ambos casos. La línea que pasa por estos dos eventos, A y B, define una línea de simultaneidad tanto para observadores estacionarios como móviles. Para los observadores estacionarios esta línea es horizontal, como en la relatividad galilea. Para los observadores en movimiento la luz tiene que viajar más lejos en el marco de reposo para llegar al observador retrocediendo de la fuente de luz y, por lo tanto, lleva más tiempo en este marco. Así, el evento B en el panel derecho de la figura 4.6 ocurre más tarde que el evento A en el marco de referencia estacionario y la línea de simultaneidad se inclina. Vemos que el postulado de que la luz se mueve a la misma velocidad en todos los marcos de referencia conduce inevitablemente a la dependencia de la simultaneidad en el marco de referencia.
Teorema de Pitágoras del espacio-tiempo
El teorema de Pitágoras del espacio-tiempo difiere del teorema habitual de Pitágoras en dos formas. Primero, el lado vertical del triángulo se multiplica por\(c\). Se trata de un factor de escala trivial que le da al tiempo las mismas unidades que al espacio. Segundo, el lado derecho de la ecuación 4.3} tiene un signo menos en lugar de un signo más. Esto resalta una diferencia fundamental entre el espacio-tiempo y el\(xyz \) espacio ordinario en el que vivimos. Se dice que el espacio-tiempo tiene una geometría no euclidiana (pero no curvada); en otras palabras, ¡las reglas normales de geometría que aprendemos en la secundaria no siempre funcionan para el espacio-tiempo!
La principal consecuencia del signo menos en la ecuación 4.3} es que\(I\) 2 puede ser negativo y por lo tanto\(I \) puede ser imaginario. Además, en el caso especial donde\(X \) = ±\(cT\), en realidad tenemos\(I \) = 0 aunque\(X,\)\( T\)\(≠\) 0 — i. e., la “distancia” entre dos eventos bien separados puede ser cero. Claramente, ¡el espacio-tiempo tiene algunas propiedades raras!
La cantidad\(I \) suele llamarse intervalo en espacio-tiempo. En términos generales, si\(I\) 2 es positivo, el intervalo se llama espacial, mientras que para un\(I\) 2 negativo, el intervalo se llama timelike.
Un concepto relacionado con el intervalo espacio-tiempo es el tiempo adecuado\(τ\). El tiempo adecuado entre los dos eventos A y C en la figura 4.4 se define por la ecuación
\[τ2 = T2 - X2 ∕c2. \label{4.5}\]
Observe que\(I \) y\(τ \) están relacionados por
\[τ2 = - I2∕c2, \label{4.6}\]
por lo que el intervalo espacio-tiempo y el tiempo adecuado no son conceptos independientes. Sin embargo,\(I \) tiene las dimensiones de longitud y es real cuando los eventos que definen el intervalo son espaciosos entre sí, mientras que\(τ \) tiene las dimensiones del tiempo y es real cuando los eventos son similares al tiempo entre sí. Tanto la ecuación 4.3} como la ecuación (4.5) expresan el teorema de Pitágoras del espacio-tiempo.
Si dos eventos que definen los puntos finales de un intervalo tienen el mismo\(t \) valor, entonces el intervalo es la distancia espacial ordinaria entre los dos eventos. Por otro lado, si tienen el mismo\(x \) valor, entonces el tiempo adecuado es solo el intervalo de tiempo entre los eventos. Si el intervalo entre dos eventos es espacial, pero los eventos no son simultáneos en el marco de referencia inicial, siempre se pueden hacer simultáneos eligiendo un marco de referencia en el que los eventos se encuentren en la misma línea de simultaneidad. Así, el significado del intervalo en ese caso es solo la distancia entre los eventos en el nuevo marco de referencia. De manera similar, para eventos separados por un intervalo similar al tiempo, el tiempo adecuado es solo el tiempo entre dos eventos en un marco de referencia en el que se colocan los dos eventos.
Dilatación
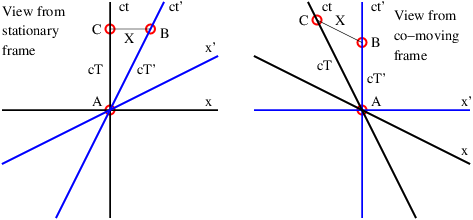
Los relojes estacionarios y móviles funcionan a diferentes velocidades en relatividad. Esto se ilustra en la figura 4.7. El triángulo ABC en el panel izquierdo de la figura 4.7 puede ser utilizado para ilustrar este punto. Supongamos que la línea que pasa por los eventos A y C en esta figura es la línea mundial de un observador estacionario. En tiempo cero otro observador que se mueve con velocidad\(V \) pasa al observador estacionario. La línea mundial del observador en movimiento pasa por los eventos A y B.
Suponemos que los eventos B y C son simultáneos en el resto del marco, por lo que ABC es un triángulo rectángulo. La aplicación del teorema de Pitágoras del espacio-tiempo rinde así
\[ 2 ′2 2 2 2 c T = cT - X . \label{4.7}\]
Como el segundo observador se mueve a velocidad\(V \), la pendiente de su línea mundial es
\[c cT V-= X--, \label{4.8}\]
donde el lado derecho de la ecuación anterior es la pendiente calculada como el ascenso de la línea mundial\(cT \) sobre la carrera\(X \) entre los eventos A y B. La eliminación\(X\) entre las dos ecuaciones anteriores da como resultado una relación entre\(T \) y\(T\) ′:
\[T′ = T(1 - V 2∕c2)1∕2 ≡ T ∕γ, \label{4.9}\]
donde
\[γ = ------1-------. (1 - V 2∕c2)1∕2 \label{4.10}\]
La cantidad\(γ \) ocurre tan a menudo en los cálculos relativistas que le damos este símbolo especial. Obsérvese por su definición que\(γ \) ≥ 1.
La ecuación (4.9) nos dice que el tiempo transcurrido para el observador en movimiento es menor que el del observador estacionario, lo que significa que el reloj del observador en movimiento corre más lentamente. Esto se llama el efecto de dilatación del tiempo.
Veamos esta situación desde el marco de referencia del observador en movimiento. En este marco el observador en movimiento se vuelve estacionario y el observador estacionario se mueve en la dirección opuesta, como se ilustra en el panel derecho de la figura 4.7. Por argumentos simétricos, se infiere que el reloj del observador inicialmente estacionario que ahora se mueve hacia la izquierda corre más lentamente en este marco de referencia que el reloj del observador inicialmente en movimiento. Se podría concluir que esto contradice los resultados anteriores. No obstante, el examen del panel derecho de la figura 4.7 muestra que esto no es así. El intervalo\(cT \) es aún mayor que el intervalo\(cT\) ′, debido a que tales intervalos son cantidades relativisticamente invariantes. Sin embargo, los eventos B y C ya no son simultáneos, por lo que no se pueden usar estos resultados para inferir nada sobre la velocidad a la que funcionan los dos relojes en este cuadro. Así, la naturaleza relativa del concepto de simultaneidad nos salva de una paradoja incipiente, y vemos que las velocidades relativas a las que corren los relojes dependen del marco de referencia en el que se observan estas velocidades.
Contracción Lorentz
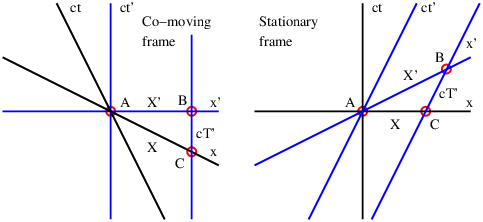
Se puede hacer un argumento similar para mostrar cómo los postulados de la relatividad resultan en la contracción de Lorentz. La Figura 4.8 compara la longitud\(X\) ′ de un objeto en movimiento medida en su propio marco de referencia (panel izquierdo) con su longitud\(X \) medida en un marco de referencia estacionario (panel derecho). La longitud de un objeto en movimiento se mide midiendo simultáneamente las posiciones de la parte delantera y trasera del objeto y restando estos dos números. Los eventos A y C corresponden a estas mediciones de posición para el marco de referencia estacionario ya que se encuentran respectivamente en las líneas mundiales trasera y delantera del objeto. Así, el intervalo AC, que es igual a\(X\), es la longitud del objeto medida en el marco estacionario.
En el panel izquierdo,\(X \) se encuentra la hipotenusa de un triángulo rectángulo. Por lo tanto, por el teorema de Pitágoras del espacio-tiempo, tenemos
\[X = I = (X ′2 - c2T′2)1∕2. \label{4.11}\]
Ahora, la línea que pasa por A y C en el panel izquierdo es la línea de simultaneidad del marco de referencia estacionario. La pendiente de esta línea es -\(V∕c\), donde\(V \) está la velocidad del objeto en relación con el marco de referencia estacionario. Geométricamente en la figura 4.8, la pendiente de esta línea es -\(cT\) ′\(∕X\) ′, por lo que encontramos al igualar estas dos expresiones para la pendiente que
\[ ′ ′ 2 T = VX ∕c . \label{4.12}\]
Finalmente, eliminar\(T\) ′ entre (4.11) y (4.12) da como resultado
\[X = X ′(1 - V 2∕c2)1∕2 = X ′∕γ. \label{4.13}\]
Esto dice que la longitud de un objeto en movimiento medida en un marco de referencia estacionario (\(X\)) es menor que la longitud real del objeto medida en su propio marco de referencia (\(X\)′). Esta reducción de longitud se llama contracción de Lorentz.
Tenga en cuenta que la contracción de Lorentz solo ocurre en la dirección del movimiento. Las dimensiones de un objeto en movimiento perpendiculares al movimiento permanecen sin cambios.
Paradoja
Una aplicación interesante de la dilatación del tiempo es la llamada paradoja de los gemelos, que resulta no ser una paradoja en absoluto. Dos gemelos tienen inicialmente la misma edad. Un gemelo viaja a una estrella distante en una nave espacial interestelar que se mueve a una velocidad\(V \) cercana a la velocidad de la luz. Al llegar a la estrella, el gemelo viajero inmediatamente se da la vuelta y se dirige a casa. Al llegar a casa, el gemelo viajero ha envejecido menos que el gemelo que se quedó en casa. Esto se explica fácilmente por el efecto de dilatación del tiempo, que demuestra que el tiempo adecuado transcurrido a lo largo de la línea mundial del gemelo viajero es (1 -\(V\)\(∕c\) 2 2) 1 2 veces el tiempo adecuado transcurrido a lo largo de la línea mundial del otro gemelo.
La parte “paradoja” de la paradoja gemela surge de hacer el argumento simétrico en el que se asume que el marco de referencia del gemelo viajero es estacionario. El marco del gemelo ligado a la tierra debe entonces viajar en el sentido opuesto al del antiguo gemelo viajero, lo que significa que el gemelo terrestre debe envejecer menos en lugar de más. Esta sustitución se justifica con base en el principio de relatividad, que establece que las leyes de la física deben ser las mismas en todos los marcos de referencia inerciales.
No obstante, el argumento anterior es falaz, porque el marco de referencia del gemelo viajero no es inercial a lo largo de todo el viaje, ya que en diversos puntos la nave espacial tiene que acelerar y desacelerar. Así, el principio de relatividad no puede utilizarse para afirmar la equivalencia del marco de referencia del viajero con el marco estacionario.
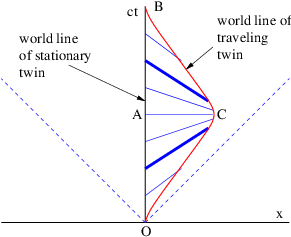
De particular importancia es el periodo de desaceleración y aceleración cerca de la estrella distante. Durante este intervalo, la línea de simulaneidad del gemelo viajero gira, como se ilustra en la figura 4.9, de tal manera que el gemelo que se queda en casa envejece rápidamente en el marco de referencia del viajero. Así, aunque la aceleración del gemelo viajero pueda ocupar solo un segmento insignificante de la línea mundial del gemelo, el efecto general no es despreciable. De hecho, cuanto más corto e intenso es el período de aceleración, ¡más rápidamente envejece el gemelo terrestre en el marco itinerante durante este intervalo!
Problemas
- Esboza tu línea mundial personal en un diagrama de espacio-tiempo durante las últimas 24 horas, etiquetando por tiempo y ubicación eventos especiales como comidas, clases de física, etc. Relacionar la pendiente de la línea mundial en varios momentos con lo rápido que estabas caminando, montando en un automóvil, etc.
- Conversiones espacio-tiempo:
- ¿Cuál es la distancia de Nueva York a Los Ángeles en segundos? ¿De aquí a la luna? ¿De aquí al sol?
- ¿Qué es un nanosegundo en metros? ¿Un segundo? ¿Un día? ¿Un año?
- Tres eventos tienen las siguientes coordenadas espacio-tiempo: A está en (\(x,ct\)) = (2 m\(, \) 1 m); B está en (\(x,ct\)) = (- 2 m\(, \) 0 m); C está en (\(x,ct\)) = (0 m\(, \) 3 m).
- Una línea mundial para un objeto pasa por los eventos B y C. ¿Qué tan rápido y en qué dirección se mueve el objeto?
- Una línea de simultaneidad para un sistema de coordenadas pasa por los eventos A y B. ¿Qué tan rápido y en qué dirección se mueve el sistema de coordenadas?
- ¿Cuál es el intervalo invariante entre los eventos A y B? B y C? A y C?
- ¿Puede una señal del evento B llegar al evento A? ¿Puede llegar al evento C? Explique.
Pista: Dibuja un diagrama de espacio-tiempo con todos los eventos trazados antes de intentar responder a las preguntas anteriores.
- En el siguiente problema asegúrese de indicar la pendiente de todas las líneas pertinentes dibujadas.
- En un diagrama de espacio-tiempo, esboce una línea de simultaneidad para un marco de referencia que se mueve hacia la izquierda en\(V \) =\(c∕\) 2, donde\(c \) está la velocidad de la luz.
- Esboza la línea mundial de un objeto que inicialmente es estacionario, pero que acelera a una velocidad de\(v \) =\(c∕\) 3.
- Si las pendientes de las líneas mundiales de los observadores en el panel derecho de la figura 4.6 son ambas 1\(∕β\), encuentra la pendiente de su línea de simultaneidad, AB.
- Supongamos que una nave espacial interestelar recorre una distancia\(X \) = 100 años luz en relación con el marco de descanso en\(T\) ′ = 10 años de su propio tiempo.
- Dibuje un diagrama de espacio-tiempo en el marco de descanso que muestre\(X\),\(T\) ′, y el tiempo\(T \) necesario para este viaje en relación con el marco de descanso.
- Compute\(T\), usando tu diagrama de espacio-tiempo como ayuda.
- Calcular la velocidad de la nave espacial.
- Si un piloto de aerolínea vuela 80 hr al mes (en el marco de descanso) a 300 m s - 1 durante 30 años, ¿cuánto más joven será que su hermano gemelo (que maneja equipaje) cuando se jubile? Pista: Usar (1 +\(ϵ\)) x ≈ 1 +\(xϵ \) para pequeños\(ϵ\).
- Una partícula mu normalmente vive alrededor de 2 × 10 - 6 segundos antes de que se descomponga. Sin embargo, los muones creados por los rayos cósmicos a 20 km de altura en la atmósfera alcanzan la superficie de la Tierra. ¿Qué tan rápido deben ir?
- El Acelerador Lineal de Stanford acelera los electrones a una velocidad tal que el acelerador de 3 km de largo parece tener 8 cm de largo al electrón, debido a la contracción de Lorentz. ¿Cuánto menos que la velocidad de la luz está viajando el electrón? Pista: Lo mejor es desarrollar primero una aproximación para la relación entre\(γ \) = (1 -\(v\) 2\(∕c\) 2) - 1 2 y la diferencia entre\(c \) y\(v \) para una partícula que se mueve cerca de la velocidad de la luz.
- ¿Qué tan rápido tienes que ir para llegar al centro de nuestra galaxia en tu vida esperada? A esta velocidad, ¿qué parece ser esta distancia? (Estamos a unos 30000 años luz del centro galáctico.)
- Dos naves espaciales idénticas se pasan entre sí yendo en dirección opuesta a la misma velocidad.
- Esboce un diagrama espacio-tiempo que muestre las líneas mundiales de la parte delantera y trasera de cada nave espacial, así como líneas de simultaneidad para cada nave espacial.
- Indique un intervalo en el diagrama correspondiente a la longitud de la nave espacial que se mueve hacia la derecha en su propio marco de referencia.
- Indicar un intervalo correspondiente a la longitud de la nave espacial que se mueve hacia la izquierda en el marco de referencia de la nave espacial que se mueve hacia la derecha.
- Indicar un intervalo igual a la longitud de cualquiera de las naves espaciales en el marco de descanso.
Figura 4.10: Croquis para gemelos móviles. Line AC es la línea de simultaneidad para un marco de referencia que se mueve con Sally y George.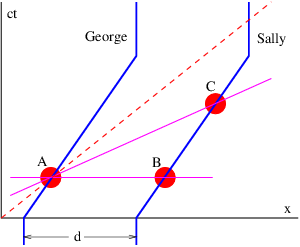
_____________________________________
- George y Sally son gemelos inicialmente separados por una distancia\(d \) y en reposo. En el resto marco inicialmente tienen la misma edad. Al tiempo\(t \) = 0 tanto George como Sally se meten en sus naves espaciales y se dirigen a la derecha a velocidad\(U\). Ambos se mueven una distancia\(d \) a la derecha y desaceleran a un alto. (Véase la figura 4.10.)
- Cuando ambos se mueven, ¿a qué distancia está Sally según George?
- ¿Cuánto mayor o menor es Sally relativa a George mientras ambos se mueven?
- ¿Cuánto mayor o menor es Sally relativa a George después de que ambos paren?
Sugerencia: Dibuja el triángulo ABC en un marco de referencia moviéndose con George y Sally.
Capítulo 5 Aplicaciones de la Relatividad Especial
En este capítulo continuamos el estudio de la relatividad especial. Aquí se hacen tres aplicaciones importantes de las ideas desarrolladas en el capítulo anterior. Primero, mostramos cómo describir las olas en el contexto del espacio-tiempo. Luego vemos cómo las ondas que no tienen un marco de referencia preferido (como la de un medio que las soporta) están restringidas por una relatividad especial para tener una relación de dispersión de una forma particular. Esta relación de dispersión resulta ser la de las ondas relativistas de materia de la mecánica cuántica. En segundo lugar, se investiga el fenómeno de desplazamiento Doppler, en el que la frecuencia de una onda adquiere diferentes valores en diferentes sistemas de coordenadas. En tercer lugar, mostramos cómo agregar velocidades de manera relativistamente consistente.
Se presenta una nueva idea matemática en el contexto de las ondas relativistas, a saber, el vector espacio-tiempo o cuatro vectores. Escribir las leyes de la física totalmente en términos de escalares relativistas y cuatro vectores asegura que serán válidas en todos los marcos de referencia inerciales.
Olas en el espacio-tiempo
Ahora nos fijamos en las características de las olas en el espacio-tiempo. Recordemos que una onda sinusoidal que se mueve hacia la derecha en una dimensión espacial puede ser representada por
\[A (x,t) = A0 sin (kx - ωt), \label{5.1}\]
donde\(A\) 0 es la amplitud (constante) de la onda,\(k \) es el número de onda, y\(ω \) es la frecuencia angular, y que la cantidad\(ϕ \) =\(kx \) -\(ωt \) se llama la fase de la onda. Para una onda plana en tres dimensiones espaciales, la onda se representa de manera similar,
\[A (x,t) = A sin (k ⋅ x - ωt), 0 \label{5.2}\]
donde\(x\) está ahora el vector de posición y\(k\) es el vector de onda. La magnitud del vector de onda, |\(k\) | =\(k \) es solo el número de onda de la onda y la dirección de este vector indica la dirección en la que se mueve la onda. La fase de la onda en este caso es\(ϕ \) =\(k\) ⋅\(x\) -\(ωt\).
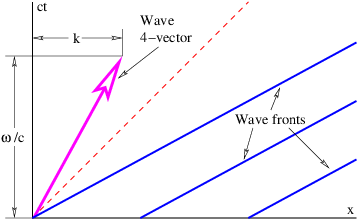
En el caso de una onda unidimensional que se mueve hacia la derecha\(ϕ \) =\(kx\) -\(ωt\). Un frente de onda tiene fase constante\(ϕ\), por lo que resolver esta ecuación para\(t \) y multiplicar por\(c\), la velocidad de la luz en un vacío, nos da una ecuación para la línea mundial de un frente de onda:
\[ ckx- cϕ- cx- cϕ- ct = ω - ω = up - ω (wave front ). \label{5.3}\]
La pendiente de la línea mundial en un diagrama de espacio-tiempo es el coeficiente de\(x\), o\(c∕u\) p, donde\(u\) p =\(ω∕k \) es la velocidad de fase. Las líneas mundiales de los frentes de onda de una ola se ilustran en la figura 5.1.
Tutorial — Cuatro vectores
También se muestra en la figura 5.1 un vector espacio-tiempo o cuatro vectores que representa la frecuencia y número de onda de la onda, a la que nos referimos como el cuatro vector de onda. Se llama cuatro vectores porque tiene 3 componentes espaciales y un componente tipo tiempo cuando hay 3 dimensiones de espacio. En el caso mostrado, solo hay una dimensión espacial única. El componente espacial del cuatro vector de onda es justo\(k\) (o\(k\) cuando hay 3 dimensiones de espacio), mientras que el componente de tipo tiempo lo es\(ω∕c\). El\(c \) está en el denominador para darle al componente timelike las mismas dimensiones que el componente espacial. De la figura 5.1 queda claro que la pendiente de la línea que representa el cuatro-vector es\(ω∕ck\), que es solo la inversa de la pendiente de los frentes de ola.
Definamos alguna terminología. Indicamos un cuatro vector subrayando y escribimos los componentes de la siguiente manera:\(k\) = (\(k,ω∕c\)), donde\(k\) está el cuatro vector de onda,\(k \) es su componente espacial y\(ω∕c \) es su componente temporal. Para tres dimensiones espaciales, donde tenemos un vector de onda en lugar de solo un número de onda, escribimos\(k\) = (\(k\)\(,ω∕c\)).
Otro ejemplo de cuatro vectores es simplemente el vector de posición en espacio-tiempo,\(x\) = (\(x,ct\)) o\(x\) = (\(x\)\(,ct\)) en tres dimensiones espaciales. El\(c \) multiplica el componente timelike en este caso, porque eso es lo que se necesita para darle las mismas dimensiones que el componente espacial.
En tres dimensiones definimos un vector como una cantidad con magnitud y dirección. Extendiendo esto al espacio-tiempo, un cuatro vector es una cantidad con magnitud y dirección en espacio-tiempo. Implícita en esta definición está la noción de que la magnitud del vector es una cantidad independiente del sistema de coordenadas o marco de referencia. Hemos visto que el intervalo invariante en el espacio-tiempo desde el origen hasta el punto (\(x,ct\)) es\(I \) = (\(x\)\(c\)2 -\(t\) 2 2) 1 2, por lo que tiene sentido identificarlo como la magnitud del vector de posición. Esto lleva a una forma de definir un producto punto de cuatro vectores. Dados dos cuatro vectores\(A\) = (\(A\)\(,A\)t) y\(B\) = (\(B\)\(,B\)t), el producto de punto es
\[A ⋅ B = A ⋅ B - A B (dot product in spacetime ). -- -- t t \label{5.4}\]
Esto es consistente con la definición de intervalo invariante si establecemos\(A\) =\(B\) =\(x\) , desde entonces\(x\) ⋅\(x\) =\(x\) 2 -\(c\) 2\(t\) 2 =\(I\) 2.
En la extraña geometría del espacio-tiempo no es obvio lo que significa “perpendicular”. Por lo tanto, definimos dos cuatro vectores\(A\) y\(B\) ser perpendiculares si su producto punto es cero,\(A\) ⋅\(B\) = 0, en analogía con vectores ordinarios.
El producto punto de dos cuatro vectores es un resultado escalar, es decir, su valor es independiente del sistema de coordenadas. Esto se puede utilizar a nuestro favor en ocasiones. Por ejemplo, considere el producto de punto de un cuatro vectores\(A\) que se resuelve en (\(A\)x\(,A\) t) en el marco no cebado. Supongamos además que el componente espacial es cero en algún fotograma cebado, de modo que los componentes en este fotograma son (0\(,A\) t′). El hecho de que el producto punto sea independiente del sistema de coordenadas significa que
\[ 2 2 ′2 A-⋅ A-= Ax - A t = - At . \label{5.5}\]
Esto constituye una extensión del teorema de Pitágoras espacio-tiempo a cuatro vectores distintos del vector de posición cuatro. Así, por ejemplo, el número de onda para alguna onda puede ser cero en la trama cebada, lo que significa que el número de onda y la frecuencia en la trama no cebada están relacionados con la frecuencia en la trama cebada por
\[k2 - ω2 ∕c2 = - ω ′2∕c2. \label{5.6}\]
Principio de Relatividad Aplicada
Volviendo a la fase de una ola, inmediatamente vemos que
\[ϕ = k ⋅ x - ωt = k ⋅ x - (ω∕c)(ct) = k ⋅ x. \label{5.7}\]
Por lo tanto, una forma compacta de reescribir la ecuación 5.2} es
\[A (x) = A0 sin(k-⋅ x). \label{5.8}\]
Dado que\(x\) se sabe que es un cuatro vector y dado que se sabe que la fase de una onda es un escalar independiente del marco de referencia, se deduce que también\(k\) es un cuatro vector en lugar de solo un conjunto de números. Por lo tanto, el cuadrado de la longitud de la onda de cuatro vectores también debe ser un escalar independiente del marco de referencia:
\[ 2 2 k ⋅ k-= k ⋅ k - ω ∕c = const. \label{5.9}\]
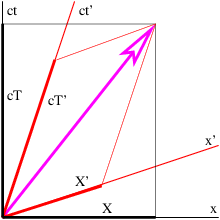
Revisemos precisamente lo que esto significa. Como muestra la figura 5.2, podemos resolver una posición de cuatro vectores en componentes en dos marcos de referencia diferentes,\(x\) = (\(X,cT\)) = (\(X\)′\(,cT\) ′). Sin embargo, aunque\(X\)\(≠\)\(X\) ′ y\(T\)\(≠\)\(T\) ′, las longitudes vectoriales calculadas a partir de estos dos conjuntos de componentes son necesariamente las mismas:\(x\) ⋅\(x\) =\(X\) 2 -\(c\) 2\(T\) 2 =\(X\) ′ 2 -\(c\) 2\(T\) ′ 2 .
Aplicando esto a la onda de cuatro vectores, inferimos que
\[ 2 2 2 ′2 ′2 2 k - ω ∕c = k - ω ∕c = const., \label{5.10}\]
donde los valores no cebados y cebados de\(k \) y\(ω \) se refieren a los componentes de la onda de cuatro vectores en dos marcos de referencia diferentes.
Hasta ahora, este argumento se aplica a cualquier ola. Sin embargo, las ondas se pueden dividir en dos categorías, aquellas para las que existe un marco de referencia “especial” y aquellas para las que no existe tal marco especial. Como ejemplo de lo primero, las ondas sonoras se ven más simples en el marco de referencia en el que el gas que transporta el sonido es estacionario. Lo mismo ocurre con la luz que se propaga a través de un medio material con un índice de refracción no igual a la unidad. En ambos casos la velocidad de la ola es la misma en todas las direcciones solo en el marco en el que el medio material es estacionario.
Supongamos que tenemos una máquina que produce una onda con número de onda\(k \) y frecuencia\(ω \) en su propio marco de descanso. Si observamos la onda desde un marco de referencia móvil, el número de onda y la frecuencia serán diferentes, digamos,\(k\) ′ y\(ω\) ′. Sin embargo, estas cantidades estarán relacionadas por la ecuación 5.10}.
Hasta este punto el argumento se aplica a cualquier onda ya sea que exista o no un marco de referencia especial; los cambios observados en el número de onda y la frecuencia no tienen nada que ver con la onda misma, sino que son solo consecuencias de cómo hemos optado por observarla. Sin embargo, si no hay un marco de referencia especial para el tipo de onda en consideración, entonces se puede obtener el mismo resultado manteniendo al observador estacionario y moviendo la máquina productora de olas en la dirección opuesta. Al moverlo a varias velocidades, se puede obtener cualquier valor deseado de\(k\) ′ en el marco de referencia inicial (a diferencia de algún otro fotograma), y el valor resultante de\(ω\) ′ se puede calcular usando la ecuación 5.10}.
Este es en realidad un resultado asombroso. Hemos demostrado sobre la base del principio de relatividad que cualquier tipo de onda para el que no exista un marco de referencia especial puede hacerse para tomar una gama completa de frecuencias y números de onda en cualquier marco de referencia dado, y además que estas frecuencias y números de onda obedecen
\[ 2 2 2 2 ω = k c + μ . \label{5.11}\]
La ecuación (5.11) proviene de resolver la ecuación 5.10} para\(ω\) 2 y la constante\(μ\) 2 es igual a la constante en la ecuación (5.10) veces -\(c\) 2. La ecuación (5.11) relaciona la frecuencia con el número de onda y, por lo tanto, es la relación de dispersión para tales ondas. Llamamos ondas que no tienen marco de referencia especial y por lo tanto obedecen necesariamente a la ecuación (5.11) ondas relativistas. La única diferencia en las relaciones de dispersión entre diferentes tipos de ondas relativistas es el valor de la constante\(μ\). El significado de esta constante se aclarará más adelante.
Características de las Ondas Relativistas
La luz en el vacío es un ejemplo de una onda para la que no existe ningún marco de referencia especial. Para la luz,\(μ \) = 0, y tenemos (tomando la raíz positiva)\(ω \) =\(ck\). Esto simplemente afirma lo que ya sabemos, es decir, que la velocidad de fase de la luz en un vacío es\(c\).
Si\(μ\)\(≠\) 0, las ondas de este tipo son dispersivas. La velocidad de fase es
\[ ω up = --= (c2 + μ2∕k2 )1∕2. k \label{5.12} \]
Esta velocidad de fase siempre supera\(c\), lo que al principio parece una conclusión poco física. Sin embargo, la velocidad de grupo de la onda es
\[ 2 2 2 ug = d-ω = -----c-k------= kc--= c-, dk (k2c2 + μ2)1∕2 ω up \label{5.13} \]
que siempre es menor que\(c\). Dado que los paquetes de ondas y por lo tanto las señales se propagan a la velocidad de grupo, las ondas de este tipo son físicamente razonables aunque la velocidad de fase exceda la velocidad de la luz.
Otra propiedad interesante de tales ondas es que la onda de cuatro vectores es paralela a la línea mundial de un paquete de ondas en el espacio-tiempo. Esto se demuestra fácilmente por el siguiente argumento. Como muestra la figura 5.1, el componente espacial de una onda de cuatro vectores es\(k\), mientras que el componente temporal lo es\(ω∕c\). Por lo tanto, la pendiente de los cuatro vectores en un diagrama de espacio-tiempo es\(ω∕kc\). Sin embargo, la pendiente de la línea mundial de un paquete de olas que se mueve con velocidad de grupo\(u\) \(c∕u\)g es g =\(ω∕\) (\(kc\)), que es la misma que la pendiente del\(k\) cuatro vector.
Tenga en cuenta que cuando\(k \) = 0 tenemos\(ω \) =\(μ\). En este caso la velocidad de grupo de la onda es cero. Por esta razón llamamos a\(μ \) la frecuencia de descanso de la onda.
Desplazamiento Doppler
Probablemente hayas escuchado cómo cambia el tono de una bocina de tren a medida que te pasa. Cuando el tren se acerca, el tono o frecuencia es mayor que cuando se aleja de ti. A esto se le llama el cambio Doppler. Un cambio similar, pero distinto ocurre si te estás moviendo más allá de una fuente de sonido. Si suena un silbato estacionario, el tono percibido desde un automóvil en movimiento es más alto mientras se mueve hacia la fuente que cuando se aleja. El primer caso tiene así una fuente móvil, mientras que el segundo caso tiene un observador en movimiento.
En esta sección calculamos el desplazamiento Doppler tal como se aplica a la luz que se mueve a través de un vacío. La Figura 5.3 muestra la geometría para calcular el tiempo entre los frentes de onda de luz para un marco de referencia estacionario y uno móvil. El tiempo en el marco estacionario es justo\(T\). Dado que las líneas mundiales de los frentes de ola tienen una pendiente de unidad, los lados del triángulo sombreado tienen el mismo valor,\(X\). Si el observador se mueve a velocidad\(U\), la pendiente de la línea mundial del observador es\(c∕U\), lo que significa que\(c∕U \) = (\(cT \)+\(X\))\(∕X\). Resolviendo esto para\(X \) rendimientos\(X \) =\(UT∕\) (1 -\(U∕c\)), que luego se puede utilizar para calcular\(T\) ′ =\(T \) +\(X∕c \) =\(T∕\) (1 -\(U∕c\)). Esta fórmula tal como está conduce al clásico desplazamiento Doppler para un observador en movimiento. Sin embargo, con las velocidades relativistas, hay que tener en cuenta un factor adicional: El observador experimenta dilatación en el tiempo ya que se está moviendo. El tiempo real medido por el observador entre los frentes de onda es en realidad
\[ ( )1 ∕2 ′2 2 21∕2 (1 --U-2∕c2)1∕2 -1 +-U-∕c τ = (T - X ∕c ) = T 1 - U∕c = T 1 - U ∕c , \label{5.14} \]
donde el último paso usa 1 -\(U\) 2\(∕c\) 2 = (1 -\(U∕c\)) (1 +\(U∕c\)). De esto inferimos la fórmula relativista de desplazamiento Doppler para la luz en un vacío:
\[ ( 1 - U∕c )1∕2 ω ′ = ω -------- , 1 + U∕c \label{5.15} \]
donde la frecuencia medida por el observador móvil es\(ω\) ′ = 2\(π∕τ \) y la frecuencia observada en el cuadro estacionario es\(ω \) = 2\(π∕T\).
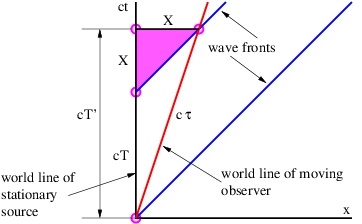
Podríamos continuar para determinar el desplazamiento Doppler resultante de una fuente móvil. Sin embargo, por el principio de relatividad, las leyes de la física deben ser las mismas en el marco de referencia en el que el observador está estacionario y la fuente se mueve. Además, la velocidad de la luz aún está\(c \) en ese cuadro. Por lo tanto, el problema de un observador estacionario y una fuente móvil es conceptualmente el mismo que el problema de un observador en movimiento y una fuente estacionaria cuando la onda se mueve a velocidad\(c\). Esto es diferente al caso de, digamos, las ondas sonoras, donde el observador estacionario y la fuente estacionaria producen diferentes fórmulas para el desplazamiento Doppler.
Adición de Velocidades
La Figura 5.4 muestra la línea mundial de un objeto en movimiento desde el punto de vista de dos marcos de referencia diferentes, con el marco imprimado (panel izquierdo) moviéndose hacia la derecha a velocidad\(U \) relativa al marco no imprimado (panel derecho). El objetivo es calcular la velocidad del objeto en relación con el cuadro no cebado\(v\), asumiendo su velocidad en el cuadro cebado,\(v\) ′ es conocida. El resultado clásico es simplemente
\[v = U + v′ (classical result). \label{5.16}\]
Sin embargo, esto es inconsistente con que la velocidad de la luz sea constante en todos los fotogramas de referencia, ya que si\(c \) sustituimos\(v\) ′, esta fórmula predice que la velocidad de la luz en el fotograma no cebado es\(U \) +\(c\).
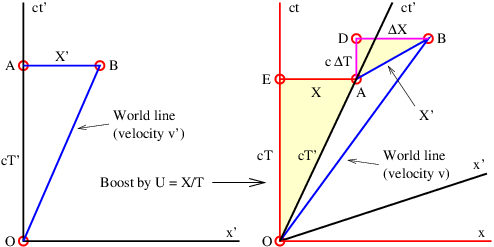
Podemos usar la geometría de la figura 5.4 para llegar a la fórmula relativista correcta. Del panel derecho de esta figura inferimos que
\[v-= X--+-ΔX---= X-∕(cT)-+-ΔX--∕(cT). c cT + cΔT 1 + ΔT ∕T \label{5.17}\]
Esto se deduce del hecho de que la pendiente de la línea mundial del objeto en este marco es\(c∕v\). La pendiente se calcula como la relación de la subida,\(c\) (\(T \)+ Δ\(T\)), a la carrera,\(X \) + Δ\(X\).
Desde el panel izquierdo de la figura 5.4 vemos de manera similar que
\[v′ X ′ --= --′. c cT \label{5.18} \]
Sin embargo, podemos aplicar nuestros cálculos de contracción de Lorentz y dilatación temporal del capítulo anterior a los triángulos ABD y OAE en el panel derecho. La pendiente de AB se\(U∕c \) debe a que AB es horizontal en el panel izquierdo, por lo que\(X\) ′ = Δ\(X\) (1 -\(U\)\(∕c\) 2 2) 1 2. De igual manera, la pendiente de OA es\(c∕U \) ya que OA es vertical en el panel izquierdo, y\(T\) ′ =\(T\) (1 -\(U\)\(∕c\) 2 2) 1 2. Sustituir estas fórmulas en la ecuación por\(v\) ′\(∕c \) rendimientos
\[v′ ΔX -- = ----. c cT \label{5.19} \]
Nuevamente usando lo que sabemos de los triángulos ABD y OAE, vemos que
\[U-= cΔT--= X--. c ΔX cT \label{5.20}\]
Finalmente, calculamos Δ\(T∕T \) al notar que
\[ΔT ΔT cΔX ( cΔT ) ( ΔX ) U v′ ----= --------- = ----- ---- = -- --. T T cΔX ΔX cT c c \label{5.21} \]
Sustituir las ecuaciones (5.19), (5.20) y (5.21) en la ecuación 5.17} y simplificar produce la fórmula relativista de adición de velocidad:
\[ ′ v = --U-+-v---- (special relativity). 1 + U v′∕c2 \label{5.22} \]
Observe cómo se comporta esta ecuación en diversos límites. Si |\(Uv\)\(c\) ′|2, el denominador de la ecuación (5.22) es casi la unidad, y la fórmula relativista especial se reduce al caso clásico. Por otro lado, si\(v\) ′ =\(c\), entonces la ecuación (5.22) reduce a\(v \) =\(c\). Es decir, si el objeto en cuestión se mueve a la velocidad de la luz en un marco de referencia, se mueve a la velocidad de la luz en todos los marcos de referencia, es decir, para todos los valores posibles de\(U\). Así, hemos encontrado una fórmula de adición de velocidad que 1) reduce a la fórmula clásica para bajas velocidades y 2) da los resultados observados para velocidades muy altas también.
La ecuación (5.22) es válida incluso si\(v\) ′ es negativa, es decir, si el objeto se mueve hacia la derecha con menor rapidez que el marco de referencia cebado, o incluso si se mueve hacia la izquierda en el fotograma no cebado.
Problemas
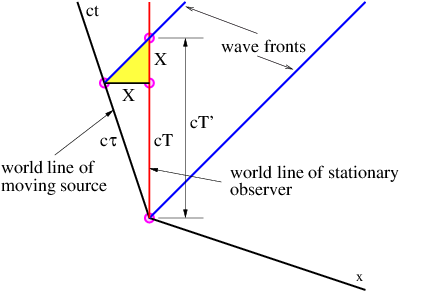
- Esboce los frentes de onda y los\(k\) cuatro vectores en un diagrama de espacio-tiempo para el caso donde\(ω∕k \) = 2\(c\). Etiquete sus ejes y espacie los frentes de onda correctamente para la caja\(k \) = 4\(π\) m - 1.
- Si el cuatro vector\(k\) = (0\(, \) 1 nm - 1) en el resto del cuadro, encuentre los componentes de espacio y tiempo de\(k\) en un cuadro moviéndose hacia la izquierda a velocidad\(c∕\) 2.
- Examinemos los cuatro vectores\(u\) = (\(u\)g\(,c\))\(∕\) (1 -\(β\) 2) 1 2 donde\(β \) =\(u\) g \(∕c\),\(u\) g siendo la velocidad de algún objeto. El cuatro-vector\(u\) se llama la velocidad de cuatro.
- Espectáculo que\(u\) es paralelo a la línea mundial del objeto.
- Mostrar que\(u\) ⋅\(u\) = -\(c\) 2.
- Si\(u\) g es la velocidad de grupo de un paquete de ondas relativistas, muestre que\(k\) = (\(μ∕c\)2)\(u\) , donde\(k\) está la onda central de cuatro vectores del paquete de ondas.
- Encuentra el desplazamiento Doppler para una fuente de luz móvil de la figura 5.5, siguiendo aproximadamente el procedimiento utilizado en el texto para encontrar el desplazamiento de un observador en movimiento. (Supongamos que la fuente se mueve hacia la izquierda a velocidad\(U\).) ¿El resultado es el mismo que para el observador en movimiento, como lo exige el principio de relatividad?
- Encuentre el desplazamiento Doppler para una fuente estacionaria de sonido (\(c \)≈ 380 m s - 1 en una atmósfera estacionaria) medido por un observador en movimiento. Siga el procedimiento como para la luz en la sección 5.5 excepto tenga en cuenta que el tiempo adecuado\(τ \) es prácticamente el mismo que el tiempo\(T\) ′ en la figura 5.3 ya que las velocidades son mucho menores que la velocidad de la luz.
- Supongamos que haces brillar un láser con frecuencia\(ω \) y número de onda\(k \) en un espejo que se mueve hacia ti a velocidad\(v\), como se ve en la figura 5.6. ¿Cuáles son la frecuencia\(ω\) ′ y el número de onda\(k\) ′ del haz reflejado? Pista: Encuentra la frecuencia del haz incidente en el marco de referencia del espejo. La frecuencia del haz reflejado será la misma que la del haz incidente en este marco. Después transforma de nuevo al marco de referencia del láser.
Figura 5.6: Haz láser que se refleja en un espejo en movimiento.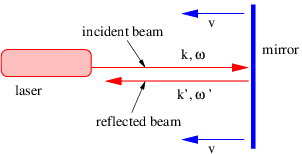
_____________________________________
- Supongamos que el gemelo en movimiento en la paradoja de los gemelos tiene un poderoso telescopio para que pueda ver a su hermano gemelo de regreso a la tierra durante todo el viaje. Describa cómo el gemelo terrestre parece envejecer al gemelo itinerante en comparación con su propia tasa de envejecimiento. Use un diagrama de espacio-tiempo para ilustrar su argumento y considere por separado los tramos de salida y retorno. ¡Recuerda que la luz viaja a la velocidad de la luz! Pista: ¿El concepto de cambio Doppler ayuda aquí?
- Encuentre la velocidad de un objeto con respecto al fotograma de reposo si se mueve a una velocidad de 0\(.\) 1\(c \) con respecto a otro fotograma que a su vez se mueve en la misma dirección a 0\(.\) 1\(c \) con respecto al fotograma de descanso usando
- la fórmula galilea y
- la fórmula de la relatividad especial.
Determine el error fraccionario realizado al usar la fórmula galilea.
- Cada etapa de un cohete de 3 etapas de alto rendimiento puede acelerar a una velocidad de 0\(.\) 9\(c \) desde el reposo. Si el cohete parte del reposo, ¿qué tan rápido va finalmente la etapa final?
- Una nave espacial interestelar va de la Tierra a Sirio con velocidad\(U \) = 0\(.\) 8\(c\) relativa al marco de descanso. Pasa una nave espacial que va de Sirio a la Tierra a una velocidad de 0\(.\) 95\(c \) en el marco de referencia de la primera nave espacial. ¿Cuál es la velocidad (dirección y velocidad) de la segunda nave espacial en el marco de descanso?
Capítulo 6 Aceleración y Relatividad General
La relatividad general es la extensión de Einstein de la relatividad especial para incluir la gravedad. Un aspecto importante de la relatividad general es que el espacio-tiempo ya no es necesariamente plano, sino que de hecho puede ser curvo bajo la influencia de la masa. Comprender el espacio-tiempo curvo es un tema avanzado que no es fácilmente accesible a nivel de este texto. Sin embargo, resulta que se puede obtener alguna idea de los fenómenos relativistas generales investigando los efectos de la aceleración en el espacio plano (pero no euclidiano) de la relatividad especial.
El supuesto central de la relatividad general es el principio de equivalencia, que establece que la gravedad es una fuerza que surge de estar en un marco de referencia acelerado. Para entender esto debemos investigar primero el concepto de aceleración. Luego vemos cómo esto conduce a fenómenos como el desplazamiento al rojo gravitacional, los horizontes de eventos y los agujeros negros. También introducimos de manera preliminar las nociones de fuerza y masa.
Aceleración
Imagina que estás en un potente auto de lujo parado en un semáforo. Mientras te sientas ahí, la gravedad te empuja hacia el cómodo asiento de cuero. La luz se vuelve verde y lo “piso”. El auto acelera y una fuerza adicional te empuja hacia el respaldo del asiento. Redondea una curva, y otra fuerza te empuja hacia el exterior de la curva. (¡Pero el asiento y el cinturón de seguridad bien diseñados te impiden sentir molestias!)
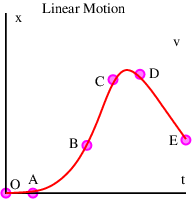
Examinemos más de cerca la idea de aceleración. Considerando la primera aceleración en una dimensión, la figura 6.1 muestra la posición de un objeto en función del tiempo,\(x\) (\(t\)). La velocidad es simplemente la tasa de tiempo de cambio de la posición:
\[ dx(t) v(t) = dt . \label{6.1}\]
La aceleración es la tasa de tiempo de cambio de velocidad:
\[ dv(t) d2x-(t) a(t) = dt = dt2 . \label{6.2}\]
En la figura 6.1, solo el segmento OA tiene velocidad cero. La velocidad está aumentando en AB, y la aceleración es positiva allí. La velocidad es constante en BC, lo que significa que la aceleración es cero. La velocidad disminuye en CD y la aceleración es negativa. Finalmente, en DE, la velocidad es negativa y la aceleración es cero.
En dos o tres dimensiones, la posición\(x\)\(v\), la velocidad y la aceleración\(a\) son todos vectores, de modo que la velocidad es
\[ dx(t) v(t) = ------ dt \label{6.3} \]
mientras que la aceleración es
\[ dv(t) a(t) = -----. dt \label{6.4} \]
Por lo tanto, en un corto intervalo de tiempo Δ\(t\), los cambios en\(x\) y se\(v\) pueden escribir
\[Δx = v Δt Δv = aΔt. \label{6.5}\]
Se trata de ecuaciones vectoriales, por lo que las restaciones que implican las operaciones “delta” deben hacerse vectorialmente. Un ejemplo donde la naturaleza vectorial de estas cantidades es importante es el movimiento en círculo a velocidad constante, que se discute en la siguiente sección.
Movimiento Circular
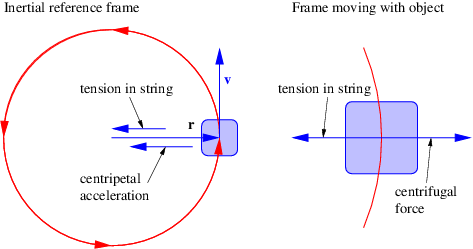
Imagine un objeto restringido por una cuerda unida para moverse en círculo a velocidad constante, como se muestra en el panel izquierdo de la figura 6.2. Ahora demostramos que la aceleración del objeto es hacia el centro del círculo. La aceleración en este caso especial se llama aceleración centrípeta.
La Figura 6.3 muestra la posición del objeto en dos tiempos espaciados por el intervalo de tiempo Δ\(t\). El vector de posición del objeto relativo al centro del círculo gira a través de un ángulo Δ\(θ \) durante este intervalo, por lo que la velocidad angular de revolución del objeto alrededor del centro es\(ω \) = Δ\(θ∕\) Δ\(t\). La magnitud de la velocidad del objeto es\(v\), por lo que el objeto se mueve una distancia\(v\) Δ\(t \) durante el intervalo de tiempo. En la medida en que esta distancia sea pequeña en comparación con el radio\(r \) del círculo, el ángulo Δ\(θ \) =\(v\) Δ\(t∕r\). Resolviendo para\(v \) y usando\(ω \) =\(θ∕\) Δ Δ\(t\), vemos que
\[v = ωr (circular motion ). \label{6.6}\]
La dirección del vector de velocidad cambia a lo largo de este intervalo, aunque la magnitud\(v \) se mantenga igual. La Figura 6.3 muestra que este cambio de dirección implica una aceleración\(a \) que se dirige hacia el centro del círculo, como se señaló anteriormente. La magnitud del cambio vectorial en la velocidad en el intervalo de tiempo Δ\(t \) es\(a\) Δ\(t\). Dado que el ángulo entre las velocidades inicial y final es el mismo que el ángulo Δ\(θ \) entre los vectores de radio inicial y final, vemos a partir de la geometría del triángulo en la figura 6.3 que\(a\) Δ\(t∕v \) = Δ\(θ\). Resolviendo\(a \) resultados en
\[a = ωv (circular motion ). \label{6.7}\]
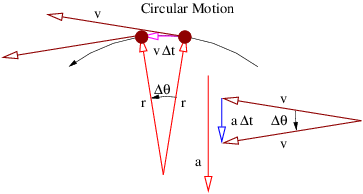
Combinando las ecuaciones (6.6) y (6.7) se obtiene la ecuación para la aceleración centrípeta:
\[a = ω2r = v2∕r (centripetal acceleration ). \label{6.8}\]
La segunda forma se obtiene eliminando\(ω \) de la primera forma usando la ecuación 6.6}.
Aceleración, Fuerza y Masa
Tenemos una buena sensación intuitiva para los conceptos de fuerza y masa porque son muy parte de nuestra experiencia cotidiana. Pensamos en la fuerza como lo duro que presionamos en algo. La masa es la resistencia de un objeto a la aceleración si de otra manera es libre de moverse. Por lo tanto, empujar una bicicleta en una carretera lisa y nivelada hace que acelere más fácilmente que empujar un automóvil. Decimos que el auto tiene mayor masa. Podemos resumir esta relación con la segunda ley de Newton
\[F = ma \label{6.9}\]
donde\(F \) es la fuerza total sobre un objeto,\(m \) es su masa, y\(a \) es la aceleración resultante de la fuerza.
Tres condiciones se aplican a la ecuación 6.9}. Primero, sólo tiene sentido en forma no modificada cuando la velocidad del objeto es mucho menor que la velocidad de la luz. Para las velocidades relativistas lo mejor es escribir esta ecuación en una forma ligeramente diferente que introducimos más adelante. Segundo, la fuerza debe ser la fuerza total, incluyendo todas las fuerzas de fricción y otras fuerzas incidentales que de otro modo podrían ser descuidadas por un observador acrítico. Tercero, sólo funciona en un marco de referencia que a su vez no está acelerado, es decir, un marco de referencia inercial. A continuación tratamos los marcos de referencia acelerados.
Aceleración en Relatividad Especial
Como se señaló anteriormente, la aceleración es solo la tasa de cambio de velocidad en el tiempo. Utilizamos los resultados anteriores para determinar cómo la aceleración se transforma de un marco de referencia a otro. La Figura 6.4 muestra la línea mundial de un marco de referencia acelerado, con una velocidad variable en el tiempo\(U\) (\(t\)) en relación con el marco de reposo inercial no cebado. Definiendo Δ\(U \) =\(U\) (\(T\)) -\(U\) (0) como el cambio en la velocidad del cuadro acelerado (relativo al fotograma no cebado) entre los eventos A y C, podemos relacionarlo con el cambio de velocidad, Δ\(U\) ′, del cuadro acelerado relativo a un marco inercial que se mueve con la velocidad inicial,\(U\) (0). Aplicando la ecuación para la adición relativista de velocidades, encontramos
\[ U (0) + ΔU ′ U(T ) = U(0) + ΔU = ------------′--2. 1 + U (0 )ΔU ∕c \label{6.10} \]
Observamos ahora que la aceleración media del marco de referencia entre los eventos A y C en el resto del fotograma es justamente\(a \) = Δ\(U∕T\), mientras que la aceleración media en el fotograma cebado entre los mismos dos eventos es\(a\) ′ = Δ\(U\) ′ ′\(∕T\) ′. De la ecuación 6.10} encontramos que
\[ ΔU ′[1 - U (0 )2∕c2] ΔU = -------------′--2-, 1 + U (0)ΔU ∕c \label{6.11} \]
y la aceleración del marco de referencia cebado tal como aparece en el fotograma no cebado es
\[ ΔU ΔU ′[1 - U (0)2∕c2] a = ----= -------------------. T T [1 + U (0)ΔU ′∕c2] \label{6.12} \]
Ya que nos interesa la aceleración instantánea más que la media, dejamos que\(T \) se hagan pequeños. Esto tiene tres consecuencias. Primero, Δ\(U\) y Δ\(U\) ′ se vuelven pequeños, lo que significa que el término\(U\) (0) Δ\(U\) ′\(∕c\) 2 en el denominador de la ecuación 6.12} puede ignorarse en comparación con 1. Esto significa que
\[ ′ 2 2 a ≈ ΔU--[1---U-(0)-∕c-], T \label{6.13} \]
con la aproximación llegando a ser exacta como\(T \) → 0. Segundo, el “triángulo” con el lado curvo en la figura 6.4 se convierte en un verdadero triángulo, con el resultado de que\(T\) ′ =\(T\) [1 -\(U\) (0) \(∕c\)2 2] 1 2 . Por lo tanto, se puede escribir la aceleración del cuadro imprimado con respecto a un marco inercial que se mueve a velocidad\(U\) (0)
\[ ′ ΔU ′ ΔU ′ a = ---′-= -----------2--21∕2. T T [1 - U (0) ∕c ] \label{6.14} \]
Tercero, podemos reemplazar\(U\) (0) con\(U\), ya que la velocidad del fotograma acelerado no cambia mucho en un corto intervalo de tiempo.
Dividir la ecuación 6.13} por la ecuación (6.14) da como resultado una relación entre las dos aceleraciones:
\[a = a′(1 - U2∕c2)3∕2, \label{6.15}\]
que muestra que la aceleración de un objeto que se mueve rápidamente\(a\), como se observa desde el fotograma de reposo, es menor que su aceleración relativa a un marco de referencia inercial en el que el objeto está casi estacionario,\(a\) ′, por el factor (1 -\(U\) 2\(∕c\) 2) 3 2. Llamamos a esta última aceleración la aceleración intrínseca. Esta diferencia en la aceleración observada entre los dos marcos de referencia inerciales es puramente el resultado de la geometría del espacio-tiempo, pero tiene consecuencias interesantes.
Identificándose\(a \) con\(dU∕dt\), podemos integrar la ecuación de aceleración asumiendo que la aceleración intrínseca\(a\) ′ es constante y que la velocidad\(U \) = 0 en el tiempo\(t \) = 0. Obtenemos el siguiente resultado (verificar esto diferenciando con respecto al tiempo):
\[a′t = ------U-------, (1 - U 2∕c2)1∕2 \label{6.16}\]
que podrán resolverse para\(U∕c\):
\[ ′ U-= -----a-t∕c-----. c [1 + (a′t∕c)2]1∕2 \label{6.17} \]
Esto se traza en la figura 6.5. Clásicamente, la velocidad\(U \) alcanzaría la velocidad de la luz cuando\(a\) ′\(t∕c \) = 1. Sin embargo, como muestra la figura 6.5, la velocidad a la que la velocidad aumenta con el tiempo se ralentiza a medida que el objeto se mueve más rápido, de tal manera que se\(U \) acerca\(c\) asintóticamente, pero nunca lo alcanza.
Los resultados de esta sección son válidos solo para componentes de aceleración en la dirección del movimiento. Los componentes perpendiculares a esta dirección se comportan de manera diferente y se tratan en textos más avanzados.
Marcos de referencia acelerados
Refiriéndose de nuevo a las fuerzas que siente el ocupante de un automóvil, es evidente que las fuerzas asociadas a las aceleraciones son dirigidas opuestas a las aceleraciones y proporcionales a sus magnitudes. Por ejemplo, al acelerar alejándose de un semáforo, la aceleración es hacia adelante y la fuerza percibida es hacia atrás. Al girar una esquina, la aceleración es hacia la esquina mientras que la fuerza percibida está alejada de la esquina. Tales fuerzas se llaman fuerzas inerciales.
El origen de estas fuerzas se puede entender determinando cómo cambia la aceleración cuando se observa desde un marco de referencia que a su vez se acelera. Supongamos que el marco de referencia cebado está acelerando hacia la derecha con aceleración\(A \) relativa al fotograma no cebado. La posición\(x\) ′ en el marco imprimado se puede relacionar con la posición\(x \) en el marco no cebado mediante
\[x = x′ + X, \label{6.18}\]
donde\(X \) es la posición del origen del fotograma imprimado en el fotograma no cebado. Tomando la segunda derivada de tiempo, vemos que
\[ ′ a = a + A, \label{6.19}\]
donde\(a \) =\(d\) 2\(x∕dt\) 2 es la aceleración en el cuadro no cebado y\(a\) ′ =\(d\) 2\(x\) ′\(∕dt\) 2 es la aceleración según un observador en el fotograma cebado.
Ahora sustituimos esto en la ecuación 6.9} y movemos el término que implica\(A \) al lado izquierdo:
\[F - mA = ma ′. \label{6.20}\]
Esto demuestra que la segunda ley de Newton representada por la ecuación 6.9} no es válida en un marco de referencia acelerado, porque la fuerza total\(F \) y la aceleración\(a\) ′ en este fotograma no se equilibran como lo hacen en el marco no acelerado; el término adicional -\(mA \) estropea este equilibrio.
Podemos solucionar este problema considerando -\(mA \) ser un tipo de fuerza, en cuyo caso podemos incluirla como parte de la fuerza total\(F\). Esta es la fuerza inercial que mencionamos anteriormente. Así, para resumir, podemos hacer que la segunda ley de Newton funcione cuando se observan objetos a partir de marcos de referencia acelerados si incluimos como parte de la fuerza total una fuerza inercial que es igual a -\(mA\),\(A \) siendo la aceleración del marco de referencia del observador y\(m \) la masa del objeto que se observa.
El panel derecho de la figura 6.2 muestra la fuerza inercial observada en el marco de referencia de un objeto que se mueve en movimiento circular a velocidad constante. En el caso del movimiento circular la fuerza inercial se denomina fuerza centrífuga. Señala lejos del centro del círculo y apenas equilibra la tensión en la cuerda. Esto hace que la fuerza total sobre el objeto sea cero en su propio marco de referencia, lo cual es necesario ya que el objeto no puede moverse (ni acelerar) en este fotograma.
La relatividad general dice que la gravedad no es más que una fuerza inercial. Esto fue llamado el principio de equivalencia por Einstein. Ya que la fuerza gravitacional en la Tierra apunta hacia abajo, se deduce que debemos estar acelerando constantemente hacia arriba mientras nos paramos en la superficie de la Tierra. El problema obvio de esta interpretación de la gravedad es que no parece que nos estemos alejando del centro de la Tierra, lo que parecería ser una consecuencia natural de tal aceleración. Sin embargo, la relatividad tiene una sorpresa para nosotros aquí.
De las consideraciones anteriores se desprende que se puede aprender algo sobre la relatividad general examinando las propiedades de los marcos de referencia acelerados. En particular, podemos obtener una idea de la aparente paradoja anterior. La ecuación (6.17) muestra que la velocidad de un objeto sometido a una aceleración intrínseca constante\(a\) (tenga en cuenta que hemos caído el “primo”\(a \) para simplificar la notación) es
\[ dx at v = --- = -----------21∕2, dt [1 + (at∕c) ] \label{6.21} \]
donde\(t \) esta el tiempo y\(c \) es la velocidad de la luz. Una función\(x\) (\(t\)) que satisface la ecuación 6.21} es
\[ 2 2 1∕2 x(t) = (c ∕a)[1 + (at∕c) ] . \label{6.22}\]
(Verifica esto diferenciándolo.) El intervalo OB en la figura 6.6 es de longitud\(x\) (0) =\(c\) 2\(∕A\).
La línea inclinada OA es una línea de simultaneidad asociada con la línea mundial no acelerada tangente a la línea mundial acelerada en el punto A. Esta línea de simultaneidad pasa por el origen, como se muestra en la figura 6.6. Para demostrarlo, multiplique las ecuaciones (6.21) y (6.22) juntas y resuelva para\(v∕c\):
\[v ∕c = ct∕x. \label{6.23}\]
De la figura 6.6 vemos que\(ct∕x \) es la pendiente de la línea OA, donde (\(x,\)\( ct\)) son las coordenadas del evento A. La ecuación (6.23) muestra que esta línea es efectivamente la línea deseada de simultaneidad, ya que su pendiente es la inversa de la pendiente de la línea mundial,\(c∕v\). Como no hay nada de especial en el evento A, inferimos que todas las líneas de simultaneidad asociadas a la línea mundial acelerada pasan por el origen.
Ahora indagamos sobre la longitud del intervalo invariante OA en la figura 6.6. Recordando que\(I\) 2 =\(x\) 2 -\(c\) 2\(t\) 2 y usando la ecuación 6.22}, encontramos que la longitud de OA es
\[ 2 2 2 1∕2 4 2 1∕2 2 I = (x - c t ) = (c ∕a ) = c∕a, \label{6.24}\]
que es la misma que la longitud del intervalo OB. Por extensión, todos los eventos en la línea mundial acelerada son el mismo intervalo invariante desde el origen. Recordando que el intervalo a lo largo de una línea de simultaneidad es la distancia en el marco de referencia asociado, llegamos a la sorprendente conclusión de que aunque el objeto asociado a la línea del mundo curvo en la figura 6.6 se está acelerando alejándose del origen, siempre permanece la misma distancia (en sí misma marco) desde el origen.
La analogía entre este problema y la aparente paradoja en la que uno permanece a una distancia fija del centro de la tierra mientras se acelera alejándose de él no es perfecta. En particular, el caso de la tierra depende de la existencia de la masa terrestre.
Desplazamiento al rojo gravitacional
La luz emitida a un nivel inferior en un campo gravitacional tiene su frecuencia reducida a medida que viaja a un nivel superior. A este fenómeno se le llama el desplazamiento al rojo gravitacional. La Figura 6.26 muestra por qué sucede esto. Dado que experimentar una fuerza gravitacional equivale a estar en un marco de referencia acelerado, podemos utilizar las herramientas de relatividad especial para ver el proceso de emisión y absorción de luz desde el punto de vista del marco no acelerado o inercial. En este marco de referencia el observador de la luz está acelerando hacia la derecha, como lo indica la línea curva del mundo en la figura 6.26, lo que equivale a una fuerza gravitacional hacia la izquierda. La luz es emitida en el punto A con frecuencia\(ω \) por una fuente que está estacionaria en este instante. En este instante el observador también se encuentra estacionario en este marco. Sin embargo, para cuando la luz llega al observador, él o ella tiene una velocidad a la derecha lo que significa que el observador mide una frecuencia desplazada Doppler\(ω\) ′ para la luz. Ya que el observador se está alejando de la fuente,\(ω\) ′\(< ω\), como se indicó anteriormente.
El desplazamiento Doppler relativista viene dado por
\[ ′ ( )1∕2 ω-- 1---U-∕c ω = 1 + U ∕c , \label{6.25} \]
por lo que tenemos que computar\(U∕c\). La línea de simultaneidad para el observador en el punto B pasa por el origen, y es así dada por el segmento de línea OB en la figura 6.26. La pendiente de esta línea es\(U∕c\), donde\(U \) está la velocidad del observador en el punto B. De la figura vemos que esta pendiente también viene dada por la relación\(X\) ′\(∕X\). Equiparando estos, eliminando\(X \) a favor de\(L \) = (\(X\)2 -\(X\) ′ 2) 1 2 =\(c\) 2\(∕g\), que es la distancia invariante real del observador desde el origen, y sustituyendo en la ecuación 6.25} da como resultado nuestra fórmula gravitacional de desplazamiento al rojo:
\[ ′ ( ′)1 ∕2 ( 2 ′21∕2 ′)1∕2 ω--= X----X-- = (L--+-X---)-----X-- . ω X + X ′ (L2 + X ′2)1∕2 + X ′ \label{6.26} \]
Si\(X\) ′ = 0, entonces no hay corrimiento al rojo, porque la fuente se coloca con el observador. Por otro lado, si la fuente se encuentra en el origen, entonces\(X\) ′ =\(X\), la frecuencia desplazada Doppler es cero. Además, la luz nunca llega al observador, ya que la línea del mundo es asintótica a la línea del mundo de la luz que pasa por el origen. Si la fuente se encuentra en un nivel superior en el campo gravitacional que el observador, de manera que\(X\) ′\(< \) 0, entonces la frecuencia se desplaza a un valor mayor, es decir, se convierte en un “desplazamiento azul”.
La ecuación (6.26) funciona para geometrías más complejas que las asociadas con un marco de referencia acelerado, por ejemplo, para el campo gravitacional\(g \) asociado a una estrella, siempre y cuando |\(X\)\(c\) ′|2\(∕g\). En este caso ya no\(L \) es la distancia al centro de la estrella sino que se mantiene igual a\(c\) 2\(∕g\).
Horizontes de eventos
La línea diagonal de 45° que pasa por el origen en la figura 6.6 se denomina horizonte de eventos para el observador acelerado en esta figura. Observe que la luz de la “zona crepuscular” arriba y hacia la izquierda del horizonte de eventos no puede llegar al observador acelerado. Sin embargo, lo contrario no es cierto: una señal luminosa emitida a la izquierda por el observador puede cruzar el horizonte de eventos hacia la “zona crepuscular”. El horizonte de eventos tiene así un peculiar carácter unidireccional: pasa señales de derecha a izquierda, pero no de izquierda a derecha.
Problemas
- Un objeto se mueve como se describe en la figura 6.8, que muestra su posición\(x \) en función del tiempo\(t\).
- ¿La velocidad es positiva, negativa o cero en cada uno de los puntos A, B, C, D, E y F?
- ¿La aceleración es positiva, negativa o cero en cada uno de los puntos A, B, C, D, E y F?
Figura 6.8: Posición de un objeto en función del tiempo.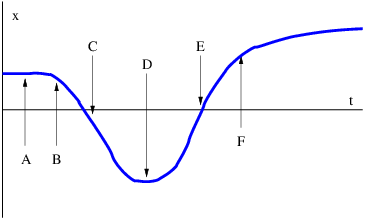
_____________________________________
- Un objeto se mueve en sentido antihorario a velocidad constante alrededor del círculo mostrado en la figura 6.9 debido a que está unido por una cuerda al centro del círculo en el punto O.
- Dibuje los vectores de velocidad del objeto en los puntos A, B y C.
- Esboce los vectores de aceleración del objeto en los puntos A, B y C.
- Si la cadena se rompe en el punto A, dibuje la trayectoria posterior seguida por el objeto.
Figura 6.9: Objeto en movimiento circular.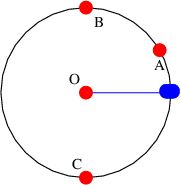
_____________________________________
- Qué tan rápido vas después de acelerar desde el reposo con aceleración intrínseca\(a \) = 10 m s - 2 después de los tiempos dados medidos en el fotograma de descanso:
- 10 y?
- ¿100000 y?
Exprese su respuesta como la velocidad de la luz menos su velocidad real. Pista: Es posible que tengas un problema numérico en la segunda parte, que deberías intentar resolver usando la aproximación (1 +\(ϵ\)) x ≈ 1 +\(xϵ\), que es válida para |\(ϵ\) |1.
- La línea mundial de un objeto se define por\(x\) (\(t\)) = (\(d\)\(c\)2 +\(t\) 2 2) 1 2 donde\(d \) es una constante y\(c \) es la velocidad de la luz.
- Encuentra la velocidad del objeto en función del tiempo.
- Usando el resultado anterior, encuentra la pendiente de la tangente a la línea del mundo en función del tiempo.
- Encuentra donde la línea de simultaneidad correspondiente a cada línea tangente mundial cruza el\(x \) eje.
- Un automóvil acelera en\(x \) sentido positivo a 3 m s - 2.
- ¿Cuál es la fuerza neta sobre un hombre de 100 kg en el automóvil visto desde un marco de referencia inercial?
- ¿Cuál es la fuerza inercial que experimenta este hombre en el marco de referencia del automóvil?
- ¿Cuál es la fuerza neta que experimenta el hombre en el marco de referencia (acelerado) del automóvil?
- Una persona se encuentra sentada en una cómoda silla en su casa de Bogotá, Colombia, que se encuentra esencialmente en el ecuador.
- ¿Cuál tendría que ser el periodo rotacional de la tierra para que esta persona sea ingrávida?
- ¿Cuál es su aceleración según el principio de equivalencia en el marco terrestre en esta situación?
- En el tiempo\(t \) = 0 un Zork (una criatura del planeta Zorkheim) acelerando hacia la derecha a\(a \) = 10 3 m s - 2 en una nave espacial cae accidentemente su cronómetro de la nave espacial justo cuando su velocidad es cero.
- Describa cualitativamente cómo las manecillas del reloj parecen moverse hacia el Zork mientras observa el reloj a través de un potente telescopio.
- Después de mucho tiempo ¿qué lee el reloj?
Pista: Dibuja un diagrama espacio-tiempo con las líneas mundiales de la nave espacial y el reloj. Después envía los rayos de luz del reloj a la nave espacial.
- Usando un diagrama espacio-tiempo, muestra por qué las señales de eventos en el lado oculto del horizonte de eventos de una nave espacial acelerada no pueden llegar a la nave espacial.
- Ecuación aproximada 6.26} a primer orden en\(X\) ′ para el caso en el que\(X\) \(L\)′.
- }
- Imagínese dos relojes idénticos, uno encima del volcán Chimborazo en Ecuador (6300 m sobre el nivel del mar), el otro en la ciudad ecuatoriana de Guayaquil (a nivel del mar).
- Desde la perspectiva del Chimborazo, ¿el reloj en Guayaquil parece estar funcionando más rápido o más lento que el reloj Chimborazo? Explique.
- Calcular la diferencia de frecuencia fraccional (\(ω \)-\(ω\) ′)\(∕ω \) en este caso, donde\(ω \) está la frecuencia del reloj de Guayaquil como se observa en Guayaquil (y la frecuencia del reloj Chimborazo en Chimborazo) y\(ω\) ′ es la frecuencia del reloj Guayaquil observada desde Chimborazo. Es posible que desee utilizar los resultados del problema anterior.
Capítulo 7 Olas de la materia
Comenzamos nuestro estudio de la mecánica cuántica discutiendo la difracción que experimentan los rayos X y los electrones cuando interactúan con un cristal. Los rayos X son una forma de radiación electromagnética con longitudes de onda comparables a las distancias entre átomos. La dispersión de los átomos en una estructura cristalina regular da como resultado un patrón de interferencia que es en muchos aspectos similar al patrón de una rejilla de difracción. Primero desarrollamos la ley de Bragg para la difracción de rayos X de un cristal. Luego se describen dos técnicas prácticas para hacer difracción de rayos X.
Resulta que los electrones tienen propiedades onduladas y también sufren difracción de Bragg por cristales. La difracción de Bragg proporciona así un puente crucial entre los mundos de las ondas y las partículas. Con este puente introducimos las ideas clásicas de impulso y energía relacionándolas con el vector de onda y la frecuencia de una onda. Las propiedades de las olas también dan origen al principio de incertidumbre de Heisenberg.
En el cuadro 7.1 se muestra una tabla de los premios Nobel asociados a las ideas presentadas en este capítulo. Esto nos da una idea de la cronología de estos descubrimientos e indica lo importantes que fueron para el desarrollo de la física a principios del siglo XX.
Ley de Bragg
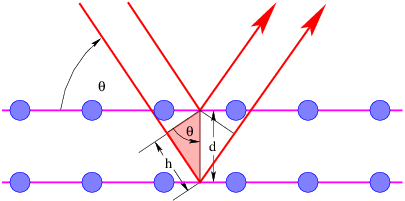
La Figura 7.1 ilustra esquemáticamente la interferencia entre ondas que se dispersan de dos filas adyacentes de átomos en un cristal. El efecto neto de la dispersión de una sola fila es equivalente a la reflexión parcial de un espejo imaginado para estar alineado con la fila. Así, el ángulo de “reflexión” es igual al ángulo de incidencia para cada fila. Entonces se produce interferencia entre los haces reflejándose en diferentes filas de átomos en el cristal.
Para las dos filas adyacentes que se muestran en la figura 7.1, la diferencia de trayectoria entre vigas es de 2\(h \) = 2\(d\) sin\(θ\). Para la interferencia constructiva esto debe ser un número entero de longitudes de onda,\(mλ\), donde el entero\(m \) se llama el orden de interferencia. El resultado es la ley de difracción de Bragg:
\[m λ = 2dsinθ, m = 1,2,3 ... (Bragg ’s law). \label{7.1}\]
Si solo se involucran dos filas, la transición de la interferencia constructiva a la destructiva como\(θ \) cambios es gradual. Sin embargo, si se produce interferencia de muchas filas, entonces los picos de interferencia constructiva se vuelven muy agudos con interferencia principalmente destructiva en el medio. Esta agudización de los picos a medida que aumenta el número de filas es muy similar a la nitidez de los picos de difracción de una rejilla de difracción a medida que aumenta el número de ranuras.
Técnicas de difracción de rayos
En los experimentos de difracción de Bragg se utilizan dos tipos de dianas: monocristales y dianas en polvo.
Cristal único
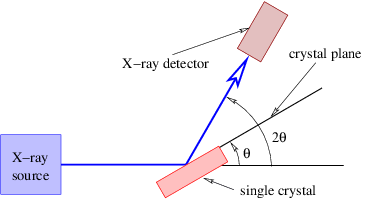
En una configuración de cristal único, se monta un detector de rayos X como se muestra en la figura 7.2. Un dispositivo mecánico mantiene el detector orientado de manera que el ángulo de incidencia sea igual al ángulo de reflexión para el plano cristalino deseado. Se buscan picos en la tasa de detección de rayos X a medida que\(θ \) se varía el ángulo.
La ventaja de este tipo de aparatos es que se observan picos de difracción solo del plano cristalino seleccionado.
Objetivo en Polvo
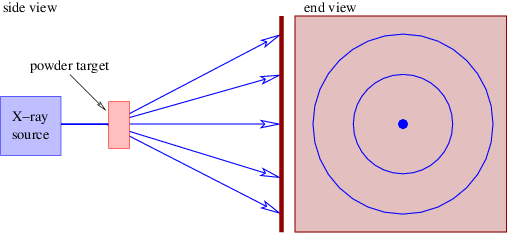
El polvo en un blanco de polvo es realmente un conglomerado de muchos cristales diminutos orientados aleatoriamente. Así, para cada posible ángulo de difracción de Bragg hay cristales orientados correctamente para que se lleve a cabo la difracción de Bragg. El detector suele ser una placa fotográfica o un dispositivo electrónico equivalente como se ilustra en la figura 7.3. Por cada ángulo de difracción de Bragg se ve un anillo en la placa concéntrico con el eje del haz de rayos X incidente.
La ventaja de este tipo de sistemas es que no se necesita conocimiento de las orientaciones del plano cristalino. Además, no se requiere un solo cristal grande. Sin embargo, todos los posibles ángulos de dispersión de Bragg se ven a la vez, lo que puede generar confusión en la interpretación de los resultados.
Significado de la función de onda cuántica
La difracción de Bragg ilustra lo más difícil de entender sobre la mecánica cuántica, a saber, que las partículas pueden tener propiedades onduladas y las ondas pueden tener propiedades similares a las partículas.
La variación de la intensidad de rayos X con el ángulo visto en un aparato de difracción de Bragg es muy difícil de explicar en otros términos distintos de la interferencia de onda. Sin embargo, los rayos X son detectados típicamente por un dispositivo como un contador Geiger que produce un pulso de electricidad por cada partícula de rayos X, o fotón, que la golpea. Así, los rayos X a veces actúan como partículas y a veces como ondas.
La luz no es la única en tener propiedades tanto de partículas como de onda. Davisson y Germer y más tarde G. P. Thomson (hijo de J. J. Thomson, el descubridor del electrón) demostraron que los electrones también pueden actuar como ondas. Lo hicieron demostrando que los electrones experimentan difracción de Bragg en cristales, tanto como lo hacen los rayos X.
La mayoría de los físicos (incluido Albert Einstein) han encontrado que la mecánica cuántica es extremadamente extraña, así que si sientes lo mismo, ¡estás en buena compañía! Sin embargo, existe una interpretación útil de la mecánica cuántica que al menos nos permite continuar con su uso para resolver problemas, aunque no satisfaga nuestras reservas intuitivas sobre la teoría.
El desplazamiento de la onda de materia asociada a una partícula se suele llamar la función de onda,\(ψ\). No está del todo claro de qué\(ψ \) es un desplazamiento, pero su uso es sencillo. El cuadrado absoluto de la función de onda, |\(ψ\) (\(x,t\)) | 2, es proporcional a la probabilidad de encontrar la partícula asociada en posición\(x \) y tiempo\(t\). El cuadrado absoluto se toma porque bajo muchas circunstancias la función de onda es realmente compleja, es decir, tiene partes tanto reales como imaginarias. Las razones de esto se discutirán más adelante.
Debido a la interpretación de la función de onda, la mecánica cuántica es una teoría probabilística. No nos dice con certeza qué le sucede a una partícula en particular. En cambio, nos dice la probabilidad de detectar la partícula en cualquier ubicación dada. Si se realizan muchos experimentos, con una partícula por experimento, los números de experimentos con partículas que se detectan en las diversas ubicaciones posibles son proporcionales a las probabilidades mecánicas cuánticas.
7.4 Sentido y Tonterías en
Mecánica Cuántica
El misterio esencial de la mecánica cuántica se vuelve más claro cuando se discute en el contexto conceptualmente más simple de la interferencia de dos rendijas. Si la luz y los electrones pueden tener propiedades tanto de partículas como de onda, entonces uno podría preguntarse a través de cuál de las dos rendijas pasó la partícula. Sin embargo, en física una pregunta simplemente no tiene sentido si no puede ser respondida por experimento.
De hecho, se puede realizar un experimento para determinar qué hendidura pasa el fotón o electrón de rayos X en el experimento de dos hendiduras. Sin embargo, por el acto mismo de hacer esta medición, se altera la forma de la onda asociada. En particular, dado que el cuadrado absoluto del desplazamiento de onda representa la probabilidad de encontrar la partícula, una vez que la partícula se ha encontrado definitivamente pasando por una u otra de las rendijas, la función de onda colapsa en un paquete de onda muy pequeño ubicado en la posición observada del partícula. Así, el desplazamiento de onda se convierte en cero en la hendidura por la que no pasó. Sin embargo, el patrón de interferencia resulta de la superposición de ondas que emanan de dos hendiduras. Si ninguna onda viene de una de las hendiduras (porque el desplazamiento de onda es cero allí), ¡entonces no puede haber patrón de interferencia!
Ahora podemos hacer el argumento inverso. Si hay un patrón de interferencia, entonces sabemos que el desplazamiento de onda no es cero en ambas hendiduras. A partir de la interpretación probabilística del desplazamiento de onda, concluimos que no podemos decir, ni siquiera en principio, por qué hendidura pasó la partícula. No es sólo que no sepamos la respuesta a esta pregunta; simplemente no hay ningún experimento que nos pueda dar una respuesta sin destruir el patrón de interferencia. En otras palabras, la pregunta “¿Por qué hendidura pasó la partícula?” es una pregunta sin sentido en el caso en que realmente se produce un patrón de interferencia.
El físico estadounidense Richard Feynman notó que el comportamiento anterior puede interpretarse como una violación de las leyes normales de probabilidad. Estas leyes dicen que la probabilidad de un evento es la suma de las probabilidades de formas alternas independientes para que ese evento ocurra. Por ejemplo, la probabilidad de que una partícula alcance el punto A en la pantalla de detección de una configuración de dos rendijas es solo la probabilidad\(P\) 1 de que la partícula alcance el punto A después de pasar por la hendidura 1, más la probabilidad\(P\) 2 para la partícula para alcanzar el punto A después de pasar por la hendidura 2. Por lo tanto, si\(P\) 1 =\(P\) 2 = 0\(.\) 1, entonces la probabilidad de que la partícula alcance el punto A independientemente de la hendidura por la que pasó debería ser\(P\) total =\(P\) 1 +\(P\) 2 = 0\(.\) 2. No obstante, si el punto A resulta ser un punto de interferencia destructiva, entonces sabemos que\(P\) total = 0.
Feynman propuso que la regla anterior que establece que se suman probabilidades independientes alternas, es simplemente incorrecta. En su lugar Feynman aseveró que las amplitudes de probabilidad suman en su lugar, donde la amplitud de probabilidad en este caso es solo la función de onda asociada a la partícula. La probabilidad total para un proceso se obtiene sumando las amplitudes de probabilidad alternas y tomando el cuadrado absoluto de la suma.
La visión de Feynman es una expresión particularmente compacta de la llamada interpretación de Copenhague de la mecánica cuántica que evolucionó a partir de las ideas de Niels Bohr, Werner Heisenberg, Max Born y otros en la década de 1920. Prescinde de la dualidad onda-partícula y otro bagaje filosófico al decir “Las partículas son reales en el sentido de que las podemos observar, pero la única teoría que tenemos es sobre las amplitudes de probabilidad para las partículas”. Esta interpretación de la mecánica cuántica puede ser extraña, pero parece ser autoconsistente y de acuerdo con el experimento.
Masa, Momentum y Energía
En esta sección relacionamos las ideas clásicas de masa, impulso y energía con lo que hemos hecho hasta ahora. Históricamente, estas conexiones fueron hechas por primera vez por Max Planck y Louis de Broglie con la ayuda de Albert Einstein. Se invoca la difracción de electrones de Bragg como prueba experimental de las relaciones Planck y de Broglie.
Técnicamente, no necesitamos las ideas de masa, impulso y energía para hacer física; las nociones de número de onda, frecuencia y velocidad de grupo son suficientes para describir y explicar todos los fenómenos observados. Sin embargo, la masa, el impulso y la energía están tan firmemente incrustados en la física que ¡uno no podría hablar con otros físicos sin comprender estas cantidades!
Planck, Einstein y de Broglie
Max Planck fue el primero en desarrollar una teoría explicando la densidad energética de la radiación electromagnética en una caja a una temperatura fija. Albert Einstein extendió las ideas de Planck postulando que la energía de la radiación electromagnética se cuantifica en trozos llamados fotones. La energía\(E \) de un fotón se relaciona con la frecuencia de la radiación electromagnética por la ecuación
\[E = hf = ¯hω (Planck-Einstein relation), \label{7.2}\]
donde\(f \) es la frecuencia rotacional de la onda electromagnética asociada y\(ω\) es su frecuencia angular. La constante\(h \) = 6\(.\) 63 × 10 - 34 kg m 2 s - 1 se llama constante de Planck. La constante relacionada\(ℏ\) =\(h∕\) 2\(π \) = 1\(.\) 06 × 10 - 34 kg m 2 s - 1 también se conoce como constante de Planck, pero para evitar confusiones con la constante original, generalmente nos referiremos a ella como “h bar”.
Observe que ha aparecido una nueva dimensión física, a saber, la masa, con el kilogramo unitario, abreviado “kg”. El significado físico de la masa es muy parecido a nuestra comprensión intuitiva del concepto, es decir, como una medida de la resistencia de un objeto a que se cambie su velocidad. El significado científico preciso surgirá en breve.
Einstein demostró que la idea de Planck podría ser utilizada para explicar la emisión de electrones que ocurre cuando la luz incide en la superficie de un metal. Esta emisión, que se denomina efecto fotoeléctrico, sólo puede ocurrir cuando se suministran electrones con cierta energía mínima\(E\) B requerida para desprenderlos del metal. El experimento muestra que esta emisión se produce sólo cuando la frecuencia de la luz excede un cierto valor mínimo. Este valor resulta igual a\(ω\) min =\(E\) B\(∕\)\(ℏ\), lo que sugiere que los electrones ganan energía al absorber un solo fotón. Si la energía fotónica,\(ℏ\)\(ω\), excede de\(E\) B, entonces se emiten electrones, de lo contrario no lo son. Es mucho más difícil explicar el efecto fotoeléctrico a partir de la teoría clásica de la luz. El valor de\(E\) B, llamado energía de unión o función de trabajo, es diferente para diferentes metales.
Louis de Broglie propuso que la relación energía-frecuencia de Planck se extendiera a todo tipo de partículas. Además planteó la hipótesis de que el impulso\(Π\) de la partícula y el vector\(k\) de onda de la onda correspondiente estaban relacionados de manera similar:
\[Π = ¯hk (de Broglie relation). \label{7.3}\]
Tenga en cuenta que esto también se puede escribir en forma escalar en términos de la longitud de onda como π =\(h∕λ\). (Usamos\(Π\) en lugar de lo más común\(p\) para el impulso, porque como veremos, hay dos tipos diferentes de impulso, uno relacionado con el número de onda, el otro relacionado con la velocidad de una partícula. En muchos casos son iguales, pero hay ciertas situaciones importantes en las que no lo son.)
La hipótesis de De Broglie se inspiró en el hecho de que la frecuencia de onda y el número de onda son componentes del mismo cuatro vectores según la teoría de la relatividad, y por lo tanto están estrechamente relacionados entre sí. Así, si la energía de una partícula está relacionada con la frecuencia de la onda correspondiente, entonces debería haber alguna cantidad similar que esté relacionada correspondientemente con el número de onda. Resulta que el impulso es la cantidad apropiada. El significado físico del impulso se aclarará a medida que avancemos.
También encontraremos que la frecuencia de reposo,\(μ\), de una partícula está relacionada con su masa,\(m\):
\[ 2 Erest ≡ mc = ¯hμ. \label{7.4}\]
La cantidad\(E\) resto se llama energía de reposo de la partícula.
Desde nuestra perspectiva, la energía, el impulso y la energía de descanso son solo versiones escaladas de frecuencia, vector de onda y frecuencia de reposo, con un factor de escala\(ℏ\). Por lo tanto, podemos definir un cuatro-momento como una versión escalada de la onda de cuatro vectores:
\[Π-= ¯hk. \label{7.5}\]
El componente espacial de π es justo\(Π\), mientras que la parte similar al tiempo lo es\(E∕c\).
Planck, Einstein y de Broglie tenían amplios antecedentes en la mecánica clásica, en la que los conceptos de energía, impulso y masa tienen un significado preciso. En este texto no presuponemos tal trasfondo. Quizás la mejor estrategia en este punto es pensar en estas cantidades como versiones escaladas de frecuencia, número de onda y frecuencia de reposo, donde está el factor de escala\(ℏ\). El significado de estas cantidades para la mecánica clásica surgirá poco a poco.
Cantidades de partículas
Ahora recapitulemos lo que sabemos sobre las ondas relativistas, y cómo este conocimiento se traduce en conocimiento sobre la masa, la energía y el impulso de las partículas. En las siguientes ecuaciones, la forma de la izquierda se expresa en términos de onda, es decir, en términos de frecuencia, número de onda y frecuencia de reposo. La forma de la derecha es la ecuación idéntica expresada en términos de energía, impulso y masa. Dado que estas últimas variables son solo formas escaladas de las primeras, las dos formas de cada ecuación son equivalentes.
Comenzamos con la relación de dispersión para las ondas relativistas:
\[ 2 2 2 2 2 2 2 2 4 ω = k c + μ E = Π c + m c . \label{7.6}\]
Cálculo de la velocidad del grupo,\(u\) g =\(dω∕dk\), a partir de los rendimientos de relación de dispersión
\[ 2 2 ug = c-k- ug = c-Π-. ω E \label{7.7} \]
Estos dos conjuntos de ecuaciones representan lo que sabemos sobre las ondas relativistas, y lo que este conocimiento nos dice sobre las relaciones entre la masa, la energía y el impulso de las partículas relativistas. En caso de duda, refiérase de nuevo a estas ecuaciones, ya que funcionan en todos los casos, ¡incluso para partículas con masa cero!
Es útil dar vuelta a las ecuaciones (7.6) y (7.7) para expresar la frecuencia en función de la frecuencia de reposo y la velocidad de grupo,
\[ ------μ------- -----mc2------ ω = (1 - u2∕c2)1∕2 E = (1 - u2∕c2)1∕2, g g \label{7.8} \]
y el número de onda como una función similar de estas cantidades:
\[ ---μug-∕c2---- -----mug------ k = (1 - u2∕c2)1∕2 Π = (1 - u2∕c2)1∕2. g g \label{7.9} \]
¡Tenga en cuenta que las ecuaciones (7.8) y (7.9) funcionan solo para partículas con masa distinta de cero! Para las partículas de masa cero tanto los numeradores como los denominadores de las ecuaciones (7.8) y (7.9) son cero, haciendo que estas ecuaciones sean indefinidas, y es necesario usar las ecuaciones (7.6) y (7.7) con\(m \) = 0 y\(μ \) = 0 en su lugar.
La cantidad\(ω \) -\(μ \) indica cuánto la frecuencia excede la frecuencia de reposo. Observe que si\(ω \) =\(μ\), entonces de la ecuación 7.6}\(k \) = 0. Así, los valores positivos de\(ω\) k ≡\(ω \) -\(μ \) indican |\(k\) |\(> \) 0, lo que significa que la partícula se mueve según la ecuación (7.7). Llamemos a\(ω\) k la frecuencia cinética:
\[ [ ] [ ] -------1------ ------1------- 2 ωk = (1 - u2∕c2)1∕2 - 1 μ K = (1 - u2∕c2)1∕2 - 1 mc . g g \label{7.10} \]
Llamamos a\(K \) la energía cinética por razones similares. Nuevamente, la ecuación 7.10} solo funciona para partículas con masa distinta de cero. Para partículas de masa cero, la energía cinética es igual a la energía total.
Obsérvese que los resultados de esta sección son válidos únicamente para partículas libres, es decir, partículas a las que no se aplica fuerza alguna. La fuerza en la mecánica clásica y cuántica se trata en el siguiente capítulo.
Límites no relativistas
Cuando la masa es distinta de cero y la velocidad de grupo es mucho menor que la velocidad de la luz, es útil calcular formas aproximadas de las ecuaciones anteriores válidas en este límite. Usando la aproximación (1 +\(ϵ\)) x ≈ 1 +\(xϵ\), encontramos que la relación de dispersión se vuelve
\[ 2 2 2 ω = μ + k-c-- E = mc2 + Π---, 2 μ 2m \label{7.11} \]
y la ecuación de velocidad de grupo toma la forma aproximada
\[ c2k Π ug = ---- ug = --. μ m \label{7.12} \]
Los límites no relativistas para las ecuaciones (7.8) y (7.9) se convierten en
\[ μu2g mu2g ω = μ + --2- E = mc2 + ----- 2c 2 \label{7.13} \]
y
\[ 2 k = μug ∕c Π = mug, \label{7.14}\]
mientras que la ecuación de energía cinética aproximada es
\[ μu2 mu2 ωk = --2g K = ---g. 2c 2 \label{7.15} \]
Solo un recordatorio — ¡las ecuaciones de esta sección no son válidas para partículas sin masa!
Prueba Experimental
¿Cómo podemos probar las predicciones anteriores contra el experimento? El punto clave es poder relacionar los aspectos de onda con los aspectos de partícula de una onda-partícula mecánica cuántica. La ecuación (7.9), o ecuación 7.14} en el caso no relativista, relaciona el número de onda de una partícula\(k \) con su velocidad\(u\) g. Ambas cantidades se pueden medir en un experimento de la ley de Bragg con electrones. En este experimento los electrones se disparan a un cristal con dimensiones atómicas conocidas a una velocidad conocida, que identificamos con la velocidad del grupo\(u\) g. El ángulo de Bragg que produce interferencia constructiva se puede utilizar para calcular la longitud de onda de la onda electrónica correspondiente y, por lo tanto, el número de onda y el momento. Si el momento se grafica contra la velocidad del grupo en el caso no relativista, se debe encontrar una línea recta, cuya pendiente es la masa de la partícula. En el caso completamente relativista se necesita trazar impulso versus\(u\) g\(∕\) (1 -\(u\) g\(∕c\) 2 2) 1 2 . Nuevamente, una línea recta indica concordancia con la teoría y la pendiente de la línea es la masa de la partícula. Este experimento en particular es difícil de hacer, pero las teorías correspondientes lo verifican en muchos otros experimentos.
Principio de incertidumbre de Heisenberg
Clásicamente, consideramos que la ubicación de una partícula es una pieza de información conocible. En mecánica cuántica la posición de una partícula es bien conocida si el paquete de onda que la representa es de tamaño pequeño. Sin embargo, la mecánica cuántica impone un precio al conocer con precisión la posición de una partícula en términos de la previsibilidad futura de su posición. Esto se debe a que un paquete de ondas pequeñas, que corresponde a un conocimiento preciso de la posición de la partícula correspondiente, implica la superposición de ondas planas correspondientes a una amplia distribución de números de onda. Esto se traduce en una gran incertidumbre en el número de onda, y de ahí el impulso de la partícula. En contraste, un paquete de onda ancha corresponde a una distribución más estrecha de números de onda, y correspondientemente menos incertidumbre en el momento.
Refiriéndose de nuevo a los capítulos 1 y 2, recordemos que tanto las dimensiones longitudinal (a lo largo de la dirección del movimiento) como transversal (normal a la dirección del movimiento) de un paquete de ondas, Δ\(x\) L y Δ\(x\) T, pueden estar relacionadas con la propagación de números de onda longitudinales y transversales, Δ\(k\) L y Δ\(k\) T:
\[ΔkL ΔxL ≈ 1, \label{7.17}\]
Hemos omitido constantes numéricas que son de unidad de orden en estas relaciones aproximadas para mostrar su similitud esencial.
Las ecuaciones anteriores se pueden interpretar de la siguiente manera. Dado que el cuadrado absoluto de la función de onda representa la probabilidad de encontrar una partícula, Δ\(x\) L y Δ\(x\) T representan la incertidumbre en la posición de la partícula. De manera similar, Δ\(k\) L y Δ\(k\) T representan la incertidumbre en los componentes del vector de onda longitudinal y transversal de la partícula. Esta última incertidumbre conduce a la incertidumbre en el movimiento futuro de la partícula:\(k\) los resultados longitudinales más grandes o menores respectivamente en una velocidad de partícula mayor o menor, mientras que la incertidumbre en el número de onda transversal da como resultado incertidumbre en la dirección del movimiento de la partícula. Así, las incertidumbres en cualquier componente de\(k\) resultan en incertidumbres en el componente correspondiente de la velocidad de la partícula, y por lo tanto en su posición futura.
Las ecuaciones (7.16) y (7.17) muestran que la incertidumbre en las posiciones presente y futura de una partícula son complementarias. Si la posición actual se conoce con precisión debido al pequeño tamaño del paquete de ondas asociado, entonces la posición futura no es muy predecible, porque el paquete de ondas se dispersa rápidamente. Por otro lado, un paquete de onda inicial a gran escala significa que la posición actual es poco conocida, pero la incertidumbre en la posición, pobre como es, no aumenta rápidamente con el tiempo, ya que el paquete de ondas tiene una pequeña incertidumbre en el vector de onda y así se dispersa lentamente. Esta es una declaración del principio de incertidumbre de Heisenberg.
El principio de incertidumbre también se aplica entre la frecuencia y el tiempo:
\[Δω Δt ≈ 1. \label{7.18}\]
Esto se manifiesta en la ecuación de frecuencia de\(∕T\) latido 1 latido = Δ\(f \) = Δ\(ω∕\) 2\(π\). El latido del periodo\(T\) beat puede ser considerado como el tamaño de un “paquete de onda en el tiempo”. La ecuación de frecuencia de latido puede reescribirse como Δ\(ωT\) latido = 2\(π\), que es lo mismo que la ecuación (7.18) si\(π \) se ignora el factor de 2 y el\(T\) latido se identifica con Δ\(t\).
Las formas anteriores del principio de incertidumbre no son relativisticamente invariantes. Se puede obtener una forma invariante útil transformándose en el sistema de coordenadas en el que una partícula es estacionaria. En este marco de referencia el tiempo\(t\) se convierte en el tiempo adecuado\(τ \) asociado a la partícula. Además, la frecuencia\(ω \) se convierte en la frecuencia de reposo\(μ\). El principio de incertidumbre se convierte así
\[Δ μΔ τ ≈ 1 \label{7.19}\]
en este marco de referencia. Sin embargo, dado que Δ\(μ \) y Δ\(τ \) son invariantes relativistas, esta expresión del principio de incertidumbre es válida en cualquier marco de referencia.
Es más común expresar el principio de incertidumbre en términos de masa, impulso y energía multiplicando las ecuaciones (7.16) - (7.19) por\(ℏ\). Agrupando las ecuaciones de impulso, encontramos
\[Δ Π Δx ≈ ¯h, \label{7.21}\]
y
\[Δ (mc2 )Δ τ ≈ ¯h. \label{7.22}\]
La mecánica clásica es el reino de la mecánica cuántica en la que las dimensiones del sistema de interés son mucho mayores que las longitudes de onda de las ondas correspondientes a las partículas que constituyen el sistema. En este caso las incertidumbres inducidas por el principio de incertidumbre no son importantes. Este límite es análogo al límite de óptica geométrica para la luz. Así, podemos decir que la mecánica clásica es el límite de la óptica geométrica de la mecánica cuántica.
Problemas
- Un electrón con longitud de onda\(λ \) = 1\(.\) 2 × 10 - 10 m se somete a difracción de Bragg a partir de un solo cristal con espaciamiento plano atómico de\(d \) = 2 × 10 - 10 m.
- Calcula los ángulos de Bragg (¡todos ellos!) para lo cual se produce una interferencia constructiva.
- Calcular la velocidad del electrón.
- Supongamos que los electrones inciden en dos hendiduras en una placa, lo que resulta en un patrón de difracción de dos hendiduras en una pantalla en el otro lado de la placa. La probabilidad de que un electrón pase por cualquiera de las hendiduras y alcance el punto A en la pantalla es\(P\), asumiendo que la otra hendidura está bloqueada.
- Si hay dos hendiduras abiertas y A es un punto de interferencia constructiva, ¿cuál es la probabilidad de que un electrón llegue a A? Pista: Recuerda que las amplitudes, no las probabilidades agregan.
- Si hay dos hendiduras abiertas y A es un punto de interferencia destructiva, ¿cuál es la probabilidad de que un electrón llegue a A?
- Si hay dos hendiduras abiertas, ¿cuál es la probabilidad de que un electrón alcance el punto A de acuerdo con la regla convencional que suman probabilidades? (Este es el resultado que uno esperaría si, por ejemplo, las partículas fueran balas de ametralladora y las hendiduras estuvieran, digamos, a 5 cm de distancia).
- Si la separación de rendijas es mucho mayor que la longitud de onda de los electrones, ¿cómo afecta esto al espaciamiento de las regiones de interferencia constructiva y destructiva? Explicar cómo los resultados de las partes (a) y (b) llegan a ser aproximadamente consistentes con los de la parte (c) en este caso.
- Calcular la frecuencia de reposo (angular) de un electrón y un neutrón. (Busque sus masas.)
- ¿Cómo se simplifica la relación de dispersión para las ondas relativistas si la frecuencia de reposo (y por lo tanto la masa de partículas) es cero? ¿Cuál es la velocidad del grupo en este caso?
- Los rayos X son fotones con frecuencias alrededor de 2000 veces las frecuencias de los fotones de luz ordinarios. A partir de esta información y de lo que se sabe de la luz, inferir la velocidad aproximada de los electrones que tienen propiedades de difracción de Bragg similares a los rayos X. ¿Los electrones son relativistas o no relativistas?
- Los electrones con velocidad\(v \) = 0\(.\) 6\(c \) se difractan con un medio ángulo de difracción de 0\(.\) 2 radianes cuando chocan contra un objeto. ¿Cuál es el tamaño aproximado del objeto? Pista: La difracción de una onda por un objeto de cierto tamaño es bastante similar a la difracción por un agujero en una pantalla del mismo tamaño.
- Elaborar una fórmula aproximada para la energía cinética de una partícula en función de la masa\(m \) y la velocidad\(u\) g la cual es válida cuando\(u\) g 2\(c\) 2. Pista: Utilice la aproximación (1 +\(ϵ\)) x ≈ 1 +\(xϵ\), que es válida para |\(ϵ\) |1. A medida que\(u\) g\(∕c\) se hace más grande, ¿cómo se desvía esta fórmula aproximada de la fórmula exacta?
- Elaborar una fórmula aproximada para el impulso de una partícula en función de\(m \) y\(u\) g en el caso donde\(u\) g 2\(c\) 2. Es posible que desee utilizar la aproximación mencionada en el problema anterior.
- Si un fotón se localiza dentro de una distancia Δ\(x\), ¿cuál es la incertidumbre en la energía fotónica?
- Si un electrón se localiza dentro de una distancia Δ\(x\), ¿cuál es la incertidumbre en la energía cinética del electrón? Pista: Siempre y cuando Δπ π, Δπ 2 ≈ 2πΔπ. Para ver por qué, computar\(d\) π 2\(∕d\) π.
- Un tendero arroja algunos frijoles pintos en una báscula, estima su masa como 2 kg, y luego los arroja después de 5 s. ¿Cuál es la incertidumbre mecánica cuántica en esta medición? Supongamos que esto ocurre en Quantum World donde la velocidad de la luz es de 10 m s - 1 (velocidad de un buggy rápido) y la constante de Planck\(ℏ\) = 1 kg m 2 s - 1.
- El texto de física de Mary (masa 0\(.\) 3 kg) tiene que mantenerse con correa (longitud 0\(.\) 5 m) para evitar que se aleje de ella en Quantum World (\(ℏ\)= 1 kg m 2 s - 1).
- Si la correa se rompe repentinamente, ¿cuál es la velocidad máxima a la que es probable que el libro se aleje de su ubicación inicial?
- Para reducir esta velocidad, ¿debería María hacer que la nueva correa sea más corta o más larga que la anterior? Explique.
- Un protón (masa\(M \) = 1\(.\) 7 × 10 - 27 kg) está confinado a un núcleo atómico de diámetro\(D \) = 2 × 10 - 15 m.
- ¿Cuál es la incertidumbre en el impulso del protón?
- Más o menos, ¿qué energía cinética podría esperar que tenga el protón?
La constante de Planck es\(ℏ\) = 1\(.\) 06 × 10 - 34 kg m 2 s - 1. Se puede usar la ecuación no relativista para la energía.
}
Capítulo 8 Óptica geométrica y leyes de Newton
La pregunta que nos motiva a estudiar física es “¿Qué hace que las cosas salgan?” Las respuestas que concebimos a esta pregunta constituyen el tema de la dinámica. Esto contrasta con la pregunta que hemos abordado principalmente hasta ahora, a saber, “¿Cómo van las cosas?” Esta última pregunta es sobre la cinemática. Se necesita una amplia preparación en la cinemática de ondas y partículas en el espacio-tiempo relativista para abordar inteligentemente la dinámica. Esta preparación ya está completa.
En este capítulo describimos tres principios dinámicos diferentes basados respectivamente en el pensamiento mecánico pre-newtoniano, newtoniano y cuántico. Primero discutimos la mecánica newtoniana de las fuerzas conservadoras en una dimensión. En esta etapa se introducen ciertos conceptos auxiliares en mecánica como el trabajo y el poder. Luego mostramos que la mecánica newtoniana y cuántica son consistentes entre sí en el ámbito en el que se superponen, es decir, en el límite de la óptica geométrica de la mecánica cuántica. Por simplicidad, esta relación se desarrolla primero en una dimensión en el límite no relativista. Las dimensiones superiores requieren la introducción de derivadas parciales, y el caso relativista se considerará posteriormente.
Principios Fundamentales de la Dinámica
En términos generales, ha habido tres épocas de física, caracterizadas por tres respuestas diferentes a la pregunta de qué hace que las cosas salgan.
Dinámica Pre-Newtoniana
Aristóteles expuso una visión de la dinámica que concuerda estrechamente con nuestra experiencia cotidiana del mundo. Los objetos sólo se mueven cuando se ejerce una fuerza sobre ellos. Tan pronto como la fuerza desaparece, el objeto deja de moverse. El acto de empujar una caja por el piso ilustra este principio: ¡la caja ciertamente no se mueve por sí sola!
Dinámica newtoniana
En contraste con el comportamiento terrenal, los movimientos de los objetos celestes parecen sin esfuerzo. No hay fuerzas obvias que actúen para mantener los planetas en movimiento alrededor del sol. De hecho, parece que los objetos celestes simplemente se desplazan a velocidad constante a menos que algo actúe sobre ellos. La visión newtoniana de la dinámica —los objetos cambian su velocidad y no su posición cuando se ejerce una fuerza sobre ellos— se expresa en la segunda ley de Newton:
\[F = ma (Newton ’s second law ), \label{8.1}\]
donde\(F\) esta la fuerza ejercida sobre un cuerpo,\(m \) es su masa, y\(a\) es su aceleracion. La primera ley de Newton, que establece que un objeto permanece en reposo o en movimiento uniforme a menos que una fuerza actúe sobre él, es en realidad un caso especial de la segunda ley de Newton que se aplica cuando\(F\) = 0.
No es de extrañar que los primeros éxitos de la mecánica newtoniana estuvieran en el reino celeste, es decir, en las predicciones de órbitas planetarias. Se necesitó el genio de Newton para darse cuenta de que los mismos principios que guiaban a los planetas también se aplicaban al reino terrenal también. Desde el punto de vista newtoniano, la tendencia de los objetos a detenerse cuando dejamos de presionarlos es simplemente una consecuencia de las fuerzas de fricción que se oponen al movimiento. La fricción, que es tan importante en la tierra, es insignificante para los movimientos planetarios, razón por la cual la dinámica newtoniana es más obviamente válida para los cuerpos celestes.
Nótese que el principio de relatividad está estrechamente relacionado con la física newtoniana y es incompatible con los puntos de vista prenewtonianos. Después de todo, dos marcos de referencia que se mueven uno respecto al otro no pueden ser equivalentes en la vista prenewtoniana, porque los objetos sin nada empujándolos solo pueden llegar a descansar en uno de los dos marcos de referencia. La segunda ley de Newton obedece al principio de relatividad porque la aceleración de un objeto es la misma cuando se ve desde dos marcos de referencia diferentes que se mueven a una velocidad constante entre sí.
La relatividad de Einstein a menudo se ve como un repudio de Newton, pero esto está lejos de la verdad: la física newtoniana hace posible la teoría de la relatividad a través de su invención del principio de la relatividad. En comparación con las diferencias entre la dinámica prenewtoniana y la newtoniana, los cambios necesarios para pasar de la física newtoniana a la einsteiniana constituyen pequeños retoques.
Dinámica cuántica
En la mecánica cuántica, las partículas están representadas por ondas de materia, con el cuadrado absoluto del desplazamiento de onda produciendo la probabilidad de encontrar la partícula. El comportamiento de las partículas se deriva así de la reflexión, refracción, difracción e interferencia de las ondas asociadas. La conexión con la dinámica newtoniana proviene de trazar las trayectorias de los paquetes de ondas de materia. Los cambios en la velocidad y dirección de movimiento de estos paquetes corresponden a las aceleraciones de la mecánica clásica. Cuando las longitudes de onda son pequeñas en comparación con la escala de longitud natural del problema en cuestión, los paquetes de onda pueden hacerse pequeños, identificando así la posición de la partícula asociada, sin generar una incertidumbre excesiva en el momento de la partícula. Este es el límite de óptica geométrica de la mecánica cuántica.
Energía Potencial
Ahora abordamos la mecánica newtoniana en el caso donde la fuerza sobre una partícula es conservadora. Una fuerza conservadora es aquella que puede derivarse de una llamada energía potencial\(U\). Suponemos que la energía potencial de la partícula depende únicamente de su posición. La fuerza se obtiene de la energía potencial por la ecuación
\[F = - dU-. dx \label{8.2}\]
Usando esta ecuación escribimos la segunda ley de Newton como
\[ dU - ---= ma. dx \label{8.3} \]
Luego notamos que la aceleración puede escribirse en términos de la\(x \) derivada a lo largo de la trayectoria de la partícula de\(v\) 2\(∕\) 2:
\[ 2 a = dv-= dv-dx- = dv-v = 1-dv-. dt dx dt dx 2 dx \label{8.4} \]
El último paso en la derivación anterior se puede verificar aplicando la regla del producto:\(dv\) 2\(∕dt \) =\(d\) (\(vv\))\(∕dt \) =\(v\) (\(dv∕dt\)) + (\(dv∕dt\))\(v \) = 2\(v\) (\(dv∕dt\)). Al juntar las ecuaciones (8.3) y (8.4), encontramos que\(d\) (\(mv\)2\(∕\) 2 +\(U\))\(∕dt \) = 0, lo que implica que\(mv\) 2\(∕\) 2 +\(U \) es constante. Llamamos a esta constante la energía total\(E \) y a la cantidad\(K \) =\(mv\) 2\(∕\) 2 la energía cinética. Tenemos así el principio de conservación de energía para las fuerzas conservadoras:
\[E = K + U = constant. \label{8.5}\]
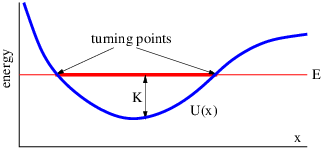
Recordemos que en mecánica cuántica el momento está relacionado con la velocidad del grupo\(u\) g por
\[Π = mug (momentum ) \label{8.6}\]
en el caso no relativista. Equiparar la velocidad del grupo\(v \) y eliminarla en la energía cinética da como resultado una expresión alternativa para esta cantidad:
\[ 2 K ≡ 1mu2g = -Π-- (kinetic energy). 2 2m \label{8.7} \]
Dado que la energía total\(E \) es constante o conservada, los incrementos en la energía potencial coinciden con disminuciones en la energía cinética y viceversa, como se ilustra en la figura 8.1. En la mecánica clásica la energía cinética no puede ser negativa, ya que es producto de la mitad de la masa y del cuadrado de la velocidad, ambas positivas. Así, una partícula con energía total\(E \) y energía potencial\(U \) está prohibida para incursionar en regiones en las que la energía cinética\(K \) =\(E \) -\(U \) es menor que cero.
Los puntos en los que la energía cinética es cero se denominan puntos de inflexión. Esto se debe a que una partícula disminuye en velocidad a medida que se acerca a un punto de inflexión, se detiene ahí por un instante e invierte la dirección. Tenga en cuenta también que una partícula con una energía total dada siempre tiene la misma velocidad en algún momento\(x \) independientemente de si se acerca a este punto desde la izquierda o la derecha:
\[ 1∕2 speed = |ug| = | ± [2(E - U)∕m ] |. \label{8.8}\]
La gravedad como fuerza conservadora
Un ejemplo de fuerza conservadora es la gravedad. Un objeto de masa\(m \) cerca de la superficie de la tierra tiene la energía potencial gravitacional
\[U = mgz (gravity near earth’s surface) \label{8.9}\]
donde\(z \) está la altura del objeto por encima de algún punto de referencia como la superficie terrestre y\(g \) = 9\(.\) 8 m s - 2 es el valor local del campo gravitacional cerca de la superficie. Observe que la energía potencial gravitacional aumenta hacia arriba. La velocidad del objeto en este caso es |\(u\) g | = [2 (\(E \)-\(mgz\))\(∕m\)] 1 2. Si se sabe que |\(u\) g | es igual al valor constante\(u\) 0 a la elevación\(z \) = 0, entonces las ecuaciones (8.8) y (8.9) nos dicen que\(u\) 0 = (2\(E∕m\)) 1 2 y |\(u\) g | = (\(u\)0 2 - 2\(gz\)) 1 2.
Hay ciertos tipos de preguntas que la conservación de energía no puede responder directamente. Por ejemplo, si un objeto es liberado en elevación\(h \) con velocidad cero a\(t \) = 0, ¿en qué momento alcanzará\(z \) = 0 bajo la influencia de la gravedad? En tales casos suele ser más fácil regresar a la segunda ley de Newton. Dado que la fuerza sobre el objeto es\(F \)\(dU∕dz \) = - = -\(mg \) en este caso, encontramos que la aceleración es\(a \) =\(F∕m \) = -\(mg∕m \) = -\(g\). Sin embargo,\(a \)\(du∕dt \) = =\(d\) 2\(z∕dt\) 2, entonces
\[u = - gt + C1 z = - gt2∕2 + C1t + C2 (constant gravity), \label{8.10}\]
donde\(C\) 1 y\(C\) 2 son constantes a determinar por las condiciones iniciales. Estos resultados se pueden verificar diferenciando para ver si se recupera la aceleración original. Desde\(u \) = 0 y\(z \) =\(h \) at\(t \) = 0, tenemos\(C\) 1 = 0 y\(C\) 2 =\(h\). Con estos resultados es fácil demostrar que el objeto alcanza\(z \) = 0 cuando\(t \) = (2\(h∕g\)) 1 2.
Poder
Cuando se ejerce una fuerza sobre un objeto, la energía se transfiere al objeto. La cantidad de energía transferida se llama el trabajo realizado sobre el objeto. Sin embargo, la energía solo se transfiere si el objeto se mueve. El trabajo\(W \) realizado es
\[W = F Δx \label{8.11}\]
donde la distancia movida por el objeto es Δ\(x \) y la fuerza ejercida sobre él es\(F\). Observe que el trabajo puede ser positivo o negativo. El trabajo es positivo si el objeto sobre el que se actúa se mueve en la misma dirección que la fuerza, ocurriendo un trabajo negativo si el objeto se mueve opuesto a la fuerza.
La ecuación (8.11) asume que la fuerza permanece constante sobre el desplazamiento completo Δ\(x\). Si no lo es, entonces es necesario dividir el desplazamiento en una serie de desplazamientos menores, sobre cada uno de los cuales se puede suponer que la fuerza es constante. El trabajo total es entonces la suma de las obras asociadas a cada pequeño desplazamiento.
Si más de una fuerza actúa sobre un objeto, las obras debido a las diferentes fuerzas cada una suman o restan energía, dependiendo de si son positivas o negativas. El trabajo total es la suma de estas obras individuales.
Hay dos casos especiales en los que el trabajo realizado sobre un objeto se relaciona con otras cantidades. Si\(F \) es la fuerza total que actúa sobre el objeto, entonces\(W \) =\(F\) Δ\(x \) =\(ma\) Δ\(x \) por la segunda ley de Newton. Sin embargo,\(a \) =\(dv∕dt \) donde\(v \) está la velocidad del objeto, y Δ\(x \) = (Δ Δ\(t\))\(x∕\) Δ\(t \) ≈ Δ\(t\), donde\(v\) Δ\(t \) es el tiempo requerido por el objeto para moverse a través de la distancia Δ\(x\). La aproximación se vuelve exacta cuando Δ\(x \) y Δ\(t \) se vuelven muy pequeñas. Poner todo esto en conjunto da como resultado
\[ dv d ( mv2 ) Wtotal = m ---vΔt = -- ----- Δt = ΔK (total work ), dt dt 2 \label{8.12} \]
donde\(K \) está la energía cinética del objeto. Así, cuando\(F \) es la única fuerza,\(W \) =\(W\) total es el trabajo total sobre el objeto, y esto equivale al cambio en la energía cinética del objeto. Esto se llama teorema trabajo-energía, y demuestra que el trabajo realmente es una transferencia de energía a un objeto.
El otro caso especial ocurre cuando la fuerza es conservadora, pero no es necesariamente la fuerza total que actúa sobre el objeto. En este caso
\[Wcons = - dU-Δx = - ΔU (conservative force), dx \label{8.13}\]
donde Δ\(U \) es el cambio en la energía potencial del objeto asociado a la fuerza de interés.
La potencia asociada a una fuerza es simplemente la cantidad de trabajo realizada por la fuerza dividida por el intervalo de tiempo Δ\(t \) sobre el cual se realiza. Por lo tanto, es la energía por unidad de tiempo transferida al objeto por la fuerza de interés. De la ecuación 8.11} vemos que el poder es
\[ FΔx P = -----= Fv (power ), Δt \label{8.14} \]
donde\(v \) es la velocidad a la que se mueve el objeto. El poder total es sólo la suma de los poderes asociados a cada fuerza. Es igual a la tasa de tiempo de cambio de la energía cinética del objeto:
\[Ptotal = Wtotal= dK-- (total power ). Δt dt \label{8.15}\]
Mecánica y Óptica Geométrica
Louis de Broglie 1 hizo una analogía entre las ondas de materia y las ondas de luz, señalando que los paquetes de ondas de luz cambian su velocidad como resultado de variaciones espaciales en el índice de refracción del medio en el que viajan. Este comportamiento se produce debido a que la relación de dispersión para la luz que viaja a través de un medio con índice de refracción\(n \) es\(ω \) =\(kc∕n\), de manera que la velocidad del grupo,\(u\) g =\(dω∕dk \) =\(c∕n\). Así, cuando\(n \) aumenta,\(u\) g disminuye, y viceversa. 2
En esta sección perseguimos la analogía de Broglie para ver si podemos llegar a una teoría de las ondas de la materia que dé los mismos resultados que la mecánica clásica en el límite de óptica geométrica de estas ondas. La relación de dispersión para las ondas de materia libre es\(ω \) = (\(k\)\(c\)2\(μ\) 2 + 2) 1 2. En el límite no relativista\(k\) \(c\)2 2\(μ\) 2. Como se hizo anteriormente, utilizamos (1 +\(ϵ\)) n ≈ 1 +\(nϵ \) para pequeños\(ϵ\). En el límite no relativista, la relación de dispersión para las ondas libres se convierte así
\[ω = μ (1 + k2c2∕μ2 )1∕2 ≈ μ + k2c2∕(2μ ). \label{8.16}\]
La ecuación anterior se puede transformar en la ecuación de energía total para una partícula libre, no relativista,\(E \) =\(mc\) 2 +\(K\), donde\(mc\) 2 es la energía de reposo y\(K \) es la energía cinética, multiplicando por \(ℏ\). Convertimos la ecuación de energía de partícula libre en la ecuación para una partícula sujeta a una fuerza conservadora agregando la energía potencial en\(U \) el lado derecho. El cambio análogo a la ecuación (8.16) es sumar\(S \) =\(U∕\)\(ℏ\) al lado derecho, dando como resultado una relación de dispersión modificada:
\[ω = S(x) + k2c2∕(2μ). \label{8.17}\]
(Dado que la energía de descanso es solo una constante, la hemos absorbido en\(S\).) Esto nos da la relación de dispersión para ondas de materia unidimensionales sujetas a una energía potencial espacialmente variable. La cantidad\(S\), que vemos es solo una energía potencial escalada, juega un papel para las ondas de materia que es análogo al papel desempeñado por un índice de refracción espacialmente variable para las ondas de luz.
Imaginemos ahora que todas las partes de la onda gobernadas por esta relación de dispersión oscilan en fase. La única forma en que esto puede suceder\(ω \) es si es constante, es decir, adquiere el mismo valor en todas las partes de la ola.
Si\(ω \) es constante, la única manera que\(S \) puede variar con\(x \) en la ecuación 8.17} es si el número de onda varía de manera compensatoria. Así, la frecuencia constante y la variación espacial\(S \) juntas implican que\(k \) =\(k\) (\(x\)). Resolviendo la ecuación (8.17) para\(k\) rendimientos
\[ [ ]1∕2 k(x) = ± 2μ[ω---S-(x-)] . c2 \label{8.18} \]
Dado que\(ω \) es constante, el número de onda se vuelve más pequeño y la longitud de onda más grande a medida que la onda se mueve hacia una región de aumento\(S\).
En el límite de la óptica geométrica, asumimos que eso\(S \) no cambia mucho sobre una longitud de onda de manera que la onda permanece razonablemente sinusoidal en forma con un número de onda aproximadamente constante en unas pocas longitudes de onda. Sin embargo, en distancias de muchas longitudes de onda se permite que el número de onda y la amplitud de la onda varíen considerablemente.
La velocidad de grupo calculada a partir de la relación de dispersión dada por la ecuación 8.17} es
\[ 2 ( 2 )1∕2 ug = dω-= kc--= ± 2c-(ω---S-) dk μ μ \label{8.19} \]
donde\(k \) se elimina en el último paso con ayuda de la ecuación 8.18}. La ecuación resultante nos dice cómo varía la velocidad del grupo a medida que una onda de materia atraviesa una región de variación lenta\(S\). Así, a\(S \) medida que aumenta,\(u\) g disminuye y viceversa.
Ahora podemos calcular la aceleración de un paquete de ondas resultante de la variación espacial en\(S\). Suponemos que\(x\) (\(t\)) representa la posición del paquete de ondas, de manera que\(u\) g =\(dx∕dt\). Usando la regla de la cadena\(du\) \(du\)g\(∕dt \) = (g\(∕dx\)\(dx∕dt\)) () = (\(du\)\(u\)g\(∕dx\) ) g, encontramos
\[ 2 2 a = dug-= dugu = dug∕2-= - c- dS-= - ¯h-dS-. dt dx g dx μ dx m dx \label{8.20} \]
La velocidad del grupo se elimina a favor de\(S \) al cuadrar la ecuación 8.19} y sustituyendo el resultado por la ecuación (8.20).
Recordando que\(U \) =\(ℏ\)\(S\), la ecuación 8.20} se convierte
\[ -1 dU- F- a = - m dx = m , \label{8.21}\]
¡que es solo la segunda ley de Newton! Así, el enfoque de óptica geométrica para el movimiento de partículas es completamente equivalente a la mecánica clásica de una partícula que se mueve bajo la influencia de una fuerza conservadora, al menos en una dimensión. Por lo tanto, tenemos dos formas de resolver para el movimiento de una partícula sujeta a una energía potencial\(U\) (\(x\)). Podemos aplicar los principios de la mecánica clásica para obtener la fuerza y la aceleración de la partícula, de la cual podemos derivar el movimiento. Alternativamente, podemos aplicar los principios de la óptica geométrica para calcular la velocidad espacialmente variable del paquete de ondas usando la ecuación 8.19}. Los resultados son completamente equivalentes, aunque los métodos son conceptualmente muy diferentes.
Tutorial — Derivadas parciales
Para entender la generalización de la mecánica newtoniana a dos y tres dimensiones, primero necesitamos entender un nuevo tipo de derivado llamado derivado parcial. La derivada parcial se utiliza en funciones de más de una variable. Es igual que una derivada ordinaria, excepto que al tomar la derivada de la función con respecto a una de las variables, las otras variables se mantienen constantes. Como ejemplo, consideremos la función
\[ 4 2 2 4 f(x,y) = Ax + Bx y + Cy \label{8.22}\]
donde\(A\),\(B\), y\(C \) son constantes. La derivada parcial de\(f \) con respecto a\(x\) es
\[∂f --- = 4Ax3 + 2Bxy2 ∂x \label{8.23} \]
y la derivada parcial con respecto a\(y \) es
\[∂f 2 3 ---= 2Bx y + 4Cy . ∂y \label{8.24} \]
¡Eso es! Tenga en cuenta que se usa un símbolo especial “\(∂\)” en lugar del “\(d\)” normal para la derivada parcial. Esto a veces se llama una “d rizada”.
Movimiento en Dos y Tres Dimensiones
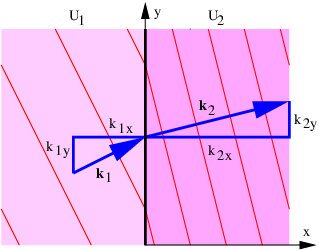
Cuando una onda de materia se mueve a través de una región de energía potencial variable en una dimensión, solo cambia el número de onda. En dos o tres dimensiones, el vector de onda puede cambiar tanto en dirección como en magnitud. Esto complica el cálculo del movimiento de las partículas. No obstante, ya tenemos un ejemplo de cómo manejar esta situación, es decir, la refracción de la luz. En ese caso la ley de Snell nos dice cómo cambia la dirección del vector de onda, mientras que la relación de dispersión combinada con la constancia de la frecuencia nos da información sobre el cambio en la magnitud del vector de onda. Para las ondas de materia funciona un procedimiento similar, aunque los detalles son diferentes, porque buscamos las consecuencias de un cambio en la energía potencial más que un cambio en el índice de refracción.
La Figura 8.2 ilustra la refracción de las ondas de materia a una discontinuidad en la energía potencial. Supongamos que la discontinuidad ocurre en\(x \) = 0. Si la onda de materia a la izquierda de la discontinuidad es\(ψ\) 1 = sin (\(k\)1 x\(x \) +\(k\) 1 y\(y \) -\(ω\) 1 \(t\)) y a la derecha es\(ψ\) 2 = sin (\(k\)2 x\(x \) +\(k\) 2 y\(y \) -\(ω\) 2\(t\)), entonces los frentes de onda de las ondas coincidirán a través de la discontinuidad para todos los tiempos solo si\(ω\) 1 =\(ω\) 2 ≡\(ω \) y\(k\) 1 y =\(k\) 2 y ≡\(k\) y. Ya estamos familiarizados con la primera condición del problema unidimensional, por lo que el único ingrediente nuevo es la constancia del\(y\) componente del vector de onda.
En dos dimensiones el momento es un vector:\(Π\) =\(m\)\(u\) cuando |\(u\)\(c\) |, donde\(u\) está la velocidad de la partícula. Además, la energía cinética es\(K \) =\(m\) \(u\)| |\(∕\) 2 2 = |\(Π\) | 2\(∕\) (2\(m\)) = (π x 2 + Π y 2)\(∕\) (2\(m\)). La relación entre la energía cinética, potencial y total no ha cambiado desde el caso unidimensional, por lo que tenemos
\[ 2 2 E = U + (Πx + Π y)∕(2m ) = constant. \label{8.25}\]
La relación de Broglie nos dice que\(Π\) =\(ℏ\)\(k\), así la constancia de\(k\) y a través de la discontinuidad en nos\(U \) dice que
\[Πy = constant \label{8.26}\]
ahí.
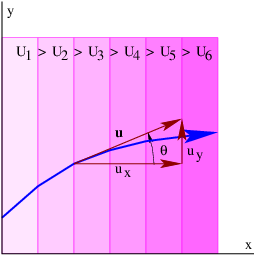
Ahora aproximemos una variable continua\(U\) (\(x\)) por una serie de pasos de constante\(U \) orientada normal al\(x \) eje. El análisis anterior se puede aplicar en los saltos o discontinuidades\(U \) entre pasos, como se ilustra en la figura 8.3, con el resultado de que las ecuaciones (8.25) y (8.26) son válidas en todas las discontinuidades. Si ahora dejamos que el ancho del paso vaya a cero, estas ecuaciones entonces se vuelven válidas para\(U \) continuamente variable in\(x\).
Un ejemplo de la mecánica clásica de un problema de este tipo es una bola rodando por una rampa inclinada con un componente de velocidad inicial a través de la rampa, como se ilustra en la figura 8.4. La energía potencial disminuye en la dirección de la rampa descendente, lo que resulta en una fuerza hacia abajo de la rampa. Esto acelera la pelota en esa dirección, pero deja sin cambios el componente de impulso a través de la rampa.
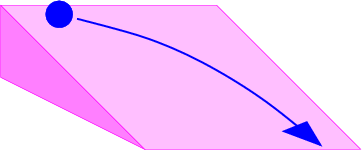
Usando el procedimiento que invocamos antes, encontramos que los componentes de fuerza asociados con\(U\) (\(x\)) en las\(y \) direcciones\(x \) y son\(F\) x = -\(dU∕dx \) e\(F\) y = 0. Esto generaliza a
\[ ( ) ∂U-- ∂U--∂U-- F = - ∂x ,∂y , ∂z (3-D conservative force) \label{8.27} \]
en el caso tridimensional donde la orientación de\(U \) las superficies constantes es arbitraria. También es válido cuando\(U\) (\(x,y,z\)) no se limita a una simple forma de rampa, sino que adquiere una estructura completamente arbitraria.
Las definiciones de trabajo y poder son ligeramente diferentes en dos y tres dimensiones. En particular, el trabajo se define como
\[W = F ⋅ Δx \label{8.28}\]
donde Δ\(x\) es ahora un desplazamiento vectorial. El carácter vectorial de esta expresión produce una posibilidad adicional sobre el caso unidimensional, donde el trabajo es positivo o negativo dependiendo de la dirección de Δ\(x\) relativo a\(F\). Si la fuerza y el desplazamiento del objeto sobre el que actúa la fuerza son perpendiculares entre sí, el trabajo realizado por la fuerza es en realidad cero, aunque tanto la fuerza como el desplazamiento tengan magnitudes distintas de cero. El poder exhibe un cambio similar:
\[P = F ⋅ u. \label{8.29}\]
Así, la potencia es cero si la velocidad de un objeto es normal a la fuerza que se ejerce sobre él.
Como en el caso unidimensional, el trabajo total realizado sobre una partícula equivale al cambio en la energía cinética de la partícula. Además, el trabajo realizado por una fuerza conservadora equivale a menos el cambio en la energía potencial asociada.
La conservación de energía por sí misma es algo menos útil para resolver problemas en dos y tres dimensiones que en una dimensión. Esto se debe a que conocer la energía cinética en algún momento nos dice solo la magnitud de la velocidad, no su dirección. Si la conservación de la energía no nos da la información que necesitamos, entonces debemos volver a la segunda ley de Newton, como hicimos en el caso unidimensional. Por ejemplo, si un objeto de masa\(m\) tiene una velocidad inicial\(u\) 0 = (\(u\)0\(, \) 0) en la ubicación (\(x,z\)) = (0\(,h\)) y tiene la energía potencial gravitacional\(U \) =\(mgz\), entonces la fuerza sobre el objeto es\(F\) = (0\(,\) -\(mg\)). Por lo tanto, la aceleración es\(a\)\(F\)\(∕m \) = = (0\(,\) -\(g\)). Dado que\(a\)\(d\)\(u\)\(∕dt \) = =\(d\) \(x\)\(∕dt\)2 2 donde\(x\) = (\(x,z\)) es la posición del objeto, encontramos que
\[ 2 u = (C1,- gt + C2) x = (C1t + C3, - gt∕2 + C2t + C4 ), \label{8.30}\]
donde\(C\) 1,\(C\) 2,\(C\) 3 y\(C\) 4 son constantes a evaluar para que la solución se reduzca a las condiciones iniciales a\(t \) = 0. Las condiciones iniciales especificadas nos dicen que\(C\) 1 =\(u\) 0,\(C\) 2 = 0,\(C\) 3 = 0 y\(C\) 4 =\(h \) en este caso. A partir de estos resultados podemos inferir la posición y velocidad del objeto en cualquier momento.
Momentum cinético y total
Si previamente has tomado un curso de física entonces probablemente hayas notado que se usa un símbolo bastante extraño para el impulso, es decir\(Π\), en lugar del empleado más comúnmente\(p\). La razón de este uso peculiar es que en realidad hay dos tipos de impulso, impulso cinético y impulso total, así como hay dos tipos de energía, cinética y total. 3 El símbolo\(Π\) representa el impulso total mientras que\(p\) representa el impulso cinético. Normalmente no necesitamos distinguir entre las dos cantidades, ya que generalmente son iguales entre sí. No obstante, más adelante en el curso encontraremos que es crucial hacer esta distinción en el caso de partículas cargadas en un campo magnético. Como regla general, el impulso total se relaciona con el vector de onda de una partícula a través de la relación de Broglie,\(Π\) =\(ℏ\)\(k\), mientras que el impulso cinético está relacionado con la velocidad de una partícula,\(p\) =\(m\)\(u\)\(∕\) (1 -\(u\) 2\(∕c\) 2) 1 2.
Problemas
- Supongamos que la relación de dispersión para una onda de materia bajo ciertas condiciones es\(ω \) =\(μ \) + (\(k \)-\(a\)) \(c\)2 2\(∕\) (2\(μ\)) donde\(k \) está el número de onda de la onda,\(μ \) = \(mc\)2\(∕\)\(ℏ\),\(m \) es la masa de la partícula asociada,\(a \) es una constante,\(c \) es la velocidad de la luz, y\(ℏ\) es la constante de Planck dividida por 2\(π\).
- Utilice esta relación de dispersona y las relaciones Planck y de Broglie para determinar la relación entre energía\(E\), impulso π y masa\(m\).
- Calcule la velocidad de grupo de la onda y utilícela para determinar cómo la velocidad del grupo depende de la masa y el momento en este caso.
- Una función de onda de materia asociada a una partícula de energía total definida (constante)\(E \) toma la forma mostrada en la figura 8.5. Haga un boceto que muestre cómo varían las energías cinéticas, potenciales y totales de la partícula\(x\).
Figura 8.5: Una función de onda en la que la longitud de onda varía con la posición.
_____________________________________
- Computación\(∂∕∂x \) y\(∂∕∂y \) de las siguientes funciones. Otros símbolos son constantes.
- \(f\)(\(x,y\)) =\(ax\) 2 +\(by\) 3
- \(f\)(\(x,y\)) =\(ax\) 2\(y\) 2
- \(f\)(\(x,y\)) = (\(x \)+\(a\))\(∕\) (\(y \)+\(b\))
- Dada una energía potencial para una partícula de masa\(M \) de la forma\(U\) (\(x\)) =\(Ax\) 3 -\(Bx\) donde\(A \) y\(B \) son constantes positivas:
- Encuentra la fuerza sobre la partícula.
- Encuentra los valores de\(x \) donde la fuerza es cero.
- Sketch\(U\) (\(x\)) versus\(x \) y compara gráficamente la pendiente de\(U\) (\(x\)) con la fuerza calculada anteriormente. ¿Los dos coinciden cualitativamente?
- Si la energía total de la partícula es cero, ¿dónde están sus puntos de inflexión?
- ¿Cuál es la velocidad de la partícula en función de la posición asumiendo que\(E \) se conoce la energía total?
- Dada una función de energía potencial\(U\) (\(x,y\)) =\(A\) (\(x\)2 +\(y\) 2) donde\(A \) es una constante positiva:
- Esboce líneas de constante\(U \) en el\(y \) plano\(x\) -.
- Calcular los componentes de la fuerza en función de\(x \)\(y \) y dibujar vectores de fuerza de muestra en el\(y \) plano\(x\) - en la misma parcela utilizada anteriormente. ¿Los vectores de fuerza apuntan “cuesta arriba” o “cuesta abajo”?
- Haga lo mismo que en la pregunta anterior para la función de energía potencial\(U\) (\(x,y\)) =\(Axy\).
- Supongamos que los componentes del vector de fuerza en el\(y \) plano\(x\) - son\(F\) = (2\(Axy\) \(, \)3 3\(Ax\) 2\(y\) 2) donde\(A \) es una constante. A ver si se puede encontrar una función energética potencial\(U\) (\(x,y\)) que da lugar a esta fuerza.
- Estás parado en lo alto de un acantilado de altura\(H \) con una roca de masa\(M\).
- Si lanzas la roca horizontalmente hacia afuera a la velocidad\(u\) 0, ¿cuál será su velocidad cuando golpee el suelo de abajo?
- Si lanzas la roca hacia arriba a 45° a la horizontal a velocidad\(u\) 0, ¿cuál será su velocidad cuando golpee el suelo?
Pista: ¿Se puede utilizar la conservación de energía para resolver este problema? Ignorar la fricción del aire
- Un carro de masa 1200 kg inicialmente moviéndose 30 m s - 1 frena a una parada.
- ¿Cuál es el trabajo neto realizado en el automóvil debido a todas las fuerzas que actuaron sobre él durante el periodo indicado?
- Describir el movimiento del automóvil en relación con un marco de referencia inercial que inicialmente se mueve con el automóvil.
- En el marco de referencia anterior, ¿cuál es el trabajo neto realizado en el automóvil durante el periodo indicado?
¿Es el trabajo una cantidad relativisticamente invariante?
Figura 8.6: La trayectoria de un balón de fútbol.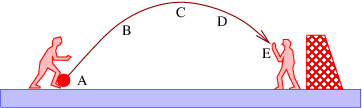
_____________________________________
- Un futbolista patea una pelota de fútbol, la cual es atrapada por el portero como se muestra en la figura 8.6. En diversos puntos las fuerzas ejercidas por la gravedad, la fricción aérea, el pie del jugador ofensivo, y las manos del portero actúan sobre el balón.
- Enumere las fuerzas que actúan sobre el balón de fútbol en cada uno de los puntos A, B, C, D y E.
- Indique si la potencia instantánea que se aplica al balón de fútbol debido a cada una de las fuerzas enumeradas anteriormente es positiva, negativa o cero en cada uno de los puntos etiquetados.
- Un cañón ubicado en (\(x,z\)) = (0\(, \) 0) dispara una bala de cañón hacia arriba en un ángulo de\(θ \) desde la horizontal a la velocidad inicial\(u\) 0. Pista: Para resolver este problema primero debes obtener los\(z \) componentes\(x \) y de la aceleración de la segunda ley de Newton. Segundo, debes encontrar los componentes de velocidad en función del tiempo a partir de los componentes de aceleración. Tercero, hay que encontrar\(x \) y\(z \) en función del tiempo a partir de los componentes de la velocidad. Solo entonces debes intentar responder a las preguntas a continuación.
- ¿Cuánto tiempo tarda la bola de cañón en alcanzar su máxima altitud?
- ¿Qué tan alto va la bola de cañón?
- ¿A qué valor de\(x \) la bala de cañón golpea el suelo (\(z \)= 0)?
- Determinar qué valor de\(θ \) rinde el rango máximo.
Capítulo 9 Simetría y Estados Encuadernados
Cuando se inventó la mecánica cuántica por primera vez, los principios dinámicos utilizados fueron los mismos que los subyacentes a la mecánica clásica. El desarrollo inicial del campo procedió en gran medida imponiendo leyes cuánticas sobre variables clásicas como la posición, el impulso y la energía. Sin embargo, a medida que avanzaba la mecánica cuántica, quedó claro que había muchas situaciones en las que no existían análogos clásicos para nuevos tipos de sistemas mecánicos cuánticos, especialmente aquellos que surgieron en el estudio de partículas elementales. Para entender estos sistemas fue necesario buscar orientación de fuentes novedosas. Una de las fuentes más importantes fue la idea de simetría, y en particular la relación entre simetría y variables conservadas. Este tipo de relación fue desarrollada por primera vez a principios del siglo XX por el matemático alemán Emmy Nöther en el contexto de la mecánica clásica. Sin embargo, su idea es más fácil de expresar y usar en la mecánica cuántica que en la mecánica clásica. Emmy Nöther demostró que existe una relación entre las simetrías de un sistema y las variables dinámicas conservadas. Esta idea se llama naturalmente el teorema de N öther.
En la mecánica clásica una partícula está unida o confinada a una región en particular si su energía total excede la energía potencial solo en esta región. En la mecánica cuántica, las ondas de materia también pueden ser confinadas por la misma razón, aunque el confinamiento suele ser menos perfecto que en el caso clásico. En este capítulo examinamos las consecuencias del confinamiento de olas. Primero miramos la llamada “partícula en una caja” en una dimensión espacial. Encontramos que las partículas confinadas solo pueden tomar valores discretos de energía. Cuando el confinamiento no es perfecto, vemos cómo una partícula mecánica cuántica puede filtrarse a través de una barrera de energía potencial que es clásicamente impenetrable. El movimiento de una partícula sobre un anillo circular nos lleva a otra forma de confinamiento y a la introducción del momento angular. Esto nos lleva finalmente a una discusión sobre el momento intrínseco o angular de giro de las partículas elementales.
Tutorial — Ondas Complejas
Hasta ahora hemos representado ondas planas mecánicas cuánticas por funciones sinusoidales y coseno, al igual que con otros tipos de ondas. Sin embargo, las ondas de materia plana no pueden ser verdaderamente representadas por senos y cosenos. En cambio, necesitamos funciones matemáticas en las que el desplazamiento de las olas sea complejo y no real. Esto requiere la introducción de un poco de nuevas matemáticas, que abordamos primero. Usando nuestra nueva herramienta matemática, podemos explorar dos ideas de importancia crucial en la mecánica cuántica; (1) la relación entre la simetría y las leyes de conservación, y (2) la dinámica de las ondas espacialmente confinadas.
Un número complejo\(z \) es la suma de un número real y un número imaginario. Un número imaginario es solo un número real multiplicado por\(i \) ≡ (- 1) 1 2. Así, podemos escribir\(z \) =\(a \) +\(ib \) para cualquier complejo\(z\), donde\(a \) y\(b \) son reales. Las cantidades\(a\) y\(b \) son las partes reales e imaginarias de\(z\), a veces escritas Re (\(z\)) e Im (\(z\)).
La mecánica cuántica requiere que las funciones de onda sean complejas, es decir, poseer partes reales e imaginarias. Las ondas planas en la mecánica cuántica en realidad toman la forma\(ψ \) = exp [\(i\)(\(kx \)-\(ωt\))] en lugar de, digamos, cos (\(kx \)-\(ωt\)). La razón de esto es la necesidad de distinguir entre ondas con frecuencias positivas y negativas. Si reemplazamos\(k \) y\(ω \) con -\(k \) y -\(ω \) en forma coseno, obtenemos cos (-\(kx \) +\(ωt\)) = cos [- (\(kx \)-\(ωt\))] = cos (\(kx \)-\(ωt\)). En otras palabras, cambiar el signo de\(k \) y no da como\(ω \) resultado ningún cambio en una onda expresada como una función coseno. Los dos estados mecánicos cuánticos, uno con número de onda y frecuencia\(k \)\(ω \) y el otro con -\(k \) y -\(ω\), producen funciones de onda indistinguibles y por lo tanto representarían estados físicamente indistinguibles. Por lo tanto, la forma coseno es insuficientemente flexible para representar ondas mecánicas cuánticas. Por otro lado, si reemplazamos\(k \) y\(ω \) con sus negativos en la compleja forma exponencial de una onda plana obtenemos\(ψ \) = exp [-\(i\) (\(kx \)-\(ωt\))], que es diferente de exp [\(i\)(\(kx \)- \(ωt\))]. Estas dos funciones de onda son distinguibles y, por lo tanto, corresponden a distintos estados físicos.
No es inmediatamente obvio que una función exponencial compleja proporciona el comportamiento oscilatorio necesario para representar una onda plana. Sin embargo, el exponencial complejo se puede expresar en términos de senos y cosenos usando la ecuación de Euler:
\[exp(iϕ) = cos(ϕ) + isin(ϕ) (Euler’s equation). \label{9.1}\]
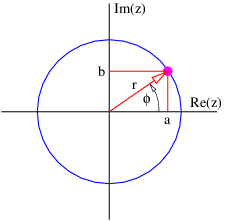
Si definimos\(r \) = (\(a\)2 +\(b\) 2) 1 2 y\(ϕ \) = tan - 1 (\(b∕a\)), entonces una forma alternativa de expresar un complejo número es\(z \) =\(r\) exp (\(iϕ\)), que por la ecuación de Euler es igual a\(r\) cos (\(ϕ\)) +\(ir\) sin (\(ϕ\)). La comparación muestra que\(a \) =\(r\) cos (\(ϕ\)) y\(b \) =\(r\) sin (\(ϕ\)). Así, un número complejo puede pensarse como un punto en el\(a\) -\(b \) plano con coordenadas cartesianas\(a \) y\(b \) y coordenadas polares\(r \) y\(ϕ\). El\(b \) plano\(a\) - se llama el plano complejo.
Ahora vemos cómo la función de onda compleja representa una oscilación. Si\(ψ \) = exp [\(i\)(\(kx\)-\(ωt\))], la función compleja\(ψ\) (\(x,t\)) se mueve alrededor y redondea el círculo unitario en el plano complejo como\(x \) y\(t \) cambia, como se ilustra en la figura 9.1. Esto contrasta con la oscilación de ida y vuelta a lo largo del eje horizontal del plano complejo representado por cos (\(kx \)-\(ωt\)).
No presentaremos una prueba formal de la ecuación de Euler —eventualmente la verás en tu curso de cálculo. Sin embargo, puede ser útil señalar que las\(ϕ \) derivadas de exp (\(iϕ\)) y cos (\(ϕ\)) +\(i\) sin (\(ϕ\)) tienen el mismo comportamiento:
\[ d ---exp(iϕ) = iexp (iϕ ); dϕ \label{9.2} \]
\[ d dϕ-[cos(ϕ ) + i sin(ϕ )] = - sin(ϕ ) + icos(ϕ ) = i[cos(ϕ) + isin (ϕ)]. \label{9.3} \]
(En la segunda de estas ecuaciones hemos reemplazado el signo menos frente a la función sinusoidal por\(i\) 2 y luego hemos extraído un factor común de\(i\).) La\(ϕ \) derivada de ambas funciones devuelve así la función de nuevo veces\(i\). Este es un fuerte indicio de que exp (\(iϕ\)) y cos (\(ϕ\)) +\(i\) sin (\(ϕ\)) son diferentes formas de representar la misma función.
Indicamos el conjugado complejo de un número complejo\(z \) mediante un asterisco superíndice, es decir,\(z\) *. Se obtiene sustituyendo\(i \) por -\(i\). Así, (\(a \)+\(ib\)) * =\(a\) -\(ib\). El cuadrado absoluto de un número complejo es el número multiplicado por su conjugado complejo:
\[|z|2 = |a + ib|2 ≡ (a + ib)(a - ib) = a2 + b2 = r2. \label{9.4}\]
Observe que el cuadrado absoluto de una función exponencial compleja es uno:
\[ 2 |exp(iϕ)| = exp (iϕ)exp (- iϕ) = exp (iϕ - iϕ) = exp (0) = 1. \label{9.5}\]
En mecánica cuántica el cuadrado absoluto de la función de onda en cualquier punto expresa la probabilidad relativa de encontrar la partícula asociada en ese punto. Así, la probabilidad de encontrar una partícula representada por una onda plana es uniforme en el espacio. Contraste esto con la probabilidad relativa asociada a una onda sinusoidal: | sin (\(kx \)-\(ωt\)) | 2 = sin 2 (\(kx \)-\(ωt\)). Esto varía de cero a uno, dependiendo de la fase de la onda. La “ondulación” en una onda plana exponencial compleja reside en la fase más que en la magnitud de la función de onda.
Se necesita una pieza más de matemáticas. El complejo conjugado de la ecuación de Euler es
\[exp(- iϕ) = cos(ϕ) - isin(ϕ). \label{9.6}\]
Tomando la suma y la diferencia de esto con la ecuación original de Euler da como resultado la expresión del seno y el coseno en términos de exponenciales complejos:
\[cos(ϕ ) = exp(iϕ) +-exp(--iϕ)- sin(ϕ) = exp-(iϕ)---exp-(--iϕ). 2 2i \label{9.7}\]
No estamos acostumbrados a que aparezcan números complejos en las teorías físicas y es difícil imaginar cómo mediríamos tal número. Sin embargo, todo lo observable proviene de tomar el cuadrado absoluto de una función de onda, por lo que tratamos solo con números reales en experimentos.
Simetría y Mecánica Cuántica
La idea de simetría juega un papel muy importante en la física. Ya hemos utilizado argumentos de simetría en la teoría de la relatividad —aplicar el principio de relatividad para obtener la relación de dispersión para las ondas relativistas de materia es precisamente un argumento así. En esta sección comenzamos a explorar cómo se puede utilizar la simetría para aumentar nuestra comprensión de la mecánica cuántica.
Partícula
Para nuestro primer ejemplo tomamos el caso de una partícula libre en mecánica cuántica, es decir, una partícula sujeta a ninguna fuerza. La función de onda para una partícula libre de impulso definido π y energía\(E\) viene dada por
\[ψ = exp [i(kx - ωt )] = exp [i(Πx - Et)∕¯h\label{free particle}\]. \ label {9.8}\]
Para esta función de onda |\(ψ\) | 2 = 1 en todas partes, por lo que la probabilidad de encontrar la partícula en cualquier lugar del espacio y el tiempo es uniforme. Esto contrasta con la distribución de probabilidad que surge si asumimos que una partícula libre tiene la función de onda\(ψ \) = cos [(π\(x \) -\(Et\))\(∕\)\(ℏ\)]. En este caso |\(ψ\) | 2 = cos 2 [(π\(x \) -\(Et\))\(∕\)\(ℏ\)], que varía con la posición y el tiempo, y es inconsistente con una distribución de probabilidad uniforme.
Simetría y definitividad
La mecánica cuántica es una teoría probabilística, en el sentido de que las predicciones que hace nos dicen, por ejemplo, la probabilidad de encontrar una partícula en algún lugar del espacio. Si no sabemos nada sobre la historia previa de una partícula, y si no hay restricciones físicas que hagan más probable que una partícula esté en un punto a lo largo del\(x \) eje que en cualquier otro, entonces la distribución de probabilidad debe ser\(P\) (\(x\)) =\(constant\).
Este es un ejemplo de un argumento de simetría. Expresado de manera más formal, establece que si se aplican las condiciones anteriores, entonces la distribución de probabilidad debería estar sujeta a la condición\(P\) (\(x \)+\(D\)) =\(P\) (\(x\)) para cualquier valor constante de\(D\). El único posible\(P\) (\(x\)) en este caso es\(P \) =\(constant\). En el lenguaje de la física, si no hay nada que le dé a la partícula una mayor probabilidad de estar en un punto más que en otro, entonces la probabilidad es independiente de la posición y el sistema es invariante bajo desplazamiento en la\(x\) dirección.
El argumento anterior no es suficiente para la mecánica cuántica, ya que como hemos aprendido, la cantidad fundamental que describe una partícula no es la distribución de probabilidad, sino la función de onda\(ψ\) (\(x\)). Así, la función de onda más que la distribución de probabilidad debería ser la cantidad que es invariante bajo desplazamiento, es decir,\(ψ\) (\(x \)+\(D\)) =\(ψ\) (\(x\)).
Esta condición resulta ser demasiado restrictiva, porque implica que\(ψ\) (\(x\)) =\(constant\), mientras que sabemos que una onda plana unidimensional, que describe una partícula con una probabilidad uniforme de ser encontrada en cualquier parte del\(x \) eje, tiene la forma\(ψ\) (\(x\)) = exp (\(ikx\)). (Por simplicidad ignoramos temporalmente la dependencia del tiempo). Si hacemos la sustitución\(x \) →\(x \) +\(D\) en una onda plana, obtenemos exp [\(ik\)(\(x \)+\(D\))] = exp (\(ikx\)) exp (\(ikD\)). Por lo tanto, la función de onda no es técnicamente invariante bajo desplazamiento, ya que la función de onda desplazada se multiplica por el factor exp (\(ikD\)). Sin embargo, la distribución de probabilidad de la función de onda desplazada sigue siendo igual a una en todas partes, por lo que no hay cambio en lo que observamos. Así, al determinar la invarianza bajo desplazamiento, se nos permite ignorar los cambios en la función de onda que consisten únicamente en multiplicarla por una constante compleja con un valor absoluto de uno. Tal constante multiplicativa se llama factor de fase.
Es fácil convencerse por ensayo y error o por medios más sofisticados de que la única forma de función de onda\(ψ\) (\(x\)) que satisface la condición\(ψ\) (\(x \)+\(D\)) =\(ψ\) (\(x\)) × (factor de fase) es\(ψ\) (\(x\)) = \(A\)exp (\(ikx\)) donde\(A \) es una constante (posiblemente compleja). Esto es solo en forma de una onda plana exponencial compleja con número de onda\(k\). Así, no sólo la función de onda exponencial compleja es invariante bajo desplazamientos de la manera definida anteriormente, sino que es la única función de onda que es invariante a los desplazamientos. Además, el factor de fase que aparece para un desplazamiento\(D \) de tal onda plana toma la forma exp (\(iC\)) = exp (\(ikD\)), donde\(k \) es el número de onda de la onda plana.
Como experimento, veamos si un paquete de ondas es invariante bajo desplazamiento. Definamos un paquete de ondas que consta de dos ondas planas:
\[ψ (x) = exp(ik1x) + exp(ik2x). \label{9.9}\]
Hacer la sustitución\(x \) →\(x \) +\(D \) en este caso da como resultado
\[ψ(x + D ) = exp [ik1(x + D )] + exp [ik2(x + D )] = exp (ik1x)exp (ik1D ) + exp(ik2x)exp (ik2D ) ⁄= [exp (ik1x) + exp (ik2x )] × (phase factor). \label{9.10} \]
La imposibilidad de escribir\(ψ\) (\(x \)+\(D\)) =\(ψ\) (\(x\)) × (factor de fase) da plausibilidad a la afirmación de que un único exponencial complejo es la única forma posible de la función de onda que es invariante bajo desplazamiento.
Observe que el paquete de ondas no tiene número de onda definido, y por lo tanto, impulso. En particular, el paquete de ondas es una suma de exponenciales complejos con números de onda\(k\) 1 y\(k\) 2, lo que significa que la partícula asociada puede tener un impulso π 1 =\(ℏ\)\(k\) 1 o Π 2 =\(ℏ\)\(k\) 2. Esto tiene sentido desde el punto de vista del principio de incertidumbre —para una sola onda plana la incertidumbre en la posición es completa y la incertidumbre en el impulso es cero. Para un paquete de onda se reduce la incertidumbre en la posición y la incertidumbre en el impulso es distinta de cero. Como hemos visto, esta idea se puede llevar más allá: Un valor definido de impulso debe asociarse con una distribución de probabilidad completamente indefinida en posición, es decir, con\(P \) =\(constant\). Esto corresponde a una función de onda que tiene la forma de una onda plana exponencial compleja. Sin embargo, dicha onda plana es invariante bajo desplazamiento\(D\), a excepción del factor de fase multiplicativo exp (\(ikD\)), el cual no tiene consecuencias físicas ya que desaparece cuando se obtiene la distribución de probabilidad. Así, vemos que la invarianza bajo desplazamiento de la función de onda y un valor definido del impulso están ligadas, en que cada una implica la otra:
\[invariance under displacement ⇐ ⇒ definite momentum \label{9.11}\]
La idea de energía potencial se introdujo en el capítulo anterior. En particular, encontramos que si la energía total es constante, entonces el impulso no puede ser constante en presencia de energía potencial espacialmente variable. Esto significa que el número de onda, y por lo tanto la longitud de onda de las oscilaciones en la función de onda también varían con la posición. La falta de homogeneidad espacial de la energía potencial da lugar a una inhomogeneidad espacial en la función de onda y, por lo tanto, a un impulso indefinido.
El argumento anterior se puede extender a otras variables además del momentum. En particular dado que la dependencia temporal de una onda plana exponencial compleja es exp (-\(iωt\)) = exp (-\(iEt∕\)\(ℏ\)), donde\(E \) está la energía total, tenemos por analogía con el argumento anterior que
\[invariance under time shift ⇐⇒ de finite energy. \label{9.12}\]
Así, la invarianza de la función de onda bajo un desplazamiento en el tiempo implica un valor definido de la energía de la partícula asociada.
En el capítulo anterior asumimos que la frecuencia (y por lo tanto la energía) era definida y constante para una partícula que pasaba por una región de energía potencial variable. Ahora vemos que esta suposición sólo se justifica si la energía potencial no cambia con el tiempo. Esto se debe a que una energía potencial variable en el tiempo elimina la posibilidad de invarianza bajo el cambio de tiempo.
Invarianza
Hemos visto algunos ejemplos de invarianza en la mecánica cuántica. Ahora es el momento de definir este concepto con mayor precisión. Se dice que una función de onda mecánica cuántica es invariante bajo alguna transformación si la función de onda transformada es observacionalmente indistinguible de la original.
En los ejemplos anteriores, la transformación se logra reemplazando\(x \) por\(x \) +\(D \) en el caso de desplazamiento en el espacio y de manera similar reemplazando\(t \) por\(t \) +\(T\) para desplazamiento en el tiempo. No obstante, la idea de una transformación es mucho más general; se discutirán otros ejemplos a medida que vayan surgiendo.
La idea de “observacionalmente indistinguible” puede ser complicada. Por ejemplo, si alguna transformación da como resultado una función de onda nueva que es la función de onda antigua multiplicada por un factor de fase constante, entonces la función de nueva onda es observacionalmente indistinguible de la anterior. Esto se debe a que las mediciones físicas capturan diferencias de fase entre diferentes partes de las funciones de onda (piense en cómo funcionan los interferómetros), pero no fases absolutas. El factor de fase constante desaparece en este cálculo de diferencia. Sin embargo, si el factor de fase multiplicativo creado por alguna transformación es una función de la posición, entonces la diferencia de fase entre diferentes partes de una función de onda cambia como resultado de la transformación. La función de onda no es invariante bajo esta transformación.
Variables compatibles
Ya sabemos que los valores definidos de ciertos pares de variables no se pueden obtener simultáneamente en la mecánica cuántica. Por ejemplo, la indefinición de la posición y el impulso están relacionados por el principio de incertidumbre —un valor definido de posición implica un valor indefinido del impulso y viceversa. Si se pueden obtener simultáneamente valores definidos de dos variables, entonces llamamos a estas variables compatibles. Si no, las variables son incompatibles.
Si la función de onda de una partícula es invariante bajo los desplazamientos asociados a ambas variables, entonces las variables son compatibles. Por ejemplo, la onda plana exponencial compleja asociada a una partícula libre es invariante bajo desplazamientos tanto en el espacio como en el tiempo. Dado que el impulso está asociado con los desplazamientos espaciales y la energía con los desplazamientos temporales, el impulso y la energía son variables compatibles para una partícula libre.
Compatibilidad y Conservación
Las variables compatibles con la energía tienen un estatus especial. La función de onda que corresponde a un valor definido de tal variable es invariante a los desplazamientos en el tiempo. En otras palabras, la función de onda no cambia bajo este desplazamiento excepto por un factor de fase trivial. Así, si la función de onda también es invariante a alguna otra transformación en un momento determinado, es invariante a esa transformación para siempre. Por lo tanto, la variable asociada a esa transformación conserva su valor definido para siempre, es decir, se conserva.
Por ejemplo, la onda plana implica un valor definido de energía, y por lo tanto es invariante bajo desplazamientos temporales. Al tiempo\(t \) = 0, también es invariante bajo\(x\) desplazamientos, lo que corresponde a que representa una partícula con un valor conocido de impulso. Sin embargo, dado que el impulso y la energía son compatibles para una partícula libre, la función de onda representará el mismo valor de impulso en todos los demás momentos. Es decir, si el impulso es definido en\(t \) = 0, será definido en todo momento posterior, y además tendrá el mismo valor. Es así como la conservación del impulso (y por extensión, la conservación de cualquier otra variable compatible con la energía) se expresa en la mecánica cuántica.
Simetrías y Variables
En la física cuántica moderna, el descubrimiento de nuevas simetrías conduce a nuevas variables dinámicas. En los problemas mostramos cómo se produce eso para las simetrías de paridad (\(x \)→-\(x\)), inversión temporal\(t \) →-\(t\)) y conjugación de carga (el intercambio de partículas con antipartículas). Uno de los ejemplos clave de esto fue el desarrollo de la teoría quark de la materia, que vino de la observación de que el intercambio de ciertos grupos de partículas elementales dejó el universo aproximadamente sin cambios, lo que significa que el universo era (aproximadamente) simétrico bajo estos intercambios.
Ondas de materia confinada
El confinamiento de una onda a una región espacial limitada da como resultado un comportamiento bastante peculiar: la onda solo puede encajar cómodamente en la región confinada si la frecuencia de onda, y por lo tanto la energía de partícula asociada, adquiere un conjunto limitado de valores posibles. Este es el origen de la famosa cuantificación de la energía, de la que proviene el “cuántico” en la mecánica cuántica. Exploraremos dos tipos de confinamiento, confinamiento de posición debido a un pozo de energía potencial y confinamiento rotacional debido a que la rotación de un objeto a través de 2\(π\) radianes devuelve el objeto a su orientación original.
Partícula en una caja
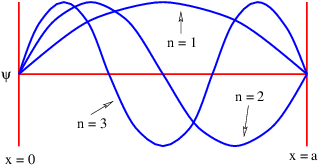
Ahora imaginamos cómo debe comportarse una partícula confinada a una región 0 \(x \)≤ ≤\(a \) en el\(x \) eje. Al igual que con el desplazamiento de una cuerda de guitarra, la función de onda debe ser cero en\(x \) = 0 y\(a\), es decir, en los extremos de la cuerda de guitarra. Una sola onda plana exponencial compleja no puede satisfacer esta condición, ya que | exp [\(i\)(\(kx \)-\(ωt\))] | 2 = 1 en todas partes. Sin embargo, una superposición (con un signo menos) de ondas viajeras hacia la izquierda y hacia la derecha crea una onda estacionaria, en la que la función de onda se separa en una función del espacio sola multiplicada por una función del tiempo solo.
\[ψ = exp[i(kx - ωt)] - exp [i(- kx - ωt)] = 2iexp(- iωt)sin(kx). \label{9.13}\]
Observe que la dependencia del tiempo sigue siendo un exponencial complejo, lo que significa que \(ψ\)| | 2 es independiente del tiempo. Esto asegura que la probabilidad de encontrar la partícula en algún lugar de la caja permanece constante con el tiempo. También significa que el paquete de ondas corresponde a una energía definida\(E \) =\(ℏ\)\(ω\).
Debido a que tomamos una diferencia en lugar de una suma de ondas planas, la condición\(ψ \) = 0 ya está satisfecha en\(x \) = 0. Para satisfacerlo a\(x \) =\(a\), debemos tener\(ka \) =\(nπ\), donde\(n \) = 1\(, \) 2\(, \) 3\(,\)\(…\). Así, el valor absoluto del número de onda debe tomar los valores discretos
\[ nπ- kn = a , n = 1,2,3,.... \label{9.14}\]
(Los números de onda de las dos ondas planas son iguales a más o menos este valor absoluto respectivamente). Esto implica que el valor absoluto del momento de la partícula es π n =\(ℏ\)\(k\) n =\(nπ\)\(ℏ\)\(∕a\), lo que a su vez significa que la energía de la partícula debe ser
\[En = (Π2nc2 + m2c4 )1∕2 = (n2 π2¯h2c2∕a2 + m2c4 )1∕2, \label{9.15}\]
donde\(m \) está la masa de partículas. En el límite no relativista esto se convierte
\[ 2 2 2 2 En = Π-n-= n-π-¯h-- (non-relativistic) 2m 2ma2 \label{9.16} \]
donde hemos bajado la energía de descanso\(mc\) 2 ya que es un desplazamiento constante. En el caso ultra-relativista donde podemos ignorar la masa de partículas, encontramos
\[E = |Π |c = n-π¯hc (zero mass ). n n a \label{9.17}\]
Las formas de las funciones de onda para los tres primeros valores de\(n \) para la partícula en el cuadro se ilustran en la figura 9.2.
En ambos límites la energía toma solo un cierto conjunto de valores posibles. Esto se llama cuantificación de energía y el entero\(n \) se llama el número cuántico de energía. En el límite no relativista la energía es proporcional a\(n\) 2, mientras que en el caso ultrarrelativista la energía es proporcional a\(n\).
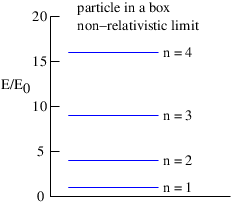
Podemos representar gráficamente los niveles de energía permitidos para la partícula en una caja mediante un diagrama de niveles de energía. Dicho diagrama se muestra en la figura 9.3 para el caso no relativista.
Un aspecto de este problema merece una mirada más cercana. La ecuación (9.13) muestra que la función de onda para este problema es una superposición de dos ondas planas correspondientes a momenta π 1 = +\(ℏ\)\(k \) y π 2 = -\(ℏ\)\(k \) y por lo tanto es una especie de paquete de ondas. Así, la función de onda no es invariante bajo desplazamiento y no corresponde a un valor definido del impulso —el valor absoluto del impulso es definido, pero su signo no lo es. Siguiendo la prescripción de Feynman, la ecuación 9.13} nos dice que la amplitud para que la partícula en la caja tenga momentum +\(ℏ\)\(k \) es exp [\(i\)(\(kx \)-\(ωt\))], mientras que la amplitud para que tenga momentum -\(ℏ\)\(k \) es - exp [\(i\)(-\(kx \) -\(ωt\))]. El cuadrado absoluto de la suma de estas amplitudes nos da la probabilidad relativa de encontrar la partícula en posición\(x\):
\[P(x ) = |2iexp (- iωt) sin(kx )|2 = 4 sin2(kx ). \label{9.18}\]
Cuál de los dos posibles valores del impulso que adquiere la partícula es incognoscible, así como es imposible en principio saber por qué hendidura pasa una partícula en dos rendijas de interferencia. Si se realiza un experimento para medir el momento, entonces la función de onda se cambia irreversiblemente, así como el patrón de interferencia en el problema de dos hendiduras se destruye si la hendidura a través de la cual pasa la partícula se determina inequívocamente.
Penetración de barrera
A diferencia de la situación en la mecánica clásica, la mecánica cuántica permite que la energía\(K \) cinética sea negativa. Esto hace que el impulso π (igual a (2\(mK\)) 1 2 en el caso no relativista) sea imaginario, lo que a su vez da lugar a un número de onda imaginario.
Investiguemos la naturaleza de una ola con un número de onda imaginario. Supongamos que\(k \) =\(iκ \) en una onda plana exponencial compleja, donde\(κ \) es real:
\[ψ = exp[i(kx - ωt)] = exp(- κx - iωt) = exp (- κx )exp(- iωt). \label{9.19}\]
La función de onda no oscila en el espacio cuando\(K \) =\(E \) -\(U < \) 0, sino que crece o decae exponencialmente con\(x\), dependiendo del signo de\(κ\).
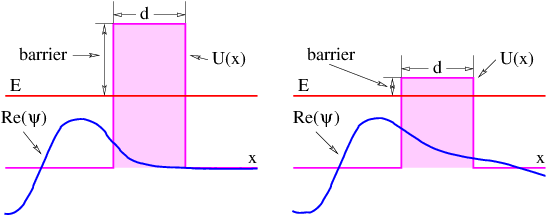
Para una partícula que se mueve hacia la derecha, con positivo\(k \) en la región permitida,\(κ\) resulta ser positiva, y la solución se descompone hacia la derecha. Así, una partícula que incide sobre una barrera de energía potencial desde la izquierda (es decir, mientras se mueve hacia la derecha) tendrá su decaimiento de amplitud de onda en la región clásicamente prohibida, como se ilustra en la figura 9.4. Si esta descomposición es muy rápida, entonces el resultado es casi indistinguible del resultado clásico —la partícula no puede penetrar en gran medida en la región prohibida. Sin embargo, si la descomposición es lenta, entonces hay una probabilidad razonable de encontrar la partícula en la región prohibida. Si la región prohibida es finita en extensión, entonces la amplitud de onda será pequeña, pero distinta de cero en su límite derecho, lo que implica que la partícula tiene una probabilidad finita de pasar completamente por la región prohibida clásica. Este proceso se llama penetración de barrera.
La probabilidad de que una partícula penetre en una barrera es el cuadrado absoluto de la amplitud después de la barrera dividido por el cuadrado de la amplitud antes de la barrera. Así, en el caso de la función de onda ilustrada en la ecuación 9.19}, la probabilidad de penetración es
\[P = |ψ (d)|2∕|ψ(0)|2 = exp(- 2κd) \label{9.20}\]
donde\(d \) está el grosor de la barrera.
La tasa de decaimiento exponencial con\(x \) en la región prohibida está relacionada con lo negativo\(K \) que es en esta región. Desde
\[ Π2 ¯h2k2 ¯h2κ2 - K = U - E = - ----= - -----= -----, 2m 2m 2m \label{9.21} \]
nos encontramos con que
\[ ( )1∕2 κ = 2mB-- ¯h2 \label{9.22} \]
donde la barrera energética potencial es\(B \) ≡-\(K \) =\(U \) -\(E\). Cuanto más pequeño\(B \) es, cuanto más pequeño es\(κ\), lo que resulta en una disminución menos rápida de la función de onda con\(x\). Esto corresponde a una penetración de barrera más fuerte. (Obsérvese que el camino\(B \) está definido, es positivo en regiones prohibidas.)
Si la barrera de energía es muy alta, entonces la decadencia exponencial de la función de onda es muy rápida. En este caso la función de onda va casi a cero en el límite entre las regiones permitidas y prohibidas. Es por ello que especificamos que la función de onda sea cero en las paredes para la partícula en una caja. Estos muros actúan en efecto como barreras de potencial infinitamente alto.
La penetración de barrera es importante en una serie de fenómenos naturales. Ciertos tipos de desintegración radiactiva y la fisión de núcleos pesados se rigen por este proceso.
Momento angular orbital
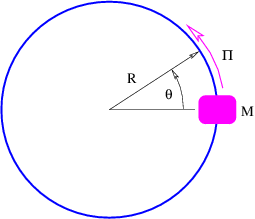
Otro tipo de movimiento de estado enlazado ocurre cuando una partícula está restringida para moverse en un círculo. (Imagine un cordón deslizándose sobre un bucle circular de alambre, como se ilustra en la figura 9.5). Podemos definir\(x \) en este caso como la longitud del camino alrededor del cable y relacionarlo con el ángulo\(θ\):\(x \) =\(Rθ\). Para una ola de avión tenemos
\[ψ = exp[i(kx - ωt)] = exp[i(kR θ - ωt )]. \label{9.23}\]
Esta onda plana difiere de la onda plana normal para el movimiento a lo largo de un eje cartesiano en que debemos tener\(ψ\) (\(θ\)) =\(ψ\) (\(θ \)+ 2\(π\)). Esto sólo puede suceder si la circunferencia del bucle, 2\(πR\), es un número integral de longitudes de onda, es decir, si 2\(πR∕λ \) =\(m \) donde\(m \) es un número entero. Sin embargo, desde 2\(π∕λ \) =\(k\), esta condición se convierte en\(kR \) =\(m\).
Desde π =\(ℏ\)\(k\), la condición anterior se puede escribir π m\(R \) =\(m\)\(ℏ\). La cantidad
\[Lm ≡ ΠmR \label{9.24}\]
se llama el momento angular, lo que lleva a nuestro resultado final,
\[Lm = m ¯h, m = 0,±1, ±2, .... \label{9.25}\]
Vemos que el momento angular sólo puede tomar valores que son múltiplos enteros de\(ℏ\). Esto representa la cuantificación del momento angular, y\(m \) en este caso se llama el número cuántico de momento angular. Tenga en cuenta que este número cuántico difiere del número cuántico de energía para la partícula en la caja en que se permiten valores cero y negativos.
La energía de nuestro cordón en un bucle de alambre se puede expresar en términos del momento angular:
\[ Π2 L2 Em = --m- = ---m-2-. 2M 2M R \label{9.26} \]
Esto significa que el momento angular y la energía son variables compatibles en este caso, lo que significa además que el momento angular es una variable conservada. Así como los valores definidos de impulso lineal están relacionados con la invarianza bajo traslaciones, los valores definidos de momento angular están relacionados con la invarianza bajo rotaciones. Por lo tanto, tenemos
\[invariance under rotation ⇐ ⇒ definite angular momentum \label{9.27}\]
para el momento angular.
Tenemos que abordar brevemente el tema del momento angular en tres dimensiones. El momento angular es en realidad un vector orientado perpendicular al bucle de alambre en el ejemplo que estamos discutiendo. La dirección del vector se define usando una variación en la regla de la derecha: Enrilla tus dedos en la dirección del movimiento de la cuenta alrededor del bucle (¡usando tu mano derecha!). La orientación del vector de momento angular se define por la dirección en la que apunta el pulgar. Esto te dice, por ejemplo, que el momento angular en la figura 9.5 señala fuera de la página.
En mecánica cuántica solo es posible medir simultáneamente el cuadrado de la longitud del vector de momento angular y un componente de este vector. Dos componentes diferentes del momento angular no se pueden medir simultáneamente debido al principio de incertidumbre. Sin embargo, la longitud del vector de momento angular puede medirse simultáneamente con un componente. Así, en la mecánica cuántica, el momento angular se especifica completamente si se conoce la longitud y una componente del vector de momento angular.
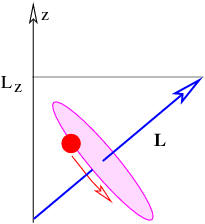
La Figura 9.6 ilustra el vector de momento angular asociado con un cordón que se mueve sobre un bucle de alambre que está inclinado desde la horizontal. También se muestra un\(z \) componente (tomado para ser el componente). Por razones que no podemos explorar aquí, el cuadrado de la longitud del vector de momento angular\(L\) 2 se cuantifica con los siguientes valores:
\[ 2 2 L l = ¯h l(l + 1), l = 0,1,2,.... \label{9.28}\]
Un componente (digamos, el\(z \) componente) del momento angular se cuantifica igual que el momento angular en el caso bidimensional, excepto que\(l \) actúa como límite superior sobre los posibles valores de |\(m\) |. En otras palabras, si el cuadrado de la longitud del vector de momento angular es\(ℏ\) 2\(l\) (\(l \)+ 1), entonces el\(z \) componente puede tomar los valores
\[Lzm = ¯hm, m = - l,- l + 1,...,l - 1, l. \label{9.29}\]
A la cantidad\(l \) se le llama el número cuántico de momento angular, mientras que\(m \) se llama el número cuántico de orientación o magnético, este último por razones históricas.
Momentum Angular
El tipo de momento angular discutido anteriormente está asociado con el movimiento de partículas en órbitas. Sin embargo, resulta que incluso las partículas estacionarias pueden poseer un momento angular. Esto se llama momento angular de giro. El número cuántico de espín\(s \) juega un papel análogo al\(l \) del momento angular de giro, es decir, el cuadrado del vector de momento angular de giro de una partícula es
\[ 2 2 L s = ¯h s(s + 1). \label{9.30}\]
El número cuántico de orientación de espín\(m\) s está relacionado de manera similar con\(s\):
\[Lzs = ¯hms, ms = - s,- s + 1,...,s - 1,s. \label{9.31}\]
El momento angular de giro para una partícula elemental está absolutamente conservado, es decir, nunca puede cambiar. Así, el valor de\(s \) es una propiedad intrínseca de una partícula. La mayor diferencia entre el giro y el momento angular orbital es que el número cuántico de espín puede tomar más valores, es decir,\(s \) = 0\(, \) 1\(∕\) 2\(, \) 1\(, \) 3\(∕\) 2\(, \) 2\(, \) 5\(∕\) 2\(,\)\(…\).
Las partículas con valores de espín entero\(s \) = 0\(, \) 1\(, \) 2\(,\)\(…\) se llaman bosones después del físico indio Satyendra Nath Bose. Las partículas con valores de espín semienteros\(s \) = 1\(∕\)\(∕\) 2\(, \) 3\(∕\) 2\(, \) 5 2\(,\)\(…\) se llaman fermiones después del físico italiano Enrico Fermi. Como veremos más adelante en el curso, los bosones y los fermiones juegan papeles muy diferentes en el universo.
Problemas
- Supongamos que una partícula está representada por la función de onda\(ψ \) = sin (\(kx \)-\(ωt\)) + sin (-\(kx \) -\(ωt\)).
- Utilice la trigonometría para simplificar esta función de onda.
- Calcular la\(x \) y\(t \) dependencia de la probabilidad de encontrar la partícula al cuadrar la función de onda.
- Explique lo que dice este resultado sobre la dependencia temporal de la probabilidad de encontrar la partícula. ¿Tiene sentido esto?
- Repita el problema anterior para una partícula representada por la función de onda\(ψ \) = exp [\(i\)(\(kx \)-\(ωt\))] + exp [\(i\)(-\(kx \) -\(ωt\))].
- Determinar si la función de onda\(ψ\) (\(x\)) = exp (\(iCx\)2) es invariante bajo desplazamiento en el sentido de que la función de onda desplazada difiere de la función de onda original por solo un factor de fase.
- Así como la invarianza bajo la sustitución\(x \) →\(x \) +\(D \) se asocia con el impulso, la invarianza bajo la sustitución\(x \) →-\(x \) se asocia con una variable mecánica cuántica llamada paridad, denotada\(P\). Sin embargo, a diferencia del impulso, que puede tomar cualquier valor numérico, la paridad solo puede tomar dos valores posibles, ± 1. La paridad de una función de onda\(ψ\) (\(x\)) es +1 if\(ψ\) (-\(x\)) =\(ψ\) (\(x\)), mientras que la paridad es - 1 if\(ψ\) (-\(x\)) = -\(ψ\) (\(x\)). Si\(ψ\) (\(x\)) no satisface ninguna de estas condiciones, entonces no tiene un valor definido de paridad.
- ¿Cuál es la paridad de\(ψ \) = sin (\(kx\))? De\(ψ \) = cos (\(kx\))? La cantidad\(k \) es una constante.
- Es\(ψ\) (\(x\)) = cos (\(kx\)) invariante bajo la sustitución\(x \) =\(x \) +\(D \) para todos los valores posibles de\(D\)? ¿Esta función de onda tiene un valor definido del impulso?
- Demostrar que una función de onda con un valor definido del impulso no tiene un valor definido de paridad. ¿Las variables de impulso y paridad son compatibles?
- Al darse cuenta de que cos (\(kx \)-\(ωt\)) se puede escribir en términos de funciones exponenciales complejas, dar una interpretación física del significado de la función de onda coseno anterior. En particular, ¿cuáles son los posibles valores del impulso y la energía de la partícula asociada?
- La operación de inversión de tiempo\(T \) realiza la sustitución\(t \) →-\(t\). Similar a la paridad, la inversión de tiempo solo puede tomar valores ± 1. ¿La simetría de una onda funciona bajo inversión de tiempo, es decir,\(ψ\) (-\(t\)) =\(ψ\) (\(t\)), consistente con un valor definido de la energía? Pista: Cualquier función de onda correspondiente a un valor definido de energía\(E \) debe tener la forma\(ψ \) =\(A\) exp (-\(iEt∕\)\(ℏ\)) donde no\(A \) es una función del tiempo\(t\). (¿Por qué?)
- La operación\(C \) toma el complejo conjugado de la función de onda, es decir, realiza la sustitución\(i \) →-\(i\). En la mecánica cuántica moderna esto corresponde a partículas y antipartículas intercambiables, y se llama conjugación de carga. ¿Qué le hace la operación combinada CPT a una onda plana compleja, es decir, una con vector de onda definido y frecuencia?
- Hacer un diagrama de nivel de energía para el caso de una partícula sin masa en una caja.
- Comparar | π | para el estado fundamental de una partícula no relativista en una caja de tamaño\(a \) con Δπ obtenido del principio de incertidumbre en esta situación. Pista: ¿Qué deberías tomar para Δ\(x\)?
- Imagina que una mesa de billar tiene un borde infinitamente alto a su alrededor. Para este problema supongamos que\(ℏ\) = 1 kg m 2 s - 1.
- Si la mesa mide 1\(.\) 5 m de largo y si la masa de una bola de billar es\(M \) = 0\(.\) 5 kg, ¿cuál es la energía más baja o de estado fundamental de la bola de billar? Pista: A pesar de que la mesa de billar es bidimensional, trata esto como un problema unidimensional. También, tratar el problema de manera no relativista e ignorar la contribución de la energía de descanso a la energía total.
- La energía requerida para levantar la pelota sobre un borde de altura\(H \) contra la gravedad es\(U \) =\(MgH \) donde\(g \) = 9\(.\) 8 m s - 2. ¿Qué altura de llanta hace que la energía potencial gravitacional sea igual a la energía del estado del suelo de la bola de billar calculada anteriormente?
- Si la llanta es en realidad dos veces más alta que la calculada anteriormente pero solo tiene 0\(.\) 1 m de grosor, determine la probabilidad de que la bola penetre en la llanta.
Figura 9.7: Parte real de la función de onda\(ψ\), correspondiente a una energía total fija\(E\), que ocurre en una región de energía potencial espacialmente variable\(U\) (\(x\)). Observe cómo\(λ \) cambia la longitud de onda a medida que\(U \) cambia la energía cinética\(K \) =\(E \) -.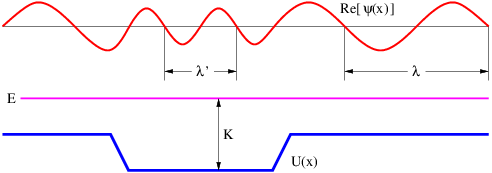
_____________________________________
- La parte real de la función de onda de una partícula con energía positiva\(E\) que pasa por una región de energía potencial negativa se muestra en la figura 9.7.
- Si la energía total es definitivamente\(E\), ¿cuál es la dependencia de esta función de onda en el tiempo?
- ¿La función de onda es invariante bajo desplazamiento en el espacio en este caso? ¿Por qué o por qué no?
- ¿Esta función de onda corresponde a un valor definido de impulso? ¿Por qué o por qué no?
- ¿El impulso es compatible con la energía en este caso? ¿Por qué o por qué no?
- Suponiendo de nuevo que\(ℏ\) = 1 kg m 2 s - 1, ¿cuáles son las velocidades posibles de un tren de juguete de masa 3 kg corriendo alrededor de una vía circular de radio 0\(.\) 8 m?
- Si una partícula de masa cero que se desliza alrededor de un bucle circular de radio\(R \) puede tomar momentos angulares\(L\) m =\(m\)\(ℏ\) donde\(m \) es un entero, ¿cuáles son las posibles energías cinéticas de la partícula? Pista: Recuerda que\(L \) = π\(R\).
Capítulo 10 Dinámica de Partículas Múltiples
Hasta el momento solo hemos considerado la dinámica de una sola partícula sujeta a una energía potencial impuesta externamente. La partícula no tiene forma de influir en este agente externo. En el mundo real las partículas interactúan entre sí. En este capítulo aprendemos cómo sucede esto.
Primero reescribimos la segunda ley de Newton en términos de impulso. Esto es útil en la posterior consideración de la tercera ley de Newton, que conduce al principio de la conservación del impulso. Luego se estudian las colisiones entre partículas y el comportamiento de cohetes y cintas transportadoras como aplicaciones de las leyes de conservación a más de una partícula.
Momentum y la Segunda Ley de Newton
Hasta este punto hemos declarado la segunda ley de Newton en su forma convencional,\(F\) =\(m\)\(a\). Sin embargo, en el caso no relativista\(m\)\(a\) =\(md\)\(u\)\(∕dt \) =\(d\) (\(m\)\(u\))\(∕dt\), por lo que también podemos escribir la segunda ley de Newton como
\[F = dp- (Newton ’s second law ) dt \label{10.1}\]
donde\(p\) =\(m\)\(u\) es el impulso cinético no relativista. Esta forma de la segunda ley de Newton está en realidad más cerca de la declaración original de Newton sobre la ley. También tiene la ventaja de que es correcta incluso en el caso relativista cuando la definición relativista de impulso cinético,\(p\) =\(m\)\(u\)\(∕\) (1 -\(u\) 2\(∕c\) 2) 1 2 (como se definió anteriormente), se sustituye.
Tercera Ley de Newton
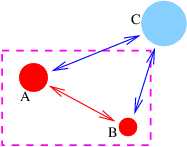
La tercera ley de Newton establece que si la partícula A ejerce una fuerza\(F\) sobre la partícula B, entonces la partícula B ejerce una fuerza,\(F\) sobre la partícula A. La tercera ley de Newton permite aplicar la segunda ley de Newton a los sistemas de partículas sin considerar las interacciones detalladas entre partículas dentro del sistema. Por ejemplo, si definimos (arbitrariamente) el sistema en la figura 10.1 como las partículas A y B dentro de las líneas discontinuas, entonces podemos dividir las fuerzas que actúan sobre estas partículas en partes internas y externas,
\[FA = FA -internal + FA -external = dpA-, dt \label{10.2}\]\[FB = FB -internal + FB -external = dpB-. dt \label{10.3}\]
Al sumar estas ecuaciones, la fuerza neta\(F\) neta es igual a
\[ d- FA -internal + FA -external + FB -internal + FB -external = dt(pA + pB ). \label{10.4}\]
No obstante, las interacciones internas en este caso son A actuando sobre B y B actuando sobre A. Estas fuerzas son iguales en magnitud pero opuestas en dirección, por lo que cancelan, dejándonos con la fuerza neta igual a la suma de las partes externas,\(F\) net =\(F\) A - externo +\(F\) B - externo. Las fuerzas externas en la figura 10.1 son la fuerza de C sobre A y la fuerza de C sobre B. Definiendo el momento cinético total del sistema como la suma de los momentos A y B,\(p\) tot =\(p\) A +\(p\) B, la ecuación anterior se convierte
\[ dptot Fnet = -----, dt \label{10.5} \]
que se parece a la segunda ley de Newton para una sola partícula, salvo que ahora se aplica al sistema de partículas (A y B en el presente caso) en su conjunto. Este argumento generaliza fácilmente a cualquier número de partículas dentro y fuera del sistema. Así, por ejemplo, a pesar de que un balón de fútbol consta de miles de millones de átomos, estamos seguros de que las fuerzas entre átomos dentro del balón de fútbol se cancelan, y la trayectoria del balón en su conjunto está determinada únicamente por fuerzas externas como la gravedad, la resistencia al viento, la fricción con el suelo y las patadas del fútbol jugadores.
Recuerda que para que dos fuerzas sean una tercera pareja de ley, tienen que estar actuando sobre diferentes partículas. Además, si un miembro del par es la fuerza de la partícula A que actúa sobre la partícula B, entonces el otro debe ser la fuerza de la partícula B que actúa sobre la partícula A. Un contraejemplo sería la gravedad y la fuerza normal ascendente que actúa sobre una masa sentada sobre una mesa; estas fuerzas son iguales y opuestas en el caso estacionario , sino actuar sobre el mismo objeto, y por lo tanto no constituyen un tercer par de leyes. No obstante, la fuerza normal ascendente de la tabla sobre la masa y la fuerza normal descendente de la masa sobre la mesa serían un tercer par de leyes.
Conservación del Momentum
Si todas las fuerzas externas en un sistema son cero, entonces la ecuación 10.5} se reduce a
\[ptot = const (isolated system ). \label{10.6}\]
Un sistema de partículas sin fuerzas externas que actúen sobre él se llama aislado. La tercera ley de Newton nos dice así que el impulso cinético de un sistema aislado no cambia con el tiempo. A esta ley se le llama la conservación del impulso.
Colisiones
Consideremos ahora la situación en la que dos partículas chocan entre sí. Puede haber varios resultados de esta colisión, de los cuales estudiaremos dos:
- Las dos partículas chocan elásticamente, en esencia rebotando una de la otra.
- Las dos partículas se pegan entre sí, dando como resultado la producción de una sola partícula, o una sola partícula se rompe en dos partículas. Se trata de procesos inelásticos.
En ambos casos se conserva la energía y el impulso. Suponemos que las fuerzas que actúan entre las partículas son de corto alcance, de modo que excepto en el instante de colisión, no necesitamos preocuparnos por la energía potencial o el impulso potencial —toda la energía está en forma de reposo más energía cinética excepto en este corto intervalo, y todos los momentos son momentos cinéticos.
Debido al principio de relatividad, somos libres de considerar colisiones en cualquier marco de referencia conveniente. Luego podemos transformar los resultados a cualquier marco de referencia que queramos. En términos generales, el marco de referencia más conveniente a considerar es aquel en el que el impulso total de las dos partículas es cero. En aras de la simplicidad, solo consideramos colisiones en una dimensión.
Colisiones Elásticas
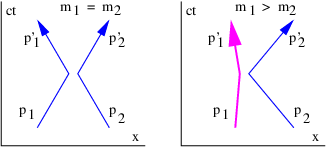
Supongamos que una partícula con masa\(m\) \(u\)1 y velocidad inicial 1 en el centro del marco de momento, es decir, el marco de referencia en el que el momento total es cero, choca elásticamente con otra partícula de masa \(m\)2 con velocidad inicial\(u\) 2. Los momentos de las dos partículas son
\[p = ----m1u1------ p = ----m2u2------. 1 (1 - u21∕c2)1∕2 2 (1 - u22∕c2)1∕2 \label{10.7}\]
En el centro del marco de impulso debemos tener
\[p1 = - p2. \label{10.8}\]
La Figura 10.2 muestra lo que sucede cuando estas dos partículas chocan. La primera partícula adquiere impulso\(p\) 1′ mientras que la segunda adquiere impulso\(p\) 2′. La conservación del impulso nos dice que el impulso total después de la colisión es el mismo que antes de la colisión, es decir, cero, entonces
\[ ′ ′ p1 = - p2. \label{10.9}\]
En el marco del centro del momentum sabemos que |\(p\) 1 | = |\(p\) 2 | y sabemos que los dos vectores de impulso apuntan en direcciones opuestas. De manera similar, |\(p\) 1 ′| = |\(p\) 2 ′|. Sin embargo, todavía no sabemos cómo se relaciona\(p\) 1 ′ con\(p\) 1. Conservación de la energía,
\[E1 + E2 = E ′1 + E ′2, \label{10.10}\]
nos da esta información. Observe que si\(p\) 1 ′ = -\(p\) 1, entonces\(E\) 1 ′ 2 =\(p\) 1 ′ 2 \(c\)2 +\(m\) 1 2\(c\) 4 =\(p\) 1 2\(c\) 2 +\(m\) 1 2\(c\) 4 =\(E\) 1 2. Asumiendo energías positivas, por lo tanto tenemos\(E\) 1 ′ =\(E\) 1. Si\(p\) 2 ′ = -\(p\) 2, entonces podemos inferir de manera similar que\(E\) 2 ′ =\(E\) 2. Si se cumplen estas condiciones, entonces también lo es la ecuación 10.10}. Por lo tanto, una solución completa al problema es
\[ ′ ′ p1 = - p 1 = - p2 = p2 ≡ p \label{10.11}\]
y
\[E = E ′ = (p2c2 + m2 c4)1∕2 E = E ′ = (p2c2 + m2 c4)1∕2. 1 1 1 2 2 2 \label{10.12}\]
En otras palabras, las partículas simplemente intercambian momentos.
El panel izquierdo de la figura 10.2 muestra lo que sucede en una colisión cuando las masas de las dos partículas colisionantes son iguales. Si\(m\) 1 =\(m\) 2, entonces las velocidades de entrada y salida de las dos partículas son las mismas, como lo indican las pendientes inversas de las líneas mundiales. Por otro lado, si\(m\) 1\(> m\) 2, entonces la velocidad de la partícula 2 es mayor que la velocidad de la partícula 1, como se ilustra en el panel derecho de la figura 10.2.
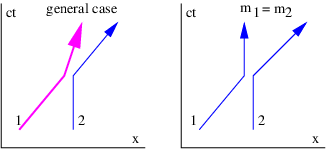
Supongamos que deseamos ver los resultados de una colisión elástica en un marco de referencia en el que la partícula 2 es inicialmente estacionaria. Todo lo que tenemos que hacer es transformar las velocidades en un marco de referencia que se mueve con la velocidad inicial de la partícula 2, como se ilustra en la figura 10.3. Esto lo hacemos sumando relativisticamente\(U \) = -\(u\) 2 a cada velocidad. (Tenga en cuenta que la velocidad\(U \) del cuadro en movimiento es positiva ya que\(u\) 2 es negativa). Usando la fórmula relativista de traducción de velocidad, encontramos que
\[ ′ ′ v1 = --u1 +-U--- v′ = --u1-+-U--- v′ = --u2 +-U--- 1 + u1U∕c2 1 1 + u′1U ∕c2 2 1 + u ′2U∕c2 \label{10.13} \]
donde\(u\) \(u\)1 , 1′,\(u\) \(u\)2 y 2′ indican velocidades en el marco de referencia original, centro de momento y\(v\) \(v\)1 , 1′, etc., indican velocidades en el fotograma transformado.
En el caso especial donde las masas de las dos partículas son iguales entre sí, tenemos\(v\) 1 = 2\(U∕\) (1 +\(U\) 2\(∕c\) 2),\(v\) 1 ′ = 0, y \(v\)2′ = 2\(U∕\) (1 +\(U\) 2\(∕c\) 2) =\(v\) 1. Así, cuando las masas son iguales, las partículas simplemente intercambian velocidades.
Si las velocidades son no relativistas, entonces la ley de transformación galileana más simple\(v \) =\(u \) + se\(U \) puede usar en lugar de las ecuaciones relativistas invocadas anteriormente.
Colisiones inelásticas
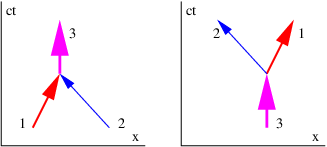
Una colisión inelástica es aquella en la que las partículas que salen de la colisión no son las mismas que las partículas que entran en ella. Las colisiones inelásticas conservan tanto el impulso total como la energía tal como lo hacen las colisiones elásticas. Sin embargo, a diferencia de las colisiones elásticas, las colisiones inelásticas generalmente no conservan la energía cinética total de las partículas, ya que generalmente se crea o destruye alguna energía de reposo.
La Figura 10.4 muestra los bloques de construcción fundamentales de las colisiones inelásticas. Podemos considerar que incluso las colisiones inelásticas más complejas están compuestas por compuestos de solo dos procesos, la creación de una partícula a partir de dos, y la desintegración de una partícula en dos.
Consideremos cada uno de estos en el centro del marco de impulso. En ambos casos la partícula única debe ser estacionaria en este marco ya que lleva el impulso total del sistema, que tiene que ser cero. Por conservación del momento, si la partícula 1 en el panel izquierdo de la figura 10.4 tiene impulso\(p\), entonces el impulso de la partícula 2 es -\(p\). Si las dos partículas tienen masas\(m\) 1 y\(m\) 2, entonces sus energías son\(E\) 1 = (\(p\)2\(c\) 2 +\(m\) 1 2\(c\) 4) 1 2 y\(E\) 2 = (\(p\)2\(c\) 2 + \(m\)2 2\(c\) 4) 1 2. La energía de la partícula 3 es, por lo tanto,\(E\) 3 =\(E\) 1 +\(E\) 2, y como está en reposo, toda su energía está en forma de “\(mc\)2” o energía de reposo, y así la masa de esta partícula es
\[m3 = (E1 + E2)∕c2 (center of momentum frame ) 2 2 2 1∕2 2 2 21∕2 = (p ∕c + m 1) + (p ∕c + m 2) = m1 [1 + p2∕(m21c2)]1∕2 + m2 [1 + p2∕(m22c2)]1∕2. \label{10.14} \]
La última línea de la ecuación anterior muestra que\(m\) 3\(> m\) 1 +\(m\) 2 porque está en la forma\(m\) 1\(A \) +\(m\) 2 \(B \)donde ambos\(A \) y\(B \) son mayores que uno. Así, la energía de reposo se crea en la cantidad Δ\(E\) rest = (\(m\)3 -\(m\) 1 -\(m\) 2)\(c\) 2.
En realidad, es fácil calcular la masa de la partícula 3 en el caso anterior a partir de cualquier marco de referencia siempre y cuando se conozcan los momentos y energías de las partículas 1 y 2 en este marco. Por conservación de energía e impulso,\(E\) 3 =\(E\) 1 +\(E\) 2 y\(p\) 3 =\(p\) 1 +\(p\) 2. Además,\(E\) 3 2 =\(p\) 3 2\(c\) 2 +\(m\) 3 2\(c\) 4, así que podemos resolver para\(m\) 3:
\[m = [(E + E )2∕c4 - (p + p ) ⋅ (p + p )∕c2]1∕2 (any frame ). 3 1 2 1 2 1 2 \label{10.15}\]
El panel derecho de la figura 10.4 muestra el proceso de descomposición de las partículas. Esto es solo lo inverso del proceso de creación de partículas, y todo el análisis que hemos hecho para la creación es válido para la descomposición de las partículas excepto que la energía de reposo se convierte en energía cinética en lugar de viceversa.
Cohetes y Cintas Transportadoras
Normalmente cuando definimos un sistema al que se va a aplicar la segunda ley de Newton, el sistema se cierra en el sentido de que la masa no puede entrar o salir del sistema. No obstante, a veces es conveniente trabajar con sistemas abiertos para los cuales esto no es cierto. El ejemplo clásico es el cohete, donde los gases de escape salen del sistema, disminuyendo así la masa del cohete con el tiempo.
Los sistemas abiertos pueden analizarse si se considera que el impulso es una cantidad que se contabiliza tanto como el dinero se contabiliza en una cuenta bancaria. La cuenta bancaria puede cambiar de tres maneras: el dinero se puede depositar en la cuenta, se puede retirar de la cuenta, y el monto puede crecer o reducirse como consecuencia de pagos de intereses o comisiones. De igual manera, la cantidad de impulso en un sistema puede cambiar como resultado de la entrada de masa al sistema, la masa que sale del sistema y las fuerzas que actúan sobre el sistema. La tasa de tiempo de cambio de impulso en un sistema es por lo tanto
\[ ( ) ( ) dp dp dp dt-= F + dt- - dt- , in out \label{10.16} \]
donde\(F \) está la fuerza neta en el sistema, (\(dp∕dt\)) in es el impulso por unidad de tiempo agregado por la masa que ingresa al sistema, y (\(dp∕dt\)) out es la cantidad perdida por unidad de tiempo por masa que sale del sistema. En el caso no relativista, (\(dp∕dt\)) in = in (\(dm∕dt\))\(u\) in y () out = out (\(dp∕dt\))\(u\) out (\(dm∕dt\)) out , donde (\(dm∕dt\)) in es la masa que ingresa al sistema por unidad de tiempo con velocidad\(u\) de entrada y (\(dm∕dt\)) salida es la masa por unidad de tiempo que sale del sistema con velocidad\(u\) fuera.
Para velocidades no relativistas, el impulso del sistema puede escribirse como\(p \) =\(mu \) para que
\[dp-= dm-u + m du-. dt dt dt \label{10.17}\]
Para completar el análisis, necesitamos una contabilidad de la masa que ingresa y sale del sistema:
\[ ( ) ( ) dm-- dm-- dm-- dt = dt - dt . in out \label{10.18} \]
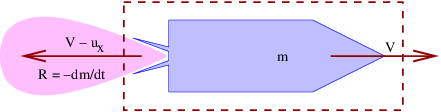
Veamos cómo aplicar esto a un cohete para el que todas las velocidades son no relativistas. Como indica la figura 10.5, un cohete arroja una corriente de gases de escape. El sistema está definido por la caja discontinua e incluye el cohete y la parte del gas de escape dentro de la caja. La reacción al impulso arrastrado en esta corriente de gas es lo que hace que el cohete acelere. Observamos que (\(dm∕dt\)) in = 0 ya que ninguna masa está entrando al sistema, y (\(dm∕dt\)) out =\(R\), la velocidad a la que la masa es expulsada por el cohete en forma de gas de escape. Se supone que el cohete se mueve hacia la derecha a velocidad\(V \) y el gas es expulsado a una velocidad\(u\) x relativa al cohete, lo que significa que su velocidad real después de la expulsión es\(V \) -\(u\) x. Llamamos\(u\) x la velocidad de escape. Observe que\(V \) -\(u\) x puede ser positiva o negativa, dependiendo de qué tan grande\(V\) sea.
Equiparando la masa del cohete con la masa del sistema, encontramos que\(R \) = -\(dm∕dt\). La ecuación de balance de impulso 10.16} se convierte en\(dp∕dt \) = - (\(V \)-\(u\) x)\(R\). La fuerza sobre el cohete es en realidad cero, por lo que el término de fuerza no entra en la ecuación del balance de impulso. Esto no es intuitivo, porque estamos acostumbrados a que la aceleración sea el resultado de una fuerza. Sin embargo, nada, incluido el gas expulsado, en realidad está presionando al sistema, por lo que de hecho debemos concluir que no hay fuerza —todo el cambio en el impulso del sistema surge de la expulsión de gas con el impulso opuesto. 1
Por último, vemos que\(dp∕dt \) = (\(dm∕dt\))\(V \) +\(m\) (\(dV∕dt\)) = -\(RV \) +\(m\) (\(dV∕dt\)). Equiparar esto con los resultados del cálculo del balance de impulso nos da -\(RV \) +\(m\) (\(dV∕dt\)) = - (\(V \)-\(u\) x)\(R\). Resolviendo para los\(dV∕dt \) resultados de aceleración en
\[dV- = uxR-- (rocket acceleration). dt m \label{10.19}\]
Así, la aceleración del cohete depende de la velocidad de escape del gas expulsado, la velocidad a la que se está expulsando el gas y la masa del cohete.
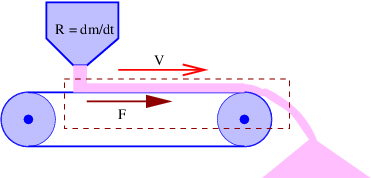
La Figura 10.6 ilustra otro tipo de problema de sistema abierto. Una tolva arroja arena sobre una cinta transportadora a razón de\(R \) kilogramos por segundo. La cinta transportadora se mueve hacia la derecha a una velocidad (no relativista)\(V \) y la arena se descarga al final. ¿Qué fuerza\(F \) se necesita para mantener la cinta transportadora en movimiento a una velocidad constante, asumiendo que el mecanismo de la cinta transportadora en sí no tiene fricción? En este caso (\(dm∕dt\)) in = (\(dm∕dt\)) out =\(R\). Además, dado que el sistema delineado por la línea discontinua se encuentra en estado estacionario,\(dp∕dt \) = 0.
La clave para entender este problema es que la arena ingresa al sistema con velocidad horizontal cero, pero sale del sistema con la velocidad horizontal de la cinta transportadora,\(V \). La ecuación del balance de impulso es así
\[0 = F - VR \label{10.20}\]
y la fuerza es
\[F = VR (force on conveyor belt). \label{10.21}\]
Esta fuerza sirve para acelerar la arena hasta la velocidad de la cinta transportadora.
Problemas
- Imagínese un bloque de masa\(M \) descansando sobre una placa bajo la influencia de la gravedad, como se muestra en la figura 10.7.
- Determinar la fuerza de la placa sobre el bloque,\(N\) b, y la fuerza del bloque sobre la placa,\(N\) p.
- Indique cuál de las tres fuerzas\(M\)\(g\),,\(N\) b y\(N\) p, forman un tercer par de leyes de Newton.
Figura 10.7: Bloque de masa\(M \) sujeto a fuerza gravitacional\(M\)\(g\) mientras descansa sobre una placa. La fuerza del bloque sobre la placa es\(N\) p mientras que la fuerza de la placa sobre el bloque es\(N\) b.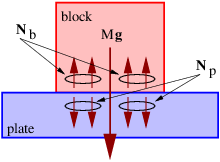
_____________________________________
- Repita el problema anterior asumiendo que el bloque y la placa están en un elevador acelerando hacia arriba con aceleración\(a\).
- Enderezar el malentendido de la tercera ley de Newton implícita en la pregunta “Si la fuerza del caballo en el carro es igual a la fuerza del carro sobre el caballo, ¿por qué algo va a alguna parte alguna vez”? Examine en particular las condiciones bajo las cuales se acelera el sistema de carros de caballos.
- Un barco empujador (masa\(M\)) en el Mississippi está empujando dos barcazas (cada masa\(m\)) a una velocidad constante como se muestra en la figura 10.8. Cada barcaza está sujeta a una fuerza de arrastre por el agua de\(F\) B. Considere solo los componentes de fuerza horizontal en lo siguiente.
- ¿Cuál es la fuerza horizontal total del agua en el sistema de barcaza-barco? Explique.
- ¿Cuál es la dirección y magnitud de la fuerza del barco empujador sobre la barcaza 1? Explique.
Figura 10.8: Barcazas siendo empujadas por un bote empujador en el Mississippi. Cada barcaza experimenta una fuerza de arrastre\(F\) b.
_____________________________________
- Un tren con un motor de masa\(M \) y 2 vagones de carga, cada uno de masa\(m\), está acelerando hacia la derecha con aceleración\(a \) sobre una vía horizontal como se muestra en la figura 10.9. Supongamos que los dos vagones de carga ruedan con una fricción insignificante. Considere solo los componentes de fuerza horizontal a continuación.
- Encuentra la dirección y magnitud de la fuerza de los rieles en el motor y especifica el sistema al que se aplica la segunda ley de Newton.
- Encuentre la dirección y magnitud de la fuerza del motor en el primer automóvil y especifique el sistema al que se aplica la segunda ley de Newton.
- Encuentre la dirección y magnitud de la fuerza del primer automóvil en el segundo automóvil y especifique el sistema al que se aplica la segunda ley de Newton.
- Encuentra la dirección y magnitud de la fuerza del segundo carro sobre el primer auto y especifica la ley utilizada para obtener esta fuerza.
Figura 10.9: Un motor y dos vagones de carga acelerando hacia la derecha.
_____________________________________
- Un automóvil y un remolque están descendiendo una colina como se muestra en la figura 10.10. Supongamos que el remolque rueda sin fricción y que la fricción del aire puede ser ignorada. Considerar solo fuerzas paralelas a la superficie de la carretera.
- Calcule la fuerza de la carretera sobre el automóvil si el sistema de autoremolque que se muestra en la figura 10.10 se mueve cuesta abajo a velocidad constante.
- Calcular la fuerza del tráiler sobre el automóvil en las condiciones anteriores.
- Si el conductor quita el pie del freno y deja que el auto cosione sin fricciones, vuelva a calcular la fuerza del remolque sobre el automóvil.
Figura 10.10: Un automóvil y un tráiler bajando una colina.
_____________________________________
- Considera una colisión elástica unidimensional entre partículas de masas\(m\) 1 y\(m\) 2. Si la partícula 2 es inicialmente estacionaria, ¿qué rango de valores debe tener\(m\) 1\(∕m\) 2 para que la partícula inicial rebote hacia atrás a lo largo de su pista inicial después de la colisión? (Hacer este problema de manera no relativista.)
- Un pión estacionario (masa\(M\)) se descompone en un muón (masa\(m < M\)) y un neutrino (sin masa).
- ¿Cuál es el impulso (completamente relativista) del muón después de la decadencia?
- ¿Cuál es la energía del neutrino?
- En una colisión elástica vista en el centro del marco de momento, la energía de cada partícula se conserva individualmente. ¿Es esto cierto para el mismo proceso visto desde un marco de referencia en el que una de las partículas es inicialmente estacionaria?
- Una sonda espacial se acerca a un planeta en la\(x \) dirección -, se curva a su alrededor bajo la influencia de la poderosa gravedad del planeta (una fuerza conservadora) y retrocede del planeta en la\(x \) dirección +, como se ve en la figura 10.11. El planeta se mueve en la\(x \) dirección + a velocidad\(V \), mientras que la sonda espacial se mueve inicialmente en la\(x \) dirección - a la velocidad\(u\) 1. ¿Cuál es su velocidad\(u\) 2 en la\(x \) dirección + después de este acercamiento cercano al planeta? Tratar este problema de manera no relativista. Pista: Primero transforma al marco del centro de masa en el que el planeta es esencialmente estacionario. Calcular la interacción entre la sonda y el planeta en este marco. Después transforma de nuevo al marco de referencia original. Supongamos que la masa de la sonda es insignificante en comparación con la del planeta.
Figura 10.11: Una sonda espacial se acerca a un planeta, se curva a su alrededor y se dirige en dirección opuesta.
_____________________________________
- Dos asteroides, cada uno con masa 10 10 kg y velocidad inicial 10 5 m s - 1, chocan de frente. Todo el desorden se conforma en una gran masa. ¿Cuánta masa de descanso (energía de descanso dividida por\(c\) 2) se crea?
- Dos objetos iguales, ambos con masa\(m\), chocan y se pegan entre sí. Antes de la colisión, una masa está estacionaria y la otra se mueve a velocidad\(v\). A continuación, supongamos que las velocidades son completamente relativistas.
- Calcular el impulso total y la energía (incluida la energía de reposo) de las dos masas antes de la colisión.
- Calcular la masa\(M \) del sistema combinado después de la colisión, teniendo en cuenta la conversión de energía en masa.
- Explique cualitativamente por qué un bombero necesita empujar hacia adelante una manguera contra incendios para mantenerla estacionaria. Consejo: El agua fluye más rápido después de que sale de la boquilla de la manguera que antes.
- Resolver ecuación 10.19} para\(V \) como una función de\(m\), asumiendo que\(V \) = 0 y\(m \) =\(m\) 0 at\(t \) = 0. Pista: Desde\(R \) = -\(dm∕dt\), tenemos\(R∕m \) = -\(d\) ln (\(m\))\(∕dt\).
- }
- Las botellas se llenan con refresco en una planta embotelladora como se muestra en la figura 10.12. Las botellas se asientan en una báscula que se utiliza para determinar cuándo cerrar el flujo de refresco. Si la masa deseada de la botella más refresco después del llenado es\(M\), ¿qué peso debe leer la báscula cuando la botella está llena? La velocidad a la que se agrega masa a la botella es\(R \) y su velocidad de entrada a la botella es\(V \).
Figura 10.12: Una botella que se llena con refresco a una tasa\(R\). El líquido entra a la botella con velocidad\(V \).
_____________________________________
- Una sonda espacial interestelar tiene área frontal\(A\), masa inicial\(M\) 0 y velocidad inicial\(V\) 0, que es no relativista. El tenue gas entre las estrellas tiene densidad de masa\(ρ\). Estas moléculas de gas se adhieren a la sonda cuando la golpean. Encuentra la aceleración de la sonda. Pista: En un marco de referencia en el que el gas está estacionario, ¿el momento de la sonda espacial cambia con el tiempo? ¿Su masa?
- Un haz de luz con potencia\(J \) golpea una placa que se orienta normalmente al haz. Calcular la fuerza requerida para mantener la placa en su lugar si
- la placa absorbe completamente la luz, y
- la placa refleja completamente la luz.
Pista: Los fotones son sin masa, por lo que el impulso de un fotón con energía lo\(E \) es\(E∕c\). Así, el impulso por unidad de tiempo que golpea la placa es\(J∕c\).
- Encuentra la aceleración de un cohete cuando el “gas” de escape es en realidad un rayo láser de potencia\(J\). Supongamos que el cohete se mueve a velocidades no relativistas y que la disminución de masa debido a la pérdida de energía en el rayo láser es insignificante.
Capítulo 11 Dinámica Rotacional
Ya hemos visto el tratamiento mecánico cuántico del momento angular y la dinámica rotacional. En esta sección estudiamos estos temas en un contexto clásico, no relativista. Primero definimos los conceptos de torque y momento angular para entender el movimiento orbital de una sola partícula. A continuación examinamos dos partículas en movimiento arbitrario y aprendemos cómo la energía cinética y el momento angular se dividen entre componentes orbitales e internos. Dos partículas fijadas a los extremos de una varilla de luz constituyen una mancuerna, que sirve como prototipo para la rotación de cuerpos rígidos. Entonces vemos cómo lo que aprendimos para dos partículas se extiende a un número arbitrario de partículas. Finalmente, exploramos la física de las estructuras en equilibrio estático.
Antes de comenzar, necesitamos extender nuestro conocimiento de vectores al producto cruzado.
Tutorial — Productos cruzados
Hay dos formas de multiplicar dos vectores juntos, el producto punto y el producto cruzado. Ya hemos estudiado el producto punto de dos vectores, lo que da como resultado un número escalar o único.
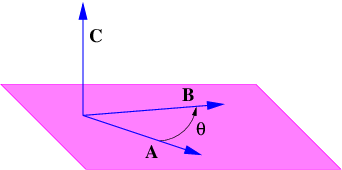
El producto cruzado de dos vectores da como resultado un tercer vector, y se escribe simbólicamente de la siguiente manera:
\[C = A × B. \label{11.1}\]
Como se ilustra en la figura 11.1, el producto cruzado de dos vectores es perpendicular al plano definido por estos vectores. Sin embargo, esto no nos dice si el vector resultante en la figura 11.1 apunta hacia arriba fuera del plano o hacia abajo. Esta ambigüedad se resuelve usando la regla de la derecha:
- Apunte los dedos no curvados de tu mano derecha a lo largo de la dirección del primer vector\(A\).
- Gira tu brazo hasta que puedas curvar tus dedos en la dirección del segundo vector\(B\).
- Su pulgar estirado ahora apunta en la dirección del vector de producto cruzado\(C\).
La magnitud del producto cruzado viene dada por
\[|C | = |A ||B |sin(θ), \label{11.2}\]
donde |\(A\) | y |\(B\) | son las magnitudes de\(A\) y\(B\), y\(θ \) es el ángulo entre estos dos vectores. Obsérvese que la magnitud del producto cruzado es cero cuando los vectores son paralelos o antiparalelos, y máxima cuando son perpendiculares. Esto contrasta con el producto punto, que es máximo para vectores paralelos y cero para vectores perpendiculares.
Observe que el producto cruzado no conmuta, es decir, el orden de los vectores es importante. En particular, es fácil mostrar usando la regla de la derecha que
\[A × B = - B × A. \label{11.3}\]
Una forma alternativa de calcular el producto cruzado es más útil cuando los dos vectores se expresan en términos de componentes, i. e.,\(A\) = (\(A\)x\(,A\) y\(.A\) z) y\(B\) = (\(B\) x\(,B\) y\(,B\) z):
\[Cx = AyBz - AzBy Cy = AzBx - AxBz Cz = AxBy - AyBx. \label{11.4} \]
Observe que una vez que tenga la primera de estas ecuaciones, las otras dos se pueden obtener permutando cíclicamente los índices, es decir,\(x \) →\(y\)\(z\),\(y \) → y\(z \) →\(x\). Esto es útil como ayuda para la memoria.
Par y Momentum Angular
El torque es la acción de una fuerza\(F\) sobre una masa\(M \) que la induce a girar alrededor de algún punto, llamado origen. Se define
\[τ = r × F, \label{11.5}\]
donde\(r\) está la posición de la masa con respecto al origen, como se ilustra en la figura 11.2.
Observe que el par es cero en varias circunstancias. Si la fuerza apunta directamente hacia o lejos del origen, el producto cruzado es cero, lo que resulta en un par cero, aunque la fuerza no sea cero. Asimismo, si\(r\) = 0, el par es cero. Así, una fuerza que actúa en el origen no produce par. Ambos límites tienen sentido intuitivamente, ya que ninguno induce a la masa a girar en torno al origen.
El momento angular de una masa\(M \) con respecto a un punto O es
\[L = r × p, \label{11.6}\]
donde\(p\) está el momento cinético ordinario de la masa. 1 El momento angular es cero si el movimiento del objeto es directamente hacia o lejos del origen, o si se encuentra en el origen.
Si tomamos el producto cruzado del vector de posición y la segunda ley de Newton, obtenemos una ecuación que relaciona el par y el momento angular:
\[ dp d dr r × F = r × --- = --(r × p ) ----× p. dt dt dt \label{11.7} \]
El segundo término en el lado derecho de la ecuación anterior es cero porque es\(d\)\(r\)\(∕dt\) igual a la velocidad de la masa, que es paralela a su momento y el producto cruzado de dos vectores paralelos es cero. Por lo tanto, esta ecuación puede escribirse
\[ dL τ = -dt (Newton ’s second law for rotation ). \label{11.8}\]
Es la versión rotacional de la segunda ley de Newton.
Tanto para el par como para el momento angular la ubicación del origen es arbitraria, y generalmente se elige para la máxima comodidad. Sin embargo, es necesario elegir el mismo origen tanto para el par como para el momento angular.

Para el caso de una fuerza central, es decir, una que actúa a lo largo de la línea de centros entre dos objetos (como la gravedad), a menudo existe una elección de origen particularmente conveniente. Imagínese un planeta girando alrededor del sol, como se ilustra en la figura 11.3. Si el origen se coloca en el centro del sol (que se supone que no se mueve bajo la influencia de la gravedad del planeta), entonces el par ejercido sobre el planeta por la gravedad del sol es cero, lo que significa que el momento angular del planeta alrededor del centro del sol es constante en el tiempo. Ninguna otra elección de origen daría este resultado conveniente.
Ya conocemos dos leyes fundamentales de conservación: las de la energía y el impulso lineal. Creemos que el momento angular se conserva de manera similar en sistemas aislados. En otras palabras, las partículas pueden intercambiar momento angular entre ellas, pero la suma vectorial del momento angular de todas las partículas en un sistema aislado de influencias externas debe permanecer constante.
La conservación del momento angular no es una consecuencia automática de la conservación del momento lineal, aunque la ecuación gobernante 11.8} para el momento angular se deriva de la segunda ley de Newton. A modo de ejemplo, la figura 11.4 muestra una situación hipotética en la que la fuerza\(F\) 21 de\(M\) 1 sobre\(M\) 2 es igual en magnitud pero opuesta en signo a la fuerza\(F\) 12 de \(M\)2 sobre\(M\) 1, es decir, sostiene la tercera ley de Newton, y se conserva la suma de los momentos de las dos masas. Sin embargo, debido a que las fuerzas no son centrales, el momento angular de las masas no se conserva. Este escenario es imposible si las fuerzas son centrales.
Partículas
Supongamos que deseamos aplicar la segunda ley de Newton a dos partículas consideradas juntas como un solo sistema. Como mostramos anteriormente, solo las fuerzas externas actúan sobre el impulso total,\(p\) total =\(p\) 1 +\(p\) 2, de las dos partículas:
\[F = dptotal. external dt \label{11.9}\]
Escribamos el impulso no relativista total de las dos partículas de una manera especial:
\[ ( M1v1 + M2v2 ) ptotal = M1v1 + M2v2 = Mtotal ----M--------- ≡ MtotalVcm, total \label{11.10} \]
donde\(M\) total =\(M\) 1 +\(M\) 2. La cantidad\(V\) cm es la velocidad del centro de masa y se puede expresar como la derivada temporal de la posición del centro de masa,\(R\) cm,
\[ dRcm Vcm = -----, dt \label{11.11} \]
donde
\[ M1r1 + M2r2 Rcm = -------------. Mtotal \label{11.12} \]
Ahora vemos cómo la energía cinética y el momento angular de las dos partículas pueden dividirse en dos partes, una teniendo que ver con el movimiento del centro de masa de las dos partículas, la otra teniendo que ver con el movimiento de las dos partículas relativo a su centro de masa. La Figura 11.5 muestra gráficamente cómo los vectores\(r\) ′ 1 =\(r\) 1 -\(R\) cm y\(r\) ′ 2 =\(r\) 2 -\(R\) cm están definidos. Estos vectores representan las posiciones de las dos partículas con respecto al centro de masa. La sustitución en la ecuación 11.12} muestra que\(M\) 1\(r\) ′ 1 +\(M\) 2\(r\) ′ 2 = 0. Esto lleva a la conclusión de que\(M\) 1\(d\) 1 =\(M\) 2\(d\) 2 en la figura 11.5. También definimos la velocidad de cada masa relativa al centro de masa como\(v\) ′ 1 =\(d\)\(r\) ′ 1\(∕dt \) y\(v\) ′ 2 =\(d\) \(r\)′ 2\(∕dt\), y por lo tanto tenemos\(M\) 1\(v\) ′ 1 +\(M\) 2\(v\) ′ 2 = 0.
La energía cinética total es solo la suma de las energías cinéticas de las dos partículas,\(K \) =\(M\) 1\(v\) 1 2\(∕\) 2 +\(M\) 2\(v\) 2 2\(∕\) 2, donde\(v\) 1 y\(v\) 2 son las magnitudes de los vectores de velocidad correspondientes. Sustitución de\(v\) 1 =\(V\) cm +\(v\) ′ 1 etc., en la fórmula de energía cinética y reorganización de rendimientos
\[ 2 ′2 ′2 Ktotal = Ktrans + Kintern = [MtotalVcm∕2 ] + [M1v 1 ∕2 + M2v 2 ∕2]. \label{11.13}\]
Términos como\(V\) cm ⋅\(v\) ′ 1 cancelan porque\(M\) 1\(v\) ′ 1 +\(M\) 2\(v\) ′ 2 = 0.
El primer término en el lado derecho de la ecuación 11.13} entre corchetes es la energía cinética que tendrían las dos partículas si toda la masa se concentrara en el centro de masa. El segundo término es la energía cinética calculada en relación con el movimiento del centro de masa. El primero se llama la energía cinética traslacional del sistema mientras que el segundo se llama la energía cinética interna.
El momento angular del sistema es solo la suma de los momentos angulares de las dos partículas:\(L\) total =\(M\) 1\(r\) 1 ×\(v\) 1 +\(M\) 2\(r\) 2 ×\(v\) 2. Razonando similar al caso de la energía cinética, podemos reescribir esto como
\[L = L + L = [M R × V ] + [M r′× v′+ M r′× v ′]. total orb spin total cm cm 1 1 1 2 2 2 \label{11.14}\]
El primer término entre corchetes a la derecha se denomina momento angular orbital mientras que el segundo término se denomina momento angular de giro. El primero es el momento angular que tendría el sistema si toda la masa se concentrara en el centro de masa, mientras que el segundo es el momento angular de movimiento alrededor del centro de masa.
Curiosamente, la idea del centro de masa y la correspondiente división de la energía cinética y el momento angular en partes orbitales y de espín no tiene una generalización relativista útil. Esto se debe al factor de\(γ \) ≡ (1 -\(v\) 2\(∕c\) 2) - 1 2 en la definición relativista de impulso,\(p\) =\(m\) \(v\)\(γ\), lo que significa que
\[dmr -----⁄= p (relativistic case). dt \label{11.15} \]
Mancuerna desigual
Hasta el momento no hemos puesto restricciones a los movimientos de las dos partículas. Un caso especial interesante ocurre cuando las partículas están conectadas por una varilla ligera y rígida, dándonos una mancuerna. Para simplificar aún más las cosas, suponemos que la varilla está conectada rígidamente a un eje fijo en el centro de masa de las dos partículas, como se muestra en la figura 11.6. Por lo tanto, las masas que constituyen los extremos de la mancuerna son libres de girar en círculos alrededor del eje, pero se les impide ejecutar cualquier otro movimiento. El efecto clave de esta restricción es que ambas masas giran alrededor del eje con la misma frecuencia angular\(ω\).
Si las partículas están respectivamente a distancias\(d\) 1 y\(d\) 2 del eje, entonces sus velocidades son\(v\) 1 =\(d\) 1\(ω \) y\(v\) 2 =\(d\) 2\(ω\). Así, la energía cinética de la mancuerna giratoria es
\[Kintern = 1M1v2 + 1-M2v2 = 1Iω2 (fixed axle), 2 1 2 2 2 \label{11.16}\]
donde\(I \) =\(M\) 1\(d\) 1 2 +\(M\) 2\(d\) 2 2 se llama el momento de inercia. Del mismo modo, la magnitud del momento angular de giro, que es un vector paralelo al eje, es
\[Lspin = M1d1v1 + M2d2v2 = Iω (fixed axle). \label{11.17}\]
Finalmente, la segunda ley de Newton para la rotación se convierte en
\[τ = dLspin = dIω- = I dω- (fixed axle), dt dt dt \label{11.18}\]
donde\(τ \) es el componente del par a lo largo del eje de rotación.
Tenga en cuenta que la expresión más a la derecha en la ecuación 11.18} asume que\(I \) es constante, lo cual solo es cierto si\(d\) 1 y\(d\) 2 son constantes — es decir, la mancuerna debe ser verdaderamente rígida.
Partículas
La generalización de dos partículas a muchas partículas es bastante fácil en principio. Si un subíndice\(i \) indica el valor de una cantidad para la i ésima partícula, entonces el centro de masa viene dado por
\[ --1---∑ Rcm = M Miri total i \label{11.19} \]
donde
\[M = ∑ M . total i i \label{11.20}\]
Además, si definimos\(r\) ′ i =\(r\) i -\(R\) cm, etc., entonces la energía cinética es justa
\[K = M V 2 ∕2 + ∑ M v′2∕2 total total cm i i i \label{11.21}\]
y el momento angular es
\[ ∑ ′ ′ Ltotal = MtotalRcm × Vcm + Mir i × vi. i \label{11.22} \]
En otras palabras, tanto la energía cinética como el momento angular se pueden separar en dos partes: una parte está relacionada con el movimiento general del sistema y la otra se debe a movimientos de los componentes del sistema en relación con el centro de masa, al igual que en el caso de la mancuerna.
Cuerpos Rígidos
Para un cuerpo rígido que gira alrededor de un eje fijo, el momento de inercia es
\[ ∑ I = Mid2i, i \label{11.23} \]
donde\(d\) i es la distancia perpendicular de la i-ésima partícula desde el eje. Las ecuaciones (11.16) - (11.18) son válidas para un cuerpo rígido que consta de muchas partículas. Además, el momento de inercia es constante en este caso, por lo que se puede sacar de la derivada del tiempo:
\[ dIω d ω τ = ---- = I--- = I α (fixed axle, constant I). dt dt \label{11.24} \]
La cantidad\(α \) =\(dω∕dt \) se llama aceleración angular.
La suma en la ecuación para el momento de inercia se puede convertir en una integral para una distribución continua de masa. No vamos a perseguir esto aquí, sino simplemente citar los resultados para una serie de objetos sólidos de densidad uniforme:
- Para la rotación de una esfera de masa\(M \) y radio\(R \) alrededor de un eje perforando su centro:\(I \) = 2\(MR\) 2\(∕\) 5.
- Para rotación de un cilindro de masa\(M \) y radio\(R \) alrededor de su eje de simetría:\(I \) =\(MR\) 2\(∕\) 2.
- Para la rotación de una varilla delgada de masa\(M \) y longitud\(L \) alrededor de un eje perpendicular a la varilla que pasa por su centro:\(I \) =\(ML\) 2\(∕\) 12.
- Para la rotación de un anillo de masa\(M\), radio\(R\) interior a y radio exterior\(R\) b alrededor de su eje de simetría:\(I \) =\(M\) (\(R\)a 2 +\(R\) b 2)\(∕\) 2.
Estática
Si un cuerpo rígido está inicialmente en reposo, permanecerá en reposo si y sólo si la suma de todas las fuerzas y la suma de todos los pares que actúan sobre el cuerpo son cero. Como ejemplo, en la figura 11.7 se muestra un balance de masas con brazos de diferente longitud. La barra de equilibrio está sujeta a tres fuerzas que apuntan hacia arriba o hacia abajo, la tensión\(T \) en la cuerda de la que se suspende la viga y los pesos\(M\) 1\(g \) y\(M\) 2\(g\) ejercidos sobre la viga por los dos suspendidos masas. El parámetro\(g \) es el campo gravitacional local y se supone que el haz de equilibrio en sí tiene una masa insignificante. Tomando hacia arriba como positivo, la condición de fuerza para el equilibrio estático es
\[T - M g - M g = 0 (zero net force). 1 2 \label{11.25}\]
Al definir un par en sentido contrario a las agujas del reloj para que sea positivo, el equilibrio de par calculado alrededor del punto de pivote en la figura 11.
\[τ = M gd - M gd = 0 (zero torque), 1 1 2 2 \label{11.26}\]
donde\(d\) 1 y\(d\) 2 son las longitudes de los brazos de la viga.
La primera de las ecuaciones anteriores muestra que la tensión en la cuerda debe ser
\[T = (M1 + M2 )g, \label{11.27}\]
mientras que el segundo demuestra que
\[M d ---1= -2. M2 d1 \label{11.28} \]
Así, la tensión en la cuerda es igual al peso de las masas unidas a la barra de equilibrio, mientras que la relación de las dos masas es igual a la relación inversa de las longitudes de brazo de viga asociadas.
Problemas
- Mostrar usando la forma componente del producto cruzado dado por la ecuación 11.4} que\(A\) ×\(B\) = -\(B\) ×\(A\).
- }
- Una masa\(M \) se desliza sobre una mesa sin fricción, pero está unida a una cuerda que pasa a través de un orificio en el centro de la mesa como se muestra en la figura 11.8. La cuerda se dibuja gradualmente para que la masa trazar un patrón en espiral como se muestra en la figura 11.8. La distancia inicial de la masa desde el agujero en la tabla es\(R \) y su velocidad tangencial inicial es\(v\). Después de que se dibuja la cuerda, la masa está a una distancia\(R\) ′ del agujero y su velocidad tangencial es\(v\) ′.
- Dado\(R\),\(v\), y\(R\) ′, encontrar\(v\) ′.
- Calcular el cambio en la energía cinética de la masa al ir de radio\(R \) a radio\(R\) ′.
- Si el cambio anterior es distinto de cero, determine de dónde vino la energía extra.
Figura 11.8: Trayectoria de una masa sobre una mesa sin fricción unida a una cuerda que pasa por un agujero en la mesa. La cadena está dibujando la masa en.
_____________________________________
- Un automóvil de masa 1000 kg se dirige hacia el norte por una carretera a 30 m s - 1 que pasa 2 km al este del centro de la ciudad.
- Calcule el momento angular del automóvil sobre el centro de la ciudad cuando el automóvil esté directamente al este de la ciudad.
- Calcule el momento angular del automóvil sobre el centro de la ciudad cuando esté a 3 km al norte del punto anterior.
- El aparato ilustrado en la figura 11.9 se utiliza para levantar un cubo de masa\(M\) fuera de un pozo.
- ¿Qué fuerza se\(F \) debe ejercer para evitar que el cubo vuelva a caer al pozo?
- Si el cubo se eleva lentamente una distancia\(d\), ¿qué trabajo se realiza en el cubo por la cuerda unida a él?
- ¿Qué trabajo se realiza por la fuerza\(F \) en el mango en el caso anterior?
Figura 11.9: Una manivela sobre un eje fijo gira un tambor, enrollando así la cuerda alrededor del tambor y elevando la masa.
_____________________________________
- Derivar ecuaciones (11.13) y (11.14).
- Una masa\(M \) es sostenida por la estructura que se muestra en la figura 11.10. La viga de soporte tiene una masa insignificante. Encuentra la tensión\(T \) en el cable diagonal. Consejo: Calcule el par neto en la viga de soporte alrededor del punto A debido a la tensión\(T \) y al peso de la masa\(M\).
Figura 11.10: Una masa es soportada por la tensión en el cable diagonal. La viga de soporte es libre de pivotar en el punto A.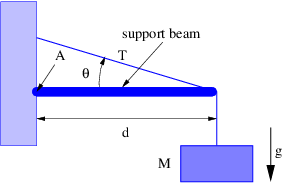
_____________________________________
- Un sistema consta de dos estrellas, una de masa\(M \) moviéndose con velocidad\(v\) 1 = (0\(,v, \) 0) en la posición\(r\) 1 = (\(d, \)\(, \)0 0), la otra de masa 2\(M \) con velocidad cero en el origen.
- Encuentra el centro de la posición de masa y la velocidad del sistema de dos estrellas.
- Encuentra el momento angular de giro del sistema.
- Encuentra la energía cinética interna del sistema.
Figura 11.11: Una masa es soportada por dos cadenas.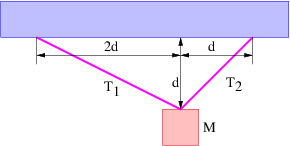
_____________________________________
Figura 11.12: Una escalera apoyada contra una pared se mantiene en su lugar la fuerza\(F \) que actúa sobre la base de la escalera.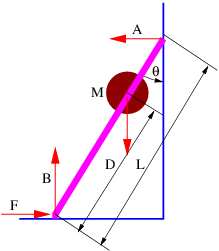
_____________________________________
- Un disco sólido está rodando por una rampa inclinada un ángulo\(θ \) desde la horizontal. Calcular la aceleración del disco por la rampa y compararla con la aceleración de un bloque que se desliza por la rampa sin fricción.
- Una masa\(M \) está suspendida del techo por dos cuerdas como se muestra en la figura 11.11. Encuentra las tensiones en las cuerdas.
- Un hombre de masa\(M \) es una distancia que\(D \) sube por una escalera de longitud\(L \) que forma un ángulo\(θ \) con respecto a la pared vertical como se muestra en la figura 11.12. Tomar la masa de la escalera para que sea insignificante. Encuentre la fuerza\(F \) necesaria para evitar que la escalera se deslice si la pared y el piso no tienen fricción y por lo tanto solo pueden ejercer fuerzas normales\(A \) y\(B \) sobre la escalera.
Capítulo 12 Oscilador armónico
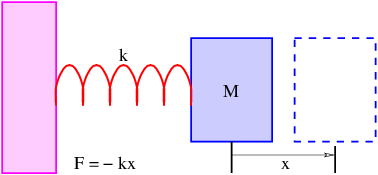
La Figura 12.1 ilustra el oscilador armónico prototípico, el sistema masa-resorte. Una masa\(M \) está unida a un extremo de un resorte. El otro extremo del muelle está unido a algo rígido como una pared. El resorte ejerce una fuerza restauradora\(F \) = -\(kx \) sobre la masa cuando se estira en una cantidad\(x\), es decir, actúa para devolver la masa a su posición inicial. Esto se llama ley de Hooke y\(k \) se llama la constante de primavera.
Análisis Energético
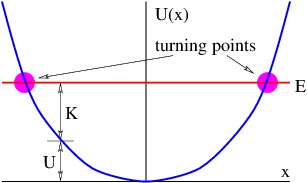
La energía potencial del sistema masa-resorte es
\[ 2 U (x) = kx ∕2 \label{12.1}\]
que podrá verificarse señalando que la fuerza jurídica del Hooke se deriva de esta energía potencial:\(F \) = -\(d\) (\(kx\)2\(∕\) 2)\(∕dx \) = -\(kx\). Esto se muestra en la figura 12.2. Dado que existe una energía potencial, la energía total\(E \) =\(K \) +\(U \) se conserva, es decir, es constante en el tiempo. Si se conoce la energía total, esto proporciona una herramienta útil para determinar cómo varía la energía cinética con la posición\(x \) de la masa\(M\):\(K\) (\(x\)) =\(E \) -\(U\) (\(x\)). Dado que la energía cinética se expresa (no relativisticamente) en términos de la velocidad\(u \) como\(K \) =\(Mu\) 2\(∕\) 2, la velocidad en cualquier punto de la gráfica de la figura 12.2 es
\[ ( )1 ∕2 2(E---U-)- u = ± M . \label{12.2} \]
Ante todo esto, es bastante evidente cómo se mueve la masa. De la ley de Hooke, la masa siempre está acelerando hacia la posición de equilibrio,\(x \) = 0. Sin embargo, en cualquier punto la velocidad puede ser ya sea a la izquierda o a la derecha. En los puntos donde\(U\) (\(x\)) =\(E\), la energía cinética es cero. Esto ocurre en los puntos de inflexión
\[ (2E )1 ∕2 xTP = ± --- . k \label{12.3} \]
Si la masa se mueve hacia la izquierda, se ralentiza a medida que se acerca al punto de inflexión izquierdo. Se detiene cuando llega a este punto y comienza a moverse hacia la derecha. Acelera hasta que pasa la posición de equilibrio y luego comienza a desacelerar, deteniéndose en el punto de inflexión derecho, acelerando hacia la izquierda, etc. La masa oscila así entre los puntos de inflexión izquierdo y derecho. (Tenga en cuenta que las ecuaciones (12.2) y (12.3) solo son ciertas para el oscilador armónico).
¿Cómo depende el periodo de la oscilación de la energía total del sistema? Observe que a partir de la ecuación 12.2} la velocidad máxima de la masa (i. e., la velocidad a\(x \) = 0) es igual a\(u\) max = (2\(E∕M\)) 1 2. La velocidad promedio debe ser alguna fracción de este valor máximo. Adivina aquí que es la mitad de la velocidad máxima:
\[ ( )1∕2 uaverage ≈ umax-= -E-- (approximate ). 2 2M \label{12.4} \]
Sin embargo, la distancia que\(d \) la masa tiene que recorrer para una oscilación completa es el doble de la distancia entre los puntos de inflexión, o\(d \) = 4 (2\(E∕k\)) 1 2. Por lo tanto, el periodo de oscilación debe ser aproximadamente
\[ d ( 2E )1∕2( 2M )1∕2 ( M )1 ∕2 T = u-------≈ 4 -k- -E-- = 8 k-- (approximate ). average \label{12.5} \]
Análisis usando las leyes de Newton
La aceleración de la masa en cualquier momento viene dada por la segunda ley de Newton:
\[ d2x F kx a = ---2 = ---= - ---. dt M M \label{12.6} \]
Una ecuación de este tipo se conoce como ecuación diferencial ya que implica una derivada de la variable dependiente\(x\). Las ecuaciones de este tipo son generalmente más difíciles de resolver que las ecuaciones algebraicas, ya que no existen técnicas universales para resolver todas las formas de tales ecuaciones. De hecho, es justo decir que las soluciones de la mayoría de las ecuaciones diferenciales se obtuvieron originalmente ¡adivinando!
Ya tenemos la base sobre la que hacer una suposición inteligente para la solución a la ecuación 12.6} ya que sabemos que la masa oscila de un lado a otro con un periodo que es independiente de la amplitud de la oscilación. Una función que podría llenar la factura es la función coseno. Intentemos sustituir\(x \) = cos (\(ωt\)), donde\(ω \) es una constante, en esta ecuación. La segunda derivada de\(x\) con respecto a\(t \) es -\(ω\) 2 cos (\(ωt\)), por lo que realizar esta sustitución da como resultado
\[ 2 -k- - ω cos(ωt ) = - M cos(ωt ). \label{12.7}\]
Observe que la función coseno se cancela, dejándonos con -\(ω\) 2 = -\(k∕M\). La conjetura funciona así si establecemos
\[ ( )1∕2 ω = -k- . M \label{12.8} \]
La constante\(ω \) es la frecuencia de oscilación angular para el oscilador, de la cual inferimos que el período de oscilación es\(T \) = 2\(π\) (\(M∕k\)) 1 2. Esto concuerda con el resultado aproximado anterior de la ecuación 12.5}, excepto que la aproximación tiene un factor numérico de 8 en lugar de 2\(π \) ≈ 6. Por lo tanto, ¡la suposición anterior solo está apagada en aproximadamente un 30%!
Es fácil demostrar que\(x \) =\(B\) cos (\(ωt\)) es también una solución de la ecuación 12.6}, donde\(B \) está cualquier constante y\(ω \) = (\(k∕M\)) 1 2. Esto confirma que la frecuencia de oscilación y el período son independientes de la amplitud. Además, la función seno es igualmente válida como solución:\(x \) =\(A\) sin (\(ωt\)), donde\(A \) hay otra constante. De hecho, la solución más general posible es sólo una combinación de estos dos, es decir,
\[x = A sin(ωt) + B cos(ωt) = C cos(ωt - ϕ ). \label{12.9}\]
Los valores de\(A \) y\(B \) dependen de la posición y velocidad de la masa en el tiempo\(t \) = 0. El lado derecho de la ecuación 12.9} muestra una forma alternativa de escribir la solución general del oscilador armónico que utiliza una función coseno con un factor de fase\(ϕ\).
Oscilador Forzado
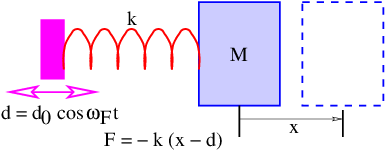
Si movemos el extremo izquierdo del resorte por la cantidad\(d \) =\(d\) 0 cos (\(ω\)F\(t\)), como en la figura 12.3, en lugar de fijarlo rígidamente como en la figura 12.1, tenemos un oscilador armónico forzado. La constante\(d\) 0 es la amplitud del movimiento de meneo impuesto. La frecuencia de forzamiento\(ω\) F no es necesariamente igual a la frecuencia natural o resonante\(ω \) = (\(k∕M\)) 1 2 del sistema masa-resorte. Comportamiento muy diferente ocurre dependiendo de si\(ω\) F es menor que, igual o mayor que\(ω\).
Dado el meneo anterior, la fuerza del resorte sobre la masa se convierte en\(F \) = -\(k\) (\(x \)-\(d\)) = -\(k\) [\(x \)-\(d\) 0 cos (\(ω\)F \(t\))] ya que la longitud del resorte es la diferencia entre las posiciones de los extremos izquierdo y derecho. Procediendo en cuanto al sistema masa-resorte no forzado, llegamos a la ecuación diferencial
\[ 2 d--x + kx-= kd0-cos(ωF t). dt2 M M \label{12.10} \]
La solución a esta ecuación resulta ser la suma de una parte forzada en la que\(x\) es proporcional a cos (\(ω\)F\(t\)) y una parte libre que es la misma que la solución a la ecuación no forzada (12.9). Nos interesa primordialmente la parte forzada de la solución, así que pongamos\(x \) =\(x\) 0 cos (\(ω\)F\(t\)) y sustituyamos esto en la ecuación (12.10):
\[ kx0 kd0 - ω2F x0cos(ωF t) + ----cos(ωF t) = ----cos(ωF t). M M \label{12.11} \]
Nuevamente el factor coseno cancela y nos quedamos con una ecuación algebraica para\(x\) 0, la amplitud del movimiento oscilatorio de la masa.
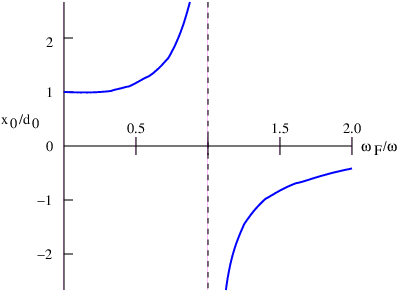
Resolviendo para la relación de la amplitud de oscilación de la masa a la amplitud del movimiento ondulante,\(x\) \(∕d\)0 0, encontramos
\[x0-= -----1-----, d0 1 - ω2F∕ω2 \label{12.12}\]
donde hemos reconocido que\(k∕M \) =\(ω\) 2, el cuadrado de la frecuencia de la oscilación libre. Esta función se representa en la figura 12.4.
Observe que si\(ω\) F\(< ω\), el movimiento de la masa está en fase con el movimiento oscilante y la amplitud de la oscilación de masa es mayor que la amplitud del movimiento. A medida que la frecuencia de forzamiento se acerca a la frecuencia natural del oscilador, la respuesta de la masa crece en amplitud. Cuando el forzamiento está a la frecuencia resonante, la respuesta es técnicamente infinita, aunque en este caso intervendrán límites prácticos sobre la amplitud de la oscilación —por ejemplo, el resorte no puede estirarse ni encogerse una cantidad infinita. En muchos casos la fricción actuará para limitar la respuesta de la masa a forzar cerca de la frecuencia resonante. Cuando la frecuencia de forzamiento es mayor que la frecuencia natural, la masa realmente se mueve en la dirección opuesta al movimiento de meneo, es decir, la respuesta está desfasada con el forzamiento. La amplitud de la respuesta disminuye a medida que la frecuencia de forzamiento aumenta por encima de la frecuencia resonante.
Los osciladores armónicos forzados y libres forman una parte importante de muchos sistemas físicos. Por ejemplo, cualquier cuerpo de material elástico como un puente o un ala de avión tiene modos oscilatorios armónicos. Un problema común de ingeniería es asegurar que dichos modos sean amortiguados por fricción o algún otro mecanismo físico cuando existe la posibilidad de que estos modos salgan por procesos naturales. Una serie de desastres se puede rastrear a una falla en explicar adecuadamente el forzamiento oscilatorio en estructuras de ingeniería.
Soluciones Exponenciales Complejas
Las funciones exponenciales complejas de la forma\(x \) = exp (±\(iωt\)) también constituyen soluciones al oscilador armónico libre gobernado por la ecuación 12.6}. Esto tiene sentido, ya que el exponencial complejo es la suma de senos y cosenos. Sin embargo, para el oscilador armónico sin fricción, las soluciones exponenciales no proporcionan ninguna ventaja particular sobre los senos y los cosenos. Además, los desplazamientos de osciladores son reales, no cantidades complejas.
El principio de superposición resuelve el problema de las soluciones complejas frente a las reales. Para una ecuación como (12.6) que tiene coeficientes reales, si exp (\(iωt\)) es una solución, entonces también lo es exp (-\(iωt\)), por lo que la superposición de estas dos soluciones también es una solución. Además
\[exp(iωt) + exp(- iωt ) = 2cos(ωt) = 2Re [exp (iωt )]. \label{12.13}\]
Esto muestra un atajo para obtener la parte física de una solución exponencial compleja a ecuaciones como la ecuación del oscilador armónico; simplemente tomar la parte real.
Las soluciones exponenciales complejas se hacen propias para ecuaciones más complicadas. Por ejemplo, supongamos que la fuerza sobre la masa en el sistema masa-resorte toma la forma
\[ dx F = - kx - b---. dt \label{12.14} \]
El término que contiene\(b \) representa un efecto de amortiguación por fricción en el oscilador armónico y la ecuación diferencial gobernante se convierte en
\[d2x b dx k ----+ ------+ ---x = 0. dt2 M dt M \label{12.15} \]
Probar la función exponencial exp (\(σt\)) en esta ecuación da como resultado
\[ ⌊ ( 2 )1∕2⌋ σ = 1-⌈- -b-± -b--- 4k- ⌉ = - β ± i(ω2- β2)1∕2 2 M M 2 M 0 \label{12.16} \]
donde hemos establecido
\[ ( )1∕2 -b-- -k- β = 2M ω0 = M . \label{12.17} \]
La cantidad\(ω \) ≡ (\(ω\)0\(β\) 2 - 2 ) 1 2 es la frecuencia real de oscilación del oscilador amortiguado, cuál puede ver es menor que la frecuencia de oscilación\(ω\) 0 que ocurre con la amortiguación apagada. La solución física para el oscilador amortiguado es así
\[x(t) = Re[exp(σt)] = Re [exp (iωt )exp(- βt)] = cos(ωt )exp(- βt) \label{12.18}\]
siempre y cuando\(ω\) 0 2\(> β\) 2. Observe que esta solución está en la forma de una oscilación cos (\(ωt\)) multiplicada por una exp (-\(βt\)) exponencial en descomposición. Esto confirma que el\(b\) término disminuye la amplitud de la oscilación con el tiempo.
Oscilador armónico mecánico cuántico
El oscilador armónico mecánico cuántico comparte la característica de otros problemas de estado ligado mecánico cuántico en que la energía total puede tomar solo valores discretos. El cálculo de estos valores es demasiado difícil para este libro, pero el problema es lo suficientemente importante como para garantizar reportar los resultados aquí. Las energías accesibles a un sistema de masa-resorte mecánico cuántico vienen dadas por la fórmula
\[En = (n + 1∕2)¯h(k ∕M )1∕2, n = 0,1,2,.... \label{12.19}\]
En otras palabras, la diferencia de energía entre los sucesivos niveles de energía mecánica cuántica en este caso es constante e igual a la frecuencia resonante clásica para el oscilador,\(ω \) = (\(k∕M\)) 1 2, veces\(ℏ\).
Problemas
- Un oscilador (no armónico) tiene la función de energía potencial\(U\) (\(x\)) =\(Cx\) 4, donde\(C \) es una constante. ¿Cómo depende la frecuencia de oscilación de la energía? Explica tu razonamiento.
- Demostrar que\(C\) cos (\(ωt \)-\(ϕ\)) es una forma alternativa de escribir\(A\) sin (\(ωt\)) +\(B\) cos (\(ωt\)) al encontrar los valores de\(A \) y\(B \) en términos de las constantes\(C \) y\(ϕ\). Pista: Expandir cos (\(ωt\)-\(ϕ\)) usando la identidad trigonométrica para el coseno de la suma de dos ángulos.
- Si un oscilador armónico masa-resorte tiene desplazamiento\(x \) = 0 y velocidad\(dx∕dt \) =\(V \) en el tiempo\(t \) = 0, determine los valores de\(A \) y así\(B \) como los de\(C \) y\(ϕ \) en la ecuación 12.9}.
- }
- Una masa\(M \) se suspende contra la gravedad por un resorte de constante de resorte\(k\). La longitud no estirada del resorte es\(x\) 0 y bajo la influencia de la gravedad el resorte se estira a una longitud de reposo\(x\) 1\(> x\) 0.
- Calcular la longitud del resorte\(x\) 1 en el caso estable y en reposo.
- Establecer la ecuación de movimiento para la masa que se mueve bajo la influencia de las dos fuerzas, la gravedad y la primavera. Resolver la ecuación para la frecuencia de la oscilación y la posición del resorte en función del tiempo\(x\) (\(t\)). ¿La frecuencia de oscilación cambia de la caja sin gravedad?
- }
- Determinar las dos soluciones reales al problema del oscilador armónico amortiguado en el caso en el que\(ω\) 0 2\(< β\) 2.
Figura 12.5: El péndulo como oscilador armónico.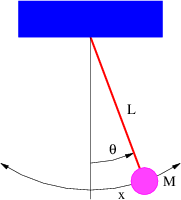
_____________________________________
- Considera el péndulo en la figura 12.5. La masa\(M \) se mueve a lo largo de un arco\(x \) indicando la distancia a lo largo del arco desde el punto de equilibrio.
- Encontrar el componente de la fuerza gravitacional tangente al arco (y así en la dirección del movimiento de la masa) en función del ángulo\(θ\). Usa la aproximación de ángulo pequeño en sin (\(θ\)) para simplificar esta respuesta.
- Obtener la fuerza en términos de\(x \) más que\(θ\). (Recordemos que\(θ \) =\(x∕L\).)
- Utilice la segunda ley de Newton para el movimiento en la\(x \) dirección (es decir, a lo largo del arco seguido de la masa) para obtener la ecuación de movimiento para la masa.
- }
- Resuelve la ecuación de movimiento usando como guía la solución al problema masa-resorte.
- }
- Oscilador amortiguado forzado:
- Agregue un término de amortiguación a la ecuación 12.10} del oscilador armónico forzado y resuelva para la parte forzada de la solución usando métodos exponenciales complejos. Pista: Cambia el coseno del lado derecho de esta ecuación a exp (\(iω\)F\(t\)) para convertir la ecuación a forma compleja y luego prueba la solución\(x \) =\(x\) 0 exp (\(iω\)F\(t\)) donde \(x\)0 dependerá de\(ω\) F. Además, escribe la ecuación en términos de\(β \) =\(b∕\) (2\(M\)) y\(ω\) 2 =\(k∕M\).
- }
- Encuentra la parte física de esta solución tomando la parte real de\(x\) (\(t\)). Pista: Si bien toma la parte real de\(x\), puede ser útil recordar que la inversa de cualquier número complejo se puede escribir 1\(∕\) (\(a \)+\(ib\)) = (\(a \)-\(ib\))\(∕\) (\(a\)2 +\(b\) 2 ).
- Determine en qué se diferencia\(x\) 0 de eso en el caso sin amortiguar cuando\(ω\) F está cerca de la frecuencia resonante del oscilador no forzado. En particular, mostrar cómo la fase y amplitud de la oscilación cambian a medida que la frecuencia de forzamiento cambia de menor a mayor que la frecuencia resonante.
- Una partícula sin masa se limita a una caja de longitud\(a\). (Piense en un fotón entre dos espejos.) Tratando la partícula clásicamente, computar el periodo de un viaje de ida y vuelta de un extremo de la caja al otro y de regreso. A partir de esto se calcula una frecuencia angular para la oscilación de esta partícula en la caja. ¿Esta frecuencia depende de la energía de la partícula?
- Calcular la tierra de energía\(E\) del estado fundamental de una partícula sin masa en una caja de longitud\(a \) usando mecánica cuántica. Comparar el\(E\) suelo\(∕\)\(ℏ\) con la frecuencia angular calculada en el problema anterior.


