1.2: Ondas sinusoidales

Figura\(\PageIndex{1}\): .2: Croquis de definición para una onda sinusoidal, mostrando la longitud de onda\(\lambda\) y la amplitud\(h_{0}\) y la fase\(\phi\) en diversos puntos.

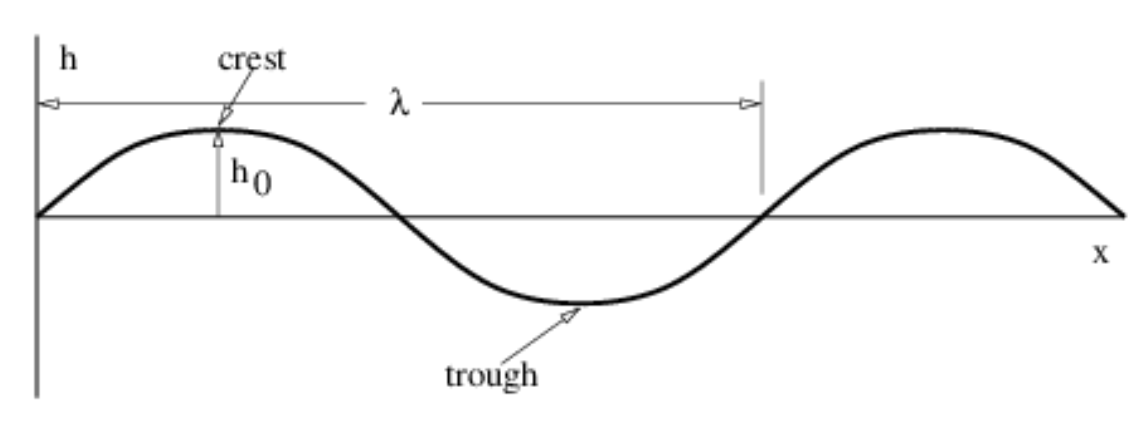
Un tipo de onda particularmente simple, la onda sinusoidal, se ilustra en la figura 1.2. Esto tiene la forma matemática

\[h(x)=h_{0} \sin (2 \pi x / \lambda)\label{1.1}\]

donde h es el desplazamiento (que puede ser longitudinal o transversal), h ₀ es el desplazamiento máximo, también llamado amplitud de la onda, y λ es la longitud de onda. Se supone que el comportamiento oscilatorio de la onda continúa hasta el infinito tanto en la dirección x positiva como en la negativa. Observe que la longitud de onda es la distancia a través de la cual la función sinusoidal completa un ciclo completo. La cresta y el valle de una ola son las ubicaciones de los desplazamientos máximo y mínimo, como se ve en la figura 1.2.

Hasta el momento sólo hemos considerado una onda sinusoidal tal como aparece en un momento determinado. Todas las olas interesantes se mueven con el tiempo. El movimiento de una onda sinusoidal hacia la derecha una distancia d puede explicarse reemplazando x en la fórmula anterior por\(x - d\). Si este movimiento ocurre en el tiempo\(t\), entonces la onda se mueve a velocidad\(c = d∕t\). Resolver esto para d y sustituir produce una fórmula para el desplazamiento de una onda sinusoidal en función tanto de la distancia\(x\) como del tiempo\(t\):

\[h(x, t)=h_{0} \sin [2 \pi(x-c t) / \lambda\label{1.2}\]

El tiempo para que una onda se mueva una longitud de onda se llama el período de la onda:\(T=\lambda / c\). Así, también podemos escribir

\[h(x, t)=h_{0} \sin [2 \pi(x / \lambda-t / T)]\label{1.3}\]

A los físicos realmente les gusta escribir la ecuación para una onda sinusoidal en una forma un poco más simple. Definiendo el número de onda como\(k=2 \pi \lambda\) y la frecuencia angular como\(\omega=2 \pi T\), escribimos

\[h(x, t)=h_{0} \sin (k x-\omega t)\label{1.4}\]

Normalmente pensamos en la frecuencia del movimiento oscilatorio como el número de ciclos completados por segundo. A esto se le llama la frecuencia rotacional, y está dada por\(f=1 / T\). Se relaciona con la frecuencia angular por\(\omega=2 \pi f\). La frecuencia rotacional suele ser más fácil de medir que la frecuencia angular, pero la frecuencia angular tiende a ser utilizada con mayor frecuencia en discusiones teóricas. Como se mostró anteriormente, convertir entre los dos no es difícil. La frecuencia rotacional se mide en unidades de hercios, abreviado Hz;\(1 \mathrm{~Hz}=1 \text { cycle } \mathrm{s}^{-1}\). La frecuencia angular también tiene las dimensiones de tiempo inverso, por ejemplo, radianes s ^-1, pero el término “hercios” generalmente se reserva solo para frecuencia rotacional.

El argumento de la función sinusoidal es por definición un ángulo. Nos referimos a este ángulo como la fase de la onda,\(\phi=k x-\omega t\). La diferencia en la fase de una onda en tiempo fijo sobre una distancia de una longitud de onda es\(2 \pi\), al igual que la diferencia de fase en posición fija durante un intervalo de tiempo de un período de onda.

Dado que los ángulos son adimensionales, normalmente no incluimos esto en las unidades para frecuencia. Sin embargo, a veces aclara las cosas para referirse a las dimensiones de la frecuencia rotacional como “rotaciones por segundo” o frecuencia angular como “radianes por segundo”.

Como se señaló anteriormente, llamamos\(h_{0}\), el desplazamiento máximo de la onda, la amplitud. Muchas veces nos interesa la intensidad de una onda, que es proporcional al cuadrado de la amplitud. La intensidad suele estar relacionada con la cantidad de energía que transporta una ola.

La velocidad de ola que hemos definido anteriormente,\(c=\lambda/T\), en realidad se llama la velocidad de fase. Ya que\(\lambda=2 \pi k \text { and } T=2 \pi / \omega\), podemos escribir la velocidad de fase en términos de la frecuencia angular y el número de onda:

\[c=\frac{\omega}{k} \quad(\text { phase speed })\label{1.5}\]