2.3: Superposición de Ondas Planas

Ahora estudiamos paquetes de ondas en dos dimensiones preguntándonos cómo es la superposición de dos ondas sinusoidales planas. Si las dos ondas tienen números de onda diferentes, pero sus vectores de onda apuntan en la misma dirección, los resultados son idénticos a los presentados en el capítulo anterior, excepto que los paquetes de ondas se alargan indefinidamente sin cambio de forma en la dirección perpendicular al vector de onda. Los paquetes de ondas producidos en este caso se mueven en la dirección de los vectores de onda y así aparecen a un observador estacionario como una serie de pulsos pasantes con amplia extensión lateral.

La superposición de dos ondas planas que tienen la misma frecuencia da como resultado un paquete de ondas estacionarias a través del cual pasan los frentes de onda individuales. Este paquete de ondas también se alarga indefinidamente en alguna dirección, pero la dirección del alargamiento depende de la relación de dispersión para las ondas que se están considerando. Estos paquetes de ondas están en forma de haces constantes, que guían las ondas de fase individuales en alguna dirección, pero no cambian por sí mismas con el tiempo. Al superponer múltiples ondas planas, todas con la misma frecuencia, en realidad se puede producir un solo haz estacionario, así como se puede producir un pulso aislado superponiendo múltiples ondas con vectores de onda apuntando en la misma dirección.

Si la frecuencia de una onda depende de la magnitud del vector de onda, pero no de su dirección, la relación de dispersión de la onda se denomina isotrópica; de lo contrario, es anisotrópica. En el caso isotrópico, dos ondas tienen la misma frecuencia solo si las longitudes de sus vectores de onda, y por lo tanto sus longitudes de onda, son las mismas. Los dos primeros ejemplos de la figura 2.6 satisfacen esta condición, mientras que el último es anisotrópico.

Figura\(\PageIndex{2}\): .7: Frentes de onda y vectores de onda (k ₁ y k ₂) de dos ondas planas con la misma longitud de onda pero orientadas en diferentes direcciones. Las bandas verticales muestran regiones de interferencia constructiva donde coinciden los frentes de onda. Las regiones verticales en el medio tienen interferencia destructiva y, por lo tanto, definen los límites laterales de los haces producidos por la superposición. También se muestran las cantidades k ₀ y Δ k.

Figura\(\PageIndex{2}\): .8: Ejemplo de haces producidos por dos ondas planas con la misma longitud de onda que se mueven en diferentes direcciones. Los vectores de onda de las dos ondas son k = (±0.1, 1.0). Las regiones de desplazamiento positivo son más claras, mientras que las regiones de desplazamiento negativo son más oscuras.

Ahora utilizamos el lenguaje de vectores para investigar la superposición de dos ondas planas con los vectores de onda k ₁ y k ₂:

\[h=\sin \left(\mathbf{k}_{1} \cdot \mathbf{x}-\omega t\right)+\sin \left(\mathbf{k}_{2} \cdot \mathbf{x}-\omega t\right)\label{2.15}\]

Aplicando la identidad trigonométrica para el seno de la suma de dos ángulos (como hemos hecho anteriormente), la ecuación (\ ref {2.15}) puede reducirse a

\[h=2 \sin \left(\mathbf{k}_{0} \cdot \mathbf{x}-\omega t\right) \cos (\Delta \mathbf{k} \cdot x)\label{2.16}\]

donde

\[\mathbf{k}_{0}=\left(\mathbf{k}_{1}+\mathbf{k}_{2}\right) / 2 \quad \Delta \mathbf{k}=\left(\mathbf{k}_{2}-\mathbf{k}_{1}\right) / 2\label{2.17}\]

Esto es en forma de onda sinusoidal que se mueve en la dirección k ₀ con velocidad de fase\(c_{\text {phase }}=\omega / |\mathbf{k}_{0}|\) y número de onda\(\left|\mathbf{k}_{0}\right|\), modulada en la dirección Δ k por una función coseno. Las líneas de interferencia destructiva son normales a Δ k. La distancia w entre líneas de interferencia destructiva es la distancia entre ceros sucesivos de la función coseno en la ecuación (\ ref {2.16}), lo que implica que\(|\Delta \mathbf{k}| w=\pi\), lo que lleva a

\[w=\pi /|\Delta \mathbf{k}|\label{2.18}\]

Así, cuanto menor mayor es\(|\Delta \mathbf{k}|\) el diámetro de la viga.

Ondas de longitud de onda idéntica

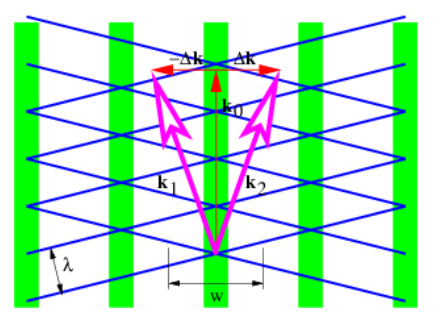
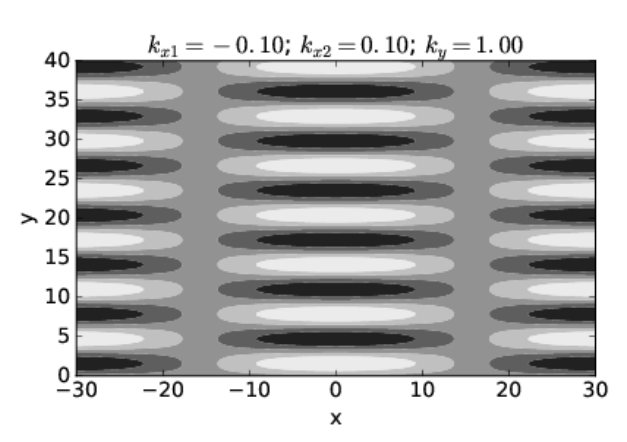
En esta sección investigamos los haces producidos por la superposición de ondas isotrópicas de la misma frecuencia. La Figura 2.7 ilustra lo que sucede en tal superposición. Los vectores k ₁ y k ₂ de igual longitud dan lugar a un vector de onda media k ₀ y la mitad de la diferencia, Δ k. Como se ilustra, las líneas de interferencia constructiva y destructiva son perpendiculares a Δ k. La Figura 2.8 muestra un ejemplo concreto de los haces producidos por superposición de dos ondas planas de igual longitud de onda orientadas como en la figura 2.7. Los haces están alineados verticalmente, ya que Δ k es horizontal, con las líneas de interferencia destructiva que separan los haces ubicados cerca de x = ±16. El ancho transversal de las vigas de ≈ 32 satisface la ecuación (\ ref {2.18}) con |Δ k | = 0.1. Cada haz está formado por ondas de fase que se propagan verticalmente, con las crestas y valles indicados por las regiones de blanco y negro.

Ondas de diferente longitud de onda

En el tercer ejemplo de la figura 2.6, la frecuencia de la onda depende únicamente de la dirección del vector de onda, independientemente de su magnitud, que es lo contrario del caso para una relación de dispersión isotrópica. En este caso altamente anisotrópico, diferentes ondas planas con la misma frecuencia tienen vectores de onda que apuntan en la misma dirección, pero tienen diferentes longitudes.

Figura\(\PageIndex{2}\): .9: Frentes de onda y vectores de onda (k ₁ y k ₂) de dos ondas planas con diferentes longitudes de onda orientadas en diferentes direcciones. Las bandas inclinadas muestran regiones de interferencia constructiva donde coinciden los frentes de onda. Las regiones inclinadas entre ellas tienen interferencia destructiva, y como se mencionó anteriormente, definen los límites laterales de las vigas producidas por la superposición. También se muestran las cantidades k ₀ y Δ k.

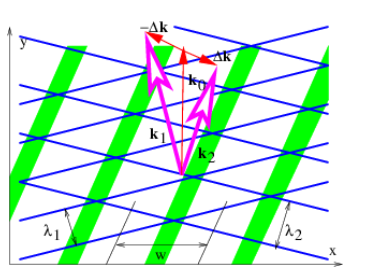
De manera más general, uno podría tener ondas para las cuales la frecuencia depende tanto de la dirección como de la magnitud del vector de onda. En este caso, dos ondas planas diferentes con la misma frecuencia normalmente tendrían vectores de onda que difieren tanto en dirección como en magnitud. Tal ejemplo se ilustra en las figuras 2.9 y 2.10.

Figura\(\PageIndex{2}\): .10: Ejemplo de haces producidos por dos ondas planas con vectores de onda que difieren tanto en dirección como en magnitud. Los vectores de onda de las dos ondas son k ₁ = (-0.1, 1.0) y k ₂ = (0.1, 0.9). Las regiones de desplazamiento positivo son más claras, mientras que las regiones de desplazamiento negativo son más oscuras.

Figura\(\PageIndex{2}\): .11: Ilustración de factores que ingresan a la suma de dos ondas planas con la misma frecuencia. Los frentes de onda son perpendiculares al promedio vectorial de los dos vectores de onda\(\mathbf{k}_{0}=\left(\mathbf{k}_{1}+\mathbf{k}_{2}\right) / 2\), mientras que las líneas de interferencia constructiva, que definen la orientación del haz, están orientadas perpendicularmente a la diferencia entre estos dos vectores,\(\Delta \mathbf{k}=\left(\mathbf{k}_{2}-\mathbf{k}_{1}\right) / 2\)

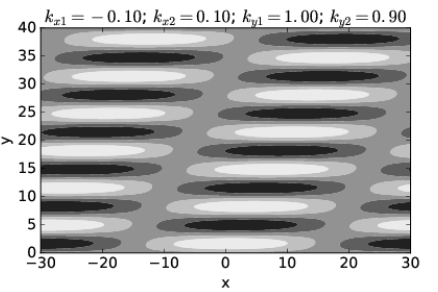
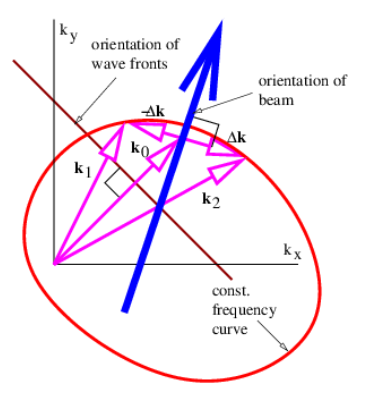
La Figura 2.11 resume lo que hemos aprendido sobre la adición de ondas planas con la misma frecuencia. En general, la orientación del haz (y las líneas de interferencia constructiva) no son perpendiculares a los frentes de onda. Esto solo ocurre cuando la frecuencia de onda es independiente de la dirección del vector de onda.

Ondas con la misma longitud de onda

Al igual que con los paquetes de ondas en una dimensión, podemos sumar más de dos ondas para producir un paquete de ondas aisladas. Aquí limitaremos nuestra atención al caso de una relación de dispersión isotrópica en la que todos los vectores de onda para una frecuencia dada son de la misma longitud.

Figura\(\PageIndex{2}\): .12: Ilustración de vectores de onda de ondas planas que podrían sumarse juntas.

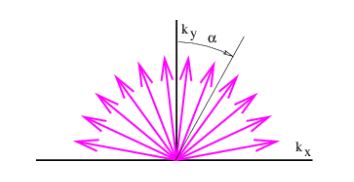
La Figura 2.12 muestra un ejemplo de esto en el que se suman vectores de onda de la misma longitud de onda pero diferentes direcciones. Definiendo\(\alpha_{i}\) como el ángulo del vector de\(i_{th}\) onda en sentido horario desde la vertical, como se ilustra en la figura 2.12, podríamos escribir la superposición de estas ondas en el tiempo t = 0 como

\ [\ begin {ecuación}
\ begin {alineada}
h &=\ suma_ {i} h_ {i}\ sin\ izquierda (k_ {x i} x+k_ {y i} y\ derecha)\\
&=\ suma_ {i} h_ {i}\ sin\ izquierda [k x\ sin\ izquierda (\ alpha_ {i}\ derecha) +k\ y cos\ izquierda (\ alfa_ {i}\ derecha)\ derecha]
\ final {alineado}
\ final {ecuación}\ etiqueta { 2.19}\]

donde lo hemos asumido\(k_{x i}=k \sin \left(\alpha_{i}\right) \text { and } k_{y i}=k \cos \left(\alpha_{i}\right)\). El parámetro\(k=|\mathbf{k}|\) es la magnitud del vector de onda y es el mismo para todas las ondas. Supongamos también en este ejemplo que la amplitud de cada componente de onda disminuye con el aumento\(\left|\alpha_{i}\right|:\).

\[h_{i}=\exp \left[-\left(\alpha_{i} / \alpha_{\max }\right)^{2}\right]\label{2.20}\]

La función exponencial disminuye rápidamente a medida que su argumento se vuelve más negativo, y para fines prácticos, solo los vectores de onda con\(\left|\alpha_{i}\right| \leq \alpha_{m a x}\) contribuyen significativamente a la suma. Nosotros llamamos\(\alpha_{\max }\) el ángulo de propagación.

Figura\(\PageIndex{2}\): .13: Gráfica del campo de desplazamiento h (x, y) a partir de la ecuación (2.19) para α _max = 0.8 y k = 1.

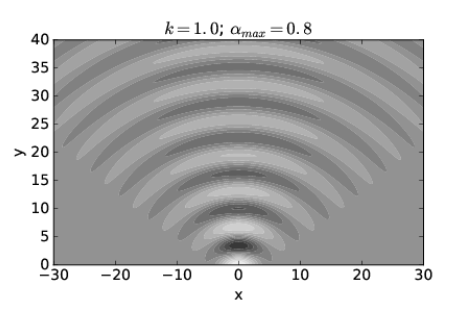
La Figura 2.13 muestra cómo se ve h (x, y) cuando\(\alpha_{\max }=0.8\) radianes y\(k = 1\). Observe que para y = 0 la amplitud de onda solo es grande para una región pequeña en el rango\(-4 < x < 4\). Sin embargo, para\(y > 0\) la onda se extiende en un patrón amplio y semicircular.

Figura\(\PageIndex{2}\): .14: Gráfica del campo de desplazamiento h (x, y) a partir de la ecuación (2.19) para\(\alpha_{\max }=0.2 \text { and } k=1\).

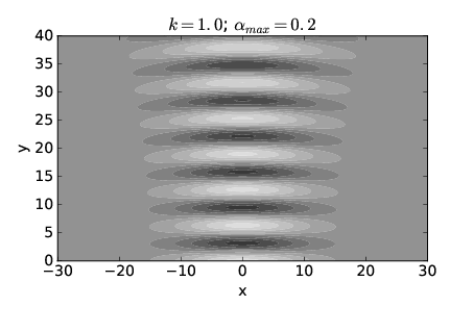
La Figura 2.14 muestra el patrón calculado de h (x, y) cuando el ángulo de dispersión\(\alpha_{\max }=0.2\) radiana. La amplitud de onda es grande para un rango mucho más amplio de\(x\) at\(y = 0\) en este caso, aproximadamente\(-12 < x < 12\). Por otro lado, la propagación posterior de la ola es mucho menor que en el caso de la figura 2.13.

Concluimos que una superposición de ondas planas con vectores de onda extendidos estrechamente alrededor de un vector de onda central que apunta en la dirección y (como en la figura 2.14) produce un haz que inicialmente es ancho en x pero para el cual la anchura aumenta solo ligeramente al aumentar y; sin embargo, una superposición de plano las ondas con vectores de onda diseminados más ampliamente (como en la figura 2.13) producen un haz que inicialmente es estrecho en x pero que aumenta rápidamente en anchura a medida que aumenta y.

La relación entre el ángulo de dispersión\(\alpha_{\max }\) y la amplitud inicial del haz se hace más comprensible en comparación con los resultados de la superposición de dos ondas discutidos al inicio de esta sección. Como lo indica la ecuación (\ ref {2.18}), los valores grandes de\(k_{x}\), y por lo tanto α, están asociados con dimensiones de paquetes de onda pequeña en la dirección x y viceversa. La superposición de dos ondas no captura la propagación posterior del haz que ocurre cuando se superponen muchas ondas, pero sí conduce a una relación cuantitativa aproximada entre α _max (que es solo\(\tan ^{-1}\left(k_{t} / k_{y}\right)\) en el caso de dos ondas) y la anchura inicial del haz. Si invocamos la aproximación de ángulo pequeño para α = α _max para que\(\alpha_{\max }=\tan ^{-1}\left(k_{t} / k_{y}\right) \approx k_{t} / k_{y} \approx k_{t} k,\) entonces k _x ≈ kα _max y la ecuación (\ ref {2.18}) puedan escribirse\(w=\pi k_{x} \approx \pi\left(k \alpha_{\max }\right)=\lambda\left(2 \alpha_{\max }\right)\). Así, podemos encontrar el ángulo de dispersión aproximado a partir de la longitud de onda de la onda λ y la anchura inicial del haz w:

\[\alpha_{\max } \approx \lambda /(2 w) \quad \text { (single slit spreading angle) }\label{2.21}\]