3.4: Ecuación de Lente Delgada e Instrumentos Ópticos

Última actualización
Guardar como PDF

Page ID: 126119

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Dadas las leyes de reflexión y refracción, se puede ver en principio cómo se podía rastrear el paso de la luz a través de un instrumento óptico. Para cada uno de un número de rayos iniciales, se puede calcular el cambio en la dirección del rayo en cada superficie especular o interfaz de índice de refracción. Entre estos puntos, el rayo traza una línea recta.

Figura\(\PageIndex{3}\): .4: Flexión de un rayo de luz a medida que pasa a través de un prisma.

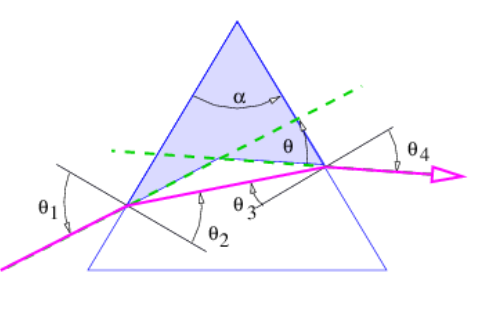
Aunque de concepción simple, este procedimiento puede ser bastante complejo en la práctica. Sin embargo, el procedimiento simplifica si una serie de aproximaciones, llamadas colectivamente aproximación de lente delgada, son válidas. Comenzamos con el cálculo de la flexión de un rayo de luz a medida que pasa por un prisma, como se ilustra en la figura 3.4.

Las piezas de información necesarias para encontrar\(\theta\), el ángulo a través del cual se desvía el rayo, son las siguientes: la geometría del triángulo definida por los puntos de entrada y salida del rayo y el vértice superior del prisma conduce a

\[\alpha+\left(\pi / 2-\theta_{2}\right)+\left(\pi / 2-\theta_{3}\right)=\pi\label{3.5}\]

lo que simplifica

\[\alpha=\theta_{2}+\theta_{3}\label{3.6}\]

La ley de Snell en los puntos de entrada y salida del rayo nos dicen que

\[n=\frac{\sin \left(\theta_{1}\right)}{\sin \left(\theta_{2}\right)} \quad n=\frac{\sin \left(\theta_{4}\right)}{\sin \left(\theta_{3}\right)}\label{3.7}\]

donde n es el índice de refracción del prisma. (Se supone que el índice de refracción del entorno es la unidad.) También se puede inferir que

\[\theta=\theta_{1}+\theta_{4}-\alpha\label{3.8}\]

Esto viene del hecho de que la suma de los ángulos internos del cuadriángulo sombreado en la figura 3.4 es

\[\left(\pi / 2-\theta_{1}\right)+\alpha+\left(\pi / 2-\theta_{4}\right)+(\pi+\theta)=2 \pi .\label{3.9}\]

La combinación de ecuaciones (\ ref {3.6}), (\ ref {3.7}) y (\ ref {3.8}) permite determinar la deflexión del rayo θ en términos de θ ₁ y α, pero la expresión resultante es muy desordenada. Sin embargo, se produce una gran simplificación si se cumplen las siguientes condiciones:

El ángulo α 1.
Los ángulos θ ₁, θ ₂, θ ₃, θ ₄ 1.

Con estas aproximaciones es fácil demostrar que

\[\theta=\alpha(n-1) \quad(\text { small angles })\label{3.10}\]

Figura\(\PageIndex{3}\): .5: Rayos de luz sometidos a deflexión a través de un ángulo\(\theta\) por una lente. El ángulo α es el ángulo entre las tangentes a los puntos de entrada y salida del rayo en la lente.

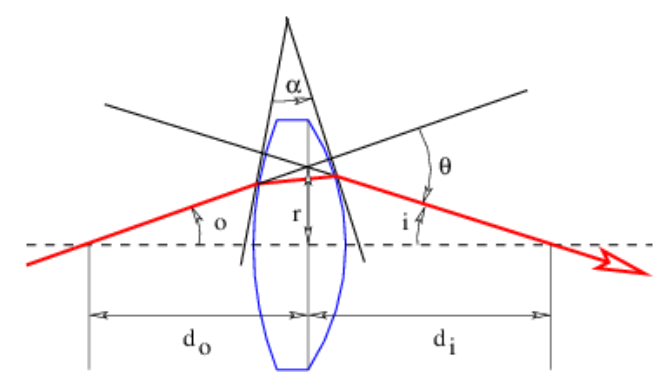
En términos generales, las lentes y espejos en los instrumentos ópticos tienen superficies curvas en lugar de planas. Sin embargo, todavía podemos usar las leyes para la reflexión y refracción por superficies planas siempre que el segmento de la superficie sobre la que incide el paquete de ondas no esté muy curvado en la escala de las dimensiones del paquete de ondas. Esta condición es fácil de satisfacer con la luz que incide en los instrumentos ópticos ordinarios. En este caso, la deflexión de un rayo de luz viene dada por la ecuación (\ ref {3.10}) si α se define como la intersección de las líneas tangentes a los puntos de entrada y salida del rayo, como se ilustra en la figura 3.5.

Una lente positiva es más gruesa en el centro que en los bordes. El ángulo\(\alpha\) entre las líneas tangentes a las dos superficies de la lente a una\(r\) distancia del eje central toma la forma\(\alpha=C r\), donde\(C\) es una constante. El ángulo de deflexión de un haz que golpea la lente a una\(r\) distancia del centro es\(\theta=C r(n-1)\), por lo tanto, como se indica en la figura 3.5. Los ángulos o e i se suman al ángulo de deflexión:\(o+i=\theta=C r(n-1)\). Sin embargo, en la medida en que se sostiene la aproximación de ángulo pequeño,\(o=r / d_{o} \text { and } i=r / d_{i} \text { where } d_{o}\) es la distancia al objeto y\(d_{i}\) es la distancia a la imagen del objeto. Armando estas ecuaciones y cancelando los\(r\) resultados en la ecuación de lente delgada:

\[\frac{1}{d_{o}}+\frac{1}{d_{i}}=C(n-1) \equiv \frac{1}{f}\label{3.11}\]

La cantidad f se denomina distancia focal de la lente. Observe que\(f=d_{i}\) si el objeto está muy lejos de la lente, es decir, si d _o es extremadamente grande.

Figura\(\PageIndex{3}\): .6: Lente positiva que produce una imagen a la derecha de la flecha a la izquierda.

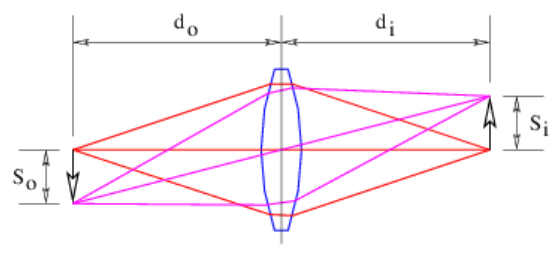
La Figura 3.6 muestra cómo una lente positiva hace una imagen. La imagen es producida por toda la luz de cada punto del objeto que cae sobre un punto correspondiente de la imagen. Si la flecha de la izquierda es un objeto iluminado, aparecerá una imagen de la flecha a la derecha si se permite que la luz que viene de la lente caiga sobre una hoja de papel o una pantalla de vidrio esmerilado. El tamaño del objeto S _o y el tamaño de la imagen S _i están relacionados por geometría simple con las distancias del objeto y la imagen desde la lente:

\[\frac{S_{i}}{S_{o}}=\frac{d_{i}}{d_{o}}\label{3.12}\]

Observe que una lente positiva invierte la imagen.

Figura\(\PageIndex{3}\): .7: Producción de una imagen virtual mediante una lente positiva.

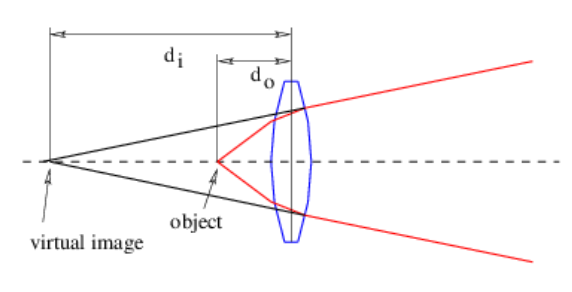
Se producirá una imagen a la derecha de la lente solo si d _o > f. Si d _o < f, la lente es incapaz de converger los rayos de la imagen a un punto, como se ve en la figura 3.7. Sin embargo, en este caso la extensión hacia atrás de los rayos converge en un punto llamado imagen virtual, que en el caso de una lente positiva siempre está más lejos de la lente que del objeto. La imagen se llama virtual porque no aparece en una pantalla de vidrio esmerilado colocada en este punto. A diferencia de la imagen real que se ve en la figura 3.6, la imagen virtual no se invierte. La ecuación de lente delgada todavía se aplica si la distancia desde la lente a la imagen se toma para ser negativa.

Figura\(\PageIndex{3}\): .8: Producción de una imagen virtual mediante una lente negativa.

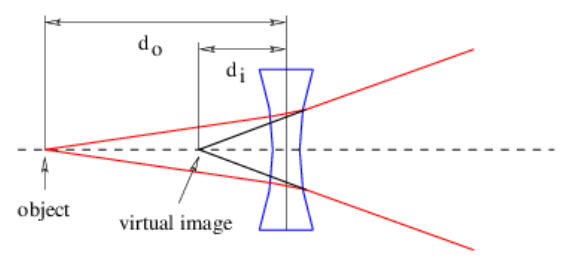
Una lente negativa es más delgada en el centro que en los bordes y produce solo imágenes virtuales. Como se ve en la figura 3.8, la imagen virtual producida por una lente negativa está más cerca de la lente que el objeto. Nuevamente, la ecuación de lente delgada sigue siendo válida, pero tanto la distancia de la imagen a la lente como la distancia focal deben tomarse como negativas. Sólo la distancia al objeto permanece positiva.

Figura\(\PageIndex{3}\): .9: Producción de una imagen real mediante un espejo cóncavo.

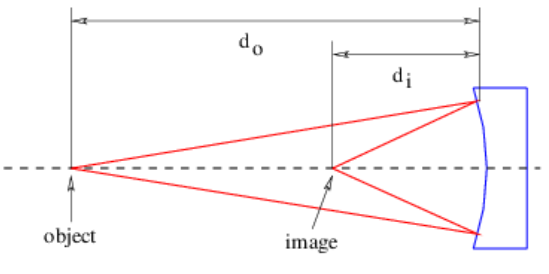
Los espejos curvos también producen imágenes de manera similar a una lente, como se muestra en la figura 3.9. Un espejo cóncavo, como se ve en esta figura, trabaja en analogía con una lente positiva, produciendo una imagen real o virtual dependiendo de si el objeto está más alejado o más cerca del espejo que la distancia focal del espejo. Un espejo convexo actúa como una lente negativa, produciendo siempre una imagen virtual. La ecuación de lente delgada funciona en ambos casos siempre y cuando los ángulos sean pequeños.