3.5: Principio de Fermat

Un enfoque alternativo a la óptica geométrica se puede desarrollar desde el principio de Fermat. Este principio establece (en su forma más simple) que las ondas de luz de una frecuencia dada atraviesan la trayectoria entre dos puntos que toma el menor tiempo. El ejemplo más obvio de ello es el paso de la luz a través de un medio homogéneo en el que la velocidad de la luz no cambia con la posición. En este caso el menor tiempo corresponde a la distancia más corta entre los puntos, que, como todos sabemos, es una línea recta. Así, el principio de Fermat es consistente con la luz que viaja en línea recta en un medio homogéneo.

Figura\(\PageIndex{3}\): .10: Croquis de definición para derivar la ley de reflexión a partir del principio de Fermat. θ _I es el ángulo de incidencia y θ _R el ángulo de reflexión como en la figura 3.1.

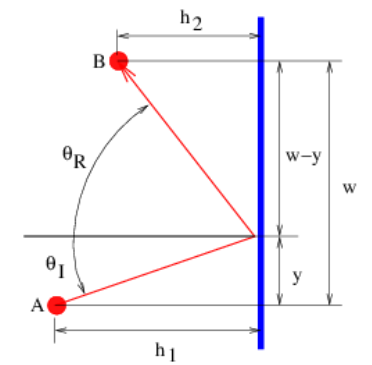
El principio de Fermat también puede ser utilizado para derivar las leyes de reflexión y refracción. Por ejemplo, la figura 3.10 muestra un rayo candidato a reflexión en el que los ángulos de incidencia y reflexión no son iguales. El tiempo requerido para que la luz pase del punto A al punto B es

\[t=\left(\left[h_{1}^{2}+y^{2}\right]^{1 / 2}+\left[h_{2}^{2}+(w-y)^{2}\right]^{1 / 2}\right) / c\label{3.13}\]

donde c es la velocidad de la luz. Encontramos el tiempo mínimo diferenciando t con respecto a y y estableciendo el resultado a cero, con el resultado que

\[\frac{y}{\left[h_{1}^{2}+y^{2}\right]^{1 / 2}}=\frac{w-y}{\left[h_{2}^{2}+(w-y)^{2}\right]^{1 / 2}}\label{3.14}\]

Sin embargo, observamos que el lado izquierdo de esta ecuación es simplemente sin θ _I, mientras que el lado derecho es sin θ _R, de manera que la condición de tiempo mínimo se reduce a sin θ _I = sin θ _R o θ _I = θ _R, que es la ley de reflexión.

Figura\(\PageIndex{3}\): .11: Croquis de definición para derivar la ley de refracción de Snell a partir del principio de Fermat. El área sombreada tiene índice de refracción n > 1.

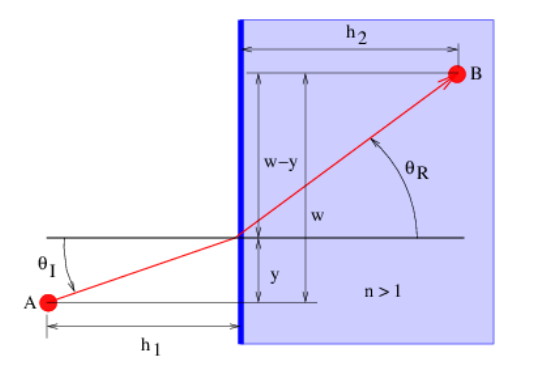
Se puede hacer un análisis similar para derivar la ley de refracción de Snell. La velocidad de la luz en un medio con índice de refracción n es cn, donde c es su velocidad en vacío. Así, el tiempo requerido para que la luz vaya a cierta distancia en tal medio es n veces el tiempo que la luz tarda en recorrer la misma distancia en un vacío. Refiriéndose a la figura 3.11, el tiempo requerido para que la luz pase de A a B se convierte en

\[t=\left(\left[h_{1}^{2}+y^{2}\right]^{1 / 2}+n\left[h_{2}^{2}+(w-y)^{2}\right]^{1 / 2}\right) / c\label{3.15}\]

Esto da como resultado la condición

\[\sin \theta_{I}=n \sin \theta_{R}\label{3.16}\]

donde θ _R es ahora el ángulo refractado. Reconocemos este resultado como la ley de Snell.

Observe que el caso de reflexión ilustra un punto sobre el principio de Fermat: El tiempo mínimo puede ser en realidad un mínimo local más que global — después de todo, en la figura 3.10, ¡la distancia mínima global de A a B sigue siendo solo una línea recta entre los dos puntos! De hecho, la luz a partir del punto A llegará al punto B por ambas rutas —la ruta directa y la ruta reflejada.

Figura\(\PageIndex{3}\): .12: Espejo elipsoidal que muestra rayos de tiempo mínimo y máximo desde el centro del elipsoide hasta la superficie del espejo y hacia atrás nuevamente.

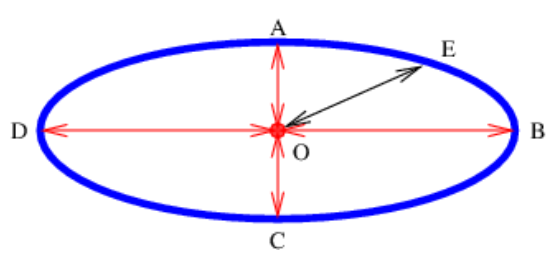
Resulta que las trayectorias permitidas por el principio de Fermat no tienen que ser estrictamente trayectorias de tiempo mínimo. También pueden ser trayectorias de tiempo máximo, como se ilustra en la figura 3.12. En este caso, la luz emitida en el punto O puede reflejarse de vuelta al punto O desde cuatro puntos en el espejo, A, B, C y D. Las trayectorias O-A-O y O-C-O son trayectorias de tiempo mínimo mientras que O-B-O y O-D-O son trayectorias de tiempo máximo.

El principio de Fermat parece bastante misterioso. No obstante, el físico estadounidense Richard Feynman le dio sentido al invocar un principio aún más fundamental, como vemos ahora.

Si un rayo de luz se origina en el punto O de la figura 3.12, se refleja en la superficie elipsoidal del espejo en el punto A, y vuelve al punto O, el tiempo transcurrido no es muy diferente del que experimenta un rayo que se refleja en el espejo a una ligera distancia del punto A y vuelve a O. Esto se debe a que en el punto A haz desde el punto O es perpendicular a la tangente a la superficie del espejo en el punto A. En contraste, el tiempo experimentado por un rayo que va desde el punto O al punto E y hacia atrás diferiría en una cantidad mucho mayor que el tiempo experimentado por un rayo reflejando en el espejo una ligera distancia del punto E. porque la tangente a la superficie del espejo en el punto E no es perpendicular a la viga desde el punto O.

Técnicamente, el cambio en el tiempo de ida y vuelta varía linealmente con la desviación en el punto de reflexión desde el punto E, pero cuadráticamente con la desviación del punto A. Si esta desviación es pequeña en primer lugar, entonces el cambio en el tiempo de ida y vuelta será mucho menor para el caso cuadrático que para el caso lineal.

Parece extraño que habláramos de un haz reflejando de nuevo al punto O si choca contra el espejo en cualquier punto excepto A, B, C o D, debido a los requisitos de la ley de reflexión. No obstante, recordemos que la propia ley de reflexión depende del principio de Fermat, por lo que no podemos asumir la validez de esa ley en esta investigación.

Feynman postuló que los rayos de luz exploran todos los caminos posibles de un punto a otro, pero que los únicos caminos realizados en la naturaleza son aquellos para los cuales la luz que toma caminos cercanos experimenta casi el mismo tiempo transcurrido (o más generalmente, atraviesa casi el mismo número de longitudes de onda) como el camino original. Si esto es cierto, entonces los rayos vecinos interfieren constructivamente entre sí, resultando en un haz mucho más brillante de lo que ocurriría en ausencia de esta interferencia constructiva. Así, las rutas de ida y vuelta O-A-O, O-B-O, O-C-O y O-D-O en la figura 3.12 ocurren realmente, pero no O-E-O. ¡Feynman explica el principio de Fermat invocando interferencias constructivas y destructivas!

Figura\(\PageIndex{3}\): .13: Trayectorias de rayos desde un punto O siendo enfocadas a otro punto I por una lente.

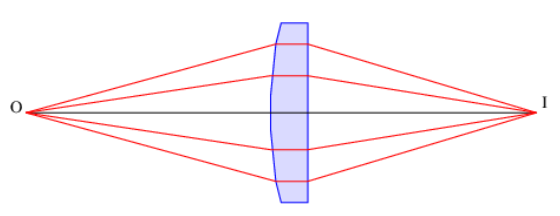
La figura 3.13 ilustra una situación bastante peculiar. Observe que todos los rayos del punto O que interceptan la lente terminan en el punto I. Esto parecería contradecir el principio de Fermat, en que solo deberían ocurrir las trayectorias de tiempo mínimo (o máximo). Sin embargo, un cálculo muestra que todas las trayectorias ilustradas en este caso particular toman el mismo tiempo. Así, la luz no puede elegir una trayectoria sobre otra usando el principio de Fermat y todas las trayectorias son igualmente favorecidas. Tenga en cuenta que esta inferencia se aplica no a cualquier conjunto de trayectorias, sino solo a aquellas que van desde un punto de objeto hasta el punto de imagen correspondiente.