8.6: Movimiento en Dos y Tres Dimensiones

Cuando una onda de materia se mueve a través de una región de energía potencial variable en una dimensión, solo cambia el número de onda. En dos o tres dimensiones, el vector de onda puede cambiar tanto en dirección como en magnitud. Esto complica el cálculo del movimiento de las partículas. No obstante, ya tenemos un ejemplo de cómo manejar esta situación, es decir, la refracción de la luz. En ese caso la ley de Snell nos dice cómo cambia la dirección del vector de onda, mientras que la relación de dispersión combinada con la constancia de la frecuencia nos da información sobre el cambio en la magnitud del vector de onda. Para las ondas de materia funciona un procedimiento similar, aunque los detalles son diferentes, porque buscamos las consecuencias de un cambio en la energía potencial más que un cambio en el índice de refracción.

Figura 8.2: Refracción de una onda de materia por una discontinuidad en la energía potencial. El componente del vector de onda paralelo a la discontinuidad\(\mathrm{k}_{\mathrm{y}}\),, no cambia, entonces\(\mathrm{k}_{1 \mathrm{y}}=\mathrm{k}_{2 \mathrm{y}}\).

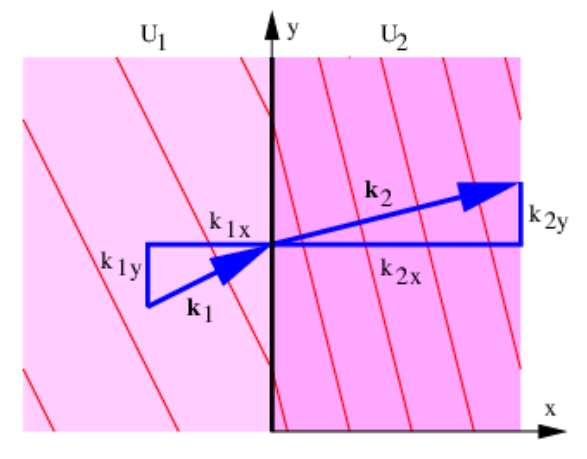
La Figura 8.2 ilustra la refracción de las ondas de materia a una discontinuidad en la energía potencial. Supongamos que la discontinuidad se produce en\(x=0\). Si la onda de materia a la izquierda de la discontinuidad es\(\Psi_{1}=\sin \left(\mathrm{k}_{1 \mathrm{x}} \mathrm{x}+\mathrm{k}_{1 \mathrm{y}} \mathrm{y}-\omega_{1} \mathrm{t}\right)\) y a la derecha es\(\Psi_{2}=\sin \left(\mathrm{k}_{2 \mathrm{x}} \mathrm{x}+\mathrm{k}_{2 \mathrm{y}} \mathrm{y}-\omega_{2} \mathrm{t}\right)\), entonces los frentes de onda de las ondas coincidirán a través de la discontinuidad para siempre solo si\(\omega_{1}=\omega_{2} \equiv \omega \text { and } \mathrm{k}_{1 \mathrm{y}}=\mathrm{k}_{2 \mathrm{y}} \equiv \mathrm{k}_{\mathrm{y}}\). Ya estamos familiarizados con la primera condición del problema unidimensional, por lo que el único ingrediente nuevo es la constancia del componente y del vector de onda.

En dos dimensiones el momento es un vector:\(\boldsymbol{\Pi}=\mathrm{mu} \text { when }|\mathbf{u}| \ll \mathrm{c}\), donde u es la velocidad de la partícula. Además, la energía cinética es\(K=m|\mathbf{u}|^{2} / 2=|\mathbf{\Pi}|^{2} /(2 m)=\left(\Pi_{x}{ }^{2}+\Pi_{y}{ }^{2}\right) /(2 m)\). La relación entre la energía cinética, potencial y total no ha cambiado desde el caso unidimensional, por lo que tenemos

\[E=U+\left(\Pi_{x}^{2}+\Pi_{y}^{2}\right) /(2 m)=\text { constant. }\label{8.25}\]

La relación de Broglie nos dice eso\(\boldsymbol{\Pi}=\hbar \mathbf{k}\), así la constancia de\(\mathrm{k}_{\mathrm{y}}\) través de la discontinuidad en U nos dice que

\[\Pi_{y}=\text { constant }\label{8.26}\]

ahí

Figura 8.3: Trayectoria de un paquete de ondas a través de una energía potencial variable, U (x), que disminuye hacia la derecha.

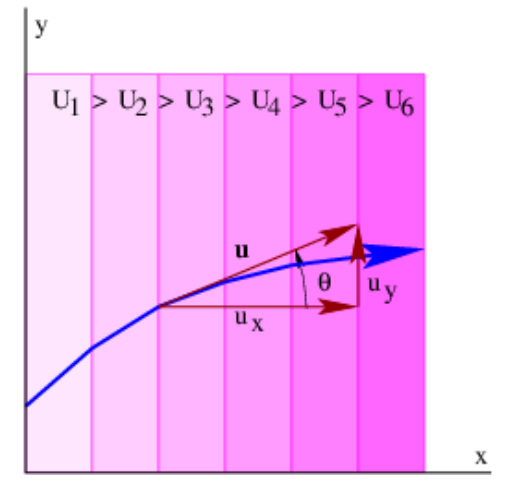
Ahora aproximemos una U (x) continuamente variable por una serie de pasos de U constante orientados normales al eje x. El análisis anterior se puede aplicar en los saltos o discontinuidades en U entre pasos, como se ilustra en la figura 8.3, con el resultado de que las ecuaciones (\ ref {8.25}) y (\ ref {8.26}) son válidas en todas las discontinuidades. Si ahora dejamos que el ancho del paso vaya a cero, estas ecuaciones entonces se vuelven válidas para U continuamente variable en x.

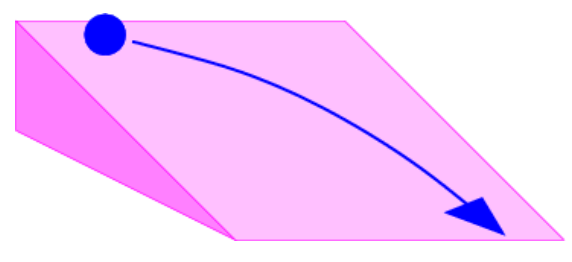
Un ejemplo de la mecánica clásica de un problema de este tipo es una bola rodando por una rampa inclinada con un componente de velocidad inicial a través de la rampa, como se ilustra en la figura 8.4. La energía potencial disminuye en la dirección de la rampa descendente, lo que resulta en una fuerza hacia abajo de la rampa. Esto acelera la pelota en esa dirección, pero deja sin cambios el componente de impulso a través de la rampa.

Figura 8.4: Ejemplo de mecánica clásica del problema ilustrado en la figura 8.3.

Usando el procedimiento que invocamos antes, encontramos los componentes de fuerza asociados a U (x) en las direcciones x e y para ser\(F_{x}=-d U / d x \text { and } F_{y}=0\). Esto generaliza a

\[\mathbf{F}=-\left(\frac{\partial U}{\partial x}, \frac{\partial U}{\partial y}, \frac{\partial U}{\partial z}\right) \quad \text { (3-D conservative force) }\label{8.27}\]

en el caso tridimensional donde la orientación de las superficies U constantes es arbitraria. También es válido cuando U (x, y, z) no se limita a una simple forma de rampa, sino que adquiere una estructura completamente arbitraria.

Las definiciones de trabajo y poder son ligeramente diferentes en dos y tres dimensiones. En particular, el trabajo se define como

\[W=\mathbf{F} \cdot \Delta \mathbf{x}\label{8.28}\]

donde Δ x es ahora un desplazamiento vectorial. El carácter vectorial de esta expresión produce una posibilidad adicional sobre el caso unidimensional, donde el trabajo es positivo o negativo dependiendo de la dirección de Δ x con relación a F. Si la fuerza y el desplazamiento del objeto sobre el que actúa la fuerza son perpendiculares entre sí, el trabajo realizado por la fuerza es en realidad cero, aunque tanto la fuerza como el desplazamiento tengan magnitudes distintas de cero. El poder exhibe un cambio similar:

\[P=\mathbf{F} \cdot \mathbf{u}\label{8.29}\]

Así, la potencia es cero si la velocidad de un objeto es normal a la fuerza que se ejerce sobre él.

Como en el caso unidimensional, el trabajo total realizado sobre una partícula equivale al cambio en la energía cinética de la partícula. Además, el trabajo realizado por una fuerza conservadora equivale a menos el cambio en la energía potencial asociada.

La conservación de energía por sí misma es algo menos útil para resolver problemas en dos y tres dimensiones que en una dimensión. Esto se debe a que conocer la energía cinética en algún momento nos dice solo la magnitud de la velocidad, no su dirección. Si la conservación de la energía no nos da la información que necesitamos, entonces debemos volver a la segunda ley de Newton, como hicimos en el caso unidimensional. Por ejemplo, si un objeto de masa m tiene velocidad inicial\(\mathbf{u}_{0}=\left(\mathrm{u}_{0}, 0\right)\) en la ubicación\((x, z)=(0, h)\) y tiene la energía potencial gravitacional\(\mathrm{U}=\mathrm{mgz}\), entonces la fuerza sobre el objeto es\(\mathbf{F}=(0,-\mathrm{mg})\). La aceleración es por lo tanto\(\mathbf{a}=\mathbf{F} / \mathrm{m}=(0,-\mathrm{g})\). Dado que\(\mathbf{a}=\mathrm{d} \mathbf{u} / \mathrm{dt}=\mathrm{d}^{2} \mathbf{x} / \mathrm{dt}^{2}\) dónde\(\mathbf{x}=(\mathrm{x}, \mathrm{z})\) está la posición del objeto, encontramos que

\[\mathbf{u}=\left(C_{1},-g t+C_{2}\right) \quad \mathbf{x}=\left(C_{1} t+C_{3},-g t^{2} / 2+C_{2} t+C_{4}\right)\label{8.30}\]

donde C ₁, C ₂, C ₃ y C ₄ son constantes a evaluar para que la solución se reduzca a las condiciones iniciales a t = 0. Las condiciones iniciales especificadas nos indican que C ₁ = u ₀, C ₂ = 0, C ₃ = 0 y C ₄ = h en este caso. A partir de estos resultados podemos inferir la posición y velocidad del objeto en cualquier momento.